中科大-凸优化 笔记(lec7)-保凸变换(上)
全部笔记的汇总贴(视频也有传送门):中科大-凸优化
{ x ∣ x ≤ 0 } \{x|x\le0\} { x∣x≤0}是凸集,是多面体 x 0 = 0 , x 1 = − ∞ x_0=0,x_1=-\infty x0=0,x1=−∞是单纯形
S + n n = 2 S + n = { ( x t y z ) ∣ x ≥ 0 , z ≥ 0 , x z ≥ y 2 } S_+^n\;\;n=2 \;\; S_+^n=\{\begin{pmatrix} x & t \\ y & z \end{pmatrix}\Big|x\ge0,z\ge0,xz\ge y^2\} S+nn=2S+n={ (xytz)∣∣∣x≥0,z≥0,xz≥y2}
一、交集
若 S 1 , S 2 S_1,S_2 S1,S2为凸集,则 S 1 ∩ S 2 S_1\cap S_2 S1∩S2为凸集。

推广 ⇒ \Rightarrow ⇒若 S a S_a Sa为凸集, ∀ a ∈ A \forall a\in A ∀a∈A,则 ∩ a ∈ A S a \cap_{a\in A}S_a ∩a∈ASa为凸集。
二、仿射函数(线性映射)
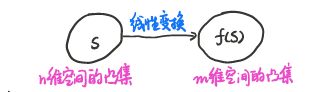
仿射函数 f : R n → R m f:\R^n\rightarrow\R^m f:Rn→Rm是仿射的,当 f ( x ) = A x + b , A ∈ R n ∗ m , b ∈ R m f(x)=Ax+b,A\in\R^{n*m},b\in\R^m f(x)=Ax+b,A∈Rn∗m,b∈Rm
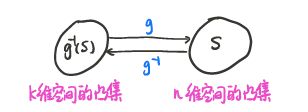
若 S ∈ R n S\in\R^n S∈Rn为凸集, f : R n → R m f:\R^n\rightarrow\R^m f:Rn→Rm是仿射的,则 f ( S ) = { f ( x ) ∣ x ∈ S } f(S)=\{f(x)|x\in S\} f(S)={ f(x)∣x∈S}为凸集。
g : R k → R n g:\R^k\rightarrow\R^n g:Rk→Rn为仿射, g − 1 ( S ) = { x ∣ f ( x ) ∈ S } g^{-1}(S)=\{x|f(x)\in S\} g−1(S)={ x∣f(x)∈S}
三、缩放和位移
缩放和移位是保持集合凸性的。
α S = { α x ∣ x ∈ S } S + a = { x + a ∣ x ∈ S } \alpha S=\{\alpha x|x\in S\}\\S+a=\{x+a|x\in S\} αS={ αx∣x∈S}S+a={ x+a∣x∈S}
四、凸集的和
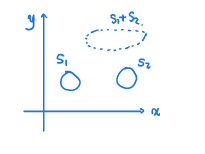
凸集的和是凸集。
S 1 + S 2 = { x + y ∣ x ∈ S 1 , y ∈ S 2 } S 1 ∗ S 2 = { x ∗ y ∣ x ∈ S 1 , y ∈ S 2 } f ( ( x , y ) ) = x + y S_1+S_2=\{x+y|x\in S_1,y\in S_2\}\\S_1*S_2=\{x*y|x\in S_1,y\in S_2\}\\f((x,y))=x+y S1+S2={ x+y∣x∈S1,y∈S2}S1∗S2={ x∗y∣x∈S1,y∈S2}f((x,y))=x+y
五、线性矩阵不等式(LMT)
A ( x ) = x 1 A 1 + ⋯ + x n A n ⪯ B , B , A i , x i ∈ S m ( A ( x ) − B ) ⪯ 0 半 负 定 A(x)=x_1A_1+\cdots+x_nA_n\preceq B,\;\;\;\;B,A_i,x_i\in S^m\\(A(x)-B)\preceq0\;\;半负定 A(x)=x1A1+⋯+xnAn⪯B,B,Ai,xi∈Sm(A(x)−B)⪯0半负定
{ x ∣ A ( x ) ⪯ B } 为 凸 集 \{x|A(x)\preceq B\}为凸集 { x∣A(x)⪯B}为凸集
证明:
定义仿射变换 f ( x ) = Δ B − A ( x ) f(x)\overset{\Delta}{=}B-A(x) f(x)=ΔB−A(x)
S + n S_+^n S+n为凸集
f − 1 ( S + n ) = { x ∣ B − A ( x ) ≥ 0 } {\color{blue}f^{-1}(S_+^n)=\{x|B-A(x)\ge0\}} f−1(S+n)={ x∣B−A(x)≥0}想象成 ∣ x ∣ |x| ∣x∣的标量
这里蓝色标注的部分有点难理解,我讲一下自己的一些看法,
-
首先,第二大点中的这个式子应该没什么问题吧。
g : R k → R n g:\R^k\rightarrow\R^n g:Rk→Rn为仿射, g − 1 ( S ) = { x ∣ f ( x ) ∈ S } g^{-1}(S)=\{x|f(x)\in S\} g−1(S)={ x∣f(x)∈S} -
然后 S + n S_+^n S+n是一个半正定矩阵,是一个凸集,所以 B − A ( x ) ∈ S + n B-A(x)\in S_+^n B−A(x)∈S+n
-
我们把 B − A ( x ) B-A(x) B−A(x)看作 f ( x ) f(x) f(x), S + n S_+^n S+n看作 S S S,可以得到 g − 1 ( S + n ) = { x ∣ B − A ( x ) ∈ S + n } g^{-1}(S_+^n)=\{x|B-A(x)\in S_+^n\} g−1(S+n)={ x∣B−A(x)∈S+n}
下一章传送门:中科大-凸优化 笔记(lec8)-保凸变换(下)