sklearn机器学习：岭回归Ridge

在sklearn中，岭回归由线性模型库中的Ridge类来调用：

Ridge类的格式

sklearn.linear_model.Ridge (alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=’auto’, random_state=None)
和线性回归相比，岭回归的参数稍微多了那么一点，但是真正核心的参数就是正则项系数$\alpha$，其他参数是希望使用最小二乘法之外的求解方法求解岭回归的时候才需要的，通常完全不会去用这些参数。所以，只需了解$\alpha$的用法即可。
之前的博文《sklearn机器学习:线性回归LinearRegression》中，在加利佛尼亚房屋价值数据集上使用线性回归，得出的结果大概是训练集上的拟合程度是60%，测试集上的拟合程度也是60%左右，这个很低的拟合程度是不是由多重共线性造成的呢？统计学会通过VIF(方差膨胀因子)或者各种检验来判断数据是否存在共线性，而在机器器学习中，可以使用模型来判断——如果一个数据集在岭回归中使用各种正则化参数取值下，模型表现没有明显上升（比如出现持平或者下降），则说明数据没有多重共线性，顶多是特征之间有一些相关性。反之，如果一个数据集在岭回归的各种正则化参数取值下，表现出明显的上升趋势，则说明数据存在多重共线性。
接下来，用加利佛尼亚房屋价值数据集验证一下：

#岭回归验证
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression, Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt
housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
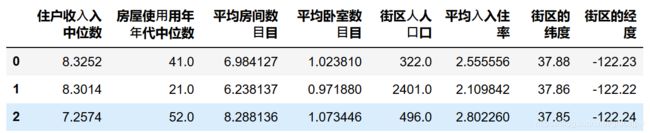
X.columns = ["住户收⼊入中位数","房屋使⽤用年年代中位数","平均房间数⽬目"
,"平均卧室数⽬目","街区⼈人⼝口","平均⼊入住率","街区的纬度","街区的经度"]
X.head(3)

#划分数据集
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#数据集索引恢复
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])
#使用岭回归建模
reg = Ridge(alpha=1).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)

0.6043610352312276

#交叉验证下，与线性回归相比，岭回归的结果如何变化？
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()

#细化一下学习曲线
alpharange = np.arange(1,201,10)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
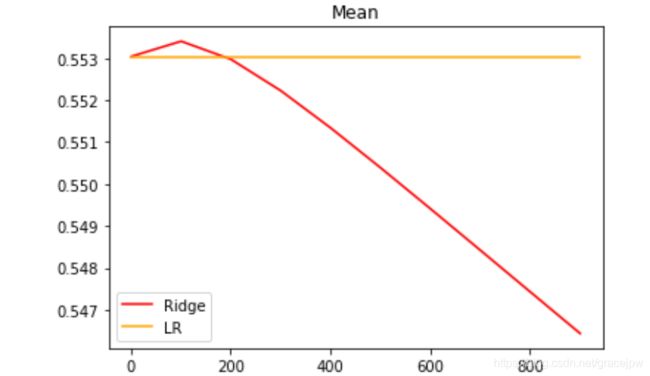
plt.title("Mean")
plt.legend()
plt.show()

可见，加利佛尼亚数据集上，岭回归的结果轻微上升，随后骤降。可以说，加利利尼亚房屋价值数据集带有很轻微的一部分共线性，这种共线性被正则化参数$\alpha$消除后，模型的效果提升了一点点，但是对于整个模型而言是杯水⻋车薪。在过了控制多重共线性的点后，模型的效果飞速下降，显然是正则化的程度太重，挤占了参数$\omega$本来的估计空间。从这个结果可以看出，加利佛尼亚数据集的核心问题不在于多重共线性，岭回归不能够提升模型表现。
另外，在正则化参数逐渐增大的过程中，可以观察一下模型的方差如何变化：

#模型方差如何变化？
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
    varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
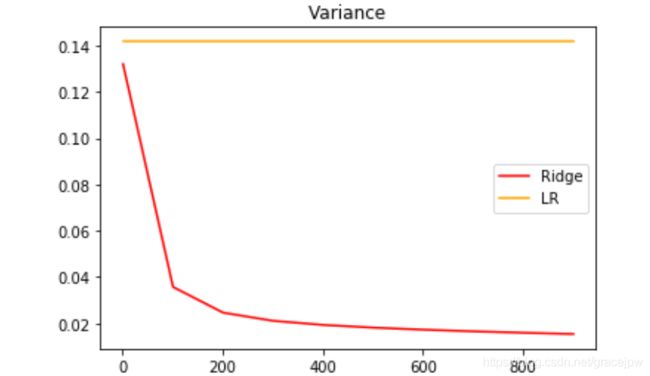
plt.title("Variance")
plt.legend()
plt.show()

可以发现，模型的方差上升快速，不过方差的值本身很小，其变化不超过R²上升部分的1/3，因此只要噪声的状况维持恒定，模型的泛化误差可能还是一定程度上降低了的。虽然岭回归和Lasso不是设计来提升模型表现，而是专注于解决多重共线性问题的，但当$\alpha$在一定范围内变动的时候，消除多重共线性也许能够一定程度上提高模型的泛化能力。
但是泛化能力毕竟没有直接衡量的指标，因此往往只能通过观察模型的准确性指标和方差来大致评判模型的泛化能力是否提高。来看看多重共线性更为明显一些的情况：

from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
X = load_boston().data
y = load_boston().target
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#先查看⽅方差的变化
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
    varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()

#查看R2的变化
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
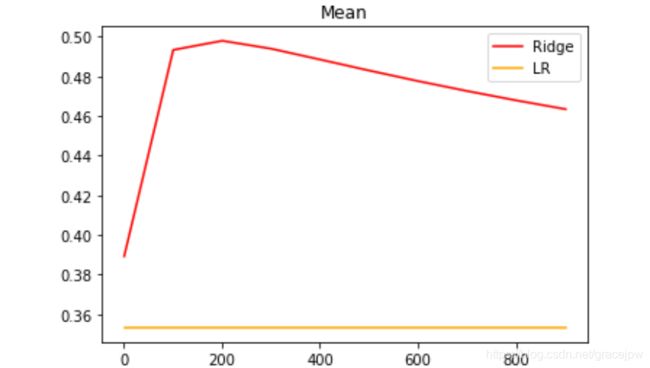
plt.title("Mean")
plt.legend()
plt.show()

#细化学习曲线
alpharange = np.arange(100,300,10)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    #linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    #linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
#plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

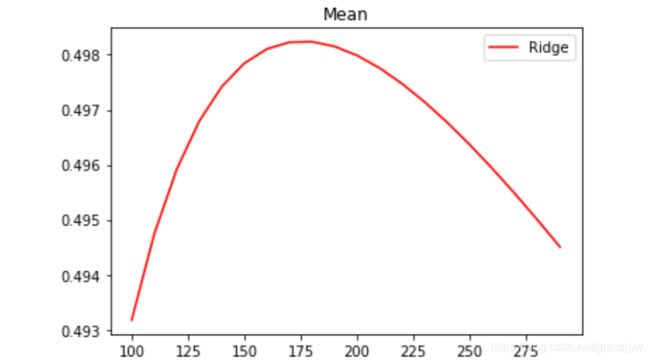
可以发现，比起加利佛尼亚房屋价值数据集，波士顿房价数据集的方差降低明显，偏差也降低明显，可见使用岭回归还是起到了一定的作用，模型的泛化能力是有可能会上升的。
遗憾的是，没有人会希望自己获取的数据中存在多重共线性，因此发布到scikit-learn或者kaggle上的数据基本都经过一定的多重共线性的处理，要找出绝对具有多重共线性的数据非常困难，也就无法给大家展示岭回归在实际数据中大显身手的模样。也许可以找出具有一些相关性的数据，但是如果
去尝试就会发现，基本上如果使用岭回归或者Lasso，模型的效果都是会降低，很难升高，这恐怕也是岭回归和Lasso一定程度上被机器器学习领域冷遇的原因。