《机器学习实战：基于Scikit-Learn、Keras和TensorFlow》第二版中文解读第十章

标题基于keras的人工神经网络的介绍

---

前言

鸟儿启发我们飞翔，牛蒡激发了魔术贴的灵感，大自然激发了无数的发明。因此，通过观察大脑的结构来获得如何建造智能机器的灵感似乎是合乎逻辑的。这就是引发人工神经网络(ANNs)的逻辑:ANN是由我们大脑中发现的生物神经元网络所激发而组成的机器学习模式。然而，尽管飞机的灵感来自鸟类，但它们不需要扇动翅膀。同样地，ann也逐渐变得与它们的表亲(人类大脑神经元)截然不同。一些研究人员甚至认为我们应该完全放弃生物学上的类比(例如，用“单元”而不是“神经元”)，以免我们把创造力限制在生物学上可行的系统上. ANNs是深度学习的核心。它们是多用途的、强大的和可扩展的，这些因素使它们成为处理大型和高度复杂的机器的理想工具学习任务，如分类数十亿的图像(如谷歌图像)，支持语音识别服务(如苹果的Siri)，每天向数亿用户推荐最好的视频(如YouTube)，或学习在围棋比赛中击败世界冠军(如DeepMind的)AlphaGo。 本章的第一部分介绍了人工神经网络，首先快速浏览了最早的神经网络架构，最后介绍了多层神经网络感知器(**MLPs**)，目前被大量使用(其他架构将在下一章探讨).在第二部分中，我们将了解如何使用流行的**Keras API**实现神经网络。这是一个设计精美、简单的高级API，用于构建、培训、评估和运行神经网络。但是不要被它的简单所迷惑:它的表现力和灵活性足以让您构建各种各样的神经网络架构。事实上，对于您的大多数用例来说，它可能已经足够了。如果您需要额外的灵活性，您总是可以使用底层API编写定制的Keras组件，我们将在第12章中看到。但首先，让我们回到过去看看人工神经网络是如何产生的!

---

一、从生物神经元到人工神经元

令人惊讶的是，ANN已经存在很长一段时间了:它最早是由神经生理学家Warren McCulloch和数学家Walter Pitts在1943年引入的。在他们具有里程碑意义的论文《的逻辑演算》中McCulloch和Pitts提出了一个简化的计算模型，用来描述生物神经元如何在动物大脑中协同工作，利用命题逻辑进行复杂的计算。这是第一个人工神经网络架构。从那时起，许多其他的架构被发明出来，政所我们所看到那样。
ANN的早期成功让人们普遍相信，我们很快就能与真正的智能机器对话了。到了20世纪60年代，这一承诺将无法实现(至少在相当一段时间内)的事实变得明朗起来，于是资金流向了其他地方，ANNs进入了一个漫长的冬天。在20世纪80年代早期，新的结构被发明出来，更好的训练技术被开发出来，引发了对联结主义(神经网络的研究)的兴趣的复兴。但进展缓慢，到了20世纪90年代，出现了其他强大的机器学习技术，如支持向量机(见第5章)。这些技术似乎比人工神经网络提供了更好的结果和更坚实的理论基础，因此，对神经网络的研究再次被搁置。
但是目前,有几点原因使我们对神经网络的信心重燃起来:

• 大量的训练数据
• 计算能力的巨大增长(GPU)
• 训练算法的改进
• 神经网络的一些理论局限性在实践中被证明是良性的
• ANNs进入了资金和发展的良性循环

1.生物神经元

在我们讨论人工神经元之前，让我们快速看一下生物神经元(如图所示。正如我们高中生物课本上所描述的那样,它是一种外形奇特的细胞，主要存在于动物的大脑中。它是由一个包含细胞核的细胞体和细胞的大部分复杂成分，许多被称为树突的分支，加上一个非常长的延伸，被称为轴突。轴突的长度可能是细胞体的几倍，也可能是数万倍。靠近轴突的末端，轴突分裂成许多分支，这些分支的顶端是称为突触末端(或简称突触)的微小结构，它们与其他神经元的树突或细胞体相连。生物神经元产生称为动作电位(APs，简称信号)的短电脉冲，这些电脉冲沿着轴突传递，使突触释放称为神经递质的化学信号。当一个神经元在几毫秒内接收到足够数量的神经递质时,它就会发射自己的电脉冲(实际上，它取决于神经递质，因为它们中的一些可以抑制神经元的冲动)。
因此，单个的生物神经元似乎以一种相当简单的方式活动，但它们是由数十亿个巨大的网络组织起来的，每个神经元通常与数千个其他神经元相连。高度复杂的计算可以由相当简单的神经元组成的网络来完成，就像简单蚂蚁的共同努力可以形成一个复杂的蚁丘一样。生物神经网络的结构(bnn)仍然是活跃的研究课题,但大脑的某些部分被映射,和神经元似乎经常组织在连续层,尤其是在大脑皮层(即你的大脑的外层),如图所示。

2.用神经元进行逻辑计算

McCulloch和Pitts提出了一个非常简单的生物神经元模型，后来被称为人工神经元:它有一个或多个二进制(开/关)输入和一个二进制输出。当超过一定数量的输入被激活时，人工神经元就会激活它的输出。在他们的论文中，他们展示了即使有这样一个简化的模型，也可以建立一个人工神经元网络来计算任何你想要的逻辑命题。为了了解这样的网络是如何工作的，让我们构建一些执行各种逻辑计算的ANN(见图)，在这里我们假设一个神经元在至少两个输入是活跃的时候被激活。

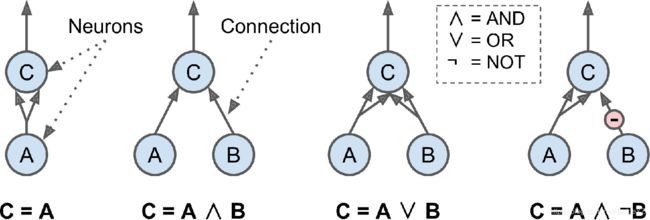
• 第一个神经元相当于恒等映射函数C=A
• 第二个神经元相当于"与".即加法,当AB同时激活时C才激活
• 第三个神经元是"或",仅需AB任意一个神经元是激活的,C就激活
• 如图所示,第四个神经元是当A为激活.B不激活时候,C才激活

3.感知机

前向计算

感知机是一种最简单的ANN,如下图所示,有三个输入x1,x2,x3,它们想要进入一个逻辑单元里必须先与其对应的权值相乘,这里分别是**(w1,w2,w3),进入逻辑单元后相加到一起,然后经过一个阶跃函数**Step Function(也成激活函数Activation Function)后,得到最终的结果

常用激活函数:有Sigmoid、tanh、relu等，在这里我们用最简单的sgn函数

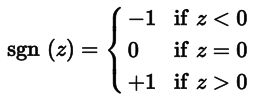
举个例子吧：
输入是x:1,2,3,对应的权值是w:1,-1,2,他们的结果相加就是1x1+2x(-1)+3x2=5,然后这个5进入了激活函数sgn,因为5>0,经过激活函数后这个逻辑单元给出的值就是1了.

上面我们使用一个逻辑单元得到一个输出,那如果我们有多个逻辑单元,有几个输出呢?答案显而易见,2个单元就有2个输出,3个就又3个,以此我们可以有很多个逻辑单元来进行我们的计算.

在这里要引入线性代数的概念了,因为我们有多个输出多个权值,把公式展开横着写估计要写很长(比如w1x2+w2x2+…+wnxn),但是我们用矩阵形式表示就会简单很多.

这里X对应的是输入矩阵,W对应的是权值矩阵,φ是激活函数,这样表示就简单很多了.

我们前面讨论了如何得出一个神经元的输出,那么只有输出我们也称不上学习呀,所以就要开始思考怎样用这个输出来影响后面的权值,逐渐调整权值来得到我们想要的完美结果.
那么感知器是如何训练的呢?Rosenblatt提出的感知器训练算法很大程度上受到了Hebbs规则的启发。在他1949年出版的《行为组织》(Wiley)一书中，Donald Hebb提出，当一个生物神经元经常触发另一个神经元时，这两个神经元之间的联系会变得更强。后来，齐格里德·洛维尔用一个朗朗上口的短语概括了赫布的观点:一起放电的细胞连接在一起;也就是说，当两个神经元同时放电时，它们之间的连接重量会增加。这个规则后来被称为赫伯规则(或赫伯学习)。感知器是用这个规则的一个变体来训练的，它考虑到网络在做预测时所犯的错误;感知器学习规则加强了有助于减少错误的联系。更具体地说，感知器每次输入一个训练实例，然后对每个实例进行预测。对于每一个产生错误预测的输出神经元，它都会加强来自输入的连接权重，而这些连接权重本来会有助于做出正确的预测。如公式所示

• wi,j是神经元i和神经元j之间的连接权值
• xi是第i个输入单元的当前输入值
• yi是完美的输出值
• ŷi是经过当前这个单元得到的输出值
• η是学习率

我们进行学习的过程中,权值w是会根据我们的输入输出情况来调整的,如果我们的理想输出和实际输出的差值较大,w的调整大小也会较大.如果实际输出大了,w就要相应减小一点,这就是一个学习的过程.
多说无益,我们代码实战

import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron #导入sklearn里面的感知机单元类
iris = load_iris()
X = iris.data[:, (2, 3)] # petal length, petal width
y = (iris.target == 0).astype(np.int) # Iris setosa?
per_clf = Perceptron()
per_clf.fit(X, y)
y_pred = per_clf.predict([[2, 0.5]])

4.多层感知机

有机器学习的知识小伙伴可能意识到,这不就是和梯度下降差不多吗,实际上sklearn的Perceptron等于SGDClassifier(loss=“perceptron”,learning_rate=“constant”, eta0=1,penalty=None).在简单问题上其实用逻辑回归更好,感知机是一个基于硬阈值的预测,一但你没达到那个阈值可能这个神经元就会把值给变成0,就啥都没有了.但是在复杂问题上,逻辑回归可能并不那么准确,我们又把目光放到了感知机上,其实感知机的层层堆叠形成所谓的多层感知机就可以处理很多复杂问题了.

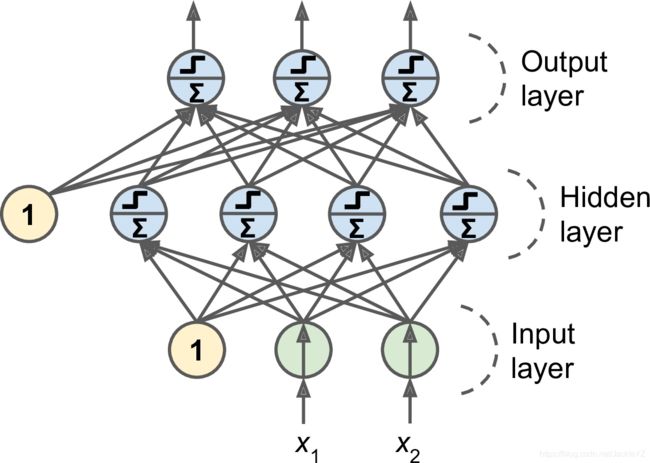
如图所示,就是我们上面所描述的多个单元堆积起来的一个多层感知机MLP(Multilayer Perceptron),最上面是输出层,最下面的是输入层,而中间的我们通常称为隐层.1是我们的bias.

反向传播

1986年，David Rumelhart, Geoffrey Hinton和Ronald Williams发表了一篇开创性的论文，介绍了反向传播训练算法，这种算法至今仍在使用。简而言之，就是梯度下降使用一种有效的自动计算梯度的技术:在仅仅通过网络的两次(一个向前，一个向后)，反向传播算法能够计算梯度的网络的误差对每一个单一的模型参数进行更新.
这个算法非常重要总的来说就是:对于每个训练实例，反向传播算法首先做一个预测(前向传递)并测量错误，然后反向通过每一层来测量来自每个连接的错误贡献(反向传递)，最后调整连接权重以减少错误(梯度下降)。想要了解详细内容推荐吴恩达老师的视频,讲的十分详细.
在MLP中我们不能再继续沿用上面那个简单的sgn激活函数,因为这个会导致梯度消失的问题,在这里我们采用sigmoid函数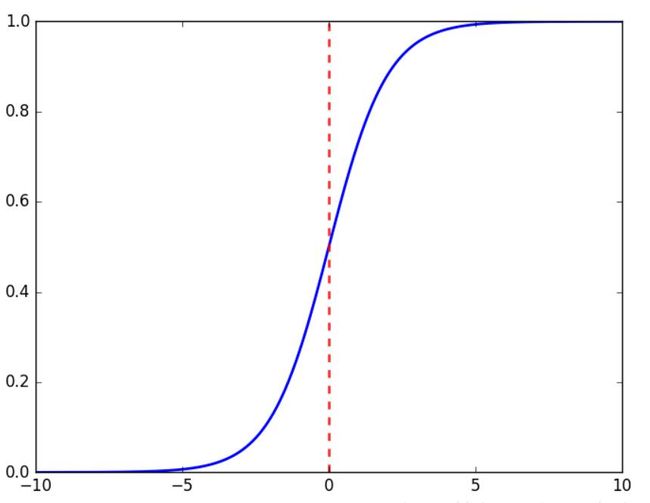
是不是看上去比较平滑,在0的邻域就可以很大程度避免梯度消失,还有其他激活函数也可以使用,比如relu函数虽然在0会有一个阶跃的梯度,但是它用来计算是十分快速的.
那么问题来了,我们为什么需要激活函数在我们的MLP中呢?
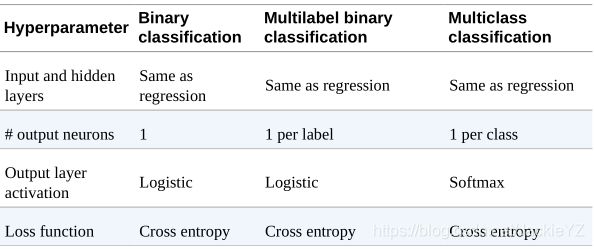
原因很简单,如果我们不用激活函数,无论你堆叠多少层,多深的网络,最终的计算也只是简单的线性计算,并没有像生物神经元那样有一个"激活"的作用.而在最后一层,我们通常是得到我们的输出结果,如果继续用sigmod函数就没有这么直观可以表达我们的输出,所以一般在线性任务中我们最后的输出层可以用一个Logistic激活,在多分类任务中我们可以用Softmax.而在反向传播中我们是通过一个LOSS function损失函数来计算我们的梯度

二、用Keras实现MLPs

1.安装

可以进入tf的官网按照对应的系统进行安装,这里就略过https://www.tensorflow.org/install/
这里给出keras的中文文档
https://keras.io/zh/
安装完毕后在IDLE上输入代码可以查看是否安装成功

>>> import tensorflow as tf
>>> from tensorflow import keras
>>> tf.__version__
'2.0.0'
>>> keras.__version__
'2.2.4-tf'

2.利用Sequential API来构建一个图像分类器

1).导入数据

fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()

这里用可keras的datasets来导入fashion_mnist数据,详情可以查看keras文档,还有很多练手数据可以导入

>>> X_train_full.shape
(60000, 28, 28)
>>> X_train_full.dtype
dtype('uint8')

训练数据有6W张 28x28像素大小的图片,编码是uint8编码
与以往机器学习的步骤一样,需要划分验证集:

X_valid, X_train = X_train_full[:5000] / 255.0, X_train_full[5000:] /
255.0
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]

这里/255.0是为了把原始像素(0-255)变成(0-1)的范围内方便我们的激活函数工作.
由于Fashion MNIST有十个类别,而且分别是用数字表示,比如1代表T-shirt,所以我们要构建一个列表来方便表示标签

class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]

例如训练集的第一张图片标签为

>>> class_names[y_train[0]]
'Coat'

2).构建模型

现在我们可以开始构建一个MLP了!!!

model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))

只需要实例化Sequential,然后在后面运用add方法来顺序增加我们的层就行了.这里第一层是Flatten层,就是把我们的28x28的矩阵给变成一个一维的数组里面含有784个元素,后面三个是Dense层,并有相应的激活函数,正如上面所说,多分类任务最后一层采用softmax函数,而且有多少个标签就有多少个神经元(这里是十个)
也可以采用以下形式:

model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="relu"),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax")
])

这两种方法构建model是等效的
接下来我们看一下我们的网络构成

>>> model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 300) 235500
_________________________________________________________________
dense_1 (Dense) (None, 100) 30100
_________________________________________________________________
dense_2 (Dense) (None, 10) 1010
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0

3).编译模型

model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])

loss是损失函数,由于是多分类任务这里我们用交叉熵损失函数,用随机梯度下降的方法来进行优化

---

### 4).训练模型

>>> history = model.fit(X_train, y_train, epochs=30,
... validation_data=(X_valid, y_valid))
...
Train on 55000 samples, validate on 5000 samples
Epoch 1/30
55000/55000 [======] - 3s 49us/sample - loss: 0.7218 - accuracy:0.7660
- val_loss: 0.4973 - val_accuracy:0.8366
Epoch 2/30
55000/55000 [======] - 2s 45us/sample - loss: 0.4840 - accuracy:0.8327
- val_loss: 0.4456 - val_accuracy:0.8480
.........
Epoch 30/30
55000/55000 [======] - 3s 53us/sample - loss: 0.2252 - accuracy:0.9192 
-val_loss: 0.2999 - val_accuracy:0.8926

我们可以看到训练了50个周期以后,模型在训练数据上的准确率接近92%,在测试集上是89%.

5).观察模型

fit()方法返回一个包含训练参数的历史对象
(history.params)，它所经历的epoch列表(history.epoch)，最重要的是一个字典(history.history)，其中包含它在训练集和验证集(如果有的话)上的每个epoch结束时测量的损失和额外度量。如果使用这个字典创建一个pandas DataFrame并调用它的plot()方法，就会得到如图所示的学习曲线

import pandas as pd
import matplotlib.pyplot as plt
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1) # set the vertical range to [0-1]
plt.show()

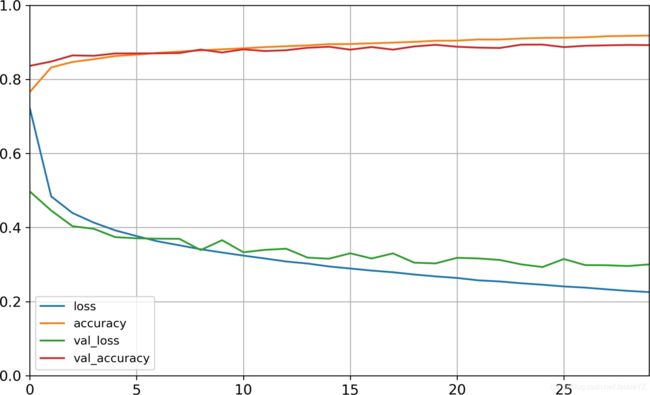
可以看到我们的训练精度和验证精度都在上升,而loss都是下降的
如果对结果不满意,我们可以返回去调整我们的超参数:学习率,单元个数,激活函数,或者batch_size

6).利用模型去预测

>>> X_new = X_test[:3]
>>> y_proba = model.predict(X_new)
>>> y_proba.round(2)
array([[0. , 0. , 0. , 0. , 0. , 0.03, 0. , 0.01, 0. , 0.96],
[0. , 0. , 0.98, 0. , 0.02, 0. , 0. , 0. , 0. , 0. ],
[0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]],
dtype=float32)

可以看出,经过我们的softmax层,得到的输出结果是加起来等于1的,比如第一个预测,模型预测这个物品最大可能是第九类ankle boot,概率为96%,而只有3%的可能是第五类sandal,1%的可能是第七类sneaker
如果只是关心得分最高的类,可以:

>>> y_pred = model.predict_classes(X_new)
>>> y_pred
array([9, 2, 1])
>>> np.array(class_names)[y_pred]
array(['Ankle boot', 'Pullover', 'Trouser'], dtype=')
>>> y_new = y_test[:3]
>>> y_new
array([9, 2, 1])

3.利用Sequential API来构建一个回归模型

1).简易回归模型

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#导入数据
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)

#构建模型
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu",
input_shape=X_train.shape[1:]),
keras.layers.Dense(1)
])
#编译模型
model.compile(loss="mean_squared_error", optimizer="sgd")
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3] # pretend these are new instances
y_pred = model.predict(X_new)

如上所示,用Sequential来构建一个model是非常简便的

2).复杂回归模型

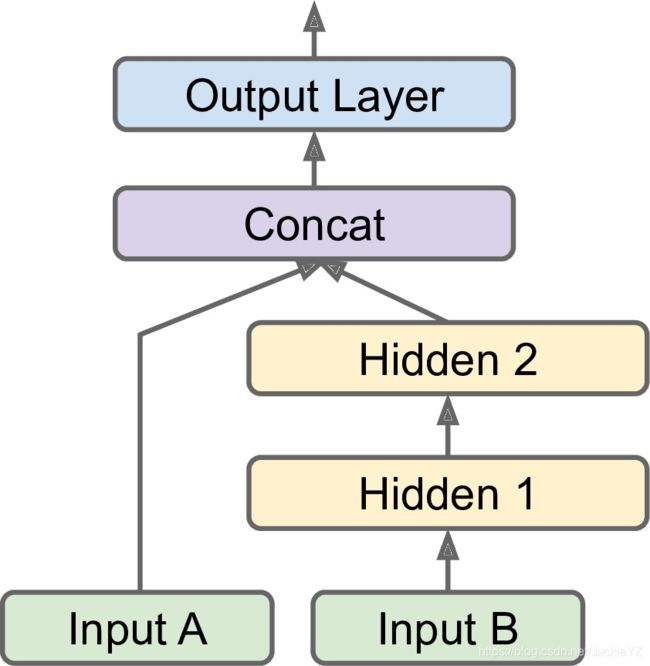
在网络中不仅有层层递进的结构,也有将输入直接接到后面输出的网络结构

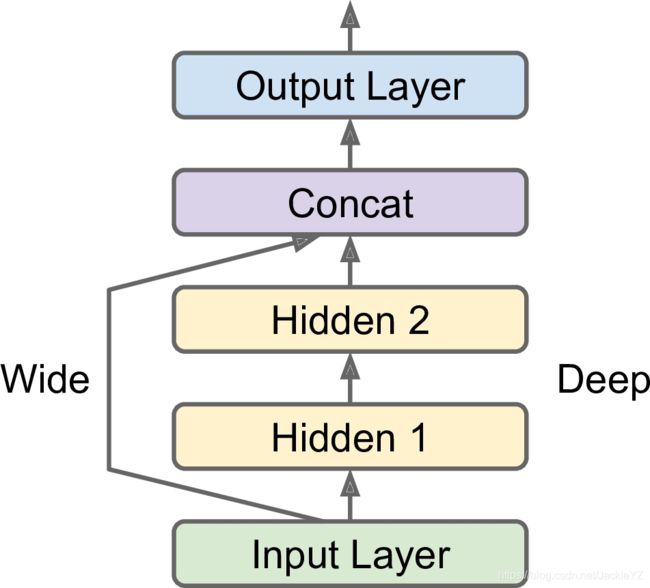
我们可以这样构造

input_ = keras.layers.Input(shape=X_train.shape[1:])
hidden1 = keras.layers.Dense(30, activation="relu")(input_)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.Concatenate()([input_, hidden2])
output = keras.layers.Dense(1)(concat)
model = keras.Model(inputs=[input_], outputs=[output])

• 首先，我们需要创建一个输入对象。这是模型将获得的输入类型的规范，包括它的形状和dtype,一个模型实际上可能有多个输入，我们很快就会看到。
• 接下来，我们使用ReLU激活函数创建一个包含30个神经元的密集层。一旦它被创建，请注意，我们像调用函数一样调用它，将输入传递给它。这就是为什么这叫做功能性API。请注意，我们只是告诉Keras应该如何将各层连接在一起;目前还没有处理实际数据
• 然后我们创建第二个隐藏层，并再次使用它作为一个函数。注意，我们将第一个隐藏层的输出传递给它。
• 接下来，我们创建一个连接层，并且再次将其作为函数使用，以连接第二层隐藏层的输入和输出。您可能更喜欢使用keras .layers. Concatenate()函数，该函数创建一个连接层，并立即使用给定的输入调用该层。
• 然后我们创建输出层，其中只有一个神经元，没有激活函数，我们像调用函数一样调用它，将连接的结果传递给它。
• 最后，我们创建一个Keras模型，指定使用哪些输入和输出。

一旦构建了Keras模型，一切就与前面完全一样了，因此不需要在这里重复:必须编译模型、训练它、评估它，并使用它来进行预测。

以下列举另外几种变形以及代码:
双输入:

input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="output")(concat)
model = keras.Model(inputs=[input_A, input_B], outputs=[output])

双输入双输出:

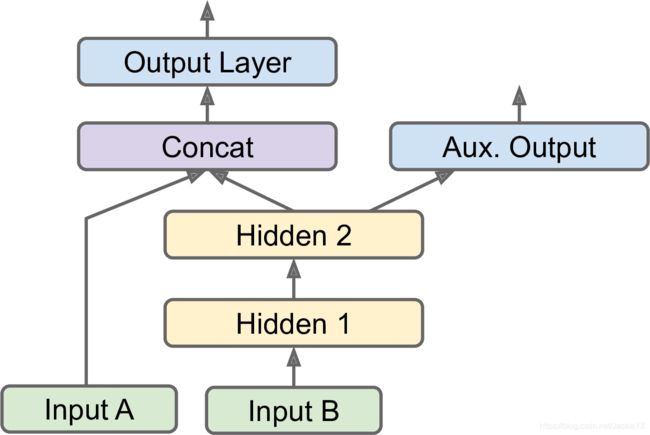
input_A = keras.layers.Input(shape=[5], name="wide_input")
input_B = keras.layers.Input(shape=[6], name="deep_input")
hidden1 = keras.layers.Dense(30, activation="relu")(input_B)
hidden2 = keras.layers.Dense(30, activation="relu")(hidden1)
concat = keras.layers.concatenate([input_A, hidden2])
output = keras.layers.Dense(1, name="main_output")(concat)
aux_output = keras.layers.Dense(1, name="aux_output")(hidden2)
model = keras.Model(inputs=[input_A, input_B], outputs=[output,
aux_output])

在这里要注意,两个输出对应两个损失函数,如果我们只定义一个,Keras将假设所有输出必须使用相同的损失。默认情况下，Keras将计算所有这些损失，并简单地将它们相加，得到用于训练的最终损失。
所以我们可以传递一个loss列表:

model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1],
optimizer="sgd")

同样的,我们想要两个输出都作用在预测标签上,就要传递标签列表给它,valid也是一样:

history = model.fit(
[X_train_A, X_train_B], [y_train, y_train], epochs=20,
validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid]))

预测也同样要返回列表:

y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B])

4.利用子类化来构建模型

通过重写父类keras.Model来构建一个模型
在**init里定义模型的层和参数
在call()**里定义你所想要的模型走向,可以天马行空定义各种for,while语句,极大增加了模型的灵活性

class WideAndDeepModel(keras.Model):
	def __init__(self, units=30, activation="relu", **kwargs):
		super().__init__(**kwargs) # handles standard args (e.g., name)
		self.hidden1 = keras.layers.Dense(units, activation=activation)
		self.hidden2 = keras.layers.Dense(units, activation=activation)
		self.main_output = keras.layers.Dense(1)
		self.aux_output = keras.layers.Dense(1)
	def call(self, inputs):
		input_A, input_B = inputs
		hidden1 = self.hidden1(input_B)
		hidden2 = self.hidden2(hidden1)
		concat = keras.layers.concatenate([input_A, hidden2])
		main_output = self.main_output(concat)
		aux_output = self.aux_output(hidden2)
		return main_output, aux_output
model = WideAndDeepModel()

但是运用这种方法有个缺点,在用summary()时候并不能完整打印你的完整模型顺序序列,只能打印__init__里面定义的层,因为这个call方法是当模型运作起来才会实现,所以除非你需要灵活性,否则用Sequential是一个不错的选择.

5.保存模型

当使用顺序API或函数API时，保存训练好的Keras模型非常简单:

model = keras.layers.Sequential([...]) # or keras.Model([...])
model.compile([...])
model.fit([...])
model.save("my_keras_model.h5")

加载模型:

model = keras.models.load_model("my_keras_model.h5")

如果只想保存权重可以用save_weights和load_weights方法

6.运用回调函数callback

fit()方法接受一个callbacks参数，该参数允许您指定Keras将在训练开始和结束、每个epoch开始和结束、甚至在处理每个批处理之前和之后调用的对象列表。例如ModelCheckpoint回调在训练期间定期保存模型的检查点，默认在每个epoch结束时保存:

checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5")
history = model.fit(X_train, y_train, epochs=10, callbacks=[checkpoint_cb])

此外，如果您在训练期间使用验证集，您可以在创建ModelCheckpoint时设置save_best_only=True。在这种情况下，它只会在模型在验证集上的性能达到最佳时保存模型。这种方式,你不需要担心培训太久和过度拟合训练集因为这样可以简单地恢复过去训练好的模型,这将是最好的模型验证集。
下面的代码是一个简单的方法来实现早期停止:

checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5",
save_best_only=True)
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb])
model = keras.models.load_model("my_keras_model.h5") 
# roll back to best model

另一种实现早期停止的方法是简单地使用earlystop回调。当在多个epoch(由patience参数定义)上测量验证集没有进展时，它将中断训练，并且可以选择回滚到最佳模型。你可以结合这两种回调来节省你的模型的检查点(以防你的电脑崩溃)，并在没有更多进展的时候中断训练(避免浪费时间和资源):

early_stopping_cb = keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb])

也可以通过重写callback来实现你想要的功能,例如在训练期间打印验证损失和训练损失的比值:

class PrintValTrainRatioCallback(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
print("\nval/train: {:.2f}".format(logs["val_loss"] /
logs["loss"]))

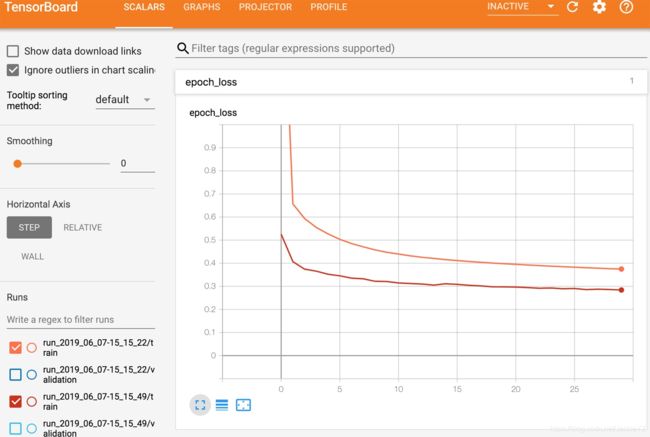
7.利用tensorbroad实现可视化

TensorBoard是一个伟大的交互式可视化工具,您可以使用它来查看训练期间学习曲线,比较学习曲线之间的关系,可视化计算图表,分析训练数据,视图生成的图像模型,可视化复杂多维数据投影到3d和自动聚集,和更多!
当您安装TensorFlow时，该工具会自动安装，所以您已经拥有它了。

让我们从定义用于TensorBoard日志的根日志目录开始，加上一个小函数，该函数将根据当前日期和时间生成子目录路径，以便在每次运行时都有所不同。您可能希望在日志目录名中包含额外的信息，例如您正在测试的超参数值，以便更容易地了解您正在查看的内容

import os
root_logdir = os.path.join(os.curdir, "my_logs")
def get_run_logdir():
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir() # e.g., './my_logs/run_2019_06_07-15_15_22'

[...] # Build and compile your model
tensorboard_cb = keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid),
callbacks=[tensorboard_cb])

打开命令提示行,输入

tensorboard --logdir=./my_logs --port=6006

然后把得到的网址复制到浏览器打开即可

三.微调神经网络超参数

想要自动寻找最优参数的办法之一是通过Scikit-Learn API 的封装器,然后用RandomizedSearchCV来搜索

构建一个建造模型的函数:

def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]):
	model = keras.models.Sequential()
	model.add(keras.layers.InputLayer(input_shape=input_shape))
	for layer in range(n_hidden):
	model.add(keras.layers.Dense(n_neurons, activation="relu"))
	model.add(keras.layers.Dense(1))
	optimizer = keras.optimizers.SGD(lr=learning_rate)
	model.compile(loss="mse", optimizer=optimizer)
	return model

实例化sklearn API:
这里可以传入三种参数:

1. 一个函数；
2. 实现 call 方法的类的实例；
3. None。这意味着你实现了一个继承自 KerasClassifier 或KerasRegressor 的类。当前类 call 方法将被视为默认的

keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model)

现在我们可以像使用普通的Scikit-Learn回归变量一样使用这个对象:我们可以使用它的fit()方法对它进行训练，然后使用它的score()方法对它进行评估，并使用它的predict()方法对它进行预测，如下代码所示:

keras_reg.fit(X_train, y_train, epochs=100,
	validation_data=(X_valid, y_valid),
	callbacks=[keras.callbacks.EarlyStopping(patience=10)])
mse_test = keras_reg.score(X_test, y_test)
y_pred = keras_reg.predict(X_new)

我们不想像这样训练和评估一个单一的模型，尽管我们想训练数百个变量，看看哪个在验证集上表现最好。因为有很多超参数，最好使用随机搜索而不是网格搜索。让我们尝试探索隐藏层的数量，神经元的数量，和学习率:

from scipy.stats import reciprocal
from sklearn.model_selection import RandomizedSearchCV
param_distribs = {
     
	"n_hidden": [0, 1, 2, 3],
	"n_neurons": np.arange(1, 100),
	"learning_rate": reciprocal(3e-4, 3e-2),
}
rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10,cv=3)
rnd_search_cv.fit(X_train, y_train, epochs=100,
	validation_data=(X_valid, y_valid),
	callbacks=[keras.callbacks.EarlyStopping(patience=10)])

总结

让我们总结一下到目前为止你在这一章中学到的东西:我们看到了神经网络从何而来，MLP是什么，如何使用它进行分类和回归，以及如何使用tf。如何使用功能API或子类化API来构建更复杂的模型体系结构。您学习了如何保存和恢复模型，以及如何对检查点、早期停止等使用回调。最后，您学习了如何使用TensorBoard进行可视化。您已经可以使用神经网络来解决许多问题了!

参考书籍:《机器学习实战：基于Scikit-Learn、Keras和TensorFlow》第二版