《视觉SLAM十四讲 第二版》笔记及课后习题(第八讲)
读书笔记:视觉里程计2
直接法是视觉里程计另一主要分支,它与特征点法有很大不同。虽然它还没有成为现在VO 中的主流,但经过近几年的发展,直接法在一定程度上已经能和特征点法平分秋色。
直接法的引出
上一讲我们介绍了使用特征点估计相机运动的方法。尽管特征点法在视觉里程计中占据主流地位,研究者们认识到它至少有以下几个缺点:
- 关键点的提取与描述子的计算非常耗时。实践当中,SIFT 目前在CPU 上是无法实时计算的,而ORB 也需要近20 毫秒的计算。如果整个SLAM 以30 毫秒/帧的速度运行,那么一大半时间都花在计算特征点上。
- 使用特征点时,忽略了除特征点以外的所有信息。一张图像有几十万个像素,而特征点只有几百个。只使用特征点丢弃了大部分可能有用的图像信息。
- 相机有时会运动到特征缺失的地方,往往这些地方没有明显的纹理信息。例如,有时我们会面对一堵白墙,或者一个空荡荡的走廓。这些场景下特征点数量会明显减少,我们可能找不到足够的匹配点来计算相机运动。
我们看到使用特征点确实存在一些问题。有没有什么办法能够克服这些缺点呢?我们有以下几种思路:
• 保留特征点,但只计算关键点,不计算描述子。同时,使用光流法(Optical Flow)来跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间,但光流本身的计算需要一定时间;
• 只计算关键点,不计算描述子。同时,使用直接法(Direct Method)来计算特征点在下一时刻图像的位置。这同样可以跳过描述子的计算过程,而且直接法的计算更加简单。
• 既不计算关键点、也不计算描述子,而是根据像素灰度的差异,直接计算相机运动。
第一种方法仍然使用特征点,只是把匹配描述子替换成了光流跟踪,估计相机运动时仍使用对极几何、PnP 或ICP 算法。而在后两个方法中,我们会根据图像的像素灰度信息来计算相机运动,它们都称为直接法。
使用特征点法估计相机运动时,我们把特征点看作固定在三维空间的不动点。根据它们在相机中的投影位置,通过最小化重投影误差(Reprojection error)来优化相机运动。在这个过程中,我们需要精确地知道空间点在两个相机中投影后的像素位置——这也就是我们为何要对特征进行匹配或跟踪的理由。同时,我们也知道,计算、匹配特征需要付出大量的计算量。相对的,在直接法中,我们并不需要知道点与点之间之间的对应关系,而是通过最小化光度误差(Photometric error)来求得它们。
光流(Optical Flow)
直接法是从光流演变而来的。它们非常相似,具有相同的假设条件。光流描述了像素在图像中的运动,而直接法则附带着一个相机运动模型。为了说明直接法,我们先来介绍一下光流。
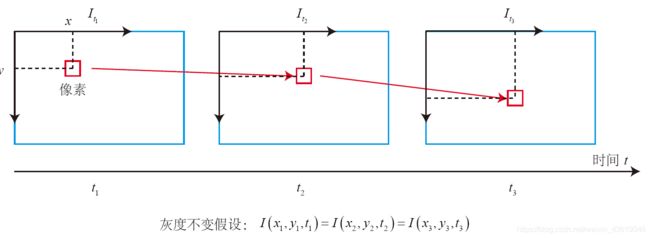
光流是一种描述像素随着时间,在图像之间运动的方法,如下图所示。随着时间的经过,同一个像素会在图像中运动,而我们希望追踪它的运动过程。计算部分像素运动的称为稀疏光流,计算所有像素的称为稠密光流。稀疏光流以Lucas-Kanade 光流为代表,并可以在SLAM 中用于跟踪特征点位置。因此,本节主要介绍Lucas-Kanade 光流,亦称LK光流。
直接法(Direct Methods)
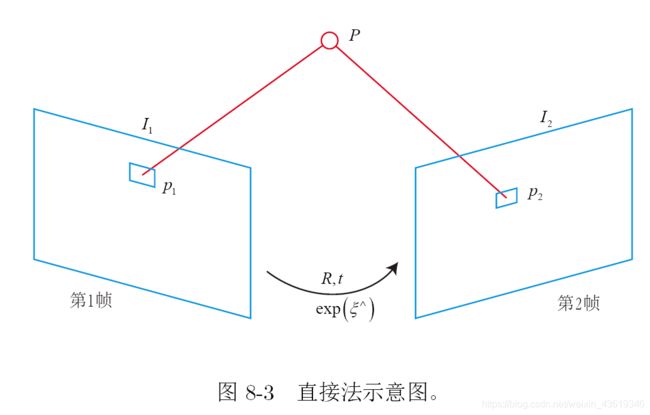
如图8-3所示,考虑某个空间点P 和两个时刻的相机。P 的世界坐标为[X; Y;Z],它在两个相机上成像,记非齐次像素坐标为p1; p2。我们的目标是求第一个相机到第二个相机的相对位姿变换。我们以第一个相机为参照系,设第二个相机旋转和平移为R; t(对应李代数为 ξ \xi ξ)。同时,两相机的内参相同,记为K。为清楚起见,我们列写完整的投影方程:



直接法的讨论
在我们上面的推导中,P 是一个已知位置的空间点,它是怎么来的呢?在RGB-D 相机下,我们可以把任意像素反投影到三维空间,然后投影到下一个图像中。如果在单目相机中,这件事情要更为困难,因为我们还需考虑由P 的深度带来的不确定性。详细的深度估计放到13 讲中讨论。现在我们先来考虑简单的情况,即P 深度已知的情况。根据P 的来源,我们可以把直接法进行分类:
- P 来自于稀疏关键点,我们称之为稀疏直接法。通常我们使用数百个至上千个关键点,并且像L-K 光流那样,假设它周围像素也是不变的。这种稀疏直接法不必计算描述子,并且只使用数百个像素,因此速度最快,但只能计算稀疏的重构。
- P 来自部分像素。我们看到式(8.16)中,如果像素梯度为零,整一项雅可比就为零,不会对计算运动增量有任何贡献。因此,可以考虑只使用带有梯度的像素点,舍弃像素梯度不明显的地方。这称之为半稠密(Semi-Dense)的直接法,可以重构一个半稠密结构。
- P 为所有像素,称为稠密直接法。稠密重构需要计算所有像素(一般几十万至几百万个),因此多数不能在现有的CPU 上实时计算,需要GPU 的加速。但是,如前面所讨论的,梯度不明显的点,在运动估计中不会有太大贡献,在重构时也会难以估计
位置。
可以看到,从稀疏到稠密重构,都可以用直接法来计算。它们的计算量是逐渐增长的。稀疏方法可以快速地求解相机位姿,而稠密方法可以建立完整地图。具体使用哪种方法,需要视机器人的应用环境而定。特别地,在低端的计算平台上,稀疏直接法可以做到非常快速的效果,适用于实时性较高且计算资源有限的场合。
最后,我们总结一下直接法的优缺点。大体来说,它的优点如下:
• 可以省去计算特征点、描述子的时间。
• 只要求有像素梯度即可,无须特征点。因此,直接法可以在特征缺失的场合下使用。比较极端的例子是只有渐变的一张图像。它可能无法提取角点类特征,但可以用直接法估计它的运动。
• 可以构建半稠密乃至稠密的地图,这是特征点法无法做到的。
另一方面,它的缺点也很明显:
• 非凸性——直接法完全依靠梯度搜索,降低目标函数来计算相机位姿。其目标函数中需要取像素点的灰度值,而图像是强烈非凸的函数。这使得优化算法容易进入极小,只在运动很小时直接法才能成功。
• 单个像素没有区分度。找一个和他像的实在太多了!——于是我们要么计算图像块,要么计算复杂的相关性。由于每个像素对改变相机运动的“意见”不一致。只能少数服从多数,以数量代替质量。
• 灰度值不变是很强的假设。如果相机是自动曝光的,当它调整曝光参数时,会使得图像整体变亮或变暗。光照变化时亦会出现这种情况。特征点法对光照具有一定的容忍性,而直接法由于计算灰度间的差异,整体灰度变化会破坏灰度不变假设,使算法失
败。针对这一点,目前的直接法开始使用更细致的光度模型标定相机,以便在曝光时间变化时也能让直接法工作。
实践部分
optical_flow:
运行结果:
/home/wh/shenlan/slambook2/ch8/cmake-build-debug/optical_flow /home/wh/shenlan/slambook2/ch8/LK1.png /home/wh/shenlan/slambook2/ch8/LK2.png
build pyramid time: 0.000126968
track pyr 3 cost time: 0.000216852
track pyr 2 cost time: 0.00022815
track pyr 1 cost time: 0.000221607
track pyr 0 cost time: 0.000217817
optical flow by gauss-newton: 0.00153844
optical flow by opencv: 0.00237133
分别为单层光流、多层光流和OpenCV光流。
direct_method :
第 8 讲的直接法实现,需要使用 OpenCV 4 支持的 cv::parallel_for_ 函数。如果读者使用较旧的版本,需要对代码做一些改动。具体的改动方法请参照对应版本的 OpenCV 文档,或者参考这里。
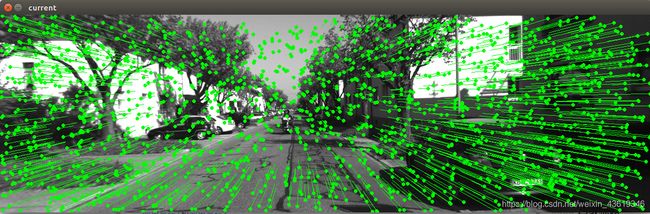
效果为:
清楚一些的图:
课后习题
1. 除了LK 光流之外,还有哪些光流方法?它们各有什么特点?
简单总结1和简单总结2
2. 在本节的程序的求图像梯度过程中,我们简单地求了u+1 和u-1 的灰度之差除2,作为u 方向上的梯度值。这种做法有什么缺点?提示:对于距离较近的特征,变化应该较快;而距离较远的特征在图像中变化较慢,求梯度时能否利用此信息?
当被观测的特征点离相机距离比较小时,其像素的运动会明显加快,像素跨度会增大,像素的梯度不可能能被左右两个像素灰度值之和除以2的,而且这种方法也很容易被噪音影响以至于光流运算过程精度下降。当距离特别远时,容易速度变化过小,引起漂移。在求梯度时,对于不同深度的像素块可以分层优化求解。在式(8.16)中,像素梯度为0,整项雅可比矩阵就为零,不会对计算运动增量有任何贡献。
3. 在稀疏直接法中,假设单个像素周围小块的光度也不变,是否可以提高算法鲁棒性?请编程实现此事。
向大佬学习
分析:根据直接法的思想:基于灰度不变假设。因为题目假设了周围小块光度也不变,那么我们可以用单个像素周围的3x3或5x5小块的平均灰度值作为单个像素的灰度值,从一定程度上调高了健壮性,但是效果提升有限。
自己的实现待填坑
4. *使用Ceres 实现RGB-D 上的稀疏直接法和半稠密直接法。
前端不变,需要改一下优化过程。
5. 相比于RGB-D 的直接法,单目直接法往往更加复杂。除了匹配未知之外,像素的距离也是待估计的。我们需要在优化时把像素深度也作为优化变量。阅读[57, 59],你能理解它的原理吗?如果不能,请在13 讲之后再回来阅读。
LSD-SLAM算法主要创新点在于:
1.将深度噪声融入光度误差检测之中;
2.通过Sim(3)双向检测直接配准的方式实现了图优化中关键帧节点间边的构造。
但是这个算法存在着一些假设,甚至有些是强假设:
1.灰度不变性假设;(这个假设直接法都存在,属于强假设)
2.每一个像素的逆深度而不是深度服从高斯概率分布;(这个假设相较于假设深度服从高斯分布优越性较大,详细可以看我后续博客)
3.图像灰度噪声服从高斯分布;
4.像素的残差互相独立。(这个假设实际不成立,但是其在算法中保证了噪声在不同自由度之间的相关性)
单目SLAM中LSD-SLAM算是一种比较具有代表性的系统,通过对其代码的详细学习可以让我们更加深刻地了解单目SLAM地基本设计思路以及一些瓶颈问题。
6. 由于图像的非凸性,直接法目前还只能用于短距离,非自动曝光的相机。你能否提出增强直接法鲁棒性的方案?阅读[58, 60] 可能会给你一些灵感。
[58]直接稀疏测距(DSO)是一种基于新颖,高度精确的稀疏和直接结构和运动公式的视觉测距方法。它结合了完全直接的概率模型(最小化光度误差)和所有模型参数的一致联合优化,包括几何 - 表示为参考帧中的反向深度 - 和相机运动。这是通过省略先前在其他直接方法中使用的平滑度并且在整个图像中均匀地采样像素来实时实现的。由于我们的方法不依赖于关键点检测器或描述符,因此它可以自然地从具有强度梯度的所有图像区域中采样像素,包括基本无特征的墙壁上的边缘或平滑强度变化。所提出的模型集成了完整的光度校准,考虑了曝光时间,镜头渐晕和非线性响应功能。我们在包含几个小时视频的三个不同数据集上彻底评估我们的方法。实验表明,在跟踪精度和鲁棒性方面,所提出的方法在各种真实世界环境中明显优于现有技术的直接和间接方法。
[60]我们提出了一种用于立体摄像机的新型直接视觉惯性测距方法。通过最小化组合的光度和惯性能量功能来同时估计相机姿态,速度和IMU偏差。这使我们能够利用视觉和惯性数据的互补性。与此同时,与所有现有的视觉惯性方法相比,我们的方法是完全直接的:以半密集深度图的形式估计几何,而不是手动设计的稀疏关键点。深度信息既可以从静态立体声中获得 - 与立体相机的固定基线图像相关 - 和时间立体声相关 - 来自同一相机的图像,在不同的时间点拍摄。我们表明,我们的方法不仅优于仅视觉或松耦合方法,而且可以比不同数据集上最先进的基于关键点的方法获得更准确的结果,包括快速运动和显着的照明变化。此外,我们的方法提供高保真半密度,度量环境重建,并在CPU上实时运行。
由文中图像三维化显示不难发现,一般图像并不具备明显的凹凸性,其灰度值所形成的三维表面也是极其粗糙的。文献【60】Direct-Visual-Inertial-Odometry-with-Stereo-Cameras和文献【58】Direct Sparse Odometry都是LSD-SLAM的作者Jakob Engel参与的。这些文章都对图像的非凸性缺点进行了改良。
其中文献【60】主要是通过外加IMU传感器与光度误差紧耦合来克服实际图像中的光度误差的非凸性,主要是从构建最小能量函数和将IMU数据参与因子图优化来实现。因为IMU对于基体的短期位姿运动测量能够达到很精确的程度,但是长时间测量容易发生偏移,刚好视觉图像能起到纠正的作用,所以在此机理下,二者紧耦合能够取到不错的效果。详细算法及代码可以自行查看论文。
文献【58】是介绍DSO算法的文章。DSO算法算是直接法单目SLAM思想上比较成熟的一种算法。其中有很多比较先进的思想相较于以往的SLAM,包括对相机光度的重新修正,而且对于图像的非凸性,其也有解决的办法。在算法梯度下降时需要用到雅可比矩阵,DSO算法的雅可比矩阵主要包含三块,分别是图像雅可比、几何雅可比以及光度雅可比。后两者的值作者认为其相较于像素坐标变量而言是光滑的,所以只计算一次,但是图像雅可比显然不够光滑,作者设计了一种名为First Estimate Jacobian(FEJ)的优化方式。由于在优化的过程中会出现零空间(null space),边缘化操作容易导致零空间降维,所以FEJ强制让每一个地图点在同一时刻线性化,从而避免了零空间降维的发生,同时也保证了计算算量。
对于直接法健壮性增强的方法还有很多,但是能不真正增加计算量的方法却很少(前面提到的块操作也是一种)。直接法属于一种直接数据关联的方法,这一点比特征点法强不少,但是其优化过程比BA问题复杂太多,而且如果初始值估计不好对后续算法收敛性有着很大的影响。对于直接法单目SLAM的学习还有待加强。