【计算机图形学】Liang-Barsky裁剪算法(C++实现)

背景

Cyrus-Beck算法的优化算法

思想

基本出发点是直线的参数方程

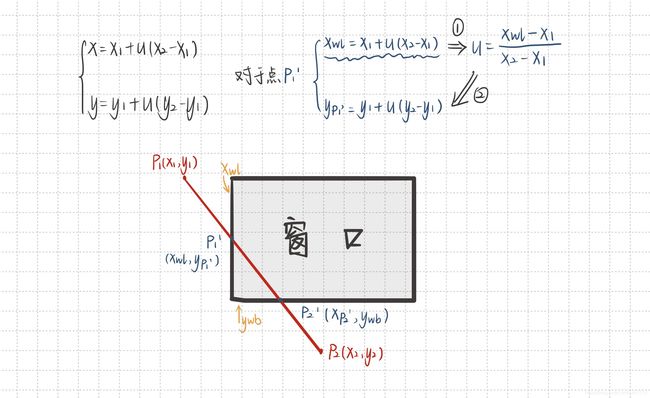
由图可知，只要求出u的取值即可求出yp1‘，从而得到线段与边界xwl交点坐标P1’（xwl，ywb，x1，x2，y1，y2都是已知的），同理可得P2‘。

推广到普遍情况，u的取值范围：

由点的裁剪公式（即点P(x,y)在裁剪窗口内必须满足）
推出：

将公式移位：

令
很眼熟有没有，就是上图的那个公式。

于是就有
upk 《=qk k=1，2，3，4

看到pk，我想到数学老师的嘶吼：“移动不等式一定要注意符号和0！”

所以，这里将pk分为三部分讨论

pk > 0 ，u <= qk/pk
pk < 0，u >=qk/pk
并且，根据参数方程0= 所以将u分为：

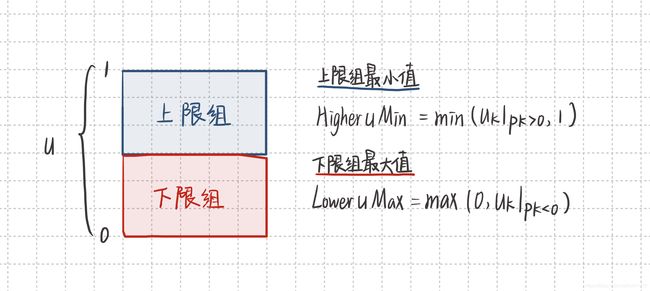
u的取值范围就很清晰了：（LoweruMax，HigheruMin）初始值为（0，1），把四个边界的x或y值带入u = qk/pk，k=1，2，3，4 ，依次比较，就可以求得u的取值范围。

实现代码

无交互版

/*
 *  Liang-Barsky算法
 *  直线段裁剪算法
 */
#include 
#include 
#include 
#define LINENUMBER 11
GLfloat lineX1[LINENUMBER] = {
      0.1f,0.5f,0.9f,1.0f,0.1f,0.2f,0.1f,0.7f,0.9f,0.5f,0.1f }, lineY1[LINENUMBER] = {
      0.1f,0.3f,0.7f,0.9f,0.5f,0.1f,0.1f,0.1f,0.2f,0.1f,0.7f }, lineX2[LINENUMBER] = {
      0.8f,0.4f,0.7f,0.7f,0.5f,0.2f,0.1f,0.4f,0.7f,0.7f,0.9f }, lineY2[LINENUMBER] = {
      0.8f,0.6f,0.4f,0.9f,0.1f,1.0f,1.0f,0.4f,0.7f,0.7f,0.7f };//定义被裁减线段的两个端点
GLfloat CutlineX1[LINENUMBER], CutlineX2[LINENUMBER], CutlineY1[LINENUMBER], CutlineY2[LINENUMBER];//裁剪后的线段
GLfloat XWL = 0.2f, XWR = 0.8f, YWB = 0.3f, YWT = 0.7f;//定义裁减边界

void myinit(void)
{
     
	glShadeModel(GL_FLAT);
	glClearColor(0.0, 0.0, 0.0, 0.0);
}

void myReshape(int w, int h)
{
     
	glViewport(0, 0, w, h);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	if (w <= h)
		gluOrtho2D(0.0, 1.0, 0.0, 1.0*(GLfloat)h / (GLfloat)w);
	else
		gluOrtho2D(0.0, 1.0*(GLfloat)w / (GLfloat)h, 0.0, 1.0);
	glMatrixMode(GL_MODELVIEW);
}


bool Intersection(GLfloat p, GLfloat q, GLfloat &LoweruMax, GLfloat &HigheruMin)//判断交点，求u的范围
{
     
	if (q < 0) return 0;//线段不在裁剪框内
	GLfloat u = q / p;
	if(( u < 0 )|| ( u > 1)) return 1;

	if (p < 0)//p小于0，u在下限组取最大值
	{
     
		if (u > LoweruMax) LoweruMax = u;
	}

	else if (p > 0)//p大于0，u在上限组取最小值
	{
     
		if (u < HigheruMin) HigheruMin = u;
	}

	return 1;
}


void myclip()//裁剪算法
{
     
	GLfloat deltaX, deltaY;
	for (int i = 0; i < LINENUMBER; i++)
	{
     
		GLfloat LoweruMax = 0.0f;//定义上限组，下限组
		GLfloat HigheruMin = 1.0f;
		//下限组最大值LoweruMax和上限组最小值HigheruMin，以及裁剪边框
		deltaX = lineX2[i] - lineX1[i];
		deltaY = lineY2[i] - lineY1[i];

		if (Intersection(-deltaX, lineX1[i] - XWL, LoweruMax, HigheruMin))//判断左边界交点
		{
     
			if (Intersection(deltaX, XWR - lineX1[i], LoweruMax, HigheruMin))//判断右边界交点
			{
     
				if (Intersection(-deltaY, lineY1[i] - YWB, LoweruMax, HigheruMin))//判断下边界交点)
				{
     
					if (Intersection(deltaY, YWT - lineY1[i], LoweruMax, HigheruMin))//判断上边界交点
					{
     
						CutlineX1[i] = lineX1[i] + LoweruMax * deltaX;//裁剪后的交点
						CutlineY1[i] = lineY1[i] + LoweruMax * deltaY;

						CutlineX2[i] = lineX1[i] + HigheruMin * deltaX;
						CutlineY2[i] = lineY1[i] + HigheruMin * deltaY;
					}
				}
			}
		}	
	}
}


void display(void)
{
     
	glClear(GL_COLOR_BUFFER_BIT);
	// 裁剪框	
	glColor4f(1.0, 1.0, 1.0, 0.4);
	glBegin(GL_POLYGON);
	glVertex2f(XWL, YWT); 
	glVertex2f(XWR, YWT); 
	glVertex2f(XWR, YWB);
	glVertex2f(XWL, YWB);
	glEnd();
	// 画线
	for (int i = 0; i < LINENUMBER; i++)
	{
     
		glBegin(GL_LINES);//裁剪前为白色
		glColor3f(0.0f, 1.0f, 0.0f);
		glVertex2f(lineX1[i], lineY1[i]);
		glVertex2f(lineX2[i], lineY2[i]);
		glEnd();
	}

	myclip();
	
	// 画出裁剪后的线
	for (int i = 0; i < LINENUMBER; i++)
	{
     
		glLineWidth(3);
		glBegin(GL_LINES);//裁剪后为红色
		glColor3f(1.0f, 0.0f, 0.0f);
		glVertex2f(CutlineX1[i], CutlineY1[i]);
		glVertex2f(CutlineX2[i], CutlineY2[i]);
		glEnd();
	}

	glFlush();
}


int main(int argc, char** argv)
{
     
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
	
	glutInitWindowSize(500, 500);
	glutInitWindowPosition(100, 100);
	glutCreateWindow(argv[0]);

	myinit();

	glutDisplayFunc(display);
	glutReshapeFunc(myReshape);
	
	glutMainLoop();

	return 1;
}

交互版

参考

• [计算机图形学经典算法] Liang-Barsky（梁友栋-Barsky） 算法 （附Matlab代码）（看了这位老哥的博客我才懂了！）