【算法】常用的几种经典排序算法
文章目录
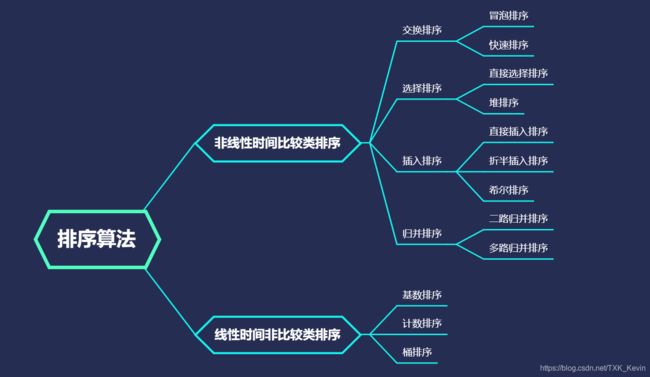
- 一、算法概述
-
- 1. 基本概念
- 2. 算法分类
- 3. 算法复杂度
- 二、算法实现
-
- 1. 交换排序
-
- 1.1. 冒泡排序(Bubble Sort)
- 1.2. 快速排序(Quick Sort)
- 2. 选择排序
-
- 2.1. 直接选择排序(Straight Selection Sort)
- 2.2. 堆排序(Heap Sort)
- 3. 插入排序
-
- 3.1. 直接插入排序(Straight Insertion Sort)
- 3.2. 折半插入排序(Binary Insertion Sort)
- 3.3. 希尔排序(Shell Sort)
- 4. 归并排序
-
- 4.1. 二路归并排序(Binary Merge Sort)
- 5. 非比较类排序
-
- 5.1. 基数排序(Radix Sort)
- 5.2. 计数排序(Counting Sort)
- 5.3. 桶排序(Bucket Sort)
- 写在最后
一、算法概述
1. 基本概念
(1)外部排序和内部排序
- 内部排序:指在排序期间数据对象所有存放在内存的排序。(本文所讨论的都是内部排序算法)
- 外部排序:指在排序期间所有对象占用的空间太大,以致于不能在同一时间内存放在内存中,这些对象必须依据排序过程,不断在内、外存间移动已完成外部排序。
(2)排序算法的稳定性
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
(3)算法的时空复杂度
- 时间复杂度 是指执行算法所需要的计算工作量。
- 空间复杂度 是指执行这个算法所需要的内存空间。
2. 算法分类
常见排序算法可以分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn)因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
3. 算法复杂度
| 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 快速排序 | O(n log2n) | O(n log2n) | O(n2) | O(log2n) | 不稳定 |
| 直接选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 |
| 堆排序 | O(n log2n) | O(n log2n) | O(n log2n) | O(1) | 不稳定 |
| 直接插入排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 折半插入排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 希尔排序 | O(n log2n) | O(n) | O(n2) | O(1) | 不稳定 |
| 归并排序 | O(n log2n) | O(n log2n) | O(n log2n) | O(n) | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | O(n2) | O(n+k) | 稳定 |
二、算法实现
注:本文使用Python来实现以下几种排序算法。其中,调用random.randint()方法的目的是产生初始随机序列以供排序。
1. 交换排序
1.1. 冒泡排序(Bubble Sort)
(1)算法思路:
(1)比较相邻的元素。如果第一个比第二个大,就交换它们两个;
(2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
(3)针对所有的元素重复以上的步骤,除了最后一个;
(4)重复步骤①②③,直到排序完成。
(2)算法实现:
from random import randint
def bubbleSort(numList): # 冒泡排序
for i in range(len(numList)-1):
isSorted = True
for j in range(len(numList)-i-1):
if numList[j]>numList[j+1]:
numList[j], numList[j+1] = numList[j+1], numList[j]
isSorted = False
if isSorted==True:
break # 若一轮排序后仍不发生元素交换,则说明排序已完成
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("冒泡排序前:", numList)
numList = bubbleSort(numList) # 冒泡排序
print("冒泡排序后:", numList)
实验结果:
冒泡排序前: [73, 21, 53, 76, 62, 35, 59, 21, 19, 43]
冒泡排序后: [19, 21, 21, 35, 43, 53, 59, 62, 73, 76]
1.2. 快速排序(Quick Sort)
(1)算法思路:
(1)从数列中挑出一个元素,称为 “基准”;
(2)重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
(3)递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
(2)算法实现:
from random import randint
def partition(numList, left, right):
standard = numList[left]
while left<right :
while left<right and standard<=numList[right] :
right -= 1
if left<right and standard>numList[right] :
numList[left] = numList[right]
left += 1
while left<right and standard>=numList[left] :
left += 1
if left<right and standard<numList[left] :
numList[right] = numList[left]
right -= 1
numList[left] = standard
return left
def quickSort(numList, left, right): # 快速排序
if left<right :
mid = partition(numList, left, right)
numList = quickSort(numList, left, mid-1)
numList = quickSort(numList, mid+1, right)
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("快速排序前:", numList)
numList = quickSort(numList, 0, len(numList)-1) # 快速排序
print("快速排序后:", numList)
实验结果:
快速排序前: [87, 57, 15, 93, 88, 100, 13, 18, 7, 67]
快速排序后: [7, 13, 15, 18, 57, 67, 87, 88, 93, 100]
2. 选择排序
2.1. 直接选择排序(Straight Selection Sort)
(1)算法思路:
(1)设array一个需要排序的数组,最初时的未排序序列unsortedArray为整个数组array。
(2)首先从前向后扫描整个未排序序列,在未排序序列中找到最小元素,与该序列的首元素进行交换。每次遍历后,未排序序列中的最小元素将被移动到已排序序列末尾,并且已确定位置的数据不需要再参与排序,这样一来就缩小了未排序序列unsortedArray。
(3)重复步骤②,直到所有元素均排序完毕。
(2)算法实现:
from random import randint
def selectSort(numList): # 简单选择排序
for i in range(len(numList)-1):
index = i # 指向待排序序列中最小元素的下标
for j in range(i+1, len(numList)):
if numList[index]>numList[j]:
index = j
numList[index], numList[i] = numList[i], numList[index]
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("简单选择排序前:", numList)
numList = selectSort(numList)
print("简单选择排序后:", numList)
实验结果:
简单选择排序前: [52, 2, 25, 77, 80, 52, 51, 67, 72, 0]
简单选择排序后: [0, 2, 25, 51, 52, 52, 67, 72, 77, 80]
2.2. 堆排序(Heap Sort)
(1)算法思路:
(1)将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
(2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
(3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
(2)算法实现:
from random import randint
def maxHeapify(heap, start, end):
parent, son = start, start*2 + 1 # 设置初始值
while son<=end :
if son<end and heap[son]<heap[son+1] :
son += 1
if heap[son]<=heap[parent] :
break
heap[parent], heap[son] = heap[son], heap[parent]
parent, son = son, 2*son + 1 # 更新数据值
def heapSort(heap): # 堆排序
size = len(heap)
for start in range(size//2, 0, -1):
maxHeapify(heap, start-1, size-1)
for end in range(size-1, 0, -1):
heap[0], heap[end] = heap[end], heap[0]
maxHeapify(heap, 0, end-1)
return heap
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("堆排序前:", numList)
numList = heapSort(numList) # 堆排序
print("堆排序后:", numList)
实验结果:
堆排序前: [52, 50, 6, 80, 1, 88, 28, 81, 25, 51]
堆排序后: [1, 6, 25, 28, 50, 51, 52, 80, 81, 88]
3. 插入排序
3.1. 直接插入排序(Straight Insertion Sort)
(1)算法思路:
(1)从第一个元素开始,该元素可以认为已经被排序;
(2)取出下一个元素,在已经排序的元素序列中从后向前扫描;
(3)如果该已排序元素大于新元素,将该元素移到下一位置;
(4)重复步骤③,直到找到已排序的元素小于或者等于新元素的位置;
(5)将新元素插入到该位置后;
(6)重复步骤②~⑤,直到排序完成。
(2)算法实现:
from random import randint
def insertSort(numList): # 直接插入排序
for no in range(1, len(numList)):
index = no - 1 # 指向当前插入点
num = numList[no] # 当前待插入的元素
while index>=0 and numList[index]>num :
numList[index+1] = numList[index]
index -= 1
numList[index+1] = num
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("直接插入排序前:", numList)
numList = insertSort(numList) # 直接插入排序
print("直接插入排序后:", numList)
实验结果:
直接插入排序前: [57, 65, 35, 11, 39, 10, 13, 10, 67, 72]
直接插入排序后: [10, 10, 11, 13, 35, 39, 57, 65, 67, 72]
3.2. 折半插入排序(Binary Insertion Sort)
(1)算法思路:
(1)设现有一个数组a需要排序,从第一个元素开始,该元素可以认为已经被排序;
(2)将待插入区域的首元素下标为 left,末元素下标记为 right,mid = (left+right)/2;取出下一个元素next,比较 next 和 a[mid] 的大小;
(3)如果 next 大于 a[mid],选择 a[mid+1] 到 a[right] 为新的插入区域(即令 left = mid+1 );否则选择a[left]到a[m-1]为新的插入区域(即令 right = mid-1 );
(4)重复步骤③,直至 left > right 为止,接着将 right 位置之后所有元素向后移一位,并将新元素next插入 a[high+1];
(5)重复步骤②③④,直到排序完成。
(2)算法实现:
from random import randint
def insertSort(numList): # 折半插入排序
for no in range(len(numList)):
num = numList[no] # 当前待插入的元素
# left、right代表已排序的序列的首、尾元素下标
left, right = 0, no-1
# 找到插入点的下标
while left<=right:
mid = (left + right) // 2
if numList[mid]>num :
right = mid - 1
else:
left = mid + 1
# 插入数据
index = no - 1
while index>=left:
numList[index+1] = numList[index]
index -= 1
numList[index+1] = num
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("折半插入排序前:", numList)
numList = insertSort(numList) # 折半插入排序
print("折半插入排序后:", numList)
实验结果:
折半插入排序前: [59, 15, 29, 0, 89, 45, 25, 26, 51, 86]
折半插入排序后: [0, 15, 25, 26, 29, 45, 51, 59, 86, 89]
3.3. 希尔排序(Shell Sort)
(1)算法思路:
设现有一个待排序数组,span(初值为数组长度的一半)为增量值:
(1)根据增量值span把整个数组划分为span个子序列(其中,每个子数组相邻俩元素的下标相差span,然后对各个子序列进行直接插入排序,接着将span缩小为原来的一半。
(2)重复步骤①,直到span小于1。
(2)算法实现:
from random import randint
def shellSort(numList): # 希尔排序
span = len(numList)//2 # 跨度值
while span>=1 :
for i in range(span):
for j in range(i+span, len(numList), span):
temp = numList[j] # 当前待排序的元素
index = j - span # 已排序序列的尾元素下标
while index>=0 and numList[index]>temp :
numList[index + span] = numList[index]
index -= span
numList[index + span] = temp
span //= 2
return numList
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("希尔排序前:", numList)
numList = shellSort(numList) # 希尔排序
print("希尔排序后:", numList)
实验结果:
希尔排序前: [25, 64, 87, 3, 20, 92, 96, 6, 35, 51]
希尔排序后: [3, 6, 20, 25, 35, 51, 64, 87, 92, 96]
4. 归并排序
4.1. 二路归并排序(Binary Merge Sort)
(1)算法思路:
(1)设现有一个待排序数组,将数组均分成左部子数组left和右部子数组right。如果子数组内部数据是无序的,则对子数组递归进行二分,直至分解出的小组只有一个元素,此时认为该小组内部有序。
(2)合并两个有序子数组,比较两个子数组的最前面的数,谁小就先取谁,该数组的指针往后移一位。
(3)重复步骤②,直至一个数组为空,然后把另一个数组的剩余部分复制过来即可。
(4)重复步骤②③,直至所有子数组归并成一个数组。
(2)算法实现:
from random import randint
def Merge(left, right): # 归并序列
result = []
i, j = 0, 0
while i<len(left) and j<len(right) :
if left[i]<right[j] :
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
if i<len(left):
result.extend(left[i : ])
if j<len(right):
result.extend(right[j : ])
return result
def mergeSort(numList): # 二路归并排序
if len(numList)<=1:
return numList
size = (len(numList)) // 2
left = mergeSort(numList[:size])
right = mergeSort(numList[size:])
result = Merge(left, right)
return result
if __name__=="__main__":
numList = [randint(0, 100) for i in range(10)]
print("二路归并排序前:", numList)
numList = mergeSort(numList) # 二路归并排序
print("二路归并排序后:", numList)
实验结果:
二路归并排序前: [46, 77, 12, 91, 78, 6, 100, 86, 60, 2]
二路归并排序后: [2, 6, 12, 46, 60, 77, 78, 86, 91, 100]
5. 非比较类排序
5.1. 基数排序(Radix Sort)
(1)算法思路:
(1)将所有待比较的整数统一为同样的数位长度,数位较短的数前面补零;
(2)从最低位开始,依次进行一次排序;
(3)从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
(2)算法实现:
from random import randint
def radixSort(numList): # 基数排序
# (1) 找出最大值并求出其位数:
max_digit, maxium = 1, max(numList)
while maxium >= 10**max_digit:
max_digit += 1
# (2) 从个位开始,每研究一个数位就进行一次排序:
digit = 0
while digit < max_digit:
cur, temp = 0, 10**digit
table = [[] for i in range(19)] # 记录某位出现-9~9的整数
# (2-1) 根据整数某位的取值对号入座:
for num in numList:
# (因为余数始终为正数,这里需讨论正负性)
if num >= 0:
index = num // temp % 10 + 9
else:
index = 9 - (-num) // temp % 10
table[index].append(num)
# (2-2) 重新写回原数组,完成一次排序:
for lt in table:
for num in lt:
numList[cur] = num
cur += 1
digit += 1
return numList
if __name__ == "__main__":
numList = [randint(-200, 200) for i in range(10)]
print("基数排序前:", numList)
numList = radixSort(numList) # 基数排序
print("基数排序后:", numList)
实验结果:
基数排序前: [-46, 45, 32, -92, 18, 52, -31, -9, -50, -132]
基数排序后: [-92, -50, -46, -132, -31, -9, 18, 32, 45, 52]
5.2. 计数排序(Counting Sort)
(1)算法思路:
(1)找出待排序的数组中最大和最小的元素;
(2)统计数组中介于最值之间的每个值的元素出现的次数;
(3)依据统计的出现次数将数值反向填充目标数组。
(2)算法实现:
from random import randint
def countingSort(numList):
# (1) 找出数组numList中的最值:
maxium, minium = max(numList), min(numList)
# (2) 建立一个列表统计最值间每个整数出现的次数:
tabLen = maxium - minium + 1
table = [0] * tabLen
# (3) 统计最值间每个整数出现的次数:
for num in numList:
index = num - minium # 找出num对应的容器下标
table[index] += 1 # num出现的次数加 1
# (4) 反向填充目标数组:
cur = 0 # 当前应填充的数组元素下标
for idx in range(tabLen):
while table[idx] > 0:
numList[cur] = idx + minium
cur += 1
table[idx] -= 1
return numList
if __name__=="__main__":
numList = [randint(-200, 200) for i in range(10)]
print("计数排序前:", numList)
numList = countingSort(numList) # 计数排序
print("计数排序后:", numList)
实验结果:
计数排序前: [-32, 71, -86, 61, -123, 7, -138, -188, 49, 150]
计数排序后: [-188, -138, -123, -86, -32, 7, 49, 61, 71, 150]
5.3. 桶排序(Bucket Sort)
(1)算法思路:
(1)设置固定数量的空桶;
(2)把数据放到对应的桶中;
(3)对每个不为空的桶中数据进行排序;
(4)拼接不为空的桶中数据,得到结果。
(2)算法实现:
from random import randint
def insertionSort(array): # 直接插入排序
for no in range(1, len(array)):
cur = no - 1 # 指向当前插入点
num = array[no] # 当前待插入的元素
while cur >= 0 and array[cur] > num:
array[cur+1] = array[cur]
cur -= 1
array[cur+1] = num
return array
def bucketSort(numList):
# (1) 设置桶的数量(默认为5):
if len(numList) == 0:
return None
bucketNum = 5 if len(numList) > 5 else len(numList)
bucketList = [[] for i in range(bucketNum)]
# (2) 找出数组numList中的最值,设置好桶内间隔:
maxium, minium = max(numList), min(numList)
gap = (maxium - minium)//bucketNum + 1 # 桶内数字的间隔
# (3) 将数字装入桶中:
for num in numList:
index = (num - minium)//gap # 获取num所属桶的编号
bucketList[index].append(num)
# (4) 为每个桶里面的数字进行排序:
cur = 0
for bucket in bucketList:
bucket = insertionSort(bucket) # 插入排序
for num in bucket:
numList[cur] = num
cur += 1
return numList
if __name__ == "__main__":
numList = [randint(-100, 100) for i in range(10)]
print("桶排序前:", numList)
numList = bucketSort(numList) # 桶排序
print("桶排序后:", numList)
实验结果:
桶排序前: [54, 62, 82, 96, -61, -82, -15, -55, 35, -49]
桶排序后: [-82, -61, -55, -49, -15, 35, 54, 62, 82, 96]
写在最后
- 如果您发现文章存在问题,或者如果您有更好的建议,欢迎在下方评论区中留言讨论~
- 本文参考文章:十大经典排序算法(动图演示) - 博客园