【NLP】5计数词向量底层代码编写和gensim word2vec库入门——斯坦福大学CS224n第一次课作业代码复现

这是斯坦福大学CS224n课程的第一次课作业，下载之后打开其中的jupyter notebook：

 jupyter notebook exploring_word_vectors.ipynb

背景：词向量

词向量经常被用作下游NLP任务的基础组件，例如问题回答、文本生成、翻译等，因此建立一些关于其优缺点的直觉是很重要的。在这里，你将探讨两种类型的词向量：从共现矩阵衍生的词向量，以及通过GloVe衍生的词向量

关于术语的说明。"词向量 "和 "词嵌入 "这两个术语经常互换使用。术语 "嵌入 "指的是我们在一个较低维度的空间中对一个词的含义进行编码。正如维基百科所说，“从概念上讲，它涉及到一个数学嵌入，从一个每个单词只有一个维度的空间到一个维度更低的连续向量空间”

第一部分：基于计数的词向量

大多数词条向量模型都是从以下想法开始的：

你会知道一个词，从它周围的上下文(Firth, J. R. 1957:11)

许多词向量的实现是由类似的词，即（近似的）同义词，将在类似的语境中使用的想法驱动的。因此，类似的单词经常会和一个共享的单词子集（即上下文）一起被说或写。通过研究这些语境，我们可以尝试为我们的单词开发嵌入。考虑到这种直觉，许多 "老派 "的构建单词向量的方法都依赖于单词计数。在这里，我们对其中的一种策略–共现矩阵进行了详细的阐述（更多信息，请看这里或这里）

共现矩阵

共同出现矩阵统计事物在某种环境中共同出现的频率。给定文档中出现的某个词$w_i$，我们考虑周围的上下文窗口。假设我们的固定窗口大小为 ，那么这就是该文档中的前个和后个词，即词$w_{i-n}...w_{i-1}$和$w_{i+1}...w_{i+n}$ 。我们建立了一个共现矩阵 ，这是一个对称的逐字矩阵，其中$M_{ij}$是所有文档中$w_j$出现在$w_i$的窗口内的次数

例子: 固定窗口n=1的共现

文件1：“all that glitters is not gold”
文件2：“all is well that ends well”

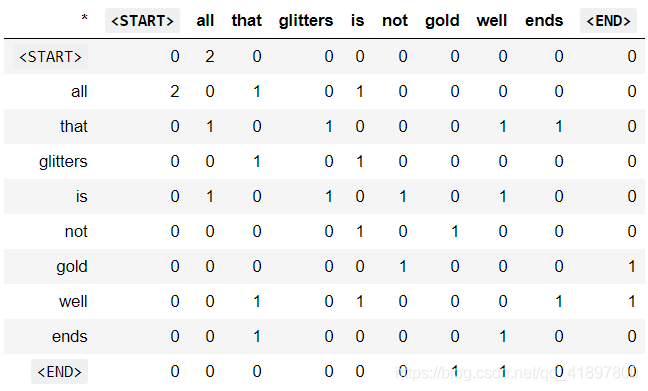
注：在NLP中，我们经常添加和标记来代表句子、段落或文档的开始和结束。在这种情况下，我们想象和标记囊括了每个文档，例如，" All that glitters is not gold "，并将这些标记包含在我们的共现计数中

该矩阵的行（或列）提供了一种类型的词向量（那些基于词-词共现的词向量），但一般来说，向量会很大（与语料库中不同词的数量呈线性关系）。因此，我们的下一步是运行维度降低。特别是，我们将运行SVD（Singular Value Decomposition，奇异值分解），这是一种广义的PCA（Principal Components Analysis，主成分分析），以选择顶部的主成分。这是一个用SVD降维的可视化。在这张图中，我们的共现矩阵是，有行对应个单词。我们得到一个完整的矩阵分解，奇异值排序在对角线矩阵中，我们新的、较短的长度-词向量在$U_k$中

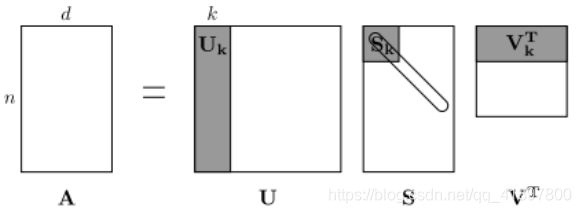
这种降低维度的共现表示法保留了词之间的语义关系，例如医生和医院会比医生和狗更接近

笔记。如果你连特征值是什么都记不住，这里有一个关于SVD的缓慢而友好的介绍。如果您想更彻底地了解PCA或SVD，请随时查看CS168的第7、8和9讲。这些课程笔记为这些通用算法提供了很好的高级处理方法。虽然，就本课而言，你只需要知道如何利用numpy、scipy或sklearn python包中这些算法的预编程实现来提取k维嵌入。在实践中，由于执行PCA或SVD所需内存，将完整的SVD应用于大型语料库是具有挑战性的。然而，如果你只想要相对较小的顶部向量分量–被称为Truncated SVD——那么有合理的可扩展技术来迭代计算这些分量

绘制共现词嵌入图

在这里，我们将使用路透社（商业和金融新闻）的语料库。如果您还没有运行本页顶部的导入单元，请现在就运行它（点击它并按 SHIFT-RETURN）。语料库由10,788个新闻文档组成，共130万字。这些文档横跨90个类别，分为训练和测试。更多细节，请参见此。我们在下面提供了一个read_corpus函数，它只提取 “原油”（即关于石油、天然气等的新闻文章）类别的文章。该函数还将和标记添加到每个文档中，并对单词进行小写。您不必进行任何其他类型的预处理

import nltk
nltk.download('reuters')

报错：

[nltk_data] Error loading reuters: 

解决方法：参考此文章或者直接下载，下载成功后在’C:\Users…\AppData\Roaming\nltk_data\corpora’可以找到’reuters.zip’文件，共6.08MB

import nltk

nltk.download('reuters')
from nltk.corpus import reuters

START_TOKEN = ''
END_TOKEN = ''


def read_corpus(category='crude'):      # 读取指定的Reuter的类别的文件，参数：category (string)：类别名称
    files = reuters.fileids(category)   #  Return：列表，包括每个处理过的文件中的字
    return [[START_TOKEN] + [w.lower() for w in list(reuters.words(f))] + [END_TOKEN] for f in files]

我们来看看这些文件是什么样的…

reuters_corpus = read_corpus()
import pprint
pprint.pprint(reuters_corpus[:3], compact=True, width=100)

问题1.1：实现distinct_words

写一个方法来计算出语料库中出现的不同的单词（单词类型）。你可以用 for循环来做这件事，但用 Python 列表理解来做会更有效。特别是，这可能对扁平化一个列表很有用。如果您不熟悉 Python 列表理解，这里有更多信息

你返回的corpus_words应该是排序的。你可以使用 python的sorted函数进行排序

您可能会发现使用Python set来删除重复的单词是很有用的，参考此文，代码如下：

def distinct_words(corpus):      # 为语料库确定一个不同的单词列表,参数：corpus (list of list of strings)： 语料库中的文件
    # corpus_words = []       # corpus_words (字符串列表): 语料库中不同单词的排序列表
    # num_corpus_words = -1       # num_corpus_words (整数)：整个语料库中不同的单词数量
    corpus_words = sorted(list({
     word for words in corpus for word in words}))
    num_corpus_words = len(corpus_words)

    return corpus_words, num_corpus_words

# 定义语料库
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
test_corpus_words, num_corpus_words = distinct_words(test_corpus)
# 正确的答案
ans_test_corpus_words = sorted([START_TOKEN, "All", "ends", "that", "gold", "All's", "glitters", "isn't", "well", END_TOKEN])
ans_num_corpus_words = len(ans_test_corpus_words)
# 检验正确的单词数量
assert(num_corpus_words == ans_num_corpus_words), "Incorrect number of distinct words. Correct: {}. Yours: {}".format(ans_num_corpus_words, num_corpus_words)
# 检验正确的单词
assert (test_corpus_words == ans_test_corpus_words), "Incorrect corpus_words.\nCorrect: {}\nYours:   {}".format(str(ans_test_corpus_words), str(test_corpus_words))
# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

结果：

--------------------------------------------------------------------------------
Passed All Tests!
--------------------------------------------------------------------------------

问题1.2：实现compute_co_occurrence_matrix

编写一个方法，为一定的窗口大小的（默认为4）构建一个共现矩阵，考虑到窗口中心的字之前和之后的字。在这里，我们开始使用numpy（np）来表示向量、矩阵和时序。如果你不熟悉numPy，在这个cs231n Python NumPy教程的后半部分有一个numPy教程

import numpy as np

def compute_co_occurrence_matrix(corpus, window_size=4):        # 为给定的语料库和window_size（默认为4）计算共现矩阵,文档中的每个词都应该在一个窗口的中心。靠近边缘的词会有一个较小的共现词数
    # 例如，如果我们把文档 " All that glitters is not gold "窗口大小为4，'All'将与""、"that"、"glitters"、"is "和 "not "共同出现
    # 参数：corpus：文档语料库；window_size：上下文窗口的大小
    # 返回：M(一个对称的numpy形状矩阵(语料库中的唯一词数))——词数的共现矩阵，词的行/列的排序应该与 distinct_words 函数给出的词的排序相同，word2ind (dict)：将词与矩阵M的索引（即行/列号）映射的字典

    words, num_words = distinct_words(corpus)
    M = None
    word2ind = {
     }

    M = np.zeros((num_words, num_words))
    word2ind = {
     word:i for i,word in enumerate(words)}      # 返回 enumerate(枚举) 对象

    for doc in corpus:
        for i, word in enumerate(doc):
            for j in range(i-window_size, i+window_size+1):
                if j < 0 or j >= len(doc):
                    continue
                if j != i:
                    M[word2ind[word], word2ind[doc[j]]] += 1

    return M, word2ind

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness.
# ---------------------

# Define toy corpus and get student's co-occurrence matrix
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
M_test, word2ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)

# Correct M and word2ind
M_test_ans = np.array(
    [[0., 0., 0., 0., 0., 0., 1., 0., 0., 1.,],
     [0., 0., 1., 1., 0., 0., 0., 0., 0., 0.,],
     [0., 1., 0., 0., 0., 0., 0., 0., 1., 0.,],
     [0., 1., 0., 0., 0., 0., 0., 0., 0., 1.,],
     [0., 0., 0., 0., 0., 0., 0., 0., 1., 1.,],
     [0., 0., 0., 0., 0., 0., 0., 1., 1., 0.,],
     [1., 0., 0., 0., 0., 0., 0., 1., 0., 0.,],
     [0., 0., 0., 0., 0., 1., 1., 0., 0., 0.,],
     [0., 0., 1., 0., 1., 1., 0., 0., 0., 1.,],
     [1., 0., 0., 1., 1., 0., 0., 0., 1., 0.,]]
)
ans_test_corpus_words = sorted([START_TOKEN, "All", "ends", "that", "gold", "All's", "glitters", "isn't", "well", END_TOKEN])
word2ind_ans = dict(zip(ans_test_corpus_words, range(len(ans_test_corpus_words))))

# Test correct word2ind
assert (word2ind_ans == word2ind_test), "Your word2ind is incorrect:\nCorrect: {}\nYours: {}".format(word2ind_ans, word2ind_test)

# Test correct M shape
assert (M_test.shape == M_test_ans.shape), "M matrix has incorrect shape.\nCorrect: {}\nYours: {}".format(M_test.shape, M_test_ans.shape)

# Test correct M values
for w1 in word2ind_ans.keys():
    idx1 = word2ind_ans[w1]
    for w2 in word2ind_ans.keys():
        idx2 = word2ind_ans[w2]
        student = M_test[idx1, idx2]
        correct = M_test_ans[idx1, idx2]
        if student != correct:
            print("Correct M:")
            print(M_test_ans)
            print("Your M: ")
            print(M_test)
            raise AssertionError("Incorrect count at index ({}, {})=({}, {}) in matrix M. Yours has {} but should have {}.".format(idx1, idx2, w1, w2, student, correct))

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

结果：

--------------------------------------------------------------------------------
Passed All Tests!
--------------------------------------------------------------------------------

问题1.3：实现reduce_to_k_dim

构建一种方法，对矩阵进行降维，生成k维嵌入。使用SVD取前k个分量，生成一个新的k维嵌入矩阵

注意：所有的numpy、scipy和scikit-learn（sklearn）都提供了一些SVD的实现，但只有scipy和sklearn提供了Truncated SVD的实现，而且只有sklearn提供了计算大规模Truncated SVD的高效随机算法。所以请使用sklearn.decomposition.TruncatedSVD

from sklearn.decomposition import TruncatedSVD

def reduce_to_k_dim(M, k=2):        # 减少一个共现矩阵(num_corpus_words, num_corpus_words)的维度到另一个维度的矩阵(num_corpus_words, k)
    # 使用以下Scikit-Learn的SVD函数：http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html
    # 参数：M (numpy matrix of shape (number of unique words in the corpus , number of unique words in the corpus))：词数的共同出现矩阵； k (int)：维度缩小后每个词的嵌入大小
    # 返回：M_reduced (numpy matrix of shape (number of corpus words, k)): k维的词嵌入矩阵
    # 从数学类的SVD来看，这实际上是返回U * S
    n_iters = 10        # 在调用 "TruncatedSVD "时使用此参数
    M_reduced = None

    svd = TruncatedSVD(n_components=k, n_iter=n_iters)
    M_reduced = svd.fit_transform(M)

    print('Done.')
    return M_reduced

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness
# In fact we only check that your M_reduced has the right dimensions.
# ---------------------

# Define toy corpus and run student code
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]
M_test, word2ind_test = compute_co_occurrence_matrix(test_corpus, window_size=1)
M_test_reduced = reduce_to_k_dim(M_test, k=2)

# Test proper dimensions
assert (M_test_reduced.shape[0] == 10), "M_reduced has {} rows; should have {}".format(M_test_reduced.shape[0], 10)
assert (M_test_reduced.shape[1] == 2), "M_reduced has {} columns; should have {}".format(M_test_reduced.shape[1], 2)

# Print Success
print ("-" * 80)
print("Passed All Tests!")
print ("-" * 80)

结果：

Done.
--------------------------------------------------------------------------------
Passed All Tests!
--------------------------------------------------------------------------------

问题1.4：实现plot_embeddings

在这里，你将编写一个函数，在二维空间中绘制一组二维向量。对于图形，我们将使用Matplotlib（plt）

对于这个例子，你可能会发现改编这个代码很有用。在未来，一个好的方法是看Matplotlib图库，找到一个看起来有点像你想要的情节，然后改编他们给出的代码

import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [10, 5]

def plot_embeddings(M_reduced, word2ind, words):        # 在散点图中绘制 "单词 "列表中指定的单词的嵌入
    # 注意：不要绘制M_reduced / word2ind中列出的所有单词，在每一个点旁边加上一个标签
    # 参数：M_reduced (numpy matrix of shape (number of unique words in the corpus , 2)): 2维词嵌入的矩阵；word2ind(dict)：将单词映射到矩阵M的索引的字典；words (list of strings)：我们要可视化嵌入的字词
    for word in words:
        coord = M_reduced[word2ind[word]]
        x = coord[0]
        y = coord[1]
        plt.scatter(x, y, marker='x', color='red')
        plt.text(x, y, word, fontsize=9)
    plt.show()

# ---------------------
# Run this sanity check
# Note that this is not an exhaustive check for correctness.
# The plot produced should look like the "test solution plot" depicted below.
# ---------------------

print ("-" * 80)
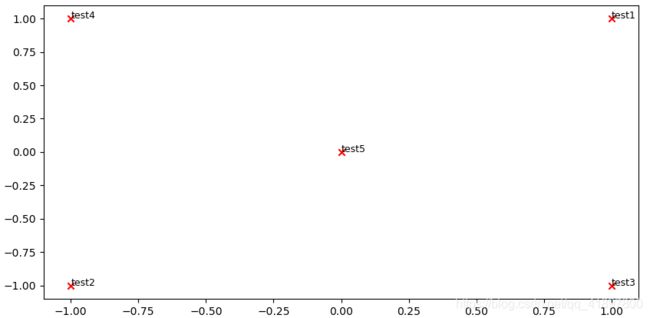
print ("Outputted Plot:")

M_reduced_plot_test = np.array([[1, 1], [-1, -1], [1, -1], [-1, 1], [0, 0]])
word2ind_plot_test = {
     'test1': 0, 'test2': 1, 'test3': 2, 'test4': 3, 'test5': 4}
words = ['test1', 'test2', 'test3', 'test4', 'test5']
plot_embeddings(M_reduced_plot_test, word2ind_plot_test, words)

print ("-" * 80)

问题1.5：共生图分析

现在，我们将把你写的所有部分放在一起 我们将在路透社的 “原油”（石油）语料库中，用固定的4窗口（默认窗口大小）计算共现矩阵。然后我们将使用TruncatedSVD来计算每个词的二维嵌入。TruncatedSVD返回的是U*S，所以我们需要对返回的向量进行归一化处理，这样所有的向量都会出现在单位圆的周围（因此紧密性是方向性的紧密性）。注意：下面这行做归一化的代码使用了NumPy的广播概念。如果你不知道广播，请查阅 Computation on Arrays: Broadcasting by Jake VanderPlas

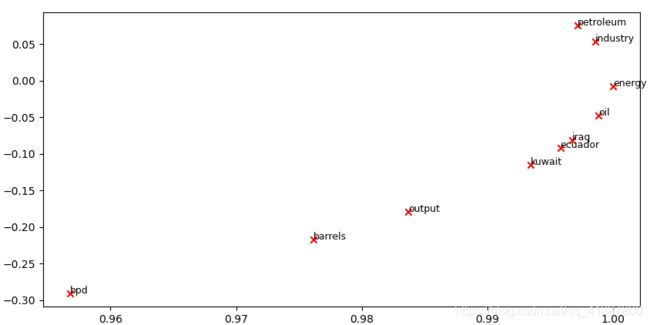
运行下面的单元格来生成图。大概需要几秒钟的时间来运行。在二维嵌入空间中，什么东西聚在一起？哪些没有聚在一起，而你认为应该聚在一起的？注："bpd "代表 “barrels per day”，是原油主题文章中常用的缩写

# -----------------------------
# Run This Cell to Produce Your Plot
# ------------------------------
reuters_corpus = read_corpus()
M_co_occurrence, word2ind_co_occurrence = compute_co_occurrence_matrix(reuters_corpus)
M_reduced_co_occurrence = reduce_to_k_dim(M_co_occurrence, k=2)

# Rescale (normalize) the rows to make them each of unit-length
M_lengths = np.linalg.norm(M_reduced_co_occurrence, axis=1)
M_normalized = M_reduced_co_occurrence / M_lengths[:, np.newaxis] # broadcasting

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']

plot_embeddings(M_normalized, word2ind_co_occurrence, words)

结果：

第二部分：基于词向量预测

正如在课堂上所讨论的那样，最近基于预测的词向量表现出了较好的性能，如word2vec和GloVe（它也利用了计数的优势）。在这里，我们将探讨GloVe产生的嵌入。关于word2vec和GloVe算法的更多细节，请重温课堂笔记和讲座幻灯片。如果你觉得冒险，可以挑战一下自己，尝试阅读GloVe的原创论文

然后运行以下单元格，将GloVe向量加载到内存中。注意：如果这是您第一次运行这些单元格，即下载嵌入模型，将需要几分钟的时间来运行。如果您之前已经运行过这些单元格，重新运行它们将加载模型而无需重新下载，这将需要大约1到2分钟

注意：如果你收到一个 "reset by peer "的错误，请重新运行该单元格以重新开始下载

降低单词嵌入的维度

让我们直接将GloVe嵌入与共现矩阵的嵌入进行比较。为了避免内存耗尽，我们将用10000个GloVe向量的样本来代替。运行以下单元格：

1. 将10000个Glove向量放入一个矩阵M中
2. 运行 reduce_to_k_dim(您的 Truncated SVD 函数) 将向量从 200 维减少到 2 维

import numpy as np

def get_matrix_of_vectors(wv_from_bin, required_words=['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']):
    # 将GloVe向量放入一个矩阵M中
    # 参数：wv_from_bin:KeyedVectors对象；从文件中加载的400000个GloVe向量
    # 返回：M：包含向量的numpy矩阵形状（num words，200）；word2ind: 字典将每个词映射到M中的行号上

    import random
    words = list(wv_from_bin.vocab.keys())
    print("Shuffling words ...")
    random.seed(224)        # seed()有参数时，每次生成的随机数是一样的，同时选择不同的参数生成的随机数也不一样
    random.shuffle(words)       # 将序列的所有元素随机排序
    words = words[:10000]
    print("Putting %i words into word2ind and matrix M..." % len(words))
    word2ind = {
     }
    M = []
    curInd = 0
    for w in words:
        try:
            M.append(wv_from_bin.word_vec(w))
            word2ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    for w in required_words:
        if w in words:
            continue
        try:
            M.append(wv_from_bin.word_vec(w))
            word2ind[w] = curInd
            curInd += 1
        except KeyError:
            continue
    M = np.stack(M)
    print("Done.")
    return M, word2ind

# -----------------------------------------------------------------
# Run Cell to Reduce 200-Dimensional Word Embeddings to k Dimensions
# Note: This should be quick to run
# -----------------------------------------------------------------
M, word2ind = get_matrix_of_vectors(wv_from_bin)
M_reduced = reduce_to_k_dim(M, k=2)

# Rescale (normalize) the rows to make them each of unit-length
M_lengths = np.linalg.norm(M_reduced, axis=1)
M_reduced_normalized = M_reduced / M_lengths[:, np.newaxis] # broadcasting

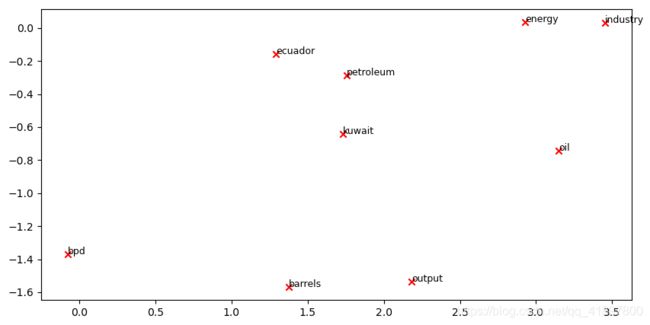
问题2.1：GloVe Plot分析

words = ['barrels', 'bpd', 'ecuador', 'energy', 'industry', 'kuwait', 'oil', 'output', 'petroleum', 'iraq']
plot_embeddings(M_reduced_normalized, word2ind, words)

报错：

KeyError: 'venezuela'

解决方法，把绘制二维词嵌入图像原：

coord = M_reduced[word2ind[word]]

改为：

try:
       coord = M_reduced[word2ind[word]]
except:
       print('No Key:{}'.format(word))
       continue

结果：No Key:venezuela

余弦相似性

现在我们有了词向量，我们需要一种方法来根据这些向量，量化各个词之间的相似度。一个这样的度量是余弦相似度。我们将用它来寻找彼此 "近 "和 "远 "的单词

我们可以把n维向量看作是n维空间中的点。如果我们从这个角度来看，L1和L2距离有助于量化 "我们必须走过 "的空间量来到达这两个点之间。另一种方法是研究两个向量之间的角度。从三角学中我们知道：

我们可以不计算实际的角度，而是用=(Θ)来代替相似性。形式上，两个向量和之间的余弦相似性定义为：
$$s=\frac{p\cdot q}{||p||||q||},\text{ where }s\in [-1,1]$$

问题2.2: 具有多重含义的词语

多义词和同义词是指有一个以上含义的词（参见本维基页面了解更多关于多义词和同义词的区别）。找出一个至少有两个不同意思的词，使前10个最相似的词（根据余弦相似度）包含两个意思的相关词。例如，"leaves"在前10名中同时有 "go_away "和 "a_structure_of_a_plant "两个意思，"leaves"同时有 "handed_waffle_cone "和 "lowdown "两个意思。你可能需要尝试几个多义词或同义词，才能找到一个

请说出你发现的词和前10名中出现的多义词。为什么你认为你试过的很多多义词或同义词都没有用（即前10名最相似的词只包含一个词的意思）？

注意: 您应该使用 wv_from_bin.most_similar(word)函数来获得前 10 个相似的单词。该函数根据与给定单词的余弦相似度对词汇中的所有其他单词进行排名。如需更多帮助，请查阅GenSim文档

wv_from_bin.most_similar("exciting")

[('interesting', 0.7734052538871765), ('fascinating', 0.6873058676719666), ('intriguing', 0.6786887645721436), ('thrilling', 0.6741382479667664), ('wonderful', 0.6662275791168213), ('entertaining', 0.6648381948471069), ('terrific', 0.6639219522476196), ('fantastic', 0.6627141833305359), ('exhilarating', 0.6585167646408081), ('enjoyable', 0.6503963470458984)]

问题2.3：同义词和反义词

在考虑余弦相似性时，通常更方便地想到余弦距离，简单来说就是1-余弦相似性

找出三个词$(w_1,w_2,w_3)$，其中$w_1$和$w_2$是同义词，$w_1$和$w_3$是反义词，但余弦距离（$(w_1,w_3)<$余弦距离$(w_1,w_2)$

举个例子，$w_1$ ="happy "与$w_3$ ="sad "比与$w_2$ ="cheerful "更接近。请找到一个满足上述条件的不同例子。一旦你找到了你的例子，请对为什么会出现这种反直觉的结果给出一个可能的解释

您应该在这里使用wv_from_bin.distance(w1, w2)函数来计算两个词之间的余弦距离。请参阅 GenSim documentation以获得进一步的帮助

w1 = "sleep"
w2 = "nap"
w3 = "awake"
w1_w2_dist = wv_from_bin.distance(w1, w2)
w1_w3_dist = wv_from_bin.distance(w1, w3)

print("Synonyms {}, {} have cosine distance: {}".format(w1, w2, w1_w2_dist))
print("Antonyms {}, {} have cosine distance: {}".format(w1, w3, w1_w3_dist))

Synonyms sleep, nap have cosine distance: 0.5380202531814575
Antonyms sleep, awake have cosine distance: 0.42189186811447144

问题2.4：用词向量进行类比

事实证明，词素有时表现出解类比的能力

例如，"男人：国王：：女人：x "的比喻。解读：男人之于王，如同女人之于x），x是什么？

在下面的单元格中，我们向您展示如何使用 GenSim 文档中的 most_similar 函数使用单词向量来查找 x。该函数可以找到与正向列表中的单词最相似的单词，以及与负向列表中的单词最不相似的单词（同时省略输入的单词，这些单词通常是最相似的；参见本文）。类比的答案将具有最高的余弦相似度（最大的返回数值）

让 , , , 和分别表示男人、国王、女人和答案的词向量。只用向量 , , , 以及你的答案中的向量算术运算符 + 和 - ，我们与的余弦相似度最大化的表达式是什么？

提示：回想一下，词向量只是表示一个词的多维向量。用每个向量的任意位置画出一个二维的例子可能会有帮助。男人和女人在坐标平面上相对于国王和答案的位置会在哪里？

pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'king'], negative=['man']))

[('queen', 0.6978678703308105),
 ('princess', 0.6081745028495789),
 ('monarch', 0.5889754891395569),
 ('throne', 0.5775108933448792),
 ('prince', 0.5750998258590698),
 ('elizabeth', 0.5463595986366272),
 ('daughter', 0.5399125814437866),
 ('kingdom', 0.5318052172660828),
 ('mother', 0.5168544054031372),
 ('crown', 0.5164473056793213)]

问题2.5：寻找类比

根据这些向量找到一个类比成立的例子（即目的词排在最前面）。在你的解决方案中请以x:y: : a:b的形式陈述完整的类比。如果你认为这个类比很复杂，请用一两句话解释为什么这个类比成立

注意：你可能要尝试很多类比才能找到有效的类比!
报错：

KeyError: "word 'China' not in vocabulary"
# 再换成France、Canada一样报错
KeyError: "word 'France' not in vocabulary"

解决办法：换成小写（猜测可能是这个训练的模型就是都是小写字母）

pprint.pprint(wv_from_bin.most_similar(positive=['china', 'american'], negative=['america']))

[('chinese', 0.8090777397155762),
 ('beijing', 0.6857120990753174),
 ('taiwanese', 0.6340769529342651),
 ('taiwan', 0.5930265188217163),
 ('shanghai', 0.5679935216903687),
 ('mainland', 0.5571025609970093),
 ('li', 0.5488706231117249),
 ('wang', 0.5484346747398376),
 ('zhang', 0.5481732487678528),
 ('yuan', 0.5459955334663391)]

问题2.6：不正确的类比

根据这些向量找出一个不成立的类比例子。在你的解决方案中，以x:y:: a:b的形式说明所要类比的内容，并根据向量一词说明b的（不正确）值

pprint.pprint(wv_from_bin.most_similar(positive=['china', 'american'], negative=['japan']))

[('chinese', 0.6251887679100037),
 ('u.s.', 0.5653047561645508),
 ('us', 0.5230761766433716),
 ('states', 0.5211377143859863),
 ('americans', 0.5070561170578003),
 ('united', 0.5065516233444214),
 ('cuban', 0.5042911171913147),
 ('and', 0.5031824111938477),
 ('well', 0.4939611554145813),
 ('of', 0.4925920367240906)]

Process finished with exit code 0

问题2.7：引导分析词向量中的偏误

重要的是要认识到我们的词语嵌入中隐含的偏见（性别、种族、性取向等）。偏见可能是危险的，因为它可以通过采用这些模式的应用程序来强化陈规定型观念

运行下面的单元格，检查(a)哪些术语与 "妇女 "和 "工人 "最相似，而与 "男子 "最不相似，以及(b)哪些术语与 "男子 "和 "工人 "最相似，而与 "妇女 "最不相似。指出与女性相关的词语清单和与男性相关的词语清单之间的区别，并解释它是如何反映性别偏见的

pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'boss'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['man', 'boss'], negative=['woman']))

[('bosses', 0.5846002697944641),
 ('girlfriend', 0.5496258735656738),
 ('wife', 0.48936721682548523),
 ('mistress', 0.47348836064338684),
 ('boyfriend', 0.4683174192905426),
 ('tells', 0.46039479970932007),
 ('mother', 0.4581165313720703),
 ('daughter', 0.45619285106658936),
 ('lover', 0.4546445608139038),
 ('husband', 0.44650691747665405)]

[('bosses', 0.5625280141830444),
 ('manager', 0.5502104759216309),
 ('ferguson', 0.49866554141044617),
 ('arsene', 0.4745481014251709),
 ('gambino', 0.4580872058868408),
 ('wenger', 0.45207351446151733),
 ('mourinho', 0.4470241069793701),
 ('tottenham', 0.4417468309402466),
 ('chelsea', 0.43944650888442993),
 ('mafia', 0.43868187069892883)]

问题2.8：词向量的独立分析偏差

使用most_similar函数找到另一种情况，即向量表现出一些偏差。请简要说明你发现的偏误的例子

pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'doctor'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'nurse'], negative=['man']))

[('nurse', 0.6813318729400635),
 ('physician', 0.6672453284263611),
 ('doctors', 0.6173422932624817),
 ('dentist', 0.5775880217552185),
 ('surgeon', 0.5691418647766113),
 ('hospital', 0.564996600151062),
 ('pregnant', 0.5649075508117676),
 ('nurses', 0.5590691566467285),
 ('medical', 0.5542058944702148),
 ('patient', 0.5518484711647034)]

[('nurses', 0.6442357301712036),
 ('pregnant', 0.6110885143280029),
 ('midwife', 0.591461181640625),
 ('mother', 0.5634386539459229),
 ('nursing', 0.5633082389831543),
 ('therapist', 0.554648220539093),
 ('anesthetists', 0.5426579713821411),
 ('anesthetist', 0.5350444316864014),
 ('pediatrician', 0.5249918699264526),
 ('dentist', 0.5185097455978394)]

问题2.9：关于偏差的思考

给出一个解释，说明偏差是如何进入矢量这个词的。你可以做什么实验来测试或测量这种偏差的来源？

关于偏差的理解，一开始就存在于数据集中

小结

第一部分基于计数词向量底层代码编写，相当于在造轮子，实际动手编写一下提取词汇、共现矩阵、降维、绘制word embedding 二维平面图的过程，对于理解NLP早期词向量思想有帮助

第二部分gensim word2vec库入门，这如果真是当作业来写的话肯定有收获的，但没时间，就看看别人写好的代码吧，这次实际上是对上一次官方手册的复习

下一步计划：

• 继续上次的安排，利用gensim的word2vec基于自己找到的中英文语料库进行训练，并达到不错的效果
• CS224n第二次课作业好像需要用到pytorch，到时候可以看一看，好像就是Backprop and Neural Networks，那就没啥