leetcode-106：从中序与后序遍历序列构造二叉树

题目

题目链接

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

解题

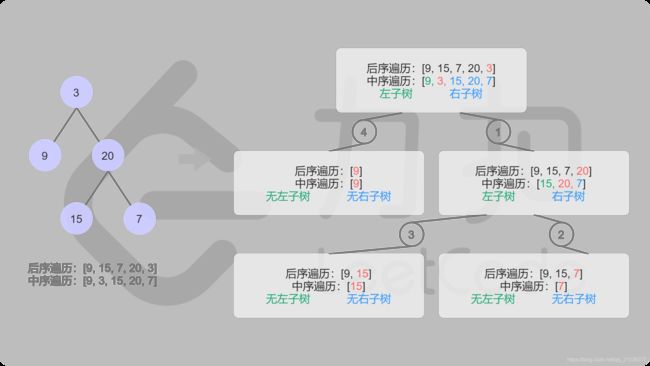
方法一：递归（用4个参数）

和LC-105的一样的方式

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        def MyBuild(postorder_left,postorder_right,inorder_left,inorder_right):
            if postorder_left>postorder_right:
                return None
            postorder_root = postorder_right
            inorder_root = index[postorder[postorder_root]]
            size_left_subtree = inorder_root-inorder_left
            root = TreeNode(postorder[postorder_root])
            root.left = MyBuild(postorder_left,postorder_left+size_left_subtree-1,inorder_left,inorder_root-1)
            root.right = MyBuild(postorder_left+size_left_subtree,postorder_root-1,inorder_root+1,inorder_right)
            return root
        n = len(postorder)
        index = {
     element:i for i,element in enumerate(inorder)}
        return MyBuild(0,n-1,0,n-1)

方法二：递归（用2个参数）

其实就是对上面的方法的一种改进，我们要获得根节点的值，从而从哈希表中找到根节点在中序遍历结果中的索引。
而获得根节点，就没必要像上面那样复杂，只需要从后序遍历结果的最后一个pop出来，就是根节点了。

答案链接

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        def helper(in_left, in_right):
            # 如果这里没有节点构造二叉树了，就结束
            if in_left > in_right:
                return None
            
            # 选择 post_idx 位置的元素作为当前子树根节点
            val = postorder.pop()
            root = TreeNode(val)

            # 根据 root 所在位置分成左右两棵子树
            index = idx_map[val]
 
            # 构造右子树
            root.right = helper(index + 1, in_right)
            # 构造左子树
            root.left = helper(in_left, index - 1)
            return root
        
        # 建立（元素，下标）键值对的哈希表
        idx_map = {
     val:idx for idx, val in enumerate(inorder)} 
        return helper(0, len(inorder) - 1)

特别注意要先构建左子树

root.right = helper(index + 1, in_right)
root.left = helper(in_left, index - 1)

这两个不能换位置。因为postorderpop的结果就是依次是右子树，最后再左子树。
所以这个递归思想，有种深度优先搜索的思想。而方法一，可以换位置(每次递归都相当于处理一个新问题了)，方法二，则都是在postorder.pop()限制下进行，要根据pop的顺序去构建