leetcode 1202.交换字符串中的元素(C/C++/Java/python)
PS:算法并非原创,仅作个人学习记录使用,侵删
题目描述
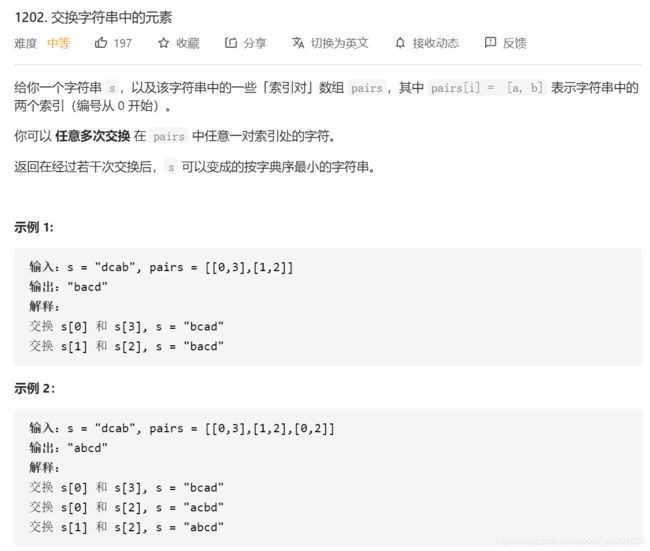
算法分析
阅读完题目之后,我个人没什么具体的思路。穷举法肯定是不行的,因为任意多次交换意味着有无穷种情况,其次我不知道如何才能表示“最小字典序”这个结果要求。
看了一些算法博客的分析以及leetcode官方的题解,这一题可以用三种方式解答:并查集、DFS、BFS,每一种的使用前提都是图论。
这一题和我之前刷到过的一道题的题解方法类似——leetcode 547.省份数量刷题记录
在本题中,建立图的方式是:数组中每个字符作为一个顶点,在pairs数组中出现的一对下标可以看成一种“抽象的边”。这样就能根据已有条件,建立出初始化的图,顶点之间存在相互连接,则称之为“连通分量”。
而本题由于可以随任意多次移动元素,所有连通分量内部有一个性质——顶点之间可以随意交换。因此,一种最常见的算法思路就是:建立图,确认连通分量,每个连通分量之间按照顶点元素的字典序重新排列,得出最后结果。
代码实现
【C】
/*
C语言代码实现思路:并查集,
*/
struct HashTable {
//哈希表结构,每个哈希结构对应一个连通分量
int key;//连通分量小组长
int len;//连通分量的元素个数
int* vec;//连通分量内部顶点之间的联系
UT_hash_handle hh;//使得元素成为hash结构
};
int cmp(int* a, int* b) {
//比较两个元素的大小,用于排序函数
return *b - *a;
}
void swap(int* a, int* b) {
//交换两个元素
int tmp = *a;
*a = *b, *b = tmp;
}
struct DisjointSetUnion {
//联通分量的集合
int *f, *rank;//
int n;//顶点个数
};
void init(struct DisjointSetUnion* obj, int _n) {
//初始化结构体
obj->n = _n;
obj->rank = malloc(sizeof(int) * obj->n);
memset(obj->rank, 0, sizeof(int) * obj->n);
obj->f = malloc(sizeof(int) * obj->n);
for (int i = 0; i < obj->n; i++) {
obj->f[i] = i;
}
}
int find(struct DisjointSetUnion* obj, int x) {
//找到x的父节点
return obj->f[x] == x ? x : (obj->f[x] = find(obj, obj->f[x]));
//返回x或者obj->f[x]
}
void unionSet(struct DisjointSetUnion* obj, int x, int y) {
//合并两个元素代表的集合
int fx = find(obj, x), fy = find(obj, y);
if (fx == fy) {
return;
}
if (obj->rank[fx] < obj->rank[fy]) {
swap(&fx, &fy);
}
obj->rank[fx] += obj->rank[fy];
obj->f[fy] = fx;
}
char* smallestStringWithSwaps(char* s, int** pairs, int pairsSize, int* pairsColSize) {
//s为需要处理的字符数组,pairs为下标对数组,pairsSize为下标对数组大小,pairsColSize为每个下标对的长度
int n = strlen(s);//n为需要处理的字符数组大小,将其视为字符串
struct DisjointSetUnion* dsu = malloc(sizeof(struct DisjointSetUnion));//建立一个并查集结构体
init(dsu, n);//初始化并查集
for (int i = 0; i < pairsSize; i++) {
//对应每个下标对,进行并查集的连通分量合并
unionSet(dsu, pairs[i][0], pairs[i][1]);
}
//至此,并查集的每组连通分量初步构造完成
//之后,进行连通分量的哈希表构建
struct HashTable *mp = NULL, *iter, *tmp;
for (int i = 0; i < n; i++) {
//遍历字符串
int ikey = find(dsu, i);//在并查集中查找第i个元素隶属的小组长
HASH_FIND_INT(mp, &ikey, tmp);//并且在hash表中查找小组长是不是存在
if (tmp == NULL) {
//如果小组长不存在,说明第i个元素代表着一个新的连通分量
tmp = malloc(sizeof(struct HashTable));//构建连通分量的有关信息
tmp->key = ikey;//连通分量的“组长”下标
tmp->len = 1;//连通分量当前已知长度
tmp->vec = NULL;//连通分量的下一个指向元素
HASH_ADD_INT(mp, key, tmp);//将连通分量信息添加进哈希表中,便于后续查找
}
else {
//如果小组长存在,说明第i个元素属于一个已经录入哈希表的联通分量
tmp->len++;//该连通分量元素个数+1
}
}//遍历字符串结束
HASH_ITER(hh, mp, iter, tmp) {
//哈希表遍历
//HASH_ITER(hh, m_pElements, pElement, tmp) 进行哈希表的遍历
iter->vec = malloc(sizeof(int) * iter->len);//连通分量的联系数组根据连通分量长度进行空间开辟
iter->len = 0;//连通分量长度置0
}
for (int i = 0; i < n; i++) {
int ikey = find(dsu, i);//找到第i个元素所在的连通分量“小组长”
HASH_FIND_INT(mp, &ikey, tmp);//在哈希表中查找小组长
tmp->vec[tmp->len++] = s[i];//小组长所在表项存有连通分量长度,该联通分量同样需要更新
}
HASH_ITER(hh, mp, iter, tmp) {
qsort(iter->vec, iter->len, sizeof(int), cmp);//根据字典序大小进行每个连通分量的排序
}
for (int i = 0; i < n; i++) {
//遍历字符串数组
int ikey = find(dsu, i);//每次找连通分量的小组长
HASH_FIND_INT(mp, &ikey, tmp);//找到小组长所在的表项
s[i] = tmp->vec[--tmp->len];//根据排序之后的结果进行结果字符串的更新
}
return s;
}
C语言参考网址
【C++】
/*
C++解题思路:典型的并查集
*/
class UnionFind{
private:
vector<int> parent;//组长结点
vector<int> rank;//表示并查集之间的联系
public:
UnionFind(int n){
//并查集的建立和初始化
parent.resize(n);
rank.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
rank[i]=1;
}
}
void Union(int x,int y){
//合并两的元素代表的集合
int x_root=Find(x);
int y_root=Find(y);
if(rank[x_root]==rank[y_root]){
parent[x_root]=y_root;
rank[y_root]++;
}
else if(rank[x_root]<rank[y_root]){
parent[x_root]=y_root;
}
else{
parent[y_root]=x_root;
}
}
int Find(int x){
//并查集中是不是能找到元素的连通分量小组长
if(x!=parent[x]){
x=Find(parent[x]);
}
return x;
}
};
class Solution {
public:
string smallestStringWithSwaps(string s, vector<vector<int>>& pairs) {
if(s.length()==0){
//特殊情况
return 0;
}
int len=s.length();
UnionFind unionFind(len);//建立并查集并初始化,初始时,每个顶点表示单独的连通分量
for(vector<int>& pair:pairs){
//遍历pairs数组
unionFind.Union(pair[0],pair[1]);//根据pairs内容合并连通分量
}
//这里采用优先队列进行储存环里的元素,自动排序
unordered_map<int,priority_queue<char,vector<char>,greater<char>>> hashtable;
for(int i=0;i<len;i++){
//遍历待处理数组
int root=unionFind.Find(i); //找到该元素对应的根
hashtable[root].push(s[i]); //将该元素放入对应的根里
}
string res;//结果字符串
for(int i=0;i<len;i++){
//获取结果字符串
int root=unionFind.Find(i);
res+=hashtable[root].top();
hashtable[root].pop();
}
return res;
}
};
C++参考网址
【java】
/*
java解题思想:
先根据索引对集合将索引合并,这样可任意交换的索引同处一个连通分量。由于字符串每个索引位置的字符都应取该索引对应连通分量中的字典序的最小值,因此构建一个哈希表,其键值为索引对应连通分量的根节点(代表元),值为同一个连通分量的字符集合,使用优先队列维护字典序。这样构建字符串时取每个索引对应的连通分量中字符集合的最小字符即可。下面代码在构建并查集时使用了按秩压缩和完全路径压缩的技巧
*/
class Solution {
public String smallestStringWithSwaps(String s, List<List<Integer>> pairs) {
if (pairs.size() == 0) return s;
int len = s.length();
UnioFind unionFind = new UnioFind(len);
for (List<Integer> pair : pairs) {
int index1 = pair.get(0);
int index2 = pair.get(1);
unionFind.union(index1, index2);
}
char[] arr = s.toCharArray();
// key 为每一个索引所在连通分量的代表元 values: 同一个连通分量的字符集合
Map<Integer, PriorityQueue<Character>> hashMap = new HashMap<>(len);
for (int i = 0; i < len; i++) {
int root = unionFind.find(i);
if (hashMap.containsKey(root)) {
hashMap.get(root).offer(arr[i]);
} else {
PriorityQueue<Character> queue = new PriorityQueue<>();
queue.offer(arr[i]);
hashMap.put(root, queue);
}
}
StringBuilder bd = new StringBuilder();
for (int i = 0; i < len; i++) {
int root = unionFind.find(i);
bd.append(hashMap.get(root).poll());
}
return bd.toString();
}
private class UnioFind {
private int[] parent;
/**
* 以i为根节点的子树的高度(引入了路径压缩以后该定义并不明确)
*/
private int[] rank;
public UnioFind(int n) {
this.parent = new int[n];
this.rank = new int[n];
for (int i = 0; i < n; i++) {
this.parent[i] = i;
this.rank[i] = 1;
}
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY)
return;
if (rank[rootX] == rank[rootY]) {
parent[rootX] = rootY;
// 此时以rootY为根节点的树的高度增加了 1
rank[rootY] += 1;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
// 此时以rootY为根结点的树的高度不变
} else {
parent[rootY] = rootX;
// 同理以rootX为根结点的树的高度不变
}
}
// 完全路径压缩
public int find(int x) {
if (x != parent[x]) {
parent[x] = find(parent[x]);
}
return parent[x];
}
}
}
Java参考网址
【python】
#
#python解题思路:
#深度优先遍历——DFS
#
class Solution:
def dfs(self,res,graph,visited,x):#深度优先遍历
for neighbor in graph[x]:
if not visited[neighbor]:
visited[neighbor] = 1
res.append(neighbor)
self.dfs(res,graph,visited,neighbor)
def smallestStringWithSwaps(self, s, pairs):
# 建图
graph = [[] for _ in range(len(s))]
visited = [0] * len(s)
for x,y in pairs:
graph[x].append(y)
graph[y].append(x)
res = list(s)
for i in range(len(s)):
if not visited[i]:
# 获取连通节点
connected_nodes = []
self.dfs(connected_nodes,graph,visited,i)
# 重新赋值
indices = sorted(connected_nodes)
string = sorted(res[node] for node in connected_nodes)
for j,ch in zip(indices,string):
res[j] = ch
return "".join(res)
python参考网址