LeetCode之位运算
LeetCode中关于位运算的题目。
0. 原理
- 基本原理
0s 表示一串 0,1s 表示一串 1。
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
- 利用 x ^ 1s = ~x 的特点,可以将一个数的位级表示翻转;
- 利用 x ^ x = 0 的特点,可以将三个数中重复的两个数去除,只留下另一个数。
1 ^ 1 ^ 2 = 2
- 掩码操作
利用 x & 0s = 0 和 x & 1s = x 的特点,可以实现掩码操作。
一个数 num 与 mask:00111100 进行位与操作,只保留 num 中与 mask 的 1 部分相对应的位。
01011011 &
00111100
--------
00011000
- 设值操作
利用 x | 0s = x 和 x | 1s = 1s 的特点,可以实现设值操作。
- 一个数 num 与 mask:00111100 进行位或操作,将 num 中与 mask 的 1 部分相对应的位都设置为 1。
01011011 |
00111100
--------
01111111
- 算法常用操作 n & (n-1)
这个操作是算法中常见的,作用是消除数字 n 的二进制表示中的最后一个 1。
看个图就很容易理解了:
- 算法常用操作 n & (-n)
n&(-n) 得到 n 的位级表示中最低的那一位 1。-n 得到 n 的反码加 1,也就是 -n=~n+1。例如对于二进制表示 10110100,-n 得到 01001100,相与得到 00000100。
10110100 &
01001100
--------
00000100
n-(n&(-n)) 则可以去除 n 的位级表示中最低的那一位 1,和 n&(n-1) 效果一样。
- 移位运算
>> n 为算术右移,相当于除以 2n,例如 -7 >> 2 = -2。
11111111111111111111111111111001 >> 2
--------
11111111111111111111111111111110
<< n 为算术左移,相当于乘以 2n。-7 << 2 = -28。
11111111111111111111111111111001 << 2
--------
11111111111111111111111111100100
- mask 计算
要获取 111111111,将 0 取反即可,~0。
要得到只有第 i 位为 1 的 mask,将 1 向左移动 i-1 位即可,1<<(i-1) 。例如 1<<4 得到只有第 5 位为 1 的 mask :00010000。
要得到 1 到 i 位为 1 的 mask,(1< 要得到 1 到 i 位为 0 的 mask,只需将 1 到 i 位为 1 的 mask 取反,即 ~((1< 两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。 给出两个整数 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 两个相同的数异或的结果为 0,对所有数进行异或操作,最后的结果就是单独出现的那个数。 给定一个包含 将数组中的元素与 给定一个整数数组 将所有元素进行异或运算,得到两个不重复元素的异或值,也就是这两个元素中不相同的部分为1 的数, 颠倒给定的 32 位无符号整数的二进制位。 利用相同数异或为 0 。 给定一个整数,编写一个函数来判断它是否是 2 的幂次方。 如果一个数为 2 的 n 次方,则说明这个数的二进制形式只包含一个 1,利用 给定一个整数 (32 位有符号整数),请编写一个函数来判断它是否是 4 的幂次方。 这种数在二进制表示中有且只有一个奇数位为 1,例如 16 (10000)。 给定一个正整数,检查他是否为交替位二进制数:换句话说,就是他的二进制数相邻的两个位数永不相等。 对于 1010 这种位级表示的数,把它向右移动 1 位得到 101,这两个数每个位都不同,因此异或得到的结果为 1111,通过 给定一个正整数,输出它的补数。补数是对该数的二进制表示取反。 不使用运算符 a ^ b 表示没有考虑进位的情况下两数的和,(a & b) << 1 就是进位。 给定一个字符串数组 给定一个非负整数 num。对于 对于数字 1. 统计两个数的二进制表示有多少位不同
x 和 y,计算它们之间的汉明距离。输入: x = 1, y = 4
输出: 2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
(z % 2) 或者与运算 (z & 1)。class Solution:
def hammingDistance(self, x: int, y: int) -> int:
z = x ^ y
ans = 0
while z != 0:
if (z & 1) == 1:
ans += 1
z = z >> 1
return ans
z & (z-1) 去除 z 位级表示最低的那一位。 def hammingDistance(self, x: int, y: int) -> int:
z = x ^ y
ans = 0
while z != 0:
z = z & (z - 1)
ans += 1
return ans
2. 数组中唯一一个不重复的元素
输入: [4,1,2,1,2]
输出: 4
class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for num in nums:
res = res ^ num
return res
3. 找出数组中缺失的那个数
0, 1, 2, ..., n 中 n 个数的序列,找出 0 .. *n* 中没有出现在序列中的那个数。输入: [9,6,4,2,3,5,7,0,1]
输出: 8
0..n 中的每个元素进行异或,由于相同的元素异或为 0, 最后得到就是没有出现在序列中的那个数。class Solution:
def missingNumber(self, nums: List[int]) -> int:
res = 0
for i in range(len(nums)):
res = res ^ i ^ nums[i]
return res ^ len(nums)
4. 数组中不重复的两个元素
nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。输入: [1,2,1,3,2,5]
输出: [3,5]
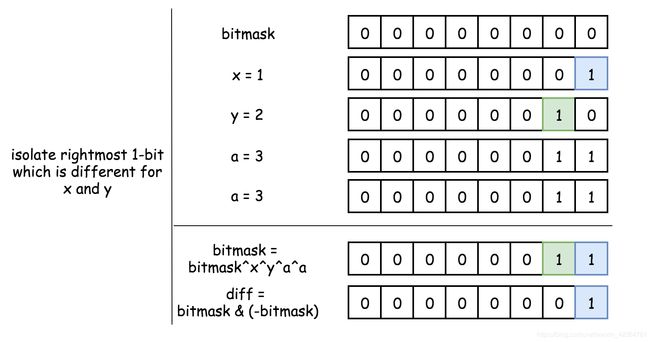
n & (-n)得到 n 的位级表示中最低的那一位 1,这个 1 只可能来自两个不重复元素中的一个 (就算重复数的二进制数中也有可能包含这个 1,但通过 x ^= num 的异或操作便消除)。class Solution:
def singleNumber(self, nums: int) -> List[int]:
# difference between two numbers (x and y) which were seen only once
bitmask = 0
for num in nums:
bitmask ^= num
# rightmost 1-bit diff between x and y
diff = bitmask & (-bitmask)
x = 0
for num in nums:
# bitmask which will contain only x
if num & diff:
x ^= num
return [x, bitmask^x]
5. 反转一个数的比特数
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
n >> 1(n & 1) << powern == 0 时,迭代终止class Solution:
def reverseBits(self, n: int) -> int:
res = 0
power = 31
while n:
res += (n & 1) << power
n >>= 1
power -= 1
return res
6. 不适用额外变量交换两个整数
a = a ^ b
b = a ^ b
a = a ^ b
7. 判断一个数是不是 2 的 n 次方
输入: 1
输出: true
解释: 20 = 1
n & (n - 1) 去除最低的一位 1,也就是次数中唯一的一个 1,去除之后为 0。class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return n > 0 and n & (n - 1) == 0
8. 判断一个数是不是 4 的 n 次方
输入: 16
输出: true
class Solution:
def isPowerOfFour(self, num: int) -> bool:
return num > 0 and num & (num - 1) == 0 and (num & 0b01010101010101010101010101010101) != 0
9. 判断一个数的位级表示是否不会出现连续的 0 和 1
输入: 5
输出: True
解释:
5的二进制数是: 101
temp & (temp + 1) 是否为 0 可以判断异或的结果是否为全 1。class Solution:
def hasAlternatingBits(self, n: int) -> bool:
temp = n ^ (n >> 1)
return temp & (temp + 1) == 0
10. 求一个数的补码
输入: 5
输出: 2
解释: 5 的二进制表示为 101(没有前导零位),其补数为 010。所以你需要输出 2 。
class Solution:
def findComplement(self, num: int) -> int:
if num == 0: return 1
mask = 1 << 30
while num & mask == 0:
mask >>= 1 # 找到原数中最左边的 1
mask = (mask << 1) - 1 # 得到掩码
return num ^ mask
11. 实现整数的加法
+ 和 - ,计算两整数 a 、b 之和。输入: a = 1, b = 2
输出: 3
class Solution:
def getSum(self, a: int, b: int) -> int:
a &= 0xFFFFFFFF
b &= 0xFFFFFFFF
while b:
carry = a & b
a ^= b
b = ((carry) << 1) & 0xFFFFFFFF # 模拟溢出操作
return a if a < 0x80000000 else ~(a^0xFFFFFFFF)
12. 字符串数组最大乘积
words,找到 len(word[i]) * len(word[j]) 的最大值,并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词,返回 0。输入: ["abcw","baz","foo","bar","xtfn","abcdef"]
输出: 16
解释: 这两个单词为 "abcw", "xtfn"。
n = ord(ch) - ord('a'),然后创建一个第 n 位为 1 的掩码 nth_bit = 1 << n,通过或操作将该码合并到位掩码中 bitmask |= nth_bit。class Solution:
def maxProduct(self, words: List[str]) -> int:
n = len(words)
masks = [0] * n # 记录每个单词的掩码
lens = [0] * n # 记录每个单词的长度
bit_number = lambda ch : ord(ch) - ord('a')
for i in range(n):
bitmask = 0
for ch in words[i]:
# add bit number bit_number in bitmask
bitmask |= 1 << bit_number(ch) # 得到每个单词的掩码
masks[i] = bitmask
lens[i] = len(words[i])
max_val = 0
for i in range(n):
for j in range(i + 1, n):
if masks[i] & masks[j] == 0: # 与运算为 0,说明两个字符串没有重复字母
max_val = max(max_val, lens[i] * lens[j])
return max_val
13. 统计从 0~n 每个数的二进制表示中 1 的个数
0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。输入: 5
输出: [0,1,1,2,1,2]
0,1,2,3,4,5
6 (110),它可以看成是 4 (100) 再加一个 2 (10),因此 dp[i] = dp[i & (i-1)] + 1; 即数字 i & (i-1) 相对于数字 i 来说,只是缺少了最后的一个 1,加上 1 即为 i 中 1 的个数。class Solution:
def countBits(self, num: int) -> List[int]:
res = [0] * (num + 1)
for i in range(1, num + 1):
res[i] = res[i & (i - 1)] + 1
return res