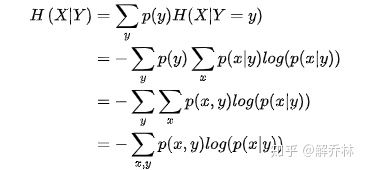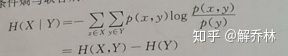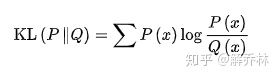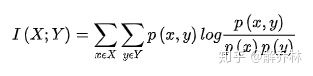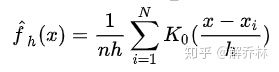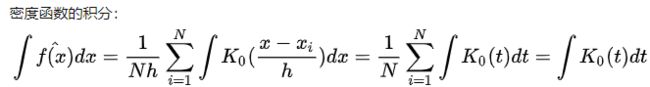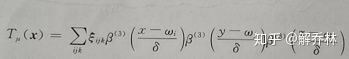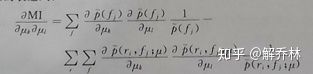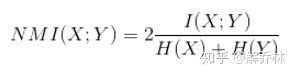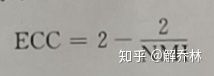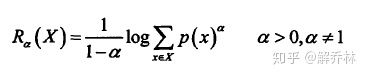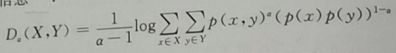python 图像刚性变换_（十）基于信息论的医学图像配准（传统）

• 一开始，信息论是专门研究信息的有效处理以及可靠传输的一门科学。香农首次对信息论建立了数学模型，现在，信息论已经渗透到图像处理中，本小结就是研究互信息在医学图像配准中 的应用。并描述了几种关于信息论的处理方法
• 互信息的值并不是一个闭区间，优化函数多峰，容易陷入局部最优点。

1）信息论基础概念

1、熵是什么？

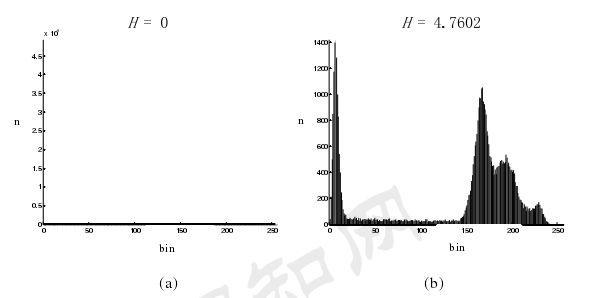
熵是表示分子的 混乱程度。越是混乱，熵越大。一开始熵是来源于物理学，后被香农量化到信息论中，表示信源的不确定程度。一般利用灰度直方图来统计像素灰度值的概率分布情况

2、香农熵：

（X表示离散的随机变量，p（x）表示离散的随机函数）

例子：

如上图：灰度级别越分散，灰度越分散，熵越大。

香农熵的性质：非负、凸、对称、具有极值性

3、联合熵和条件熵

注：如果把熵的概念扩展到一对随机变量中，他是衡量一对随机变量所包含的信息量，换句话说就是这两个变量的相似程度！！！

4、条件熵、边缘熵、联合熵之间的关系

例子：下面的图b-e是原始图像旋转10、20、30的联合灰度直方图分布

越不匹配，对应的联合灰度直方图越复杂。

5、互信息

1）互信息与联合熵

互信息通常用来描述两个图像之间的统计相相关性，通常用 I 表示

理论上，联合熵和互信息是类似的，描述图像的统计相关性，都可以敏感出图像之间的相关关系，图像的互信息和联合熵都可以作为一种配准测度。但是互信息针对两幅图像严重不i配是，引入了边缘熵，这个时候不会像联合熵一样产生错误配准的问题。

相对熵表示的是两个随机变量间距离的一种度量D，而互信息表示的是一对随机变量包含另一个随机变量之间的程度I，当两个实际变量相等时，D=0，I=1,公式如下：

互信息与边缘熵、条件熵、联合熵之间的关系

2、互信息在图像配准中的应用

不同模态的图像，他的相同目标的灰度可能不同，但是他的组织、器官，灰度值对应的三维空间相同位置是相同的-统计相关的。

把互信息作为配准测度，两幅共同解刨的结构的图像配准最好时，互信息达到最大。

2.1、图像互信息【只有将图片灰度转化为概率密度时，才可以用其目标公式】

如果把图像的灰度值作为随机变量，引入互信息，这个时候，我们就可以利用其定理衡量图像

步骤：

• 图像的边缘概率-利用直方图估计
• 图像的联合概率-利用联合直方图估计
• 概率分布估计

参数估计（假设每一类概率密度已知，参数未知，这个时候利用贝叶斯、最大似然估计）； 非参数估计：利用直方图、核密度、K临近

2.2、概率密度估计【只有将图片灰度转化为概率密度时，才可以用其目标公式】

• 直方图估计（快、简单；但是只能估计离散的分布）
• 核密度估计（能估计连续概率分布，用于非刚性配准）

1）直方图估计：

简单来说就是参考图像与浮动图像，各自关于灰度划分n，m个区间，统计每个点的灰度落在那个区间，通过它可以了解到各个点的灰度情况以及分布是否均匀或者分布在那个区间内。

但是直方图估计会导致信息的丢失，并且他不是唯一的，也不是平滑的，而且无极值

2）核密度估计（帕曾窗估计）的原理：

利用核密度对样本进行平滑，使得得到连续的概率密度函数

他是基于样本平滑的、样本来估计总体概率密度函数（核密度估计其实是对直方图的一个自然拓展。）

通过上面公式，大家也能看出，其实核密度估计就是对直方图的一个扩展，或者说是平滑，他的要求只有一个，就是这个函数的积分为1。

书上提到了4种常用的核密度函数

矩函数，三角核函数，高斯核函数以及一二三阶B样条函数

注：B样条它能够很好的用于用于非刚性配准

3、基于互信息的医学图像配准

核心：将互信息作为衡量待配准图像的相似度

首先：图像配准可以看成是寻找两个图片的最优空间变换的过程

算法公式化【目标函数】

注：argmax表示的是当μ取到何值时，使得后面的式子最大，MI（）表示参考图像与浮动图像之间的互信息，R（x,y,z）表示参考图像，F（Tμ（x,y,z））表示浮动图像，这个Tμ表示对x,y,z的转换，如果不是整数，一般是用 插值（）的方法

上述就是目标公式

4、我们具体化配准算法流程：

• 1、空间变换【搜索空间】--FFD

根据前面的基础知识可知，空间变换分为：刚性变换、仿射变换投影变换，弯曲变换(弹性形变)弯曲变换-自由形态形变（FFD）+B样条函数性能较好

基于B样条的，自由形态形变模型用于建模图像间的局部形变是非常好的

步骤：

• 1、为了提高效率，先用全局变换对图像进行粗配准
• 2、变：Tμ，利用网格以及三阶B样条（平滑）的线性结合

上面的

表示网格与控制点的控制矢量，

表示各个方向上的控制点，

表示网格的间隔。这个时候，我们就可以通过网格法以及三阶B样条（用于平滑），进行配准了

• 2、配准模型的求解（增量与方向）【搜索策略】--L-BFGS

我们需要优化算法求出下述目标函数的极值

根据上述优化算法的介绍，我们发现牛顿法比梯度法更好的收敛，但是牛顿法要求海森矩阵的逆，非常的复杂，提出了伪牛顿法BFGS，我们自己更改，L-BFGS为伪牛顿法的变种（就是在有限的空间内的BFGS）

泰勒公式：

μ表示其增量，进行迭代

迭代过程，H表示每一步的步长，是海森矩阵逆的估计

n表示空间变换的参数的个数，刚性全局变换，参数为6个，非刚性变换，参数是看网格的大小。

• 3、【相似性度量】--互信息

1、概率密度估计（互信息以及相似度度量的基础）

为了保证概率的鲁棒性，需要计算相似度的解析导数，通过核函数估计连续的概率密度函数【直方图估计是只能估计离散的核函数】

一般用0阶B样条函数来估计参考图像的概率密度函数

参考图像的概率密度函数：

浮动图像的概率密度函数：

联合密度函数：

条件密度函数：

注：R°，F°表示图像的灰度的最小值，

b表示箱宽。

他的值代表着参考图像和浮动图像之间的差距==灰度差距

2、互信息求导（求其精确度）【相似性度量】--互信息

这个时候，我们把前面的概率密度函数等全部带入到

后，对其求极值，就能够得到μ何时时，下面的目标函数最大了

对其求导：

这样，我们就完成了任务。我们来梳理一下算法流程：

互信息并不是直接的对图像的灰度值进行衡量其一致性，而是量化待配准图形的概率分布之间的相关性，使用优化的方法使得图像的互信息达到最大值的空间变换，是指精确配准。

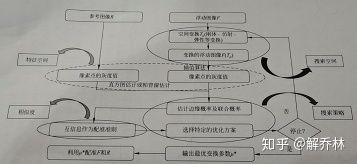
流程概述

解析流程：

针对目标函数的求解过程

首先，对浮动图像通过空间变换，变为F(Tμ)【搜索空间】，利用差值算法，得到浮动图像的灰度值，对参考图像进行灰度值计算，通过直方图或者帕曾窗估计对参考图形、浮动图像的像素点的灰度值进行估计。【特征空间】，对浮动图像估计边缘密度、联合密度，与参考图像进行互信息配准，选定优化方案【相似度度量】，当达到一定的步数，或者μ的临近两次差值足够的小的时候，输出最优变换μ【搜索策略】，并且利用μ※对参考图像以及浮动图像进行配准。

5、几种基于信息论的相似性度量方法【对香农熵的一种优化】

归一化度量【NMI】（解决了互信息对图像重叠问题的敏感度问题）

熵相关度量【ECC】（类似于归一化）

互累计剩余熵【CCRE】（具有更广泛的性质，将概率分布转化为累计概率分布问题）

Alpha互信息【A-MI】（推广）

詹森瑞利散度【JRD】（互信息的另外一种形式，利用詹森不等式和香农熵构造的一种散度）

---