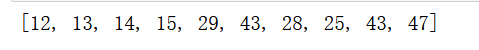python-OpenCV：模糊操作，高斯模糊，原理及其代码解析。

系列文章目录

本文针对模糊操作由浅入深做原理及代码解析。

---

---

模糊

模糊是什么

在学习之前，必须要清楚的是模糊是什么？说得最直观一点就是，假设一个人是600度的近视，他离另一个人2米时，戴眼镜时看到的图像转化到不戴眼镜时看到的图像就是模糊的过程。
但是在计算机视觉领域，我们不能从人的感观来说。
模糊，属于低通滤波的一种，它称为模糊，也可以称为平滑。
低通滤波是一种信号过滤方式，指的是低频率的信号可以通过，而超过设定界限的信号会被阻断，减弱等等。
从直观来看：
右图至左图的操作就叫模糊。

模糊操作的原理

对一个图像来说，从OpenCV角度分析，它无非就是一个三维的矩阵，每一维的每一个元素，代表在这个色彩维度的亮度，那么我们不难想象，对于一张图像而言，如果两个像素点的数值大小处于极大极小的极端，那么对比就会很明显，比如255和0，白和黑一眼分明，但是如果很相近，比如122和123那么就很像，换句话来说，这块的图像就很平滑。模糊操作其实就是让图像变得很平滑，一旦很平滑，那么图像就会失去原先的棱角分明，所以看着就没有原先的清楚。那么实现的话其实也没有很困难是吧，最简单的实现，就是我们从最开始的像素点开始两个两个遍历，并不断的赋予均值，对每个像素点进行改变，但是那种模糊已经让图像失去了原先的价值，所以OpenCV内部提供的模糊操作API远远没有那么简单。但是这种模糊方式作为原理介绍就很容易明白。

基于离散卷积的模糊

图像的卷积操作：卷积这个概念应该在深度学习中比较好理解。我们可以举个简单的例子来说说。另外，这里我们需要谨记一句话：对图像来说，越卷越平滑。
对如下一行数据做卷积
我们给定卷积核为2的1*3的矩阵如下
卷积过程如下：
对于第一个数据和最后一个数据，直接就保留原数据，卷积核从第二个数据开始计算。
用代码算：

a_list=[12,13,15,15,16,71,14,15,56,47]
b=[1,2,1]
c_list=[12]
for i in range(1,9):
    c_list.append((b[0]*a_list[i-1]+b[1]*a_list[i]+b[2]*a_list[i+1])//4)
c_list.append(47)
print(c_list)

对于像素点的卷积计算只需要泛化到相应的维度就可以了，这里就不细说了，原理大概明白就够了。ok，接下来直接调用API看效果。

均值模糊

均值模糊：对邻近选定的像素点做卷积，求均值。

import cv2 as cv
import numpy as np

#均值模糊 使图片模糊
def get_mean_burry(image):
    cv.imshow('iamge',image)
    dst=cv.blur(image,(5,5))
    cv.imshow('burry',dst)



src=cv.imread('ky_1.jpg')
get_mean_burry(src)
cv.waitKey(0)
cv.destroyAllWindows()

结果如下：
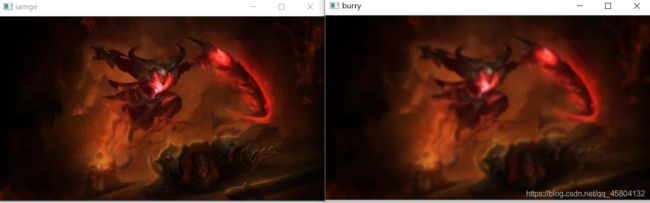重点方法解析：dst=cv.blur(image,(5,5))

cv2.blur(image,kernel_size)
image:原图
kernel_size:卷积核尺寸

这里如果假设为33，其实就是一个，那么55也很容易想的来

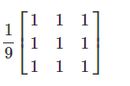
这样的矩阵，通过前面的知识，相同的算法，可以重新计算出一些简单图片的像素点做对比。

中值模糊

中值模糊，其实就是选定一个范围内的像素点，排序后选出中值，之后填入中心像素点中。借知乎的图：鸣谢

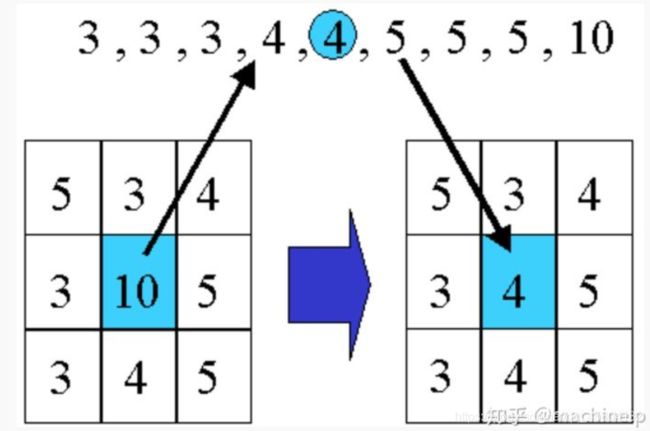
代码如下;

import cv2 as cv
import numpy as np

#中值模糊可以抹除椒盐噪点。
def get_mid_blurry(image):
    cv.imshow('noise',image)
    dst=cv.medianBlur(image,5)
    cv.imshow('no_noise',dst)


src=cv.imread('ky_1.jpg')
get_mid_blurry(src)
cv.waitKey(0)
cv.destroyAllWindows()

cv.medianBlur(image,5),参数很容易解释：image为原图，5表示选取邻域的大小，这里指的是以该像素点为中心5为边长的正方形。所以这里的参数为奇数。

自定义模糊

代码：

import cv2 as cv
import numpy as np


#自定义模糊
def get_customer_burry(image):
    #定义卷积核，算子
    #该方法与均值模糊 5*5的卷积类似
    #kernel=np.ones([5,5],np.uint32)/25
    #kernel=np.array([[1,1,1],[1,1,1],[1,1,1]],np.float32)/9
    #image=np.float32(image)
    #卷积的锐化算子
    kernel=np.array([[0,-1,0],[-1,5,-1],[0,-1,0]],np.float32)
    dist=cv.filter2D(image,-1,kernel=kernel)
    cv.imshow('customer',dist)

cv2.filter2D():使用自定义内核对图像进行卷积，它不仅可以让图像变得模糊，还可以让图像变得更锐化。该方法的使用花样很多，这里不细说，-1参数代表所需要的的深度，这里是默认。kernel表示卷积核。可以记住这种方法，一般的模糊和锐化不会改动其他地方，最大的改动应该就是自己定义的卷积核，这里几种都写在代码里面了。

高斯模糊（重点）

高斯模糊属于均值模糊的一种，可以说是一种特殊的均值模糊，虽然它的名字听上去有点恐怖，但是实际上高斯模糊是一种没有很难的数学算法。其实说白了它的操作只有几步：利用高斯分布求高斯掩膜，之后利用高斯掩膜操作图像。这里我们需要从高斯分布开始说起。

高斯分布是概率论中的内容，可能有一些伙伴学习过概率论，当然可有一些朋友没有学过概率论，不过无所谓。

高斯分布

高斯分布又称正态分布。如下为高斯分布概率分布图。以及高斯分布的计算公式

μ指均值，σ指标准差，当μ=0，σ=1时为标准正态分布，公式如下：

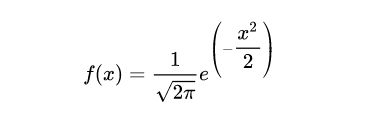
高斯模糊

而我们要做的高斯模糊，其实是通过一个高维的高斯分布计算高斯掩膜的，而且是在基于μ=0的基础上做的，因为，每次计算都要从选定像素点计算，因此可以直接忽略μ，我们从简单一维的角度分析对如下的坐标。

做向量计算(x1-x2) ^2+(y1-y2) ^2并求平方2，得到。

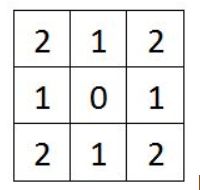
令σ为1，取高斯分布的值。
如下：

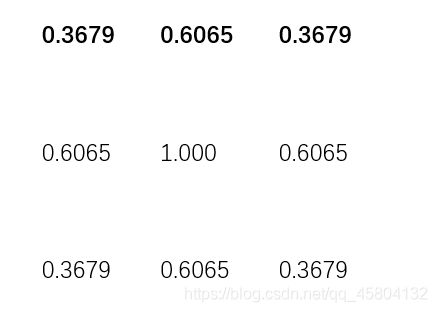
之后对表格进行归一化，即同除以之和。

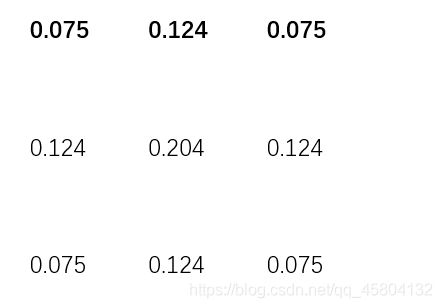
这就是所谓的高斯掩膜了，高斯掩膜只与σ有关，关于证明的话，有兴趣的话小伙伴可以自己动手算一下，它与xy是没有关系的，因为xy会被抵消的。
接下来我们看代码：

#加载图像 利用循环遍历加载高斯噪声 利用API去除高斯噪声  代码方面应该差不多了，接下里是原理及博客了。
import cv2 as cv 
import numpy as np

#加载图像
def load_image():
    src=cv.imread('ky_2.jpg')
    return src
#处理超限
def clip(num):
    if num>255:
        return 255
    elif num<0:
        return 0
    else:
        return num
#放置高斯噪声
def gaussian_image(image):
    h,w,ch=image.shape
    for i in range(h):
        for j in range(w):
            #随机矩阵 1*3
            s=np.random.normal(0,20,3)
            image[i,j,0]=clip(image[i,j,0]+s[0])#blue
            image[i,j,1]=clip(image[i,j,1]+s[1])#green
            image[i,j,2]=clip(image[i,j,2]+s[2])#red
    return image
#利用API去噪
def clear_noise(image):
    dst=cv.GaussianBlur(image,(3,3),2,2)
    return dst
#展示
def show_and_time():
    src=load_image()
    cv.imshow('image',src)
    t_1=cv.getTickCount()
    noise=gaussian_image(src)
    cv.imshow('noise',noise)
    dst=clear_noise(noise)
    cv.imshow('dst',dst)
    t_2=cv.getTickCount()
    print('time {0:.2f} ms'.format((t_2-t_1)/cv.getTickFrequency()*1000))
    cv.waitKey(0)
    cv.destroyAllWindows()

    
    
show_and_time()

• numpy.random产生随机矩阵。
• 两个计时函数，之前的博客写到过，这里是提一下。
• 对超出范围的数字要做处理，否则会出问题。

numpy.clip方法，可以代替如下的控制范围的函数，并且clip方法是用向量计算，因此效率更高，可替换为np.clip(x,0,255)效果为对于x向量中所有的元素，控制在0~255范围之间。
重点方法：cv.GaussianBlur(image,(3,3),2,2)

cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]]) → dst

src为原图。这里的第一个2是sigmoidX，第二个2是sigmoidY，他们的作用是产生两个一维的卷积核在行和列处做卷积。(3,3)为卷积核尺寸，上面已经解释过。效果如下：