C++排序算法实现(更新中)
比较排序法:如冒泡排序、简单选择排序、合并排序、快速排序。其最优的时间复杂度为O(nlogn)。
其他排序法:如桶排序、基数排序等。时间复杂度可以达到O(n)。但试用范围有要求。
桶排序:排序的数组元素跨距不能很大。因为跨距很大的话,会开辟大量的内存。
基数排序:只适用于整数。

图片来自博客:
https://www.cnblogs.com/wuxiangli/p/6399266.html
排序的稳定性
考察排序算法的时候有一个很重要的特性,就是算法的稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri=rj,且ri在rj之前,而在排序后的序列中,ri仍在rj之前,则称这种排序算法是稳定的;否则称为不稳定的。
1、冒泡排序(O(n2))
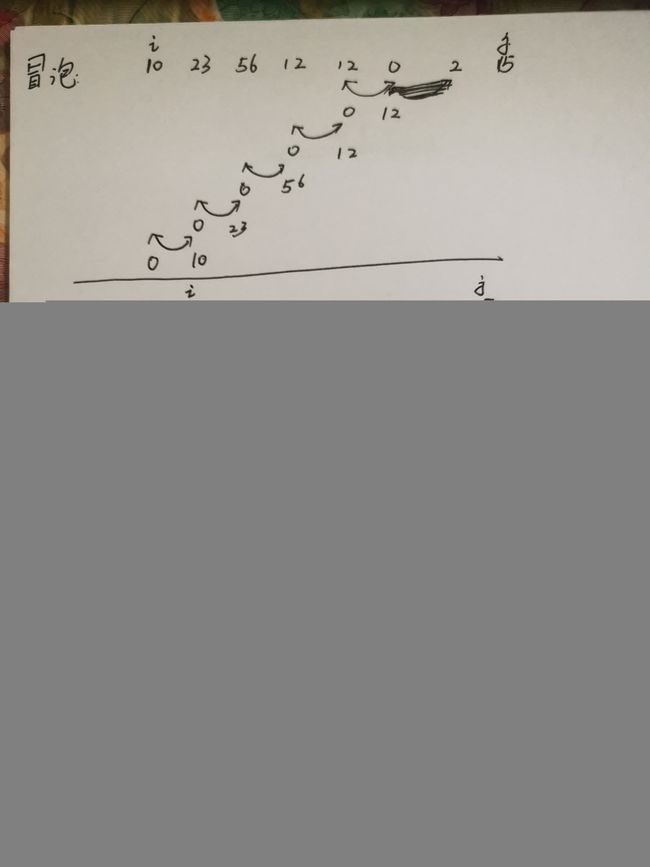
1.1、普通冒泡排序
void print_array(int* a)
{
for(int i = 0;i<8;i++)
cout<<a[i]<<" ";
cout<<endl;
}
int main()
{
int a[8] = {
10,23,56,12,12,0,2,15};
for(int i = 0;i<8;i++)
{
for (int j = 7; j > i; j--)
{
if(a[j] < a[j-1])
{
int temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
}
print_array(a);
}
}
1.2、带标记为的冒泡排序
如果在某次冒泡的过程中,没有发生数据交换,说明已经排好序了,没有必要继续进行。因此可以设置一个标志位:bool flag。
void print_array(int* a)
{
for(int i = 0;i<8;i++)
cout<<a[i]<<" ";
cout<<endl;
}
int main()
{
int a[8] = {
10,23,56,12,12,0,2,15};
bool flag = true;
for(int i = 0;i<8 && flag;i++)
{
// 如果以后没有数据交换,flag就会是false
flag = false;
for (int j = 7; j > i; j--)
{
if(a[j] < a[j-1])
{
// 发生数据交换时,标志位置为true。
flag = true;
int temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
}
}
print_array(a);
}
}
2、简单选择排序(O(n2))
从第一位开始,每次选择最小的数据,和开始时的数据进行交换。
void print_array(int* a)
{
for(int i = 0;i<8;i++)
cout<<a[i]<<" ";
cout<<endl;
}
int main()
{
int a[8] = {
10,23,56,12,12,0,2,15};
for(int i = 0;i<7;i++)
{
int min = i;
for(int j = i+1;j<8;j++)
{
if(a[j] < a[min])
min = j;
}
if(min != i)
{
int temp = a[min];
a[min] = a[i];
a[i] = temp;
}
}
print_array(a);
}
3、归并排序(nlogn)
归并排序的思路为:将数组不断的分为两部分。如一个长度为8的数组—>长度为4—>长度为2—>长度为1。然后再两两合并。在合并的过程中,数组已经有序了,因此时间复杂度会降低。

// 合并两个数组的函数
void Merge(int* a,int left1,int right1,int left2,int right2)
{
// 由于后面会用到left1,left2的原值,因此这里先备份一个。
int temp_left1 = left1;
int temp_left2 = left2;
int n = (right1 - left1 + 1) + (right2 - left2 + 1);
vector<int> result;
// 此时两个数组已经是有序的,合并的过程中,有一个数组到头后就停止
while(left1 <= right1 && left2 <= right2)
{
if(a[left1] <= a[left2])
result.push_back(a[left1++]);
else
result.push_back(a[left2++]);
}
// 遍历剩下的部分
while(left1 <= right1)
result.push_back(a[left1++]);
while(left2 <= right2)
result.push_back(a[left2++]);
// 放到数组a对应的部分
for(int i = 0;i<n;i++)
{
a[temp_left1 + i] = result[i];
}
}
void Msort(int* a,int left,int right)
{
if(left >= right) return;
int medium = (left + right) / 2;
// 分
Msort(a,left,medium);
Msort(a,medium+1,right);
// 合
Merge(a,left,medium,medium+1,right);
}
int main()
{
int a[8] = {
1,2,54,64,125,94,64,132};
Msort(a,0,7);
for(int i = 0;i<8;i++)
{
cout<<a[i]<<" ";
}
}
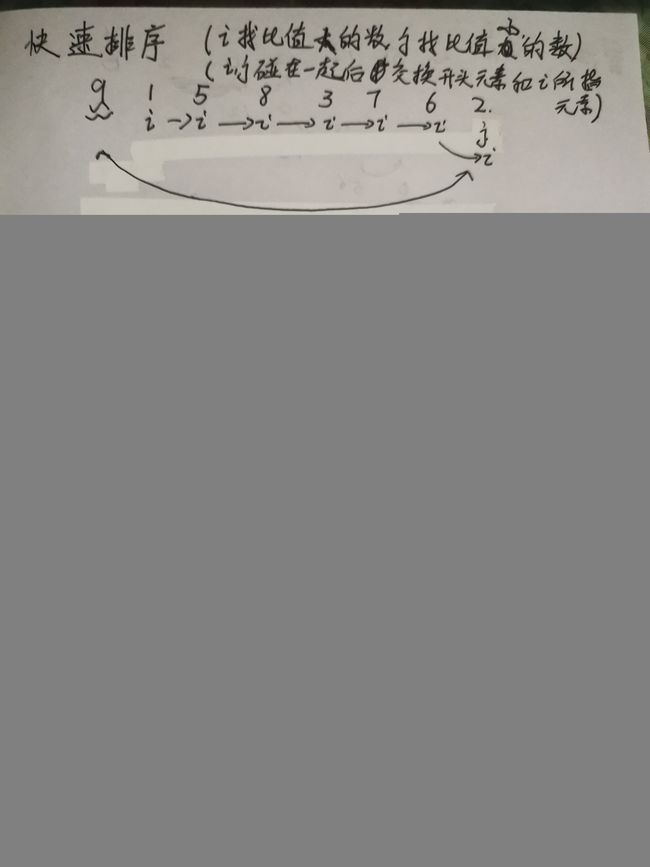
4、快速排序(nlogn)
其思想为选一个数字,将小于该数字的值放在左边,将大于该数字的值放在右边。再将该数字的左右两侧的数组重复该过程。
思路由一篇博文提供,建议阅读以下,比我写的详细很多。链接如下:
https://blog.csdn.net/qq_28584889/article/details/88136498
// 第一个数大小记为temp。将小于temp的放在左边,将大于temp的放在右边
// 返回排序后temp在数组中的位置。
int partition(int* a,int left,int right)
{
int temp = a[left];
int i = left,j = right;
while(i < j)
{
while(a[j] >= temp && i < j)
j--;
while(a[i] <= temp && i < j)
i++;
if(i < j)
{
int nums = a[i];
a[i] = a[j];
a[j] = nums;
}
}
a[left] = a[i];
a[i] = temp;
return i;
}
void quickSort(int* a,int left,int right)
{
if(left >= right) return;
// pos为排序后,第一个数字在数组中的位置
// 如:数组为4 2 1 9 6 5 8 7
// partition后变为1 2 4 9 6 5 8 7
// 则pos为4的位置:2
int pos = partition(a,left,right);
// 对左边排序
quickSort(a,left,pos-1);
// 对右边排序
quickSort(a,pos+1,right);
}
int main()
{
int a[9] = {
2,6,5,9,8,4,1,3,7};
quickSort(a,0,8);
for(int i = 0;i<9;i++)
cout<<a[i]<<" ";
}
桶排序(O(n))
参考的一下博客,读者可自行阅读。
(1)https://blog.csdn.net/bqw18744018044/article/details/81738883?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-3.control
(2)https://www.bilibili.com/video/av17940595?from=search&seid=4032616244052566693
void bucket_sort(double* a)
{
vector<double> bucket[10];
for(int i = 0;i<10;i++)
{
int bi = 10 * a[i];
bucket[bi].push_back(a[i]);
}
int pos = 0;
for(int i = 0;i<10;i++)
{
if(!bucket[i].empty())
{
sort(bucket[i].begin(),bucket[i].end());
for(int j = 0;j<bucket[i].size();j++)
{
a[pos] = bucket[i][j];
pos++;
}
}
}
}
int main()
{
double a[10] = {
0.2,0.5,0.65,0.59,0.62,0.35,0.48,0.98,0.84,0.56};
bucket_sort(a);
for(int i = 0;i<10;i++)
cout<<a[i]<<" ";
}
基数排序(O(d*(n+r)))
参考博客:
https://blog.csdn.net/u012580566/article/details/47702955
基数排序就是分别按个位数、十位数…进行排序。
如:
14 37 56 79 93 78 12 65 30
按个位数排完后为:
30 12 93 14 65 56 37 78 79
按十位数排完后为:
12 14 30 37 56 65 78 79 93
排序完成。
int get_max_bit(int* data,int n)
{
int num = 1;
for(int i = 0;i<n;i++)
{
int bit = 0;
int temp_val = data[i];
while(temp_val != 0)
{
temp_val /= 10;
bit++;
}
if(bit > num)
num = bit;
}
return num;
}
void max_sort(int* data,int n)
{
int tmp[n];
int count[10];
int num = get_max_bit(data,n);
int radio = 1;
for(int i = 1;i<=num;i++)
{
// 每次分配前清空计数器
for(int j = 0; j < 10; j++)
count[j] = 0;
// 统计每个桶中的记录数
for(int j = 0; j < n; j++)
{
int k = (data[j] / radio) % 10;
count[k]++;
}
// count[j]中存储尾数为0~j的数字的个数
for(int j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j];
// 将所有桶中记录依次收集到tmp中
for(int j = n - 1; j >= 0; j--)
{
int k = (data[j] / radio) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
// 将临时数组tmp的内容复制到data中
for(int j = 0; j < n; j++)
data[j] = tmp[j];
radio = radio * 10;
}
}
int main()
{
int data[11] = {
73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 196 };
max_sort(data,11);
for(int i = 0;i<11;i++)
cout<<data[i]<<" ";
return 0;
}
时间复杂度:
设最高位数为d位,基数为r(如基数为10,即10进制,最大有10种可能,即最多需要10个桶来映射数组元素),一共n个数。由代码可见,时间复杂度为:O(d(n+r))。空间复杂度为O(dr+n)。