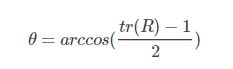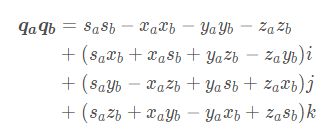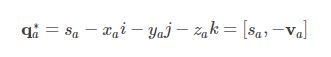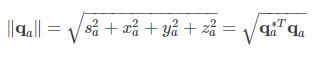三维空间的刚体运动
三维空间的刚体运动
- 1)旋转矩阵
- 2)变换矩阵
- 3)欧拉角
-
- 1、旋转向量
- 2、旋转角:
- 3、转轴:
- 4、欧拉角
- 4)四元数
-
- 1、四元数的定义
- 2、四元数的运算
-
- 1)加法和减法
- 2)乘法(每一项相乘后相加.)
- 3)共轭(跟普通复数一样,虚部取反)
- 4)模长
- 5)逆
- 6)数乘和点乘
- 3、用四元数表示旋转
- 5)练习
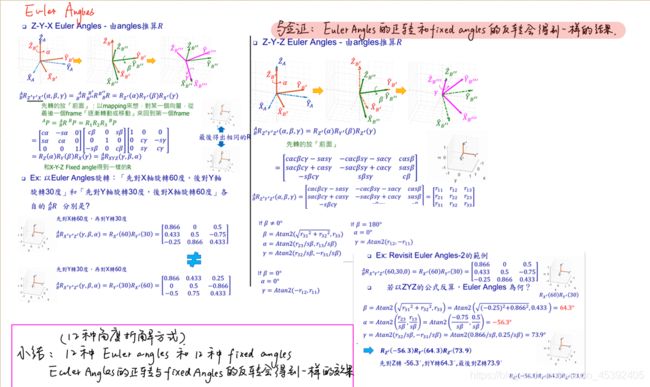
- 6) 台湾大学《机器人学》笔记
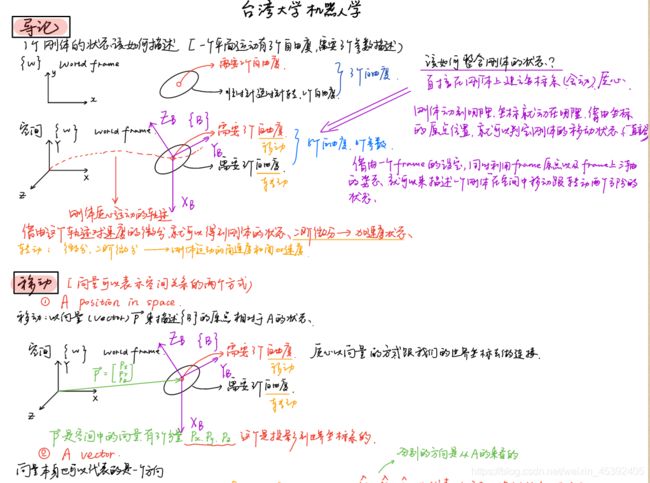
一个刚体在三维空间中的运动如何描述?
我们知道是由旋转加平移组成的,平移很简单,但是旋转有点麻烦。
三维空间的刚体运动的描述方式:旋转矩阵、变换矩阵、四元数、欧拉角。
刚体,不光有位置,而且还有姿态。相机可以看成是三维空间的一个刚体,位置指的就是相机在空间处于哪个地方?而姿态指的是相机的朝向(例如:相机位于(0, 0,0)点处,朝向正东方)但是这样去描述比较繁琐。
1)旋转矩阵
1、坐标系间的欧式变换
欧式变换:相机运动是一个刚体运动,他保证了同一个向量在各个不同的坐标系下的长度和夹角都不会发生变化,这种变化称之为欧式变换。
坐标系1的单位正交基:[e1,e2,e3]
点在坐标系1中的坐标:[a1,a2,a3]
坐标系2的单位正交基:[e1’,e2’,e3’]
点在坐标系2中的坐标:[a1’,a2’,a3’]
则转换关系如下:
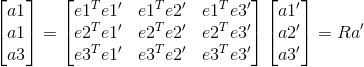
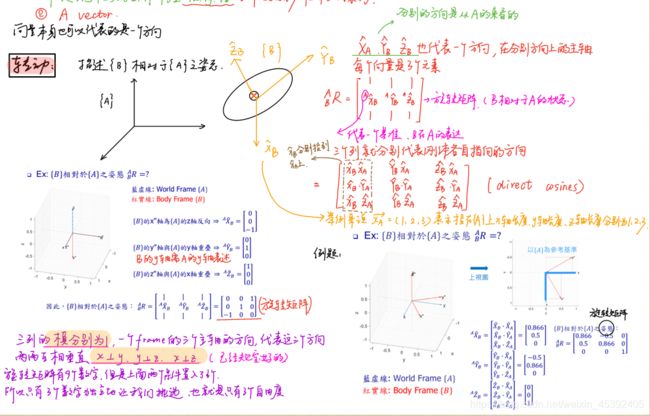
R矩阵,描述了旋转前后同一个向量的坐标变换之间的关系,称之为旋转矩阵(行列式为1的正交矩阵)
旋转矩阵可以描述相机的旋转。
a’=Ra+t,其中t表示平移,这是一个完整的欧式变换。
其中:a为世界坐标系的向量a,经过一次旋转和一次平移t之后,得到了a’。平移只需要把旋转之后的坐标加上这个平移量就行。
2、外积:

外积只对三维向量存在定义,我们还能用外积表示向量的旋转
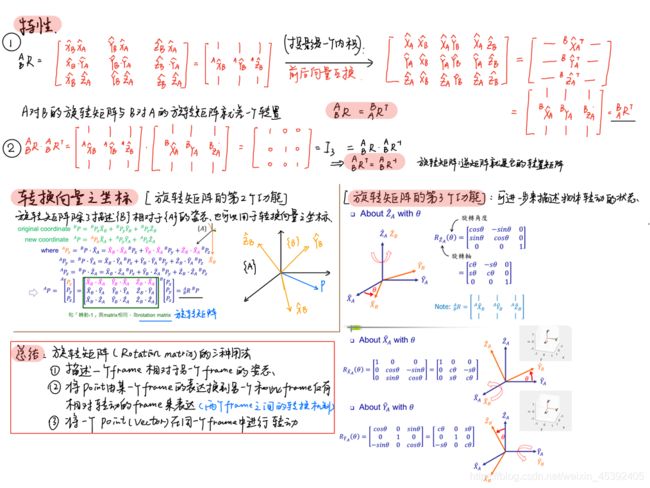
2)变换矩阵
上面的式子完整的表达了欧式空间的旋转和平移,不过存在一个小问题,就是这里的变换还不是一个线性关系,
假设我们经过了两次变换:
![]()
那么从a到c的变换就是:
![]()
但是这样写太过于复杂吧 ,我们引入齐次坐标和变换矩阵
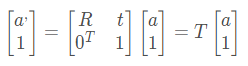
在三维向量的末尾添加1,将它变成一个四维向量,称之为齐次坐标。这个时候将旋转和平移写在了一个矩阵里面,整个关系变成一个线性关系。
T就是变换矩阵
3)欧拉角
1、旋转向量
旋转向量是旋转矩阵的另一种表达方式,使用一个三维向量来描述旋转,由旋转轴n和旋转角θ来刻画。从旋转向量到旋转矩阵的转换过程由罗德里格斯公式表明,具体形式如下:
![]()
2、旋转角:
3、转轴:
4、欧拉角
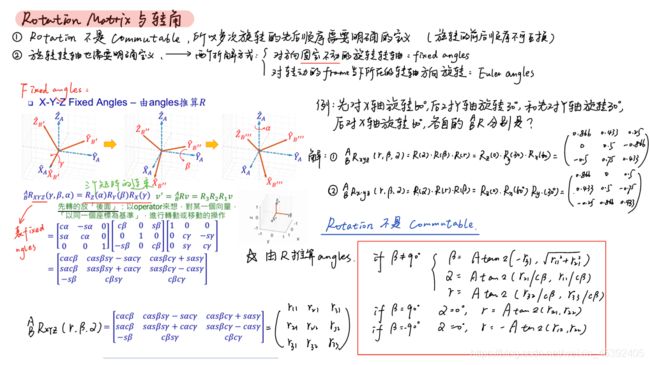
那什么叫做欧拉角呢?
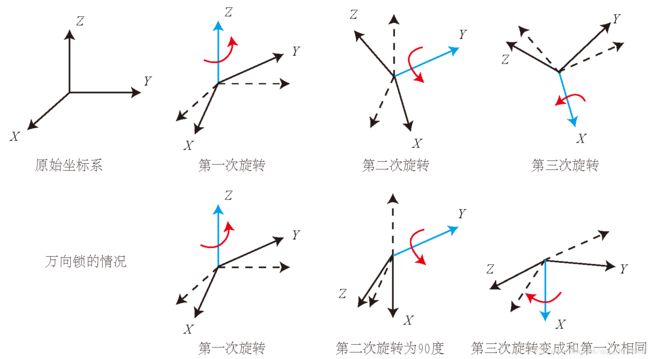
欧拉角提供了一种非常直观的方式来描述旋转,它使用三个分离的转角,即将一个旋转分解成三次饶不同轴的旋转。
ZYX 转角相当于把任意旋转分解成以下三个轴上的转角 :
1、绕物体的 Z 轴旋转,得到偏航角 yaw
2、绕旋转之后的 Y 轴旋转,得到俯仰角 pitch
3、绕旋转之后的 X 轴旋转,得到滚转角 roll
但是欧拉角的一个重大缺陷是会碰到万向锁问题:在俯仰角为±±90度时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失一个自由度。(万向锁问题)
4)四元数
1、四元数的定义
旋转矩阵用9个量描述3个自由度具有冗余性.
欧拉角和旋转向量是紧凑的,但是具有奇异性.
事实上, 找不到不带奇异性的三维向量描述方式
使用复数来表示,有一种类似于复数的代数:
四元数是一种扩展的复数,它既是紧凑的,也没有奇异性.
缺点:不够直观,运算稍复杂.
一个四元数有一个实部和三个虚部:
![]()
三个虚部满足以下关系式:
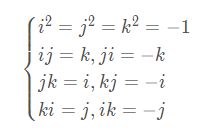
由于他的这种形式的特殊性,人们也常用一个标量和一个向量来表示四元数
![]()
s为四元数实部 ,v 为虚部, 如果虚部为0,表示实四元数;反之,实部为0表示虚四元数.
乘以i表示旋转180°,两个i相乘表示旋转360°
2、四元数的运算
1)加法和减法
2)乘法(每一项相乘后相加.)
3)共轭(跟普通复数一样,虚部取反)
4)模长
5)逆
6)数乘和点乘
3、用四元数表示旋转
5)练习
机器人1号、2号分别位于世界坐标系中。
1号的位姿:q1=[0.25,0.2,0.3,0.1],t1=[0.3,0.1,0.1]
2号的位姿:q2=[-0.5,0…4,-0.1,0.2],t2=[-0.1,0.5,0.3]
注意:这里的q、t表达的是Tcw,且未进行归一化。
设点p在机器人1号的坐标系下的坐标为p=[0.5,0,0.2],求它在机器人2号的坐标系下的坐标。
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
//Geometry模块提供了各种旋转和平移的表示
#include <Eigen/Geometry>
using namespace std;
int main()
{
//一号的姿态
Eigen::Quaterniond q1(0.35, 0.2, 0.3, 0.1);
Eigen::Vector3d t1(0.3, 0.1, 0.1);
Eigen::Isometry3d Tcw_1 = Eigen::Isometry3d::Identity();
Tcw_1.rotate(q1.normalized().matrix()); //q1.matrix()将四元数转为AngleAxis旋转向量
Tcw_1.pretranslate(t1);
//点P
Eigen::Vector3d Pc1(0.5, 0, 0.2);
Eigen::Vector3d Pw = Tcw_1.inverse()*Pc1;
//二号的姿态
Eigen::Quaterniond q2(-0.5, 0.4, -0.1, 0.2);
Eigen::Vector3d t2(-0.1, 0.5, 0.3);
Eigen::Isometry3d Tcw_2 = Eigen::Isometry3d::Identity();
Tcw_2.rotate(q2.normalized().matrix());
Tcw_2.pretranslate(t2);
Eigen::Vector3d Pc2 = Tcw_2*Pw;
cout << "p向量在小萝卜二号的坐标系下的坐标为:" << endl;
cout << "(" << Pc2.x() << "," << Pc2.y() << "," << Pc2.z() << ")" << endl;
return 0;
}