| 1 #-*-coding:utf-8-*-
"""
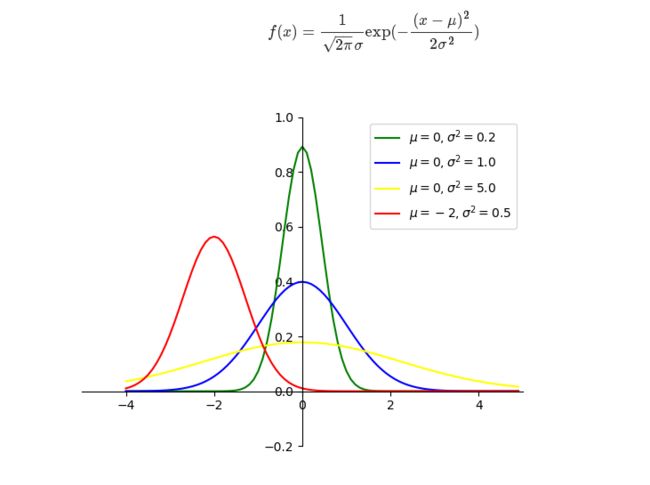
python绘制标准正态分布曲线
"""
# ==============================================================
import numpy as np
import math
import matplotlib.pyplot as plt
def gd(x, mu=0, sigma=1):
"""根据公式,由自变量x计算因变量的值
Argument:
x: array
输入数据(自变量)
mu: float
均值
sigma: float
方差
"""
left = 1 / (np.sqrt(2 * math.pi) * np.sqrt(sigma))
right = np.exp(-(x - mu)**2 / (2 * sigma))
return left * right
if __name__ == '__main__':
# 自变量
x = np.arange(-4, 5, 0.1)
# 因变量(不同均值或方差)
y_1 = gd(x, 0, 0.2)
y_2 = gd(x, 0, 1.0)
y_3 = gd(x, 0, 5.0)
y_4 = gd(x, -2, 0.5)
# 绘图
plt.plot(x, y_1, color='green')
plt.plot(x, y_2, color='blue')
plt.plot(x, y_3, color='yellow')
plt.plot(x, y_4, color='red')
# 设置坐标系
plt.xlim(-5.0, 5.0)
plt.ylim(-0.2, 1) ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data', 0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data', 0)) plt.legend(labels=['$\mu = 0, \sigma^2=0.2$', '$\mu = 0, \sigma^2=1.0$', '$\mu = 0, \sigma^2=5.0$', '$\mu = -2, \sigma^2=0.5$'])
plt.show() |
#-*-coding:utf-8-*-
|