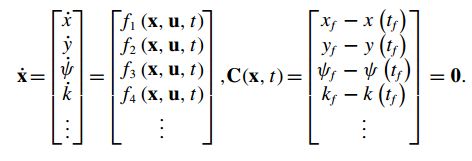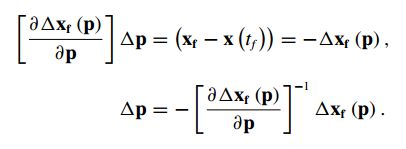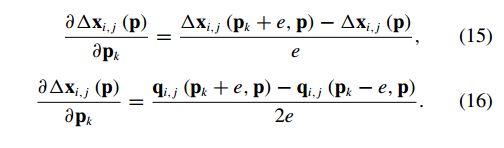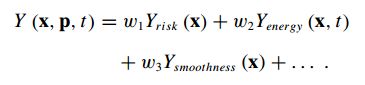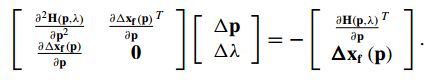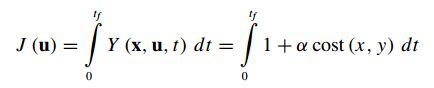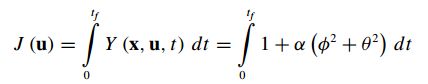Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots 论文阅读笔记

Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots--2007 Thomas M. Howard,Alonzo Kelly

摘要

（1）轮式移动机器人轨迹生成的高程度共性和效率。

共性来源：数值线性化，推进、悬挂、运动前项模型的逆。效率获取：使用快速的数值优化方法和对车辆控制参数的有效初始猜测。

（2）本方法的适用性很广。

可适用于 粗糙的山地、车辆动力学 以及 轮子和山地的交互模型等等其他影响；

可包含边界约束和内部约束 来优化一个目标函数：避障、代价、风险、时间、能量损耗等等；

通过用非线性优化技术来搜索参数化空间的车辆控制，本算法可以达到实时应用。

1、介绍

 · 为了车辆能完全运行在任意环境，移动机器人必须考虑自己的动力学和地形交互的影响。在轨迹生成中 合并这些影响的模型 来决定控制，使达到预定位置。

· 两点边值问题（two-point boundary value problem, 古典和受到广泛研究）：需要求解一个非线性微分方程（位置、偏航角、线/角加速度、曲率约束等），在实际中求解很困难。更因为粗糙的地形耦合这些非线性微分方程，而求解更加困难。

· 数值方法（Numerical methods，本文所展示一种）：由于它典型的采样表示、非线性模型和动态的闭式积分不存在，数值方法需要求解任意地形的这种问题。

1.1 Motivation

真正有用的机器人需要与真实世界交互。轨迹生成形成了自动驾驶能力的基础。实时算法，需要与收集到的感知信息反应。

· 连续的运动，是当代机器人的核心能力。

· 完全的运行，在复杂环境，需要精确理解整个可行运动的空间，并且搜索出一个最优解。简单的方法是线段连接而成的轨迹，在曲率上不连续在动力或运行学上是不可行的。

· 半自动驾驶：轨迹生成器获取一个设定位姿或点，生成轨迹让操作者执行，降低它的工作量。

· 自动驾驶：在获取固定目标点的情况下，轨迹生成可用于获取特定的终端状态；当跟踪某条路径时，轨迹生成器可以通过重新获取某条路径上某个前进位置的运动目标点来校正跟踪误差。

· 轨迹生成也可以作为全局运动规划的核心组成部分。它可以作为一种机制来编码lattice网络空间中状态空间的连通性，lattice网络空间以及满足了所有运动约束。【lattice论文】

1.2 Related Work

在机器人的移动规划中，绝大多数在轨迹生成的研究都是解决——假定平整的地形和简单车辆模型下，找到一条满足nonholonomic约束的无障碍路劲。存在着两种基本方法：sequential search of a graph（序列图搜索）、continuum optimization（连续优化）。

（1）sequential search of a graph

· 路径的边，由动力学可行的低维控制（弧线，回旋曲线等）组成。

· 这个方法生成一个解序列，是一些低维几何基元（geometric primitives）。

· 特点：生成的解是这个离散网络的全局最优解。（a sampled global solution）。

 

  图搜索-轨迹生成相关具体方法：

  1）利用问题的几何性质直接求解未知路径参数的图搜索方法

 · 最优路径的组成：

    ①低维的几何基元：

        序列的线段、曲线（Dubins）、回旋曲线（clothoids）、立方螺旋线（cubic spirals）。【低维的几何基元一些论文】

    ②高维的几何基元：想要在 基元边界（the boundaries of the primitives）之间的连接处 有更高水平的连续性。

        通过定义一序列沿着路径的节点，B-样条曲线 可以符合 任意位置和偏航的边界条件（boundary conditions）。【B-样条几何基元论文】

    ③微分平坦（differential flatness）概念

        这是一类系统的性质，理想地适合于轨迹生成。【微分平坦-论文】

    ④基于正弦和傅里叶序列作为输入函数的方法

         【正弦和傅里叶序列作为输入函数-论文】

 · 缺点：不能生成避障的路径。

 · 【lc见解1】：这里没有提A*和RRT*这两大类相关可以避障的路径发现算法？作者这里的意图应该是不基于网格地图的，类似Hybrid A*那篇论文的one shoot策略，直接生成路径 当前状态--终点状态。    甚至没有提RRT这类基于采样的路径发现算法，个人认为本文作者应该是认为RRT类采样的算法本质上是图搜索，只不过在采样构造图的过程中，完成了搜索。

 

  2）kinodynamic 图搜索方法

  基于网格地图（grid-search）的搜索，可以得到满足 nonholonomic and boundary 约束 的 避障和最短 路径。【Kinodynamic-论文】

· 缺点：在状态空间/控制空间离散的分辨率丢失，只能到达在离散空间中已经存在的边界状态（boundary states）。

· 【lc见解2】：根据之前看的论文，状态空间离散随着状态维度提高，搜素数量指数上升。

 

（2）continuum optimization

· 这个方法生成单一的高阶参数化几何基元。（例如，本文就是控制输入u的参数化）

· 特点：生成连续的局部最优解；在绝大多数场合使用自动控制（automatic control）：这个方法通常使用 数值方法 来满足一些 边界条件（boundary conditions）  and/or 通过搜索 相关参数/采样的控制 来最小化某些代价函数。（automatic control）【论文】

 

变分（优化）技术（ Variational (optimization) techniques）--轨迹生成相关具体方法：

1）① 使用 最优控制 和 3次多项式基元 来生成联合轨迹（joint trajectories）【论文】、

② 把两个边界状态之间的 最小化时间轨迹生成 当成是控制问题【论文】、

③ 应用 shooting method 使用3次样条基元来求解轨迹【论文】、

④ 能量最小轨迹生成方法：通过连续的曲线变形，使其满足边界约束（不适合实时使用）【论文】、

⑤ holonomic几何路径生成，使用最优控制分段光滑方法【论文】、

⑥ 接近实时的最优控制轨迹：解11个满足状态约束的一阶微分方程【论文】、

⑦ 对于微分平坦系统的实时轨迹生成：用线性不等式约束代替了一个合适的非线性约束【论文】、

⑧（当系统是输入输出可线性化）解一个近似线性化的问题对UAV轨迹规划【论文】。

2）最近的一些使用最优控制的轨迹生成方法：

① 使用bang-bang optimal control method对全向轮车辆生成近似最优的路径：满足复杂的动力和执行器模型的最小时间全向轨迹【论文】；

② 本小组提出了一种通过线性化和反求运动方程来解决任意边界状态间的平面轨迹生成问题的实时算法【论文】。

---

之前的移动机器人轨迹生成方法都考虑在平坦的地面上生成。

（3）粗糙地形（rough terrain）的轨迹生成方法：

 1）图搜索方法：使用A*算法基于随海拔高度变化的能量损失的等值线简化地图的搜索空间【论文】。

 2）引入更复杂地形和车辆模型的方法--包含车辆动力和运动学模型【论文】。

3）在地形的B-patch表示上生成最优的B-样条路径【论文】。

4）假定平坦路径为3维地形来生成一条次优的3次样条路径，使用了车辆的动力学和施加地形交互。【论文】。

5）使用一系列曲线基元的图搜索算法：最小化与机器人方向有关的距离和风险。【论文】。

6）另一种两层规划器方法：搜索一个最优的全局路径在平坦地形；局部规划器考虑地形并确保状态之间的连续性：使用best-first search的图搜素问题。

 

1.3 Discriminators

本文算法与前人算法的区别。

（1）当前最优秀的nonholonomic轨迹生成方法，有两类：

   第一类是假定在平整的地形生成光滑的运动基元；  第二类是基于离散控制空间在粗糙的地形上进行图搜索。 

    ——  这些方法在运动基元的连接点处不能产生连续的运动；目前生成连续运动的算法并没有在运动基元的层面上考虑粗糙地形和车辆动态（e.g. 延迟、增益限制、轮子滑动）。

（2）平整地形的假定，解耦了系统的非线性状态方程，极大地简化了这些问题【论文-看一下】；这样做引入了模型误差，后面控制器必须补偿。把地形和车辆动态考虑在内，我们可以在规划阶段预测性地消除一些显著的误差来源，而不是在执行阶段（反馈控制）。

 

1.4 Technical Approach 

本文的技术方法，思路。

（1）轨迹生成问题的一般性描述：在描述系统动态的微分方程f中，生成一系列满足状态约束C的控制集u。（如下图）

（2）本文方法描述——把基本的最优控制问题转化为非线性优化。

  ① 假定一些参数化的控制，控制参数的初始猜测是基于平整地形解的一个查找表。

  ② 从控制到相应的映射，之后根据参数进行数值上线性化，并且在数值上对猜测参数提供一阶更新，解释计算终点到预计终点的偏差。连续迭代改善猜测的控制参数，直到终态误差下降到一定的门限值之下。我们所考虑的搜索空间有很大的收敛半径和很少的局部最优点，使这个方法在实际中有效和可靠。

  ③ 实时、在线生成轨迹。

（3）数值方法的应用，使本文方法可以应用到任意的地形和车辆模型。

上面描述的数值线性化方法，可以应用到任意车辆的前向模型，在粗糙地形上行驶的预测。我们的推进模型包括：执行机构动力学、速率（rate）限制、车轮滑移、速度运动学。

 

1.5 Layout

本文一共有7节。

（1）第2节：描述轨迹生成器的系统结构，包括有过程中 边界状态定义、参数化的控制、数值优化、积分、仿真步的细节。

（2）第3节：讨论车辆控制的初始猜测。

（3）第4、5节：细节展示测试算法能力的实验。

（4）第6、7节：讨论算法的应用、结论和未来工作。

 

2、Trajectory Generator System Architecture

轨迹生成器系统结构。轨迹生成算法分为3级结构：① 轨迹生成（最小化约束误差的数值优化）② 运动预测（对预测模型数值积分）③ 车辆仿真方法。（如下图）

初始和最终状态边界对、参数化的控制和车辆模型构成了轨迹生成器的输入。输出为路径（车辆的状态向量）和正确的控制参数。车辆模型是外部定义，使这个方法不依赖特定的车辆模型。

小节2.1、2.2、2.3、2.4和2.5分别讨论 边界状态定义、参数化车辆控制、轨迹生成（数值优化）、运动预测（数值积分）和车辆的模型。

2.1 State Constraint Definition

一种更简单的轨迹生成问题形式是两点边界值问题（two-point boundary value problem），它便于约束车辆的状态在路径的边界上。需要车辆的初始状态对运动方程进行积分一段前向时间t，并且终止状态定义为车辆的目标状态。

最基本的状态约束包括世界坐标系下的位置  和方向。然而在车辆的悬挂系统和地面的交互之间考虑。状态约束仅考虑或，车辆的控制需要满足初末状态，所以线速度（v）、角速度（w）和加速度（a）通常需要约束在动态可行的运动规划中。机器人初始和目标的一个状态向量的形成：

初始状态用于开始数值积分，终止状态用于约束轨迹的终点。系统约束的形式：

在不同时间强制约束的扩展，或者是状态的任意函数的约束都是很简单的。

2.2 参数化车辆控制

除了边界状态，该算法还需要一组参数化控制来编码车辆的运动。虽然参数化控制空间只能代表所有可行运动的一个子空间，但适当的参数化选择可以代表几乎所有可能的控制。

对车辆的参数化控制集u可以被定义为一个函数，函数包含参数向量p和一些其他的独立变量：

参数向量中的自由参数表示允许算法改变控制形状的旋钮；参数向量中自由参数的数量减去约束的数量表示系统中剩余自由度的数量。

2.2.1 Body-frame Vehicle Parameterized Controls

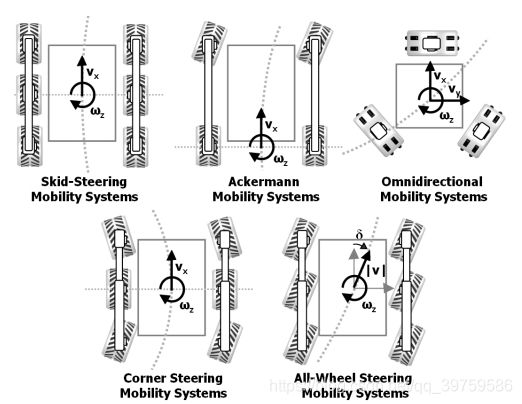
为车辆控制(u)选择合适的设置和参数需要对典型轮式移动机器人的移动系统进行检验。

当它们可以被简单消除自由度来表示时，Nonholonomic约束通常可以便利地表示在体坐标系下。因此，体坐标系下的线速度和角速度是控制的自然候选人，因为它们把输入空间的维度降到最小。这种选择不会失去通用性，因为特定的实现可能会在下面讨论的步骤之前选择包含从车轮水平控制到体坐标系运动的映射。通过悬架运动学映射车架线速度和角速度，得到车轮速度和转向角。

差速、阿克曼和角转向移动系统是最简单的运动模型，因为它们的线速度被限定沿着车辆的x-轴方向。

参数化控制的线速度在x-轴和y-轴通常不是很便利，控制变量的数量超过了系统的自由度【疑问？】，则显式的约束需要重新规定。全向轮转向系统移动平台使用独立的线速度：

差速、阿克曼和角转向移动系统是全向轮转向系统移动平台的特殊例子。

选用了体坐标系下的线速度v和角速度w作为控制候选。

2.2.2 Control Function Parameterizations

对特定车辆移动系统的控制候选已经定义，合适的参数化函数必须选择来表示每个车辆控制的自由度。参数化控制的独立变量  的典型选择为时间（t） 或弧长（s）。

任意的参数化函数可以被应用，只要它对运动方程的解可以进行数值线性化。

线速度外形 

线速度和轨迹的形状是独立的。线速度外形的许多参数是已知的（起点、中间、终点速度通常已知）。

角速度外形

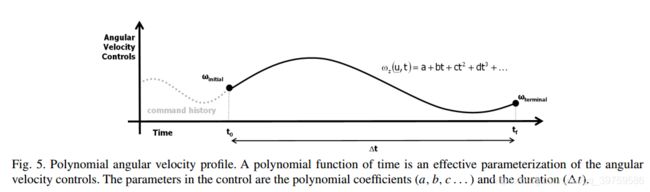
轨迹的形状是由角速度的外形所决定。一个对角速度有效的参数化形式是时间多项式函数。

根据泰勒余项定理，多项式可以代表所有可行的运动，在给定足够的项下达到任意的精确度。它也是可微的，可以提供任何期望的连续性程度。

在解参数化的最优控制问题时，如果所有的自由度在相同的尺度【疑问？】，是最有利于计算的。由于插值方案经常使用多项式函数连接一组控制点，控制点本身是一个等价的表示。

用样条曲线表示角速度外形。

2.3 Trajectory Generation (Numerical Optimization)

        给定边界状态和参数化的控制，用来找正确控制参数的方法是非线性优化。根据问题的约束程度不同，需要应用稍微不同的求解方法。对于一个【全约束问题】（fully constrained problems），定义一个有限的残差并且算法初值合适，算法将会快速收敛到一个可接受的小残差。【欠约束问题】（Underdetermined problems）将会求出很多解，需要从中选取一个“最优”的解。“最优”的指标是定义一些实用函数（utility functional）来判断。

2.3.1 Constrained Trajectory Generation

（1）有约束的轨迹生成形式是最直接的方法。这个修改控制参数变量，直到前向仿真的轨迹终点等于定义的目标终点状态，同时满足约束C(x)。一些边界约束可以简单求解，因为可以直接等于确定的控制参数（如，初始速度）；困难的约束（如，位置）必须用数值方法来进行数值求解。

        数值方法的方法用的是牛顿法。对运动方程解的雅可比矩阵进行求逆（inverted），以找到一个对系统中所需参数的修正，使约束误差最小化，约束误差我们目前将其定义为仿真终端状态与终端边界约束的差值：

        如果约束的雅可比矩阵是非方形的(当约束向量和参数向量的长度不相等时)，可以使用伪逆【伪逆的效果？】来生成最小二乘或最小范数解，从而生成参数修正向量。

（2） 由于运动方程的积分的偏导数一般不能被解析求解，必须进行数值上的估计【论文】。前向(eq.(15))或中心差(eq.(16))运动方程的线性化可以用来估计这些偏导数。该算法通过对所有偏导数的数值估计，推导出车辆独立性。

2.3.2. Constrained Optimization Trajectory Generation
 

        除了应用伪逆，最优控制方法可以被使用来求解非完全（underconstrained）约束的问题形式。在这种情况下，优化过程会创建额外的必要约束来定义局部唯一解。

        在最优化问题的形式中，线速度和角速度的控制参数(p)必须被调整来满足这些约束和最小化一些实用函数（utility functional）J（p）。这是用拉格朗日乘数法实现的，哈密顿量(H)定义为代价函数和拉格朗日乘子向量与约束的乘积：【论文】

        实用函数描述了我们想要如何优化的路径。一般来说，它采用这种形式：

实用函数（utility functional）被设想为沿着未知路径的潜在时变实用函数(Y(x, p, t))的线积分。同样地，这个问题可以用代价（cost）而不是效用（utility）来表述。时变实用函数（utility functional）可以被认为是状态向量上的一个(潜在的时变)场。它代表了作为一个给定状态属性的效用或成本的任何加权组合。它可能包括瞬时能量消耗、车轮打滑、丧失机动性、风险、坡度、道路平滑度、接近障碍物或其他任何感兴趣的东西。

最优性的一阶必要条件是众所周知的：

        该系统共有n+m个方程，其中n为参数向量的长度(以及系统中未知参数的数量)，m为拉格朗日乘子向量(及系统中约束的个数)。

        该系统通过线性化一阶必要条件来求解。在每一次迭代中调整自由控制参数的初始估计和拉格朗日乘子，直到找到局部最优解。在这一点上，Hessian梯度和边界状态的误差都趋于零。优化的每次迭代都涉及到的数值解：【求不了二次导数怎么办？】

通过求逆得到控制参数和拉格朗日乘子向量的修正因子：【求不了逆怎么办？】

当初始估计与局部解距离较远时，采用步长比例因子来增强数值稳定性。代替比例因子，最佳步长可以通过执行更耗时的线搜索来确定。

哈密顿量(H)的Hessian矩阵，就像前向解的雅可比矩阵一样，不能在我们的情况下解析求解。同样，正向差或中心差被用来估计偏导数：

· 【lc理解3】：根据输入的控制参数p，前向积分运动模型得到仿真的，仿真得到的与实际的终点状态相减为偏差。牛顿法：由偏差对控制参数求偏导 -- （前向积分运动模型的偏导要数值求解）,来更新控制参数p，得到使偏差减小为0的最优控制参数p。【还有一些问题？：时间设置问题、角速度大小约束问题、哈密顿函数的Hessian矩阵数值求解、比例因子增强数值稳定性、最佳步长使用线搜索（更耗时）代替比例因子  的实际实施？】。

2.4. Motion Prediction (Numerical Integration)
 

        对控制车辆运动的微分方程进行数值积分的过程本质上是一个仿真过程。运动仿真需要生成对应于参数化控制的轨迹，并且哈密顿函数的雅克比和海塞矩阵也是因此求解（通过前向解的数值线性化）。  这个过程分为3个不同的步骤：控制动态（control dynamics）、轮子与地形的交互模型（modeling of the wheelterrain interaction）和运动仿真（motion simulation）。

（1）第一步，模拟控制动态，是十分重要的对真实世界系统的精确仿真。实际的系统有电机加速度和转矩限制、延迟和joint limits，这些都必须被模拟来生成一个实际的车辆响应控制命令的仿真。运动预测阶段的控制动力学建模部分简单地决定了车辆对体坐标系下线速度和角速度控制的响应:

（2）第二步，模型的控制动力学部分决定了车辆将施加在环境上的力，因此产生了环境的响应力。在这里，车轮滑动、滑动和外力作用于系统的模型被应用。

（3）第三步，运动预测的最后一部分是实际的运动仿真，决定了一小时间步下车辆位姿的改变。

由于地面车辆通常不能控制其滚转、俯仰或仰角率(它们是环境和悬架之间相互作用的函数)，这些状态的新估计由悬架模型在每个运动预测步骤的最后进行计算。

2.5. Vehicle Model (Vehicle Simulation)
 

        从问题的角度来看,汽车模型部分的轨迹生成算法是一个抽象的车辆模型类的实例，确定机器人将如何响应命令线速度和角速度控制，改变它的位置和姿态，并与环境交互。汽车模型通常分为四个元素：一个动态模型，一个轮子/地形交互模型，运动模型和悬架模型。

2.5.1. Vehicle Dynamics Models

车辆动力学模型模拟车身框架车辆命令对车轮扭矩和/或速度的响应。通过对参数化控制的响应建模，得到的解是动态可行的。

（1）车辆动力学模型的一些元素是速率限制，关节限制，和延迟。速率限制代表执行机构转弯速度的限制。建模这些影响可以解释驱动轮移动慢于要求或转向伺服落后于他们所期望的方向。

这些类型的约束，可以通过对动力学运动模型输入控制进行积分的响应 在轨迹生成器中施加，而不是直接控制。硬限制可以施加在转向角度、模型的执行器动力学可以模拟在电机控制器的延迟。

（2）体坐标系下的控制命令--到--轮子的执行

2.5.2. Wheel/Terrain Interaction Models
 

通过在整个自主系统的规划阶段预测车轮/地形的相互作用，而不是在执行阶段考虑，可以生成更动态可行的车辆运动。【论文】

2.5.3. Vehicle Motion Models
 

车辆移动模型将车辆体坐标系下的线速度和角速度映射到世界坐标系的位置和方向率。

车辆的运动学模型。——比如差速小车的运动学模型。

2.5.4. Vehicle Suspension Models

车辆悬架建模是在给定车辆当前状态的其他因素的情况下，正确确定车辆的姿态和高度的问题。这是一个嵌入式优化问题，它通常是高度欠确定的。我们解决这个问题的概念是允许车辆漂浮在高度和姿态，并明确在悬架，同时尽量减少车轮和地面高度下(或以上)他们之间的残差。

 

3、车辆控制参数的初始猜测

对车辆控制参数的好初始猜测，对于轨迹生成算法的效率十分重要——迭代次数和局部最优。由于三维地形、任意车辆动力学和任意地形模型的初始猜测很难计算(因为它们的维数)，因此考虑了有限动力学条件下的平坦地形解作为初始猜测值。在历史上，解决方案的近似值是从几个维度的数据上通过手工调整多项式函数来找到的【论文】。本节讨论为初始猜测生成数据集的问题，以及存储它们的两种方法:初始猜测查找表和神经网络。

3.1 查找表

查找表是一种有效的方法来存储车辆控制参数的初始猜测，在给定的解决方案空间是低维的，是平滑的情况下。这也是使用参数化控制的另一个原因，因为它们在相对较少的内存中编码轨迹的整个形状。

通常影响路径形状的最重要的边界约束是初始和终点位置(x, y)，偏航角()，初始和最终曲率(k0, kf)，得到解参数向量的五维查找表。如果速度等更多维度对初始猜测的准确性有显著影响，则可以将它们合并到查找表中。

为了有效地生成初始猜测查找表，我们使用在表中先前的解启动邻近轨迹生成问题。这需要对第一个轨迹生成问题有一个令人满意的初始猜测，理想情况下，它位于查找表的中心位置。

在实践中，如果观察到收敛问题(由于离散化的动态不可行性或稀疏性)，可能需要调整通过初始猜测查找表的每个维数的级数的顺序。存储的查找表的分辨率和维数与机器人的存储和计算能力有关，因此与平台有关。

3.2 神经网络

另一种生成轨迹生成器中使用的初始猜测的方法是使用机器学习算法来拟合一个函数到大量轨迹生成示例的训练集。3.1节中的初始猜测查找表(或它的采样版本)可以作为一个良好的训练集，因为边界状态对是有规则地分离的。

使用这样的表示法背后的动机是节省空间。一个高维的初始猜测查找表可能需要几十或几百兆字节的存储空间，而一个神经网络，仅仅需要保存学习函数的一些参数，仅需要几千字节的空间。这对于存储空间有限的应用程序很重要，比如行星漫游者。这些解决方案是机器学习算法的很好的候选方案，因为这些解决方案的参数通常是平滑和连续的。在这种情况下应用神经网络的缺点是学习整个函数的前期成本。

4. 实验装置

使用上述方法和算法，我们已经建立了一个任意车辆的连续原始轨迹生成器，并且在运动预测中考虑到地形几何。实验和模拟将使用基于“岩石8号”原型火星漫游者的运载模型(图8)。该车有一个全轮转向机动性系统，在随后的一些例子中人为地受到限制，以演示较差机动性系统的轨迹生成。本节将概述状态约束(4.1节)和控制参数化(4.2节)，轨迹生成算法实现(第4.3节)，悬架模型(第4.4节)，车辆动力学模型(第4.5节)，以及实验中使用的模拟环境。

 

4.1 状态约束

对于第5节中的一系列例子，我们将解决通常与轨迹生成相关的两点边值问题。但需要注意的是，通常算法不需要在边界处指定状态约束。可以在任意数量的时间点上指定任意数量的约束。

轨迹发生器优化只需要满足终端位置、目标、方向和曲率。位置、航向、方向和曲率初始状态约束使用车辆的当前状态被简单地解决。

4.2 控制参数化

这个实现采用五阶多项式样条函数在曲率和线性轮廓线速度和方向。曲率函数的使用方式与角速度是相同的，两者是可互换的。在初始控制上有人为的约束——它们等于初始曲率、线速度和最大连续性的方向状态约束。

4.3 轨迹生成算法实施

由于参数向量(8)的长度超过了约束向量(6)，系统可以使用有约束或约束最优轨迹生成技术进行求解。在第5.1-5.5节中使用了约束轨迹生成技术(第2.3.1节)，在第5.6节中使用约束最优技术(第2.3.2节)。

4.4 Suspension /Kinematic Model

为了将车体速度映射到车轮速度，并在任意地形下确定车辆的方向和构型，必须对车辆悬架进行建模。以类似Tarokh和McDermott(2005)【论文】的方式计算了车身到车轮的运动学方程。车辆可以建模为一系列的转动关节和连杆，如图8所示。

悬架模型作为一种数值优化(牛顿方法的另一种应用)被实施，通过调整摇杆-转向架的三个自由度以及横摇、俯仰和仰角来最小化车轮接触点和地形之间的距离。一般来说，优化所要求的偏导数必须通过数值求解。然而，通过对车轮接触点正运动学方程的偏导数对车身框架的仰角、姿态和悬架自由度进行解析，可以得到雅可比矩阵的估计。该解在与地形接触的前轮上进行了在线有效计算，在利用前一状态进行前轮动力学解时进行了有效计算(悬架，姿态，高度)作为悬架最优的初步估计。

4.5 车辆动态模型

变化的动态模型，包括车轮滑移模型和滑动模型将在第5.5节中演示。章节5.1-5.4和5.6中的例子应用了理想的车辆动力学模型，以便隔离建模的不同方面的影响。一般来说，所有这些应用都可以使用任意复杂的车辆模型(关节极限、电机模型等)，但需要较高的计算成本。

4.6 仿真环境

实验中的地形以分形生成的海拔图表示。采用三阶拉格朗日插值方法【？】确定环境中任意位置的高度。由于三阶拉格朗日插值在图单元之间的边界上提供连续的导数，这种方法比简单和成本更低的线性插值方案更受青睐。

5、实验和结果

本节演示了一些已开发的轨迹发生器的使用。通过比较使用粗糙地形和传统轨迹生成的路径，首先展示了在正演模型中包含地形几何的必要性。    然后，讨论了该算法的收敛速度和收敛行为，并举例说明了不同机动系统的运动生成，在车辆动力学是重要的情况下，以及最优轨迹的生成。

该算法的主要目的是通过对模型进行反求，生成符合模型中所编码的动态约束和问题规范中所编码的边界约束的可行运动。所使用的模型的逼真度是一个重要而独立的问题，只能在真实车辆上进行评估。我们断言，然而车辆模型的参数可能会改变，以便在实际中更好地校准；我们的轨迹发生器仍然可以求它的逆。该算法已在喷气推进实验室的CLARAty系统中集成，并在Rocky 8原型移动机器人平台上成功进行了现场测试。它还被用于定制设计的无人地面车辆(军用机器人原型)和在机器人竞赛中使用的自动化汽车。

由于篇幅所限，本文只给出了相对较少的具体例子。

5.1 粗糙地面的轨迹生成

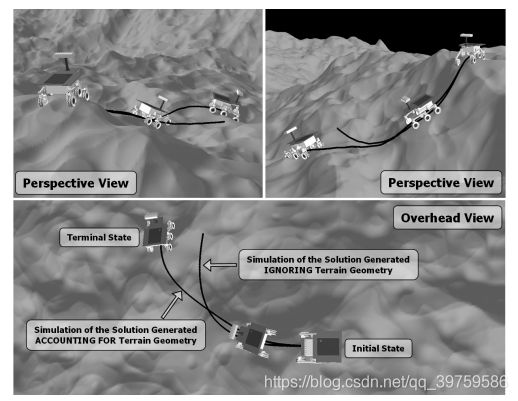
在粗糙地形环境下，轨迹生成中考虑地形几何是非常重要的。图9显示了交替假设和不假设平坦地形所产生的轨迹的两个正演模拟。粗糙地形解满足严格的终端约束(在三次迭代中)，而在这个例子中平坦地形解相对位置差24.1%，相对航向差11.5%。

从这个图中可以看出三个重要的方面:

（1）在运动模型中忽略地形几何的影响会导致不正确的轨迹。

（2）假设平坦地形生成的任何路径都会比一般表面上任意两种状态之间的真实三维路径短。忽略地形几何形状产生的轨迹会使转弯过早，因为车辆不会意识到它只是取代了其表面(x, y)位置变化的一小部分。

（3）平坦地形的解与真实地形的解非常接近，可以为粗糙地形轨迹生成算法的初始化提供初始猜测。即使在像图10所示的大的地形起伏中，收敛通常需要少于三次迭代。

当然，在现代机器人系统中，这类误差通常使用反馈控制和路径跟踪来处理。然而，这里的重点是，使用本文的方法可以完全避免这些错误，因为在局部规划中使用的感知可以告知算法关于地形的几何。

5.2 轨迹收敛

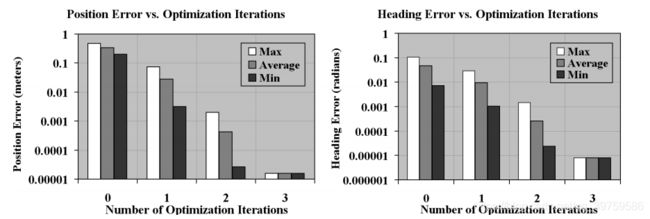
为了证明对车辆控制参数差的初始估计的鲁棒性，与第5.1节相同的问题通过人为地对控制参数差的初始估计和更小的步长尺度因子（a = 0.625)。图10和11显示了轨迹，表示轨迹生成器需要收敛到达到目标终端状态的解决方案的九个迭代步骤中的每一个步骤。

图11显示了牛顿法的收敛性，因为参数校正与当前状态误差成正比。即使在初始猜测误差较大的情况下，由于解空间的相对凸性，该算法仍能收敛到正确的解。

5.3 对车辆位姿有严格移动约束的粗糙地面轨迹生成

移动机器人的设备放置问题（Instrument placement problems）通常需要一个局部规划算法来生成一个终端状态的轨迹，该终端状态的位置和航向是确定的。位置和航向边界约束通常设置为使目标处于科学仪器的运动范围或传感器或摄像机的视场范围内。

为了演示所介绍的轨迹生成算法的一个更一般的例子，我们使用该算法来规划访问七个顺序的科学目标的轨迹，如图12所示。这里，模拟移动机器人的全轮转向能力受到限制，以演示滑行转向、Ackermann和转角转向移动系统的运动规划(线速度被限制为沿着车辆的x轴)。

在这种情况下，在考虑地形几何形状的情况下，算法在少于4次迭代的情况下满足了所有12条轨迹的终止条件。与前面的例子一样，这说明了算法在相对困难的地形几何中快速收敛，同时说明了所述方法的典型应用。

5.4 在全向轮移动系统下，对车辆位姿约束的粗糙地面轨迹生成

在任意地形下为全轮转向移动系统生成路径的能力可以赋予机器人在环境中高效移动的能力。这对于能量有限、环境可能充斥着障碍物以及机器人的定位(部署科学仪器)的行星机器人应用来说尤为重要。与5.3小节相同的仪器放置问题呈现在图14，唯一不同的是机器人可以使用全向轮移动系统。运动计划说明了该算法可以利用全轮转向产生更平滑，更有效的运动计划，为多个排序的仪表安置问题。图15绘制了位置和航向误差作为算法迭代次数的函数。

在这种情况下，在考虑地形几何和全轮转向能力的情况下，7个轨迹在少于6次迭代中满足终止条件。约束误差较大，因为最初的猜测没有考虑到全轮转向能力的车辆。在实践中，这些解决方案可以编码到车辆控制参数的初始猜测中。

在比较第5.3节和第5.4节中提出的器械放置场景的运动方案时，四轮转向运动方案显然更短，更有效。

5.5 考虑车辆动力学的轨迹生成

数值线性化的一个优点是可以纳入任意的车辆动力学模型。动态影响往往在局部运动规划层面被忽略，而在较低的层面上通过反馈控制加以处理。我们的算法允许动态模型的车轮-地形相互作用和其他车辆动力学在轨迹生成解决方案之前处理。

5.5.1 考虑车轮滑移模型的轨迹生成

车轮滑移补偿是目前行星移动机器人最重要的移动问题之一【论文】。算法的收敛性不能保证任何车轮滑移模型，因为求解需要合理的初始猜测。然而，如果一个合理的初始猜测被提供并且仍然没有达到收敛，那么可能没有动态可行运动。

由于轨迹发生器使用车体坐标下速度控制的响应，因此需要先确定单个车轮速度，在每个车轮上应用滑移模型，然后反演车体动力学来估计车体速度响应。虽然这种方法不像基于力的车轮滑移模型那样有原则，但是这种近似在实际中经常使用，所以我们将在这里使用它。

一个涉及轮子滑动的典型问题是为行星探测车在爬坡时规划轨迹，如图16所示。对这些应用的典型车辆滑动模型，姿态的响应与控制速度耦合。当车轮滑移不在轨迹生成器中建模时，路径会出现过短。然而，我们可以使用所提出的轨迹生成算法来计算符合这些车轮滑移模型的目标状态约束的路径。

在轨迹生成中补偿车轮滑移。车轮滑移模型可以包括在车辆模型中使用轨迹发生器规划运动。需要注意的是，正演仿真所生成的无滑移运动模型的滑动运动明显小于预测，且未达到目标终端状态。改进的路径跟踪算法的性能可以期望通过建模这些影响，而不是依赖反馈控制来负责这些误差。

这里使用的车轮滑移模型根据车辆姿态计算每个车轮的车轮滑移百分比。模型参数与现场试验结果一致。一般情况下，任何车轮滑移模型都可以在车辆模型中实现。

图17显示了图16所示的两条路径的命令和响应线速度和角速度。注意，由于车轮滑移模型的净速度响应总是低于命令速度，因此合并车轮滑移模型产生的路径执行时间更长(9.21 s vs. 6.16 s)。另外，请注意，尽管命令很流畅，但响应速度并不是特别流畅的函数。

5.5.2 考虑车辆动力学模型的轨迹生成

车轮滑移不是唯一可以包含的动力学的形式。我们将用“滑动”一词来指车轮的意外侧向运动。滑动或滑动动力学可以纳入控制动力学模型，以产生轨迹，以自动补偿这些运动。例如，图18中的行星机器人试图沿着给定的轨迹穿越一个斜坡。如果在没有对斜坡的滑动效果建模的情况下生成并遵循该计划，机器人将滑下这个山丘。这种效果可以很容易地建模为与地形坡度成比例的速度，从而形成一个计划的轨迹，驱动上山来补偿向下滑动的效果。

在本例中，轨迹发生器在算法的五次迭代中都能够满足边界状态约束。图19显示了建模和未建模的车辆动力学解决方案的命令速度和响应速度。请注意，未建模的解决方案没有考虑到从山上滑下来的原因，因此角速度一直保持为零(终端状态在初始状态的正前方)。包含这些影响的解决方案明白，为了补偿这些影响，它必须在最初的坡面，因此它有一个非零的角速度外形。

5.6 在粗糙地形使用约束优化方法生成轨迹

只要有足够的自由度来优化某个东西，最优控制形式就适用。我们介绍两种不同例子的轨迹优化形式，定义使用最小代价和最小斜坡驻留效用函数。重要的是要注意到这些轨迹只在由多项式控制集张成的可行运动空间上是最优的。然而，我们也认为这个空间是任意控制的连续函数空间的一个很好的近似。

5.6.1 最小代价性能指标

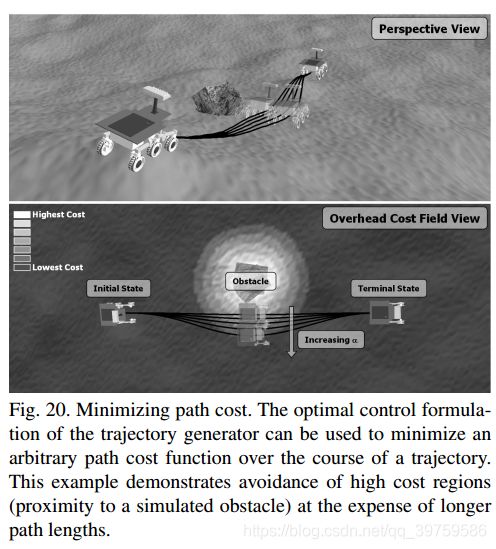
在这种类型的公式中，障碍物表示为机器人需要穿越的代价。如果一个高成本的障碍被观察到在计划的轨道上，典型的车辆必须要么在全局层面上重新计划，要么从目标路径中暂时转向并且在绕过障碍物后重新获取路径。在轨迹发生器的最优控制公式中动态生成转向运动，在总代价函数中考虑最小代价和最小时间的权衡。

要找到最好的折衷办法，效用函数(Y(x, p, t))定义为1和成本地图在当前位置(x, y)的加权值之和。

积分中的“1”项表示穿越一个单元格所需的时间，而“cost(x, y)”则表示穿越该单元格所需的代价。参数控制在寻找最短路径和使成本线积分最小的路径之间的权衡。当趋于零时，将找到最小时间路径。相反地，当a趋于无穷大时，会找到局部最小代价路径。

一个简单的例子可以证明这个效用函数的有效性，它避免了模拟的局部化障碍。一个代价场（cost map）可以通过对障碍物的接近度进行惩罚来产生，如图20所示。

5.6.2 Minimum-slope-dwell性能指标

对于在崎岖地形上运行的行星漫游车来说，有时有必要尽量减少在斜坡上花费的时间，以减少风险。因此，我们可以定义一个效用函数来惩罚沿路径的高滚和俯仰值，以避免倾斜：

与5.6.1节中的最小成本示例一样，“最小”术语表示在最小时间和最小斜坡驻留解决方案之间的权衡。由于我们使用的数值技术是下降算法，我们将只找到局部最优值，所以当许多这样的极小值普遍存在时，不经过修改就不能使用该技术。

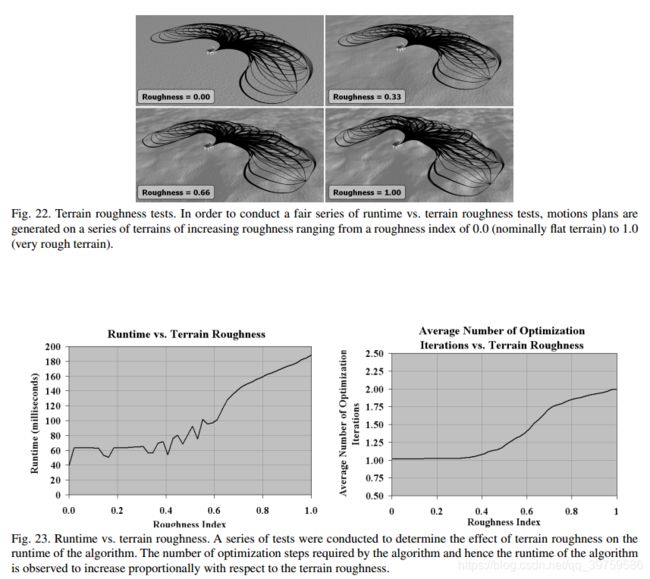
5.7 运行时间性能

在轨迹生成中使用的车辆模型的复杂性和地形形状对算法的预期运行时间有显著影响。本节以实际车辆模型为例，对所提出的粗糙地形轨迹生成算法进行了性能测试。

运行时可能非常依赖于地形的粗糙度，因为使用的悬挂模型的复杂性。

6 应用

我们的算法可以赋予移动机器人一种前所未有的能力，在相对具有挑战性的环境中预测其自身行为的后果。使用它，我们可以在应用程序中期望智能行为，如本节中概述的局部规划和避障、路径跟踪和全局规划。

6.1 局部运动规划

该轨迹生成方法最明显的应用是复杂环境下的局部运动规划。

局部运动规划的一种方法是自我-建图，它是通常用于避障的以身体为中心的搜索空间【论文】。该算法能有效地生成自图(图24)，并能编码车辆动力学约束。

为了更好地评估可行性和真实路径成本，自我图最初可以在一个平坦的地形假设下生成，然后适应任意的粗糙地形和动力学模型(图25)。由于该算法生成的自图只是边界状态对之间求解的路径集合，因此该算法能够以平坦地形解作为初始估计，有效地适应粗糙地形。

6.2. Path Following
 

路径跟踪是寻找车辆控制的问题，使移动机器人跟踪其目标路径。典型的路径跟踪算法依赖于一个相对快速的反馈控制回路，使用一个低阶运动基元，在某个前向点重新获得目标路径(例如，纯追踪)。由于更新速度快，可以补偿未建模误差，因此该方法已成功实现多年。

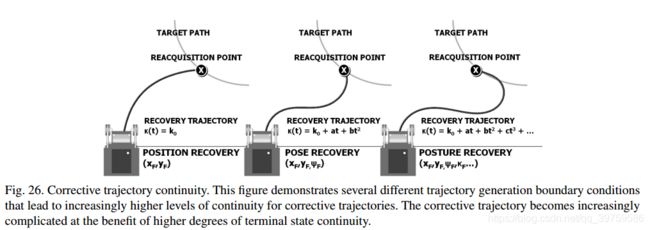
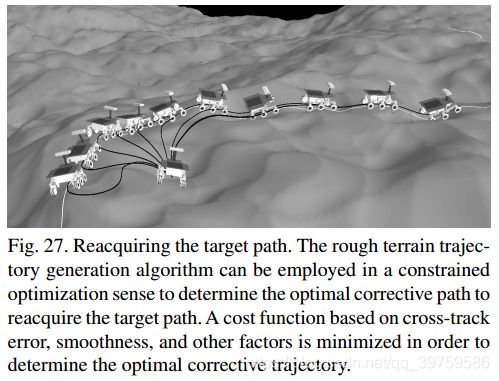
如Howard等人(2006)所述，一种更鲁棒的路径跟踪算法可以基于真实的动力学模型和车轮-地形交互作用生成车辆控制【论文-鲁棒的路径追踪算法】。通过粗糙地形最优轨迹生成算法生成一组候选路径跟随运动，该算法在保证位置、航向和曲率连续性的前提下重新获取某前方车辆姿态下的路径(图26)。修正轨迹的最优选择被选择，使基于交叉轨迹误差、平滑度和任何其他任意因素的效用函数最小化(图27)。

6.3. 全局运动规划
 

轨迹生成可用于为全局运动规划创建内在可行的搜索空间。如图28所示的一种技术是创建规则的lattice-state并将它们与可行运动联系起来这些可行运动作为状态间转换的边。最初，由于平移和旋转下节点关系是对称的，且其大小与单元格大小一致，因此可以根据一个平坦的地形查找表生成边缘，并且几乎不需要明显的形状。

此后，在搜索中实际遍历这些边缘时，可以根据地形形状对边缘进行单独调整，以加强连续性;在计划执行过程中，感知信息细化地形形状时，可能会再次对边缘进行调整。

7、 结论

这篇文章提出了一种高度通用的方法，为移动机器人的轨迹生成多少任意的移动特性。这样的一般公式被提出是因为它允许在计划时间预测消除模型误差，而不是在执行时间反应消除。鉴于地形跟踪、车辆动力学和车轮/地形交互的模型具有任何效用，我们的方法可以提取和利用这些模型中的信号，同时在控制执行过程中留下剩余的不可预测的组件进行补偿。

该算法可以赋予移动机器人前所未有的能力，以预测其自身行为的后果，并在相对具有挑战性的环境中采取纠正行动。利用它，我们可以期待如下的智能行为:

由于执行器动态模型模拟了转向系统的迟缓性，一辆自动客车能够以精确的正确量提前开始转向，以便在交通中变道。

一种行星探测车，可以利用它的车轮滑动的预测，通过接近一个山坡上的目标，预期滑进目标的轨道执行。

一辆无人驾驶地面车辆执行扫荡埋藏的地雷可以改变其轨道响应实时高分辨率地形信息。这样的改变将确保目前的传感器带与最后的精确平行，无论部署的飞机所生成的空中地形图可能有多差。

在实际应用中的性能当然取决于模型的逼真度。模型逼真度的问题不在本工作的范围之内。然而，即使是不完美的名义模型，也比完全缺乏一个模型更好，这说明了当代艺术的状态，就这里介绍的元素。

 

 

当前和未来的工作包括在多种环境中使用该算法。首先，将其应用于粗糙地形路径跟踪中校正机动的生成。其次，它被用于生成良好分离的轨迹集，用于粗糙地形车辆的避障计算。此外，作为一种更大规模的非完整运动规划器的搜索空间生成组件，它正在被评估和改进。

 

---

参考文献：Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots.  Thomas M. Howard; Alonzo Kelly