leetcode日记(2021/02/20)

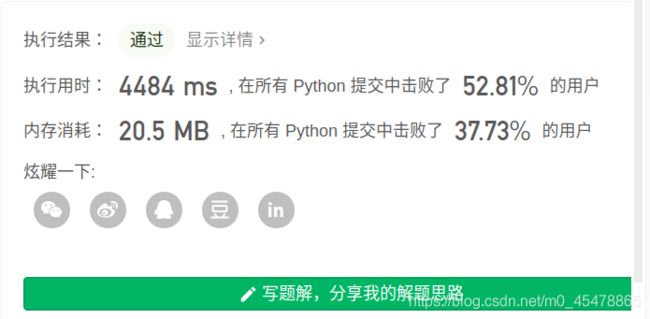
最长回文子串

如果一个字符串是回文的，那么去掉头尾两个字符之后也一定是回文的，所以我们判断一个字符串是否是回文的问题可以转化为动态规划问题，转移方程: dp[i][j]=(s[i]==s[j] and dp[i+1][j-1])

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        一个字符串如果是回文串，那么他的子串也一定是回文的
        从单个字符串展开，如果一个字符串两端相同字符，并且中间是回文的，那么这个字符串
        是回文的
        因此只需要知道两个字符串之间的子串是否是回文的，就可以知道这两个子串是不是回文的
        需要注意的是，循环的流程是i从倒数第二个开始，j从i的后一位逐步遍历，这样才能保证
        在访问当前字符串时，子串已经访问过了
        """
        str_len=len(s)
        dp=[]
        for i in range(str_len):
            dp.append([False]*str_len)
            dp[i][i]=True
        
        left=0
        right=0
        for i in range(str_len-2,-1,-1):
            #一定要让i从后向前，然后j从i+1到末尾，这样才能保证i和j之间的子串已经是访问过的
            for j in range(i+1,str_len):
                if (dp[i+1][j-1]==True or j-i==1) and s[i]==s[j]:
                    dp[i][j]=True
                    if dp[i][j]==True and j-i>right-left:
                        left=i
                        right=j
        return s[left:right+1]

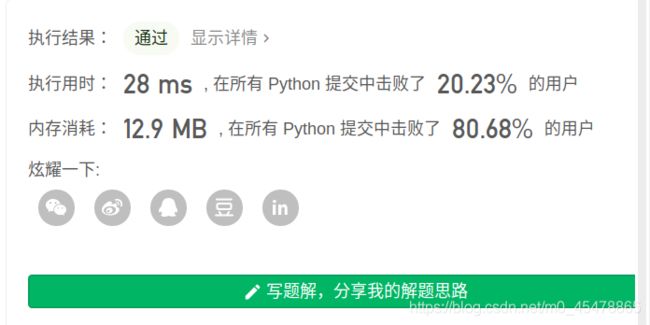
不同路径

显然，到达一个格子可能的路径数目是这个格子的左边加上上边两条路径的数目之和，这是一个DP问题。
初始化dp二维数组，其中第一行和第一列是1，其余位置是0
转移方程：
dp[i][j]=dp[i-1][j]+dp[i][j-1]

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        dp=[[1]*n]
        for i in range(m-1):
            dp.append([1]+[0]*(n-1))

        for i in range(1,m):
            for j in range(1,n):
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]

不同路径 II

思路是一样的，如果遇到障碍物，那么这个格子的位置数值填0

class Solution(object):
    def uniquePathsWithObstacles(self, obstacleGrid):
        """
        :type obstacleGrid: List[List[int]]
        :rtype: int
        """
        
        if obstacleGrid[0][0]==1:
            return 0
        
        m=len(obstacleGrid)
        n=len(obstacleGrid[0])
        dp=[[0]*n for _ in range(m)]

        for i in range(m):
            for j in range(n):
                if i==0 and j==0:
                    dp[i][j]=1
                    continue
                if obstacleGrid[i][j]==1:
                    dp[i][j]=0
                else:
                    if i==0 and j>0:
                        dp[i][j]=dp[i][j-1]
                    elif i>0 and j==0:
                        dp[i][j]=dp[i-1][j]
                    else:
                        assert i>0 and j>0
                        dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[-1][-1]
        

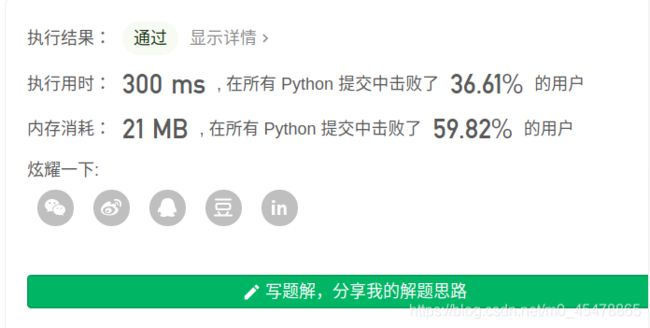
最长公共子序列

两个字符串s1,s2之间的最长公共子串长度是：
if s1[-1]==s2[-1]:
    最长长度=1+(s1[:-1]和s2[:-1]之间的最长公共子串的长度)
if s1[-1]!=s2[-1]:
    当两个字符串最后一个字符不同时
    比较s1[:-1]和s2之间的最长子序列长度以及
        s2[:-1]和s1之间的最长子序列长度
    取两者较大值

class Solution(object):
    def longestCommonSubsequence(self, text1, text2):
        """
        :type text1: str
        :type text2: str
        :rtype: int
        """

        m=len(text1)
        n=len(text2)
        dp=[[0]*(n+1) for _ in range(m+1)]
        #第一行和第一列都是0
        for i in range(1,m+1):
            for j in range(1,n+1):
                if text1[i-1]==text2[j-1]:
                    dp[i][j]=1+dp[i-1][j-1]
                else:
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1])

        return dp[-1][-1]

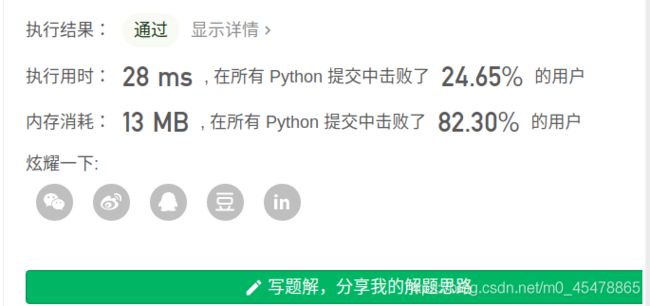
最长公共前缀

直观的思想是：比较其中的两个字符串，它们之间的前缀的长度的最小值就是最长公共前缀。
假设数组有n个字符串，那么比较次数是n次，假设所有字符串的长度的平均值是k，那么时间复杂度是n*k

或者采用二分查找的方式，low=0,high=最短的字符串的长度
然后比较所有字符串的low到middle之间的字符串是否一致，一致则low=middle+1
否则说明前半部分已经存在不匹配的问题，则high-middle-1

def isCommon(low,middle,high,strs):
    string=strs[0][low:middle+1]
    for str_other in strs[1:]:
        if str_other[low:middle+1]!=string:
            return False
    return True

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """

        if len(strs)==0:
            return ''
        if len(strs)==1:
            return strs[0]
        
        # string=strs[0]
        # num_same=200
        # for str_other in strs[1:]:
        #     s=0
        #     while s
        #         s+=1
        #     if s
        #         num_same=s

        # assert num_same<200
        # return string[:num_same]
		
		#注释的代码是第一种直观的解法，用来比较所有字符串最短的前缀长度
		#下面的代码是二分查找
        min_len=min([len(str_) for str_ in strs])
        low=0
        high=min_len-1

        while low<=high:
            middle=(high+low)//2
            if isCommon(low,middle,high,strs):
                low=middle+1
            else:
                high=middle-1
        
        return strs[0][:low]

剑指 Offer 49. 丑数

最简单的想法：按照题意，判断一个数是不是丑数，那么就看这个数是否只包含2,3,5。也就是能否被2,3,5除尽，然后一直遍历，直到累计丑数的数量达到n

def isUgly(n):
    while n%2==0:
        n=n//2
    while n%3==0:
        n=n//3
    while n%5==0:
        n=n//5
    return n==1

class Solution(object):
    def nthUglyNumber(self, n):
        """
        :type n: int
        :rtype: int
        按照题意，判断一个数是不是丑数，那么就看这个数是否只包含2,3,5
        也就是能否被2,3,5除尽
        """
        ugly_number=1
        i=1
        while ugly_number<n:
            i+=1
            if isUgly(i):
                ugly_number+=1
        return i

但是时间复杂度过高，因为每一个数字都要按照规则判断是不是丑数，而这个规则是很耗费时间段。最后超时。