2.算法-贪心算法,分配问题(leetcode455发饼干,135发糖果),区间问题(435无重叠区间),练习(605种花,452射气球,122 买卖股票)
一 算法解释
保证每次操作都是局部最优,局部结果互不相干,全局结果是局部结果的简单求和,从而使最后得到的结果是全局最优的。
二 分配问题
例1:leetcode题455,分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。

1.题目分析:
从胃口小(数组g中最小的)的开始分配,在饼干里找能满足其胃口的且最小的(即数组中大于g【i】且最小的)分给他,然后再考虑剩下的。
贪心策略:每次给剩余孩子里胃口最小的分配能满足胃口的最小饼干
2.优化:
由于两个数组都需找出最小的,且需获得大小关系,如果直接循环遍历两次,容易一开始取到胃口最大的小孩,所以应在开始判定之前,将两个数组都由小到大排序。这样 就可以从头开始分别遍历。
然后这里如果用双层for 的话,情况会很复杂,首先两个数组谁长谁短,每个循环何时结束?都不好判断,而且可能会重复遍历。
所以这个题目用while(numchild
然后符合情况的numchild++,否则就一直numcookie++
3.sort()排序函数:
sort(first_pointer,first_pointer+n,cmp)
3.2 功能:该函数可以给数组,或者链表list、向量排序。
3.3 实现原理:sort并不是简单的快速排序,它对普通的快速排序进行了优化,此外,它还结合了插入排序和推排序。系统会根据你的数据形式和数据量自动选择合适的排序方法,这并不是说它每次排序只选择一种方法,它是在一次完整排序中不同的情况选用不同方法,比如给一个数据量较大的数组排序,开始采用快速排序,分段递归,分段之后每一段的数据量达到一个较小值后它就不继续往下递归,而是选择插入排序,如果递归的太深,他会选择推排序。
3.4参数:
此函数有3个参数:
参数1:第一个参数是数组的首地址,一般写上数组名就可以,因为数组名是一个指针常量。
参数2:第二个参数相对较好理解,即首地址加上数组的长度n(代表尾地址的下一地址)。
参数3:默认可以不填,如果不填sort会默认按数组升序排序。也就是1,2,3,4排序。也可以自定义一个排序函数,改排序方式为降序什么的,也就是4,3,2,1这样。
3.5使用
使用此函数需先包含:
#include 并且导出命名空间:
using namespace std;
简单例子:对数组A的0~n-1元素进行升序排序,只要写sort(A,A+n)即可;对于向量V也一样,sort(v.begin(),v.end())即可。题目中给的是两个向量gs,所以我们使用向量排序。
![]()
4.代码
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());//排序
sort(s.begin(),s.end());
int numchild=0;
int numcookie=0;
while(numchild<g.size() && numcookie<s.size() )//一旦有一个结束就结束
{
if(g[numchild]<=s[numcookie]) numchild++;
numcookie++;//不管孩子吃没吃,饼干始终只能用一次,因为吃的了的话饼干没了得到下一块饼干,吃不了的话上一个胃口小的孩子吃不了下一个胃口大的孩子更吃不了。
}
return numchild;
}
};
5.总结:
1.在开始判定之前,先对数组和字符串进行排序是常见操作,方便之后大小比较。
2.若对连续空间变量进行操作,不区分数组和字符串,因为其本质上都是在连续空间上的有序变量集合。字符传“zfc”可以被看成数组【‘z’,‘f’,‘c’】
例2:135.分发糖果
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?

1.题目分析
1.1
每个孩子至少分配到1个糖果,所以n个孩子至少一开始数目就是n。
1.2
首先明确这个问题没有办法先排序,因为学生的站位会影响到糖果数目。接下来是两侧的问题,我们可以考虑把两侧分开来考虑:
第一次for,从头开始,如果右大于左,则右加一
第二次for,从尾开始,如果左大于右,则左加一
(那么这样说的话如果只有一个人,或者没有人,不需要遍历,直接返回.size()即可)
2.优化
一开始我的思路,在加一方面草率了,不能单独设置一个num一直加,应该给每个小孩都设置一个属性值,一开始都设置为1,第一次从左往右的时候,如果右大于左,右应该等于左+1,意思就是第一次从左往右应该变成一个越阶的升序12312或者112312这种。
但是从右往左的时候,这个num的数值不能简单的自加(可能出现有个值被多加一),要考虑他是不是已经比两边的大了,应该在
他本身 和 他右边值+1 里面取max。
3.代码
class Solution {
public:
int candy(vector<int>& ratings) {
int num=ratings.size();
vector<int>f(num,1);
int sum;
if(num<2) return num;
for(int i=0;i<num-1;++i)
{
if(ratings[i+1]>ratings[i])
f[i+1]=f[i]+1;
}
for(int j=num-1;j>0;--j)
{
if(ratings[j-1]>ratings[j])
f[j-1]=max(f[j-1],f[j]+1);
}
sum=accumulate(f.begin(),f.end(),0);
return sum;
}
};
三 区间问题
例:435无重叠区间
435.给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。

分析:
首先,对于每个区间来说,我们先考虑它的结尾,如果第一个区间的结尾尽可能的小,那么我们留给后面区间的空间就大,也就是说需要移除的区间应该最小。因此,我们有限考虑保留结尾小,且不相交的区间。
优化:
可以先对每个区间进行按结尾升序排序(如果区间结尾相同那就把区间开头小的放前面),这个跟我们第一个发饼干的思路一样。这样第一个就是结尾最小的,之后我们每次选择结尾最小的和前一个被选择的比较以下有没有重叠,如果有,就移除的num++,如果没有就继续。
验证一下示例:
示例1: [ [1,2], [2,3], [3,4], [1,3] ]
1.先排序,应该得到这样的二维数组 [ [1,2], [1,3] [2,3], [3,4] ]
2.看第二个【1,3】和第一个【1,2】有没有交集,后一个数组的1比前一个数组的2小,所以有交集,【1,3】要去掉。
3.【2,3】,【3,4】均无交集。
示例2: [ [1,2], [1,2], [1,2] ]
1.先排序 [ [1,2], [1,2], [1,2] ]
2.第二个1小于第一个2,有交集,同理,去掉后两个
示例3: [ [1,2], [2,3] ]
1.先排序 [ [1,2], [2,3] ]
2.均无交集。
注意:
1.sort()函数,默认的是对二维数组按照第一列的大小对每行的数组进行排序。如何进行排序,这里有一篇写的非常清楚的文章。sort排序
sort(intervals.begin(),intervals.end(),[](vector<int>a, vector<int>b)
{
return a[1]<b[1];
}
);
这样我们就可以是实现按每个区间的结尾升序排列。
代码:
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals)
{
int s=intervals.size();
if(s<2) return 0;
sort(intervals.begin(),intervals.end(),[](vector<int>a, vector<int>b)
{
return a[1]<b[1];
});
int num=0;
int q2=intervals[0][1];//第一行第二个
for(int i=1;i<s;++i)
{
if(intervals[i][0]<q2)
++num;
else
q2=intervals[i][1];
}
return num;
}
};
四 练习
题一:605.种花问题
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。
另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。

分析:
n如果=0,一定能种下。
首先明确花坛里能种n朵花是一个偶然情况,不能种这么多花才是一般情况,所以只需要考虑如何能种下n朵花,其他情况均为false即可。
我们从头开始遍历flowerbed数组,判别每个flowerbed【i】分两种情况:
1.如果是1,表明此处有一朵花,i向右移动2(i+2)
2.else如果是0,判别flowerbed【i-1】和flowerbed【i+1】是不是也是0:
2.1如果都是0,那么此处可以种花,n–,i+2;
2.2else,此处种不了花,i++;
最后,看f是不是>=n即可;
优化:
怎么处理边界问题:
在第一个元素前面和最后一个元素后面,都插入一个0,这样每次判定都可以判定连续三个数是不是0即可,不需要分头尾的情况。
代码:
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
flowerbed.insert(flowerbed.begin(),0);//左右各加个盆,避免边界情况
flowerbed.insert(flowerbed.end(),0);
int s=flowerbed.size();
if(n==0) return true;//n如果=0,一定能种下。
for(int i=1;i<s-1;i++)
{
if(flowerbed[i]==1) i++;//如果此处已经有花,直接右移2
else
{
if(flowerbed[i-1]==0 && flowerbed[i+1]==0)
{
n--; //种一朵
i++;//右移2
if(n==0)
return true;
}
//else右移1
}
}
return false;
}
};
题二:42 射气球问题
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
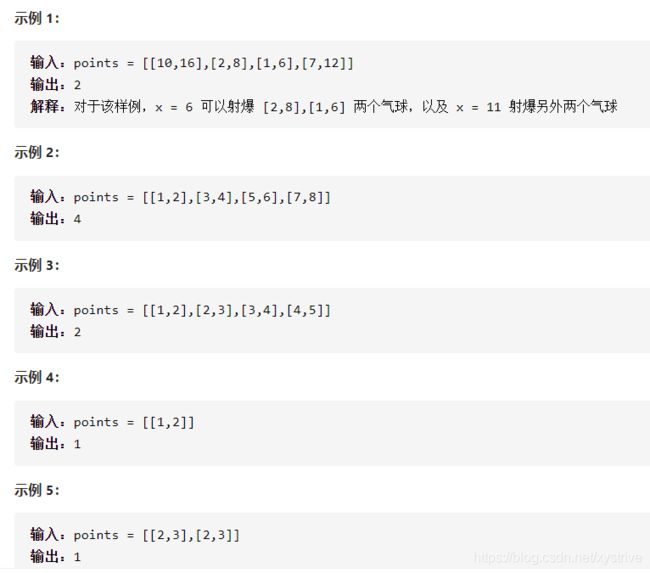
注意:两个边界挨着的,可以同时引爆
示例分析:
示例1:points = [[10,16],[2,8],[1,6],[7,12]]
1.对其进行按结尾升序排列newpoints = [[1,6],[2,8],[7,12],[10,16]]
2.从【1,6】开始,num=1,pre=6;
【2,8】和前有重叠,2<=6,num不变,设置【2,6】为雷区,i++
那么第三个区间有以下可能性:
区间3的第一个数如果也<=6,num不变,i++
区间3的第一个数如果>6,num++,i++,pre=…
所以【7,12】中,7>6,num++,i++,pre=12;
【10,16】和前有重叠,num不变,结束
示例2:points = [[1,2],[3,4],[5,6],[7,8]]
1.升序排列newpoints = [[1,2],[3,4],[5,6],[7,8]]
2.从【1,2】开始判断,num=1,pre=2;
【3,4】无重叠,num++,i++;pre=4;
【5,6】无重叠,num++,i++,pre=6;
【7,8】无重叠,num++,i++;结束num=4;
示例3:points = [[1,2],[2,3],[3,4],[4,5]]
1.升序排列newpoints = [[1,2],[2,3],[3,4],[4,5]]
2.从【1,2】开始,num=1,pre=2;
【2,3】2<=2,有重叠,num不变,设置【2,2】为雷区,i++
【3,4】3>2,无重叠,num++,i++,pre=4;
【4,5】4<=4,有重叠,num不变,结束。
示例4:points = [[1,2]]
points.size()<2, return points.size();
示例5:points = [[2,3],[2,3]]
1升序排列不变
2.从【2,3】开始,num=1,pre=3;
【2,3】有重叠,2<=3,num不变,结束;
总结就是
先升序排列,预参数设置好。然后开始for循环。如果有重叠,则不操作,无重叠则 num++,pre更新;
代码:
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
int s=points.size();
if(s<2) return s;
sort(
points.begin(),points.end(),[](vector<int>a,vector<int>b)
{
return a[1]<b[1];
}
);
int num=1;
int pre=points[0][1];
for(int i=1;i<s;++i)
{
if(points[i][0]>pre)//无重叠
{
num++;
pre=points[i][1];
}
}
return num;
}
};
题三:122 买卖股票
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。

分析:
股票无非就涨和跌两种情况,现在我们属于一种先知的情况:
最开始,买不买股票,取决于第二天是涨还是跌。如果第二天涨,那我们第一天买,如果第二天跌,则不买。
需要明确,如果他第三天连涨,我们没有必要每天都买卖,直接持有到他下跌为止。
示例分析:
示例1:[7,1,5,3,6,4]
7>1,第一天不买,i++(因为第二天跌了)
1<5,第二天买,num=-1(因为三天涨了,且手里没有买入的)
5<3,第三天卖出,num=5-1=4(因为第四天跌了)
3<6,第四天买入,num=4-3=1(因为第五天涨了)
6<4,第五天卖出,num=6+1=7(因为第六天跌了)
第六天是最后一天,手上没有股票,结束;
优化:
这个循环不需要从第一天跑到最后一天,由于我们是先知,我们从第一天跑到倒数第二天即可。
每一天预知第二天上涨的话,利润就加上差额。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int s=prices.size();
int num=0;
int flag=0;
for(int i=0;i<s-1;++i)
{
if(prices[i+1]>prices[i]) //明天上涨,今天就提前有利润
{
num+=prices[i+1]-prices[i];
}
}
return num;
}
};