详解KMP算法

---

串的存储结构

#define MAXLEN 255
typedef struct
{
     
	char ch[MAXLEN+1];
	int length;
}SString;

结构由一个字符数组和代表长度的length组成

---

一、BF算法

目的：从S中匹配子串T，并返回第一个匹配字符的位置
实现：这是最简单直观的模式匹配算法
①从两个串逐个字符相匹配，如果相同继续匹配，不同则S串指针退回到上一次匹配的下一位，T串指针退回到首位，继续匹配。
②最后当j>T.length则说明匹配成功，返回当前S串的i-T.length即为第一个匹配字符的位置

int Index_BF(SString S,SString T,int pos)
{
     
	int i=pos,j=1;
	while (i<=S.length&&j<=T.length)
	{
     
		if(S.ch[i]==T.ch[j]) {
     ++i;++j;}
		else {
     i=i-j+2;j=1;}
	}
	if(j>T.length) return i-T.length;
	else return 0;
}

若S串为“abcababca”,T串为“abcabx”

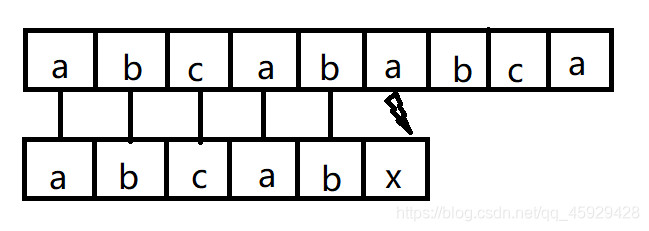
当T串末位‘x’与主串’a’不匹配时，T串整体向后移动继续匹配

当T串末位‘x’与主串’b’不匹配时，T串整体向后移动继续匹配
直到匹配完成为止，此样例无法匹配完成，

---

二、KMP模式匹配算法

目的：从S中匹配子串T，并返回第一个匹配字符的位置
实现：这是提高效率的模式匹配算法
①从两个串逐个字符相匹配，如果相同继续匹配，不同则S串指针i不回溯，将next[j]=j将当前位置的next数组值赋给j，继续匹配。
②最后当j>T.length则说明匹配成功，返回当前S串的i-T.length即为第一个匹配字符的位置

int Index_KMP(SString S,SString T,int pos)
{
     
	int i=pos,j=1;
	int next[MAXLEN];
	get_next(T,next);
	while (i<=S.length&&j<=T.length)
	{
     
		if(j==0||S.ch[i]==T.ch[j]){
     ++i;++j;}
		else j=next[j];
	}
	if(j>T.length) return i-T.length;
	else return 0;
}

若S串为“abcababca”,T串为“abcabx”

如图，当T串末位‘x’与主串’a’不匹配时
观察T串第一个字符’a’与第二三个字符bc不同，而S串第二三个字符与T串二三个字符相匹配，所以直接跳过T串首字符’a’与S串第二三个字符的比较

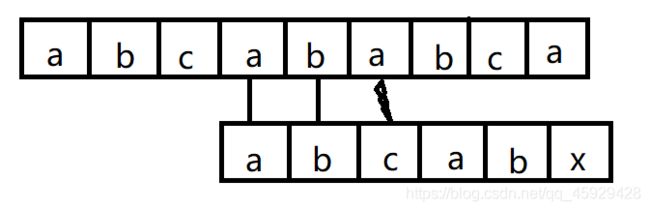
因为T串前两个字符ab和T串第四五个字符ab相同，而第四五个字符已经与S串第四五个字符相比较匹配，所以也可以跳过

此时j=3，直接从T串第三个字符开始比较。
KMP算法避免了BF算法中多余的“回溯”，大大避免重复遍历的情况

求next数组的值

下面来看一看如何得到next数组：
通过上面的例子可以看出，next数组的值与S串无关，只与T串本身的结构有关。
我们把T串各个位置的j值的变化定义为一个数组next，那么next的长度就是T串的长度，我们可以得到定义：

void get_next(SString T,int next[])
{
     
	int i=1,j=0;
	next[1]=0;
	while (i<T.length)
	{
     
		if(j==0||T.ch[i]==T.ch[j]){
     ++i;++j;next[i]=j;}
		else j=next[j];
	}
}

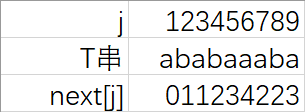
当j=1时next[1]=0
当j=2时next[2]=1
当j=3时next[3]=1
当j=4时，前三位前缀后缀都是‘a’,所以next[4]=2
当j=5时，前四位前缀后缀都是‘ab’,next[5]=3
当j=6时，前五位前缀后缀都是‘aba’,next[6]=4
当j=7时，前六位前缀后缀都是‘a’,next[7]=2
当j=8时，前七位前缀后缀都是‘a’,next[8]=2
当j=9时，前八位前缀后缀都是‘ab’,next[9]=3

---

三、KMP模式匹配算法改进

int Index_KMP(SString S,SString T,int pos)
{
     
	int i=pos,j=1;
	int next[MAXLEN];
	get_nextval(T,next);
	while (i<=S.length&&j<=T.length)
	{
     
		if(j==0||S.ch[i]==T.ch[j]){
     ++i;++j;}
		else j=next[j];
	}
	if(j>T.length) return i-T.length;
	else return 0;
}

KMP算法存在一定的缺陷
例如当S=‘aaaabcde’，T=‘aaaaax’时
T的next数组值分别为012345，当匹配i=5、j=5时，发现b与a不相等，因此j=next[5]=4,仍然不等j=next[4]=3…以此类推直到j=next[1]=0,此时i++、j++，得到i=6、j=1,继续向后匹配。
我们可以发现其中的步骤可以省略，T串中a与后四个字符均相等，我们可以用首位的next[1]的值取代后续字符next[j]的值。

求nextval数组的值

void get_nextval(SString T,int nextval[])
{
     
	int i=1,j=0;
	nextval[1]=0;
	while (i<T.length)
	{
     
		if(j==0||T.ch[i]==T.ch[j])
		{
     
			++i;++j;
			if(T.ch[i]!=T.ch[j])nextval[i]=j;
			else nextval[i]=nextval[j];
		}
		else j=nextval[j];
	}
}

当j=1时next[1]=0，nextval[1]=0
当j=2时next[2]=1,第二位字符的next值为1,第一位为a,b与a不同，所以nextval[2]=next[2]=1
当j=3时next[3]=1,第三位的字符next值为1,第一位为a,相同，所以nextval[1]=nextval[1]=0
当j=4时next[4]=2,第四位的字符next值为2,第二位为b,相同，所以nextval[1]=nextval[2]=1
当j=5时next[5]=3,第五位的字符next值为3,第三位为a,相同，所以nextval[5]=nextval[3]=0
当j=6时next[6]=4,第六位的字符next值为4,第四位为b,a与b不同，所以nextval[6]=next[6]=4
当j=7时next[7]=2,第七位的字符next值为2,第二位为b,a与b不同，所以nextval[7]=next[7]=2
当j=8时next[8]=2,第八位的字符next值为2,第二位为b,相同，所以nextval[8]=nextval[2]=1
当j=9时next[9]=3,第九位的字符next值为3,第三位为a,相同，所以nextval[9]=nextval[3]=0

改进后的KMP算法，是在计算出next值的同时，如果a位字符与它next值指向的b位字符相等，则该a位的nextval就和b位的nextval相等；
如果不等，则该a位的nextval值就是它自己的next的值。

---

总结

本篇介绍了串的结构和匹配模式算法，并介绍了优化的KMP算法

测试代码及运行实例

int main()
{
     
	SString cr,me;
	cr.length=10;
	for (int i = 1; i <= cr.length; i++)
	{
     
		cr.ch[i]=i+64;
		cout<<cr.ch[i];
	}
	cout<<endl;
	me.length=5;
	for (int i = 1; i <= me.length; i++)
	{
     
		me.ch[i]=i+69;
		cout<<me.ch[i];
	}
	cout<<endl;

	cout<<Index_BF(cr,me,1)<<endl;
	cout<<Index_BF(cr,me,1)<<endl;
	cout<<Index_KMP(cr,me,1);
	return 0;
}