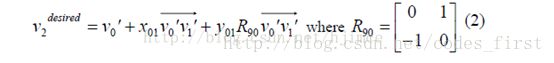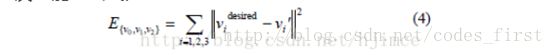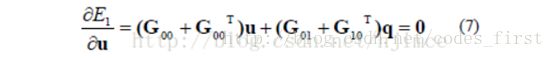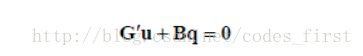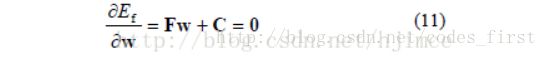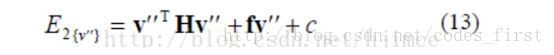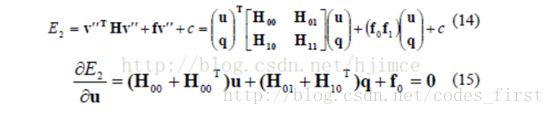As-Rigid-As-Possible Shape Manipulation论文笔记

这篇博客我会结合自己做的presentation对一篇siggraph上一篇古老但十分重要的论文As-Rigid-As-Possible Shape Manipulation做个介绍。有好几篇后来的siggraph上的文献，在视屏防抖《Content-Preserving Warps for 3D Video Stabilization》为三维视频稳定提供内容保护的空间扭曲《Bundled Camera Paths for Video Stabilization》为视频稳定捆绑了相机路径，还是在图像全景《Rectangling Panoramic Images via Warping》通过扭曲的矩形全景图像等都用到这个算法，

首先说一下大致介绍一下摘要说的重要的内容：

提出一个互动的系统,让用户移动和变形的二维图形，不需要事先手动建立骨架或自由变形(FFD)。图形是建立在一个三角形网上，用户移动几个约束顶点变化。然后系统通过最小化每个三角形的变形误差计算剩余自由顶点的位置。

在基于物理的模拟或迭代改进还可以用于这个目的,他们往往是缓慢的。我们提出一个两步封闭算法,实现实时交互。第一步找到一个适当的旋转和移动，第二步调整规模。

主要方式是使用二次误差度量以便每个最小化问题成为一个线性方程组。解联立方程后开始互动,我们可以很快找到自由的顶点的位置在交互式操作。

方法成功地传达了一种刚性的形状,在空间变形方法是困难的。多点输入设备,即使是初学者可以很容易地移动,旋转和变形形状。

所以，这篇文章的大致思路就是：

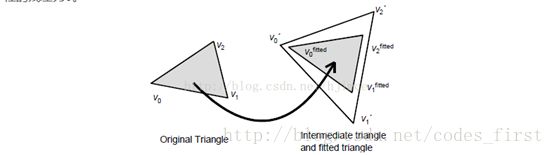
设计一个二次误差度量的自由变量的系统可以解决最小化问题作为一个简单的矩阵计算。理想情况下,希望一个适当的二次误差函数代表整体变形。在检查了各种可能性后,最后得出的结论是,它是不可能设计这样一个功能。我们的解决方案是将问题分割成一个旋转部分和规模部分,每个部分由一个独立的二次误差函数。这种分解,我们可以获得最终结果按顺序解决两个最小二乘问题。给定约束顶点的坐标,第一步生成一个中间结果通过最小化错误指标,防止剪切和不均匀拉伸但允许旋转和统一的扩展。第二步需要这个结果和调整每个三角形的规模。第二步是进一步分解为两个连续的过程。系统首先符合每个原始三角形对应的中间三角形不改变规模,然后计算最终结果通过最小化错误度量表示安装三角形之间的差异以及由此产生的三角形。

相关工作：

先介绍一个相关理论的大概念。形状操纵技术大致可分为两类。一个是变形的空间目标形状是嵌入;另一种是变形的形状,同时考虑到其结构。

 

使用骨架变形、FFD和其他空间变形方法属于第一类。骨骼,每一个点的形状是关联到一个坐标系定义的骨头(Lewis et al . 2000]。在FFD,每个点与一个封闭地区FFD网格[MacCracken和喜悦1996]。其他空间变形技术变形全球空间(迪莉娅·米莉蓉et al . 2002年)。贝尔和尼利使用空间变形变形[1992]。捻线机变形全球空间据两位6自由度控制[骆驼et al . 2003],巴雷特和切尼[2002]用于数字图像编辑空间扭曲变形。Brookstein[1989]利用薄板样条函数找到空间变形所定义的一些控制点。这些方法的一个缺点是它们的刚度模型周围的空间,而不是形状本身,因此所产生的变形大大不同于真正的对象的行为。

 

第二类包括物理方法为基础,其中最受欢迎的是弹簧质点模型[吉布森和Mirtich 1997]。这些都是非常容易实现的,但是他们的行为太有弹性了,许多应用程序和收敛缓慢。此外,注意优化各种参数需要让他们真正的工作。身体与有限元方法准确模拟是可能的(Celniker和Gossard 1991),但这些都是非常复杂和昂贵的解决,使他们不适合互动操作简单的图纸。ArtDefo系统(1999年詹姆斯和Pai)实现身体准确、互动形状变形使用边界元方法,但它仅限于很小的变形,如戳表面,并不适用于大变形弯曲手臂。

 

这里介绍的工作属于第二类。我们的目标是介绍内部模型刚度成型操作。然而,而不是使用基于物理的模型,我们使用简单的几何方法类似于一种技术用于(Alexa et al . 2000年)。他们获得一个as-rigid-as-possible形状之间的插值通过计算每个三角形元素的一个刚性变换几何和缝合在一起。同样,我们实现操纵as-rigid-as-possible几何最小化畸变与网格中的每个三角形有关。Sheffer和Kraevoy[2004]介绍类似的变形工具,但使用迭代计算,太贵的交互式操作,特别是当控制顶点迅速行动。

 

我们使用的算法可以看作是拉普拉斯算子的一种变体surface-editing Sorkine等提出的方法。[2004]。他们实现了快速detail-preserving变形通过使用旋转和尺度不变的拉普拉斯算子的坐标。他们还提出了扩展变形形状的拉普拉斯算子回到原来的规模,可以集中精力处理。同样的,我们添加一个scale-preserving初始变形过程的影响。我们表明,这种scale-preservation效应有可能更动态操作比在他们的论文中看到的例子,修复,用户大部分的形状和动作感兴趣的特定区域。

算法：

（1）理论讲解

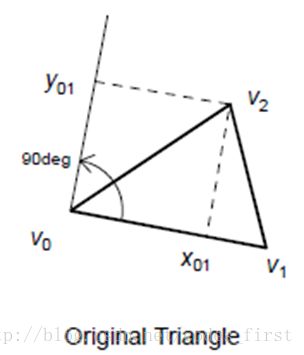
相对坐标的概念：开始这个算法之前，我需要先给讲解一个三角形中相对坐标的概念：给定一个三角形v0v1v2，如下图所示：

                                                       

那么我们定义，v2相对于v0、v1的坐标为(x01,y01)，满足：

                              

也就是说，我们可以通过已知的一个三角形，然后建立一个以三角形的一个顶点为原点，以其邻接边、及其对应的垂直旋转90度后的方向分别作为x轴、y轴，求取三角形另外一个顶点的相对于这个坐标系的坐标。OK，如果我给你一个三角形，我要你计算出(x01,y01)，你要怎么计算？

（x01,y01)表示的是一个相对坐标，如果三角形的三个顶点的坐标已知v0，v1，v2，其实计算这个相对坐标是非常容易的。

(1)建立局部坐标轴。先求出边向量v0v1，然后利用v0v1求出其单位向量即为局部坐标系的x轴，接着只需要把x轴旋转90度，就可以得到y轴了。

(2)计算相对坐标(x01,y01)，这一步首先需要把向量v0v2投影到x轴，y轴。这里需要注意的是我们上面的公式中x轴指的是v0v1，y轴指的是把v0v1旋转90度后的向量，因此我们需要对投影结果做一个缩放处理

相关代码实现如下：

（2）整体保相似

保相似图像变形算法的原理很简单，说白了就是尽量保证变形前后，相对坐标不变，也就是说保证每个三角形的相对坐标(x12,y12)、(x20,y20)、(x01,y01)不变。因为如果两个三角形的这个相对坐标一样，那么这两个三角形就是相似三角形。那么算法具体是怎么实现尽量保证，每个三角形变形前后的这三个相对坐标不变的呢？

 

假设变形后的三角形顶点坐标为v0'，v1'，v2'。因为我们是要尽量的保证相对坐标不变，我们可以根据下面的计算公式：

计算出v2desired，然后使得如下误差最小化：

                                      

                                                          

上面的能量公式越小，就代表变形后的三角形与原三角形越相似。而对于有多个三角面片的网格模型，那么总误差能量公式为：

                                     

这个问题其实归结为求解一个最小二乘问题，大家还记得吗，最小二乘其实就是使得误差能量最小化，因此到了这里其实我们就可以猜到，这个算法最后归结为求解一个稀疏的线性系统。我们的目的是使得上面的总能量最小化，设相对坐标v’=那么：       解线性方程-------》矩阵求

                                         

我们的问题是要使得E1{v’}最小化，而最小化说白了就是使得其偏导数为0，因此我们需要对E1{v’}求偏导。开始前先把公式5，换另外一种形式来表达：

                                 

其中，q表示控制顶点，u表示自由顶点，对上面式子求偏导：

                           

把上面式子简写为：

                                                      

需要注意的是：对于控制顶点不变的模型，G'、B是一个固定的稀疏矩阵，因此我们可以通过上式求解u，得到自由顶点的坐标。

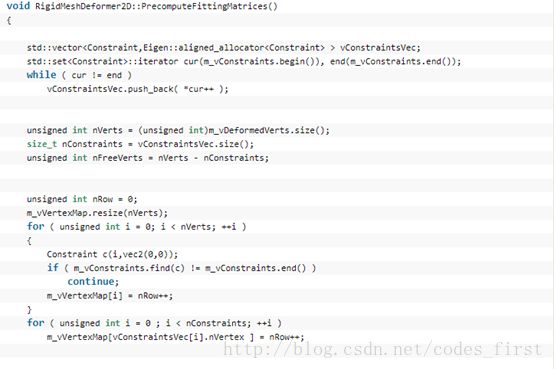
得到约束顶点

初始化矩阵

得到控制顶点和自由顶点的大小

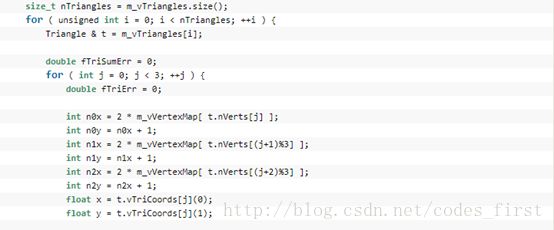
对每个三角面片，得到它的三个顶点的数据和前面计算到的局部相对坐标

通过相应的矩阵计算得到我们的G

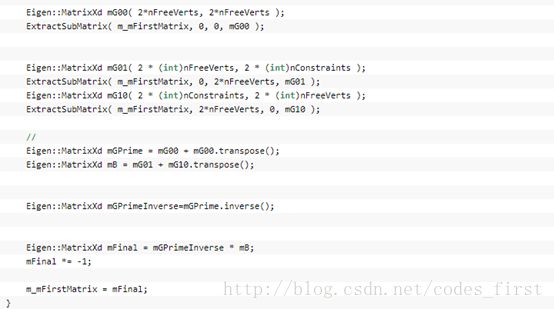
通过G得到G00、F01、G10后，根据之前推导的公式，可以求得G‘-1B

再通过一些后续操作得到自由顶点的坐标。这样我们得到初步的所有三角形的坐标和相对坐标。

（3）局部完全保相似

即局部缩放调整。每个三角形分开重新调整，使得其与原三角形更为相似，同时对其做缩放调整。

首先，在经过上面的整体相似变换后，三角形可能进行放大或者缩小，因为我们用了三角形的内在属性相对坐标，这样只能保证所有三角形的尽量相似，并不能保证全等。如果算法直到这里就结束了，那么变形后的图像将会出现局部放大与缩小。就拿上面的瘦脸图片来说，如果只经过上面相似变换步骤，我们只是要移动脸型轮廓的特征点，而最后变形出来的结果可能就会出现眼睛等局部位置的放大，或缩小，因此我们要进行大小调整，瘦脸后，眼睛的大小与原来图像的大小相等。

                                 

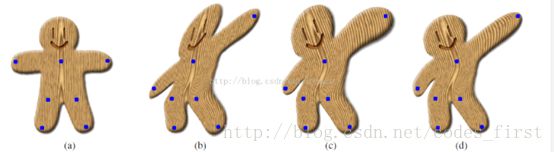
就像上面图像中，图(a)是原图，图(c)的结果就是只经过相似变换后的结果，可以看到(c)中的右手部变粗了许多，而左手部变细了许多，因此我们接着这一步要做的事就是调整大小，使得(a)变形后，使得图像变形后不会出现局部放大与缩小的情况，得到如(d)结果图。

另一方面，在经过上面的整体相似变换后，因为我们用了整个三角网格模型进行整体调整，使得能量最小化，这个就像最小二乘一样，最后求解出来的结果并不能保证每个三角形与原三角形完全相似，也会发生错切变换，误差还是存在的。就像最小二乘，求解出来的结果并不能保证最后每个方程的残差为0.

                                  

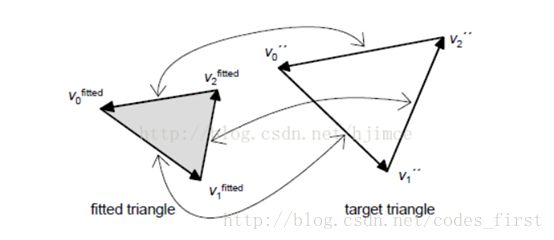
在经过(2)中的相似变换后，因为我们是对网格模型的所有三角形一起调整的，保证总三角形错切变形能最小化，这个时候得到的每个三角形也不全是完全相似的一个三角形，且大小也发生了变化，如上图所示。我们得到了v0'v1'v2'，这个三角形我们称之为中介三角形，接着我们要把每个三角形分开拟合成跟原三角形v0v1v2完全全等的三角形，我们定义拟合阶段的三角形变形能为：

                                

当然我们还需要保证变形前后的也与原三角形相似：

                         

这样联立公式(9)、(10)，同时对其求偏导，使得变形能最小化：

                            

                                                     

记住，这一步是对每个三角形进行分开调整，这样才能得到与原网格模型的三角形完全相似。同时在满是上面式子后，对整个三角形以重心坐标为缩放原点，对每个三角形进行缩放调整

（4）整体拟合

上面那一部是对每个三角形分开调整，这个时候，每个三角形是完全独立的，我们需要对齐对整体连接调整，否则两个邻接三角形的共用边的两个顶点的位置各不一样，这样根本是不是三角网格模型。

                                  

                                       

整个三角网格模型的总能量为：

                                            

H是一个表示整个网格模型拓扑连接关系的矩阵，对上式换另外一种表达方式，并对其求偏导，求取最小值：

                                   

简化为：

                                          

然后重新求解，可得到自由顶点u的坐标。

接下来论文还讲了一些其用到的小trick

1.碰撞检测和深度调整

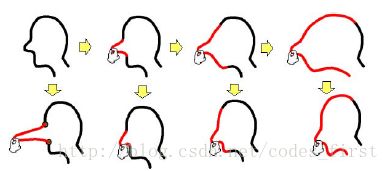
我们必须小心当形状的不同部分重叠。如果我们分配深处不当,重叠部分可以互相渗透(图中)。一个问题是,一个人不能分配静态一致的深度值,适用于所有可能的变形。图显示了一个简单的案例。假设我们有整个形状连续深度值。鉴于三分a、b和c,我们可以假设一个深度< b s深度< c年代深度。如果我们把顶点b和c之间的变形,必须存在一个边缘,有一个顶点比b,另一个是浅深。这会产生不良工件如图所示。

我们的方法是在互动的过程中动态调整深度(图)。我们持续监测selfintersection和分配适当的深度值的网格重叠部分。这个过程类似于隐线消除算法[霍农1984]。我们首先定位边界十字路口然后搜索重叠区域从这些边界的交叉点上。确定的深度顺序重叠区域,仍然是一个悬而未决的问题。我们目前使用静态预定义的订单作为一个起点。我们还实现了一个非常简单的机制来实现帧到帧的连贯性,但它仍处于初步形成

勾结检测和深度调整。没有适当的深度赋值,可以看到渗透(中心)。我们发现重叠区域和调整深度。

2.重量控制刚度

因为我们的算法最小化一个简单的错误功能,添加不同的权重的不同部分网格是非常简单的。这样做是为了控制形状的局部刚度。我们提供一幅画界面中,用户可以比其他的某些部分硬。我们目前使用的重量10000画的三角形,1人。这是有用的在防止重要的特性,比如一头被扭曲(图9)。可以执行完美的刚度降低自由变量最小化,从而获得类似的结果,但是我们发现权重更灵活,并产生更令人愉悦的结果在极端扭曲。

调整刚度重量。通过增加额外的重量 重要的区域，可以防止不良的扭曲。

3.动画

shape操纵技术是有用的在制作二维动画,例如通过设置字符形状在每个关键帧。这是特别有用,当一个人想要动画图纸和详细的表面装饰,因为手动绘制是乏味的。这也使实际变形动画的拍摄对象。

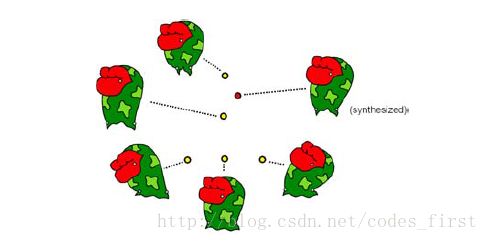
另一种方法是使用动画。同时通过操纵多个控制顶点,一个可以让有趣的动画通过记录现场表演。我们目前正在测试技术类似于非政府组织等人的系统[2000]和面部动画的例子(Lewis et al . 2000]。用户第一次设置一个姿势通过操纵控制顶点和同事控制顶点配置与一个特定的点在画布上。设置几个这样的关键姿势后,用户可以同时直接多个控制顶点通过控制光标移动。系统计算一个适当的控制顶点配置使用径向基函数插值附近的关键姿势。

使用空间设计性能驱动的动画 的知识。用户指定一组关键的姿势(黄色标记) 操作处理。然后他们可以操纵整个身体 拖动控制光标(红色标记)。系统混合了附近的姿势 使用径向基函数。

由此产生的动作非常流畅，因为用户 自己的手运动出现在结果动画中。在 此外，它比传统的时间更容易和更快 使用现有形状变形技术的关键帧。

4.保刚性曲线编辑

我们还将两步算法应用于曲线编辑。为了 曲线编辑，我们采用折线代替三角形网格 输入。我们首先应用二维拉普拉斯曲线编辑[Sorkine等。 然后将我们的规模调整过程应用于结果。 图11显示了一个示例操作。没有规模的调整, 曲线会自由地增长和收缩。随着规模的调整, 曲线的表现就好像它是刚性的。

曲线编辑，无刻度调整程序。 没有规模的调整，伸展的区域就会增长，并被压扁 区域收缩。

让用户调整影响地区的动态交互过程中,我们引入一个剥界面影响的地区随着用户拖了曲线的父亲(图12)。这使用户预先指定地区产生影响,使交互非常直观。作为一个选项,我们还允许用户显式地指定地区的影响通过将虚拟图钉的拖动之前沿着曲线。类似grab-and-pull曲线编辑工具中使用Macromedia Flash,但它只允许本地更改,不让用户改变的影响。具有剥离界面的曲线编辑。当用户拉动 曲线越远，影响区域就越大(从左到右)。用户可以 也要预先显式地指定该区域(左下角)