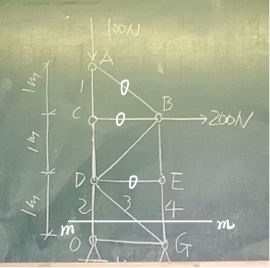理论力学 期末复习

一、知识要点

1. 含销钉的受力分析

1. 二个物体的中间铰处受集中力时，含不含中间处销钉，此处受力分析不同。
   一般而言，含销钉时集中力应画，另外要画另一个物体对销钉作用力（一般二个，二力构件时画一个），只有一个物体含销钉，另一个不含才有作用力与反作用力关系，不含时集中力不画。无集中力时含不含没区别。
2. 三个物体的中间铰，含不含受力图不同(见4)
3. 构件与销钉分离 ，构件会受到来自销钉的力；构件与销钉不分离，构件会受到销钉受到的主动力
4. 销钉与铰支座分离时，铰支座会给含销钉的构件约束力作用（因为与销钉与铰支座分离会受到约束力的作用），而不含销钉的杆件会受到解除销钉而受到的约束力，而这个约束力会给含销钉的杆件一个反作用力

2. 力、力偶(矩)、平面汇交/力偶力系的平衡

1. 力投影正负：与投影轴正向一致为+，反之-。（即标准数学坐标系时，向右向上为正，向左，向下为负）在列力投影平衡方程时+，-号很重要。
2. 力对点的矩的正负：顺负逆正。即右手掌重合力作用线，指尖指向力方向，手指绕向矩心，手指绕向为逆时针钟向为+，反之-。
3. 力偶矩的正负：顺负逆正。右手掌重合一力作用线，手指绕向另一个力，看手指绕向。同2一样，在第三章列矩平衡方程中至关重要。
4. 力偶的最重要性质：力偶只能同力偶平衡或等效（此点可简化固定铰，中间铰约束力）；力偶对任意点的矩等于力偶矩。
5. 平面汇交力系平衡的几何法：要求一物体中力系只能三个力（其中二个未知），受力图必须是真实受力方向。〈判定真实可依力三角形自行封闭或平衡方程思想〉
   注意：箭头与箭头相连表明非真实不能用此法。
6. 平面汇交力系平衡的解析法：画出受力图列力投影（x，y）平衡方程，只能解二个末知数，不必受力图的真实。此法较5适用性更广，一般来说更佳。算出约束力负值表明真实方向与图上假设方向相反，不必修正。
7. 平面力偶系平衡的解析法：各力偶矩代数和为零，只能解一个未知数。算出负值意义同上。按力偶只能与力偶平衡辅助确定约束力方向。

3. 物体系平衡计算要点

1. 选取合适的分离体: 尽量多包含要计算的量,少出现中间末知量;一般来说往往整体可作为一个分离体,而另外的分离体的取法以会出现要计算的反力为原则兼顾简单;
2. 正确完整较简单的分离体受力图,无任是否用到(如对某铰处取矩心,)该处约束力也必画全，主动力必须不简化画出,另外一定要优先判定二力构件,注意作用与反作用关系;
3. 平面任意力系平衡有3个独立方程，可求3个未知数，尽量少联解方程组求解，能一个方程求一个未知数最好;
4. 凡列方程必须有相应受力图,凡方程中出现的约束反力，受力图中必须画有,凡图中从没画出的反力不允许出现于方程中；
5. 合适的矩心与投影轴应使不要计算中间末知量尽可能少出现；
6. 平衡计算原则上宜取尽量少的受力图和尽量少的方程求解,这样可节省时间，也不至于引进错误。

1. 静定问题：独立方程总数=约束力总个数。平衡方程可算全部约束力。
2. n次超静定问题：约束力总数比独立方程个数多n个（n为自然数）。列方程不能全解，但可能解部分分量或一个也解不了。它是更安全的结构，主要可减小内力与变形。
   判定一个物体有几个独立方程必须看是什么力系，平面任意力系3个方程，平面汇交力系2个方程，平面平行力系2个方程。
   计算约束力个数按固定端3个，可动铰1个，连接二个物体的中间铰2个，连n个物体的（含地球）为2（n-1）个。
3. 组合梁是静定结构。一般先分析辅助梁，再分析整体，从而不出现作用反作用关系，不易出错。直接扔掉一物体A，另一物体B能静止，则B为主梁，A为辅梁。也可同时分析主梁，辅梁求解，但要注意作用，反作用，此法一般更差。
   
4. 物体系平衡计算的总原则：（1）选取合适的分离体即使要计算的末知量（约束力）尽量多出现，不需要计算的末知量（中间量）尽量少出现。（2）合适的方程：不要计算的中间量尽量少出现，这往往矩心要合适（尽量多的中间量作用线穿矩心）或投影轴要合适（中间量的作用线与轴垂直的要尽量多）尽量一个方程出一个答案，少联解方程组。此外受力图要注意作用与反作用关系，是否含销钉，矩、力正负正确。

4. 结点法、截面法、零杆的判断

1. 桁架内力计算时，二力构件(直杆)受拉正向假设: 结点法中约束力沿着杆箭头离开结点，算出约束力就等于内力，否则还需用截面法再算。这是计算内力的间接方法。如结点中所连杆不是全部二力构件组合结构，不宜取结点为分离体。
2. 截面法时直接在切开处显示内力，方向为外法向，也叫离开分离体。算出正表示拉，反之压。这是计算内力的直接方法。轴力(拉压变形时的内力)规定为受拉时为正，受压时为负。内力正负号有二个含义:（1）实际方向与真实相同或相反。（2）表示拉伸，压缩。材力，结力中主要强调（2）的含义。
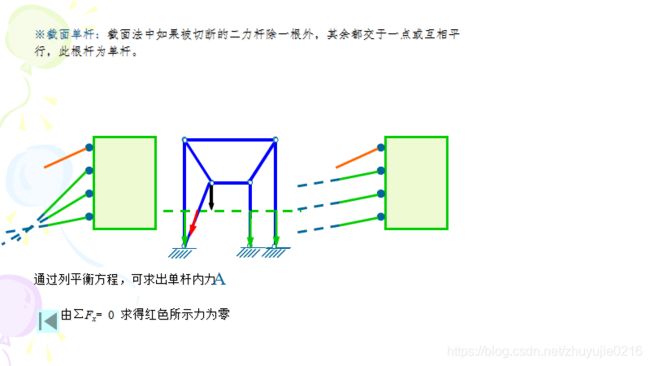
   3.零杆的判定方法有三种情况：（1）二个二力杆连接时不在一条线，结点无外力，二根零杆。（2）三个二力杆连接，结点无外力，不在一条线的杆为零杆。（3）这二杆连接有外力，本质上是（2）的变形，与一力和一杆平行，另一杆为零杆。零杆抗干扰，改变变形方式。
   

5. 摩擦要点

1. 摩擦自锁：主动力合力与法向夹角小于等于摩擦角，物体总是静止。

2. 考虑平衡时的几何法：临界时全约束力与法向夹角等于摩擦角。此法有时特别方便。

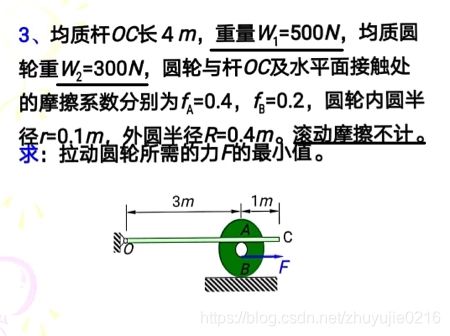
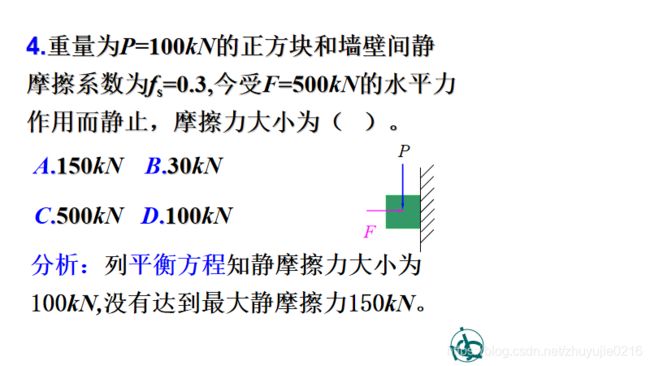
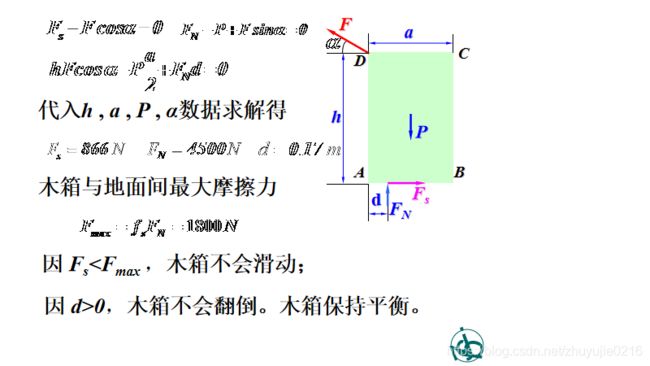
3. 解析法：补充临界时库仑定律，多处摩擦时有时各处末必同时达最大值。（见下面的例题）
   实际静摩擦力不太于理论最大静摩擦力不会滑动；可能翻倒点至法向力作用线距离d>=0，不会翻倒。
   
   
   
   

4. 摩擦力方向与滑动（趋势）相反。
   
   

6. 空间力系要点

1. 力的投影:一般采用二次投影法更方便，与投影轴正向一致为正，反之为负，与轴垂直投影为零。

2. 力对点的力矩矢：定义为位矢叉乘力，可用行列式计算，但用力对轴的矩计算更方便。
   
   也可以用“合力之矩定理”：合力对任一点之矩矢等于力系中各力对该点之矩矢的矢量和
   

3. 力对轴的矩（标量）的计算：一般不用定义式计算，而是用合力之矩定理的第3种形式计算。当分力与轴平行/相交时矩为零。当分力与轴异面垂直时，矩绝对值等于分力大小与异面垂直距离的积，正负号用右手法则定：手重合分力，手指绕向轴，大拇指与轴正向一致为正，反之为负。
   

4. 力偶矩矢（自由矢量）：空间中的力偶可以用力偶矩矢来表示，右手法则定方向，手指绕转向，大拇指方向为矩矢方向。当内力为力偶时，如其力偶矩矢方向平行于轴线发生扭转，扭转时内力（扭矩T）计算按拇指为截面外法向（离开分离体），然后按投影定正负。如其矩矢方向垂直轴线发生弯曲。
   
   上面4个内容中，3，4点最重要！

5. 空间力系合成结果有合力偶，平衡，合力，力螺旋四种情况。
   
   【4(a)的情况可以将M_o转化成两个力，最终合并成一个合力】

7. 点的运动

1. 矢量法推导公式简明。速度是位矢对时间的一阶导数。加速度是速度对时间的一阶导数，是位矢对时间的二阶导数。此法要注意矢量，标量区别。在曲线运动中加速度大小不等于速率的一阶导数。
2. 直角坐标法是计算中大量使用的普通方法，易知轨迹方程。速度投影为运动方程的一阶导数。加速度投影为速度投影对时间的一阶导数，运动方程对时间的二阶导数。此法要求建立坐标系。运动方程可显含时间t，也可隐含时间t，不知初始状态时（或复杂时）后者往往更方便。

8. 刚体的平移和定轴转动要点

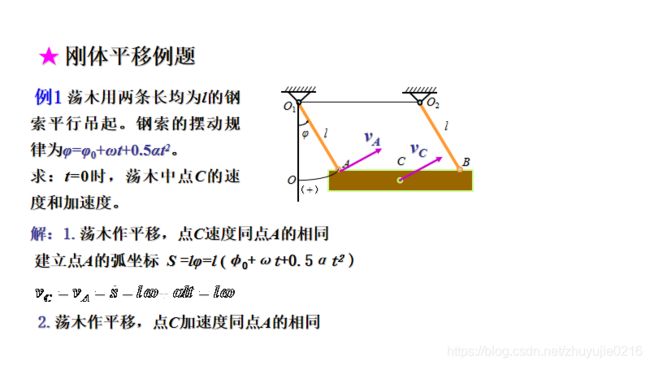
1. 平移(又称平动): 各点速度相同,加速度相同,故第八章如固连于平移列车车箱上的动坐标系上各点速度即为列车速度.
2. 转动:注意转角必须是由坐标轴到任意位置含转向,转角建立不同其导数角速度,二次导角加速正负会不同,故角加速度为正不能表明一定加速转动;
3. 转动刚体上任意点速度必垂直该点与定点连线,顺角速度转向,大小连线距离与之相乘.
4. 转动时任意点加速度有二个分量,法向在连线上指向定点,大小为角速度平方与连线距离的积;切向的垂直连线顺角加速度转向,大小为与距离之积.第8章动系转动时牵连速度V_e方向⊥动点与定点连线依此而定。a_et，a_en也是这样，第9章的类似。
5. 轮系传动比:主动轮角速度与从动轮的之比,与半径或齿数反比.减速目的增大外力偶矩（P=M·ω）。
6. 角速度矢量:右手法则定。第8章科氏加速度要用到。

9. 绝对运动、相对运动、牵连运动

1. 绝对运动：动点在静系中的运动，此时动点的速度为绝对速度==V_a==表示，加速度为绝对加速度，直线运动时为一个，曲线运动时一般有切向，法向二分量。在静止的人看来绝对速度即动点的真实速度。
2. 相对运动：动点在动系中的运动，此时动点相对动系的速度为相对速度==V_r==表示，加速度为相对加速度，一般为一个~二个分量。此运动判定有二种法：法一，想像动系不动，看动点是怎么动的；法二，建立动点相对运动方程来描述。
3. 牵连运动：这不像前二种是动点运动，而是动系的运动。牵连速度V_e不是动系相对静系的速度，而是牵连点相对静系的速度，所以也是一种真实速度。牵连点是动系上的某特定点，在某时刻与动点重合处的点（动点的影子）。动点如选运动平板车上相对有运动的铁球，则任意时刻动点都是铁球，动系固连于车上，则牵连点在每一时刻是不同的点，当铁球滚在车上A点位置时，A点为牵连点，当滚在车上B点时，B点为牵连点。
4. 动系不是一个物体，如上例平板车不是动系而是参照物，固连于参照物上的平移坐标系才是动系。如动系固连于一个运动的点A，点A不是动系，动系是A×’y’平移坐标系。
5. 牵连速度Ve按牵连点真实速度确定。如牵连运动为平移，由平移知识知Ve为平移物体速度。如牵连运动为转动，由牵连点及转动知识知，V_e⊥OM！（O为定轴，M为动点）
   第9章当牵连运动为平面运动，V_e⊥C_vM！（M为动点，Cv为速度瞬心）。

10. 速度合成

1. 绝对速度=相对速度+牵连速度,一般能形成平行四边形,前者一定在对角线上.解平行四边形可算出相关量.前提是大小方向共6个量中必须能确定任四个已知量.否则说明你动点动系不好.有时不能形成平行四边形而是共线，可用投影法*。
   2.动点动系选择原则: 使相对运动为直线或圆周运动 (使相对运动明显),相对运动的判定有二种方法:假设动系不动动点在动系如何动;写相对运动方程来说明.
   3.重点有二个: 一为动点动系的选对;二为正确的矢量合成图(一般为平行四边形)并解之.
   4.此章作业必须指出动点，动系，画速度合成图并解平行四边形，对于高手才允许合成图画矢量三角形否则易错。真实方向确定按va在对角线上。
   5.动点的选取有滑块、销钉、小环一般可选; 接触点有时能有时不能; 圆心一般可以。原则一般要使相对运动为直线运动或圆周运动。
   6.牵连速度由牵连点确定.牵连点是动系上的点与动点位置上重合(即动点的影子)。
   • 当动系固连于一点或平移物体上时，动系是平移系，牵连速度为此固连点或平移物体上的速度。
   • 当动系固连于转动物体时，牵连速度由概念知必然垂直于动点与定轴点的连线。
   • 当动系固连于平面运动物体时，牵连速度必然垂直于动点与瞬心的连线。瞬心是第9章重要概念。

11. 加速度合成

1. 牵连运动为转动时涉及科氏加速度。
   绝对加速度=相对加速度+牵连加速度+科氏加速度。
2. 科氏加速度=2倍的角速度矢量叉乘相对速度，方向用右手法则：右手掌与角速度矢量重合，手指抓向V_r，拇指方向为科氏加速度方向，总是与角速度矢量所在线与相对速度所在线构成的平面垂直。（比如角速度矢是x正向，Vr是y正向，则科氏加速度是z正向）

12. 平面运动

1. 速度分析的基点法本质上是动系固连于基点的合成法。动点B速度V_B(即第8章绝对速度V_a)=基点A速度Ⅴ_A(即第8章牵连速度Ve)+相对基点圆周运动时速度V_BA(即相对速度V_r)。
   速度投影定理由上法推证: 刚体中两点速度在连线上投影相等,此定理 不能计算角速度,但用来判定实际方向很好。
2. 一般从运算简捷而言速度分析的最好方法是速度瞬心法.瞬心指某瞬时速度为零的点,总是与速度丄,分析速度时平面运动可看成绕之瞬时定轴转动.熟练确定瞬心的5种情况，找出瞬心后，第9章的计算相当于第7章。
3. 加速度分析只能用基点法本质上是动系为固连于基点的平移系，相当第八章无科氏加速度的合成。

13. 平面运动时的运动学分析时用什么方法好?

答:
一. 速度分析可以用
(1)基点法:此法要选定基点，动系固连于基点，本质上属牵连运动为平移的合成运动，故要画合成图，合成图不会区分VAB与VBA属严重概念错误，一般而言此法不如瞬心法，尤其要计算多个点时;
(2)速度投影定理，此法不全面，但判定点速度真实方向效果奇好，有时极快;
(3)瞬心法:一般来说，此法最优，且速度瞬心找得到对于写平面运动刚体的动能就简单:对瞬心的转动惯量×角速度平方÷2。
较综合的问题往往要结合合成法，建立动点动系。如牵连运动为平面运动，牵连速度方向必定垂直于动点与速度瞬心连线。

二. 加速度分析的基点法
当平面运动时，一般选定加速度分量方向或大小能确定的点为基点，在动点上进行合成。先将基点A加速度a_A平移画至动点B上，再画由动点B指向向基点A的加速度分量a_BAn，⊥于二点连线的切向分量a_BAt，最后画出动点加速度aB。写出矢量展开式，a_B=a_A+a_BAn+a_BAt，一边看合成图一边投影于合适轴。要区分a_BA与a_AB，前者A为基点，后者B为基点，意义不同。角加速度与a_BAt要协调，均可假设。
注意:所有加速度法向分量方向是确定的，不允许画成反向，其他未知时可假设(只要平行方向对)。

14. 定轴转动微分方程 、平面运动微分方程

1.动量矩计算
2.对定点和质心的动量矩定理及守恒
3.定轴转动微分方程
4.平面运动微分方程
应该说动量矩定理应用主要体现在3,4。作业时尽量使用3，4以不变应万变。
另外含角加速度的微分方程中对点不能乱用,只有以下几种情况可用: (1)定点O (2)质心c (3)加速度为零的点Ca (4)任意时刻与质心距离为常量的速度瞬心Cv。【具体见第17点】
☆对Ca只有角速度为零且二点加速度方向能确定时才能去找，作二加速度垂线，交点为Ca（加速度瞬心）

15. 动静法（达朗贝尔原理）

1. 加上想象的惯性力系后系统形式上平衡从而画合适分离体的受力图列平衡方程计算角加速度，加速度，动约束力等（对任意位置角速度通过积分变换也是可算的）;
2. 平移物体做简化时: 只加惯性力。与加速度方向(或分量)相反，经质心，大小等于质量乘以质心加速度大小。以下提到惯性力均是如此计算。
3. 转动是有二种施加方法: 法一是加惯性力经定轴,方向与质心加速度相反，惯性主矩用对定轴转动惯量乘于角加速度，并与之转向相反; 法二是按平面运动惯性力加于质心,惯性主矩用对质心惯量乘于角加速度，并与之转向相反。一般用法一。
4. 平面运动惯性力只能加于质心,主矩转向与角加速度的反向。
5. 动静法是以不变应万变的方法，在材料力学动载荷，结构力学动力效应及工程应用中大量应用 (此时远好于三大定理的运用)。动静法可独立求角加速度，加速度，动约束力。求角速度，速度也可求但此时不如动能定理快。

16. 常见物体的转动惯量

• 圆柱/圆盘：1/2
• 细直杆：定轴（1/3） 质心（1/12）
• 实心球：2/5

17. 定轴转动时惯性力系的简化

定轴转动可以向定轴，简化也可以向质心
无论向哪一点简化，简化的惯性力都是ma_c，惯性力矩等于J_该点·α
（向任意点简化，惯性力仍为ma_c，惯性力矩不能用J_该点·α 计算，只能利用定轴/质心简化的结论，将力转移到任意一点）

Q：J_质心与定轴不是质心是否矛盾？
A：求J_质心就是把质点当做新的转轴去计算一个值，带入计算得到向质心简化的惯性力矩，与实际转轴到底是什么无关

18. 对线性力系(q)的简化

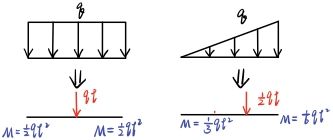
记忆方法：可以想象成一个简化力，大小就等于面积，正方形面积ql，三角形面积ql/2

19. 速度瞬心

1. 特点
   • 瞬时性——不同的瞬时有不同的瞬心
   • 唯一性——某一瞬时只有一个速度瞬心
   • 瞬时转动特性——平面图形在某一瞬时的运动可以看做绕这一瞬时的速度瞬心做瞬时转动
2. 五种情况下的速度瞬心
   
   
   
   
   
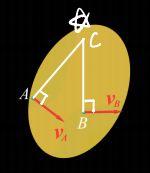
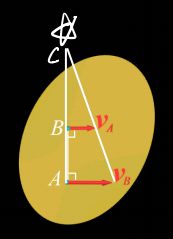
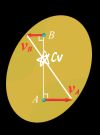
   （瞬时平移：刚体上各点的速度相同，角速度为0，角速度一般不为0）

20. 转动方程的使用限制

只有下面四种情况可以用：

1. 定轴O
2. 质心C
3. 加速度瞬心 Ca
4. 速度瞬心Cv，要求：唯一性，且CCv=常数

21. 平移的特点

1. 刚体上的各点具有形状相同的运动轨迹
2. 刚体上的各点在某一瞬时具有相同的速度和加速度
3. 刚体平移时的运动分析可以简化为其上任意一点(一般取为质心)的运动分析
   

二、 期末复习大纲

幸运提示牌：凡在表达式中出现的参量，图中一定要画出！
一. 判断题：（10题，10分）涉及大纲要求的各章内容；
二. 填空和选择题（9题，23分）涉及大纲要求的各章内容；
三. 计算及画图题（6题67分）

1. 多于4个物体的物体系平衡时约束力计算；
2. 桁架零杆判定，会用结点法，截面法计算内力；
3. 为了某计算目标，指出动点，动系画速度合成图，加速度合成图；
4. 平面运动角速度，角加速度等计算;
5. 动力学普遍定理的应用
6. 动静法计算

三、判断题例题

第一章 基本概念受力分析

• 静力学的研究对象：刚体；材料力学等学科研究对象：变形体（√）
• 理论力学中只研究：外效应，即运动效应（√）
• 力三角形（多边形）法则：共点的力首尾相连，起点到终点的矢量值代表合力（√）
• 作用在刚体上的力—滑动矢量，具有力的可传性（√）
• 当刚体受到同平面内不平行的三力作用而平衡时，三力的作用线必汇交于一点 （√）

---

第二章 平面汇交力系和力偶系

• 只要保持力偶矩不变，力偶必等效（√）

---

第三章 平面任意力系

• 静不定问题是由平衡方程无法求出任意一个未知数（×）
• 桁架空间结构可简化为平面结构

---

第四章 空间力系

• 刚体力对点的矩矢与力的作用点在作用线上的位置有关（×）
  解析：力具有可传性，应该无关
• 力对点的矩矢与矩心O的位置有关（√）
  解析：力对点的矩矢是定位矢量

---

第六章 点的运动学

• 点加速度不变的运动一定是直线运动（×）
  解析：如平抛运动

---

第七章 刚体的简单运动

• 平移是指刚体运动过程中，其上任意直线始终平行于这一直线的初始位置的一种运动

---

第八章 点的合成运动

• 牵连点是在动系上和动点重合的点（√）

---

第九章 刚体的平面运动

• 平面运动刚体的自由度为3（√）

四、选择题例题

第一章 基本概念受力分析

D 要么是汇交力系，不平行，交于一点；要么是平行力系，平行，但不交于一点

C 主矢为0，但是主矩不为0，不平衡，合力不为0

---

第二章 平面汇交力系和力偶系

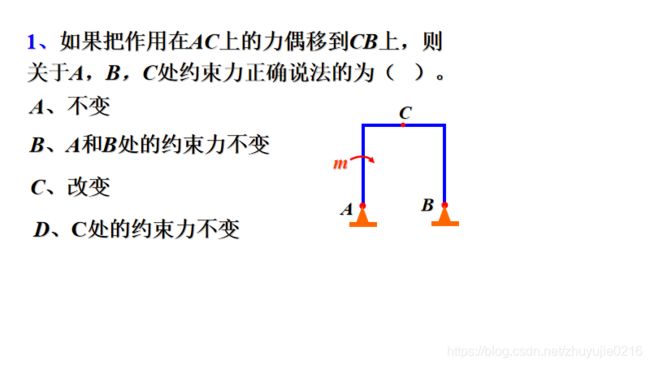
Ｃ　本来BC是二力杆，现在AC是二力杆

C 平面力偶系的作用效果：力偶/平衡；平面汇交力系的作用效果：合力/平衡

---

第三章 平面任意力系

B 注意要分M_o＝0和≠0两种情况

C

C 根据“力偶的等效性”，∑M_A=0和∑M_B=0是一个方程

C 延长AB和DC于O点，对O点取矩

---

第四章 空间力系

B

C 记住结论

D 力是滑移矢量，力对点之矩是固定矢量，力偶矩矢是自由矢量

B 力偶矩矢是自由矢量，不能保证在同一平面内，A错误；三个力偶矩矢的矢量和一定为0 ，所以三个力偶矩矢头尾相连图形必封闭

D

C 如果F₂和F₅的方向换一下，就形成了首尾相连的封闭图形，所以现在五个力的等效结果就是一个力偶，并不平衡，所以需要一力偶来平衡

---

第五章 摩擦

D

有两种情况

D

D

A

B 综合考虑滑动和翻转

---

第六章 点的运动学

B 若是逆时针为正向，则选择D

C 加速度恒矢量，可能是抛物线运动，但不可能是匀变速曲线运动


C

---

第七章 刚体的简单运动

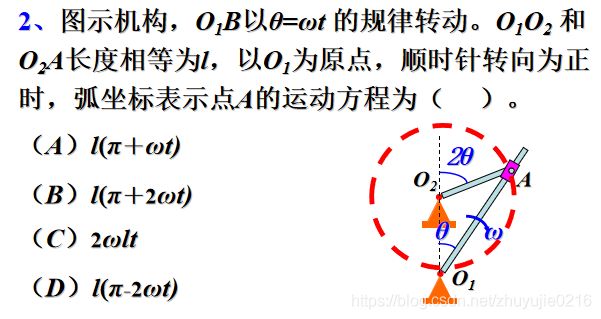
C

D

C 速度方向垂直于AD，加速度方向平行于AD

B

---

第八章 点的合成运动

---

第九章 刚体的平面运动

C




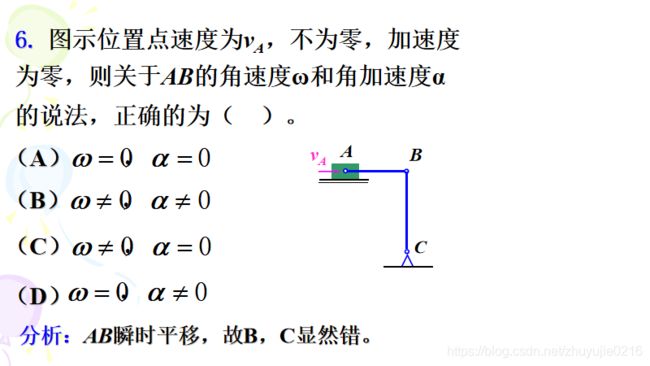
B点只有向下的的加速度，说明BC杆ω,≠0，α=0


瞬时平移，角加速度一般不为0


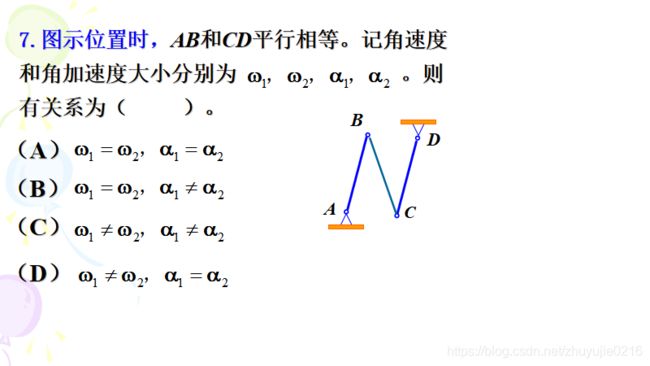
用到了加速度投影定理，记住结论：ω相同，α不相同

五、大题例题

1. 多于4个物体的物体系平衡时约束力计算

例一

例二

1. 先分析整体，列∑F_x=0，得到F_Ax
2. 分析AB，三个独立方程求解三个未知数（F_Ay、F_BDy、F_BDx）
3. 分析整体，列∑M_C=0，得到F_D

例三

此题较简单，三个独立方程，求解三个未知数

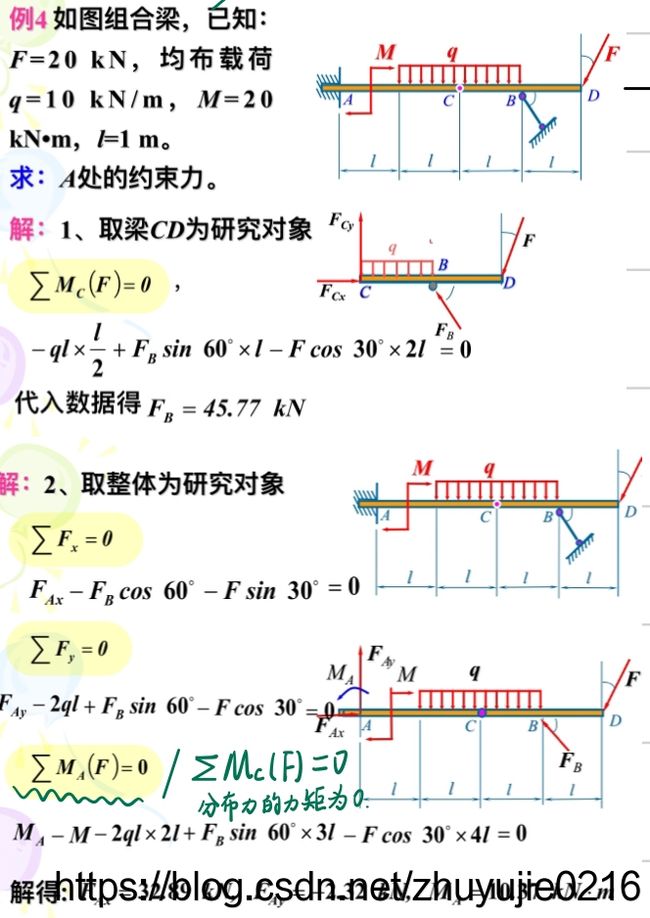
例四

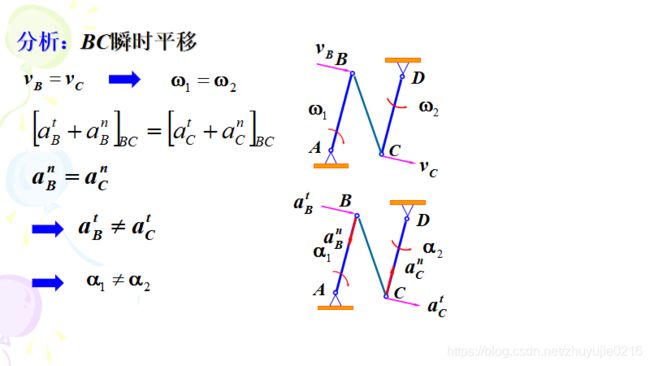
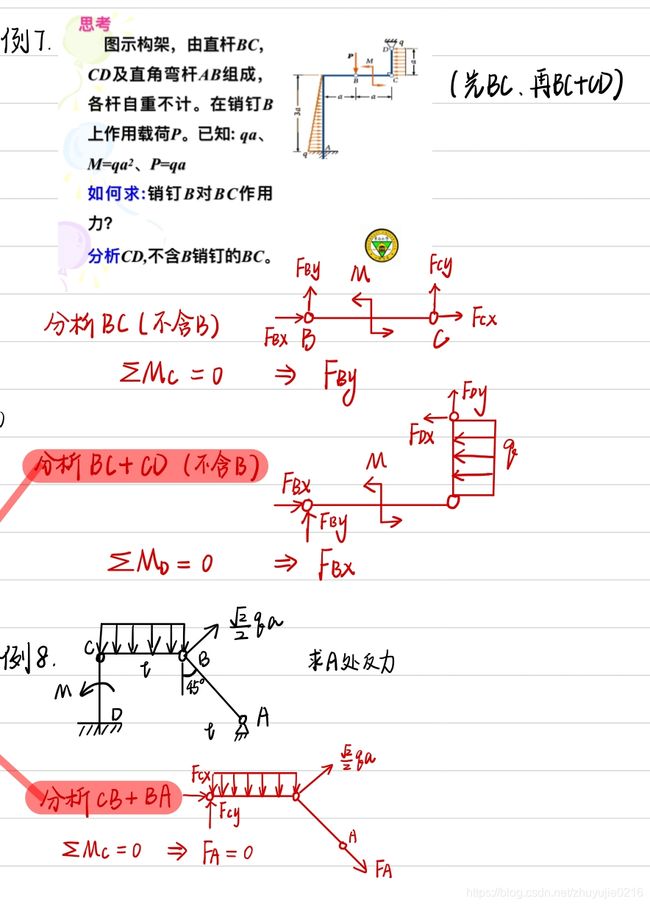
1. 分析BC，列∑M_C=0，得到F_By
2. 分析BCD，列∑M_D=0，得到F_Bx
   （若直接分析BCD，有四个未知数，属于超静定问题，这时候一个也解不了，必须先求解出F_By）

例五

1. 分析整体，分别对A点和D点取矩，求出F_Ax和F_Dx
2. 在y方向上，还缺一个方程就能求出F_Ay和F_Dy：分析AC，为了避免求解F_B和F_C,选定一个新的坐标轴，求出了F_Ay

例六

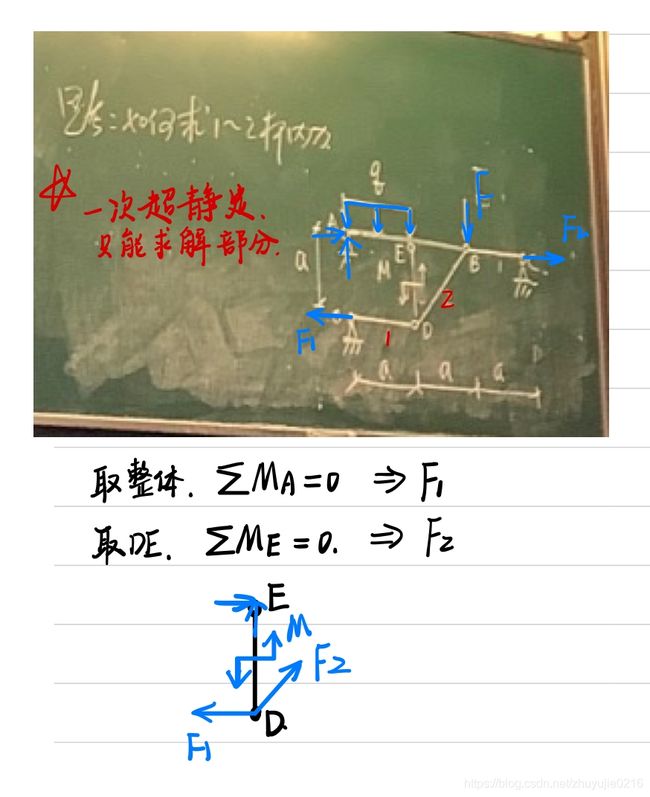
一次超静定，只能求解部分力，分析的对象一定要选好

1. 分析整体，列∑M_A=0，得到F₁
2. 分析DE，列∑M_E=0，得到F₂

2. 桁架零杆判定，会用结点法，截面法计算内力（一定全是二力杆）

注意点：

1. 一句话说明拉压：“计算结果为正，杆件受拉；反之，受压”
2. 计算结果不正好时，保留两位小数
3. 出现g时，用9.8代入
4. 尽量一个式子求解一个力，不然一个错，个个错
5. 一定要先判断零杆，再去求解，会方便很多（题目中也会提示）

例一

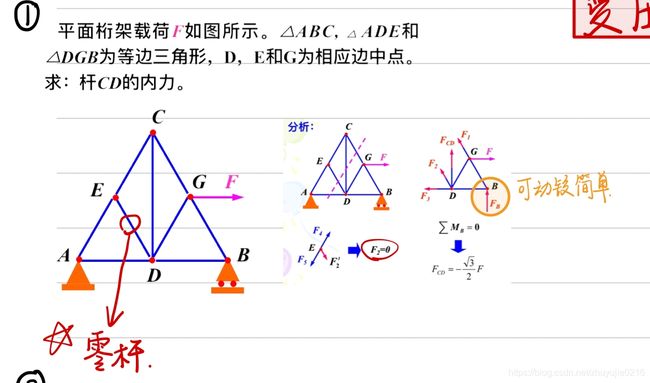
例二

1. 先判断DE是零杆
2. 截面法：考虑到要有所求的量F_CD，零杆DE，就取图示的截面
3. 虽然未知数有四个，但是其他三个不需要求的力交于一点，列矩平衡方程，解出F_CD

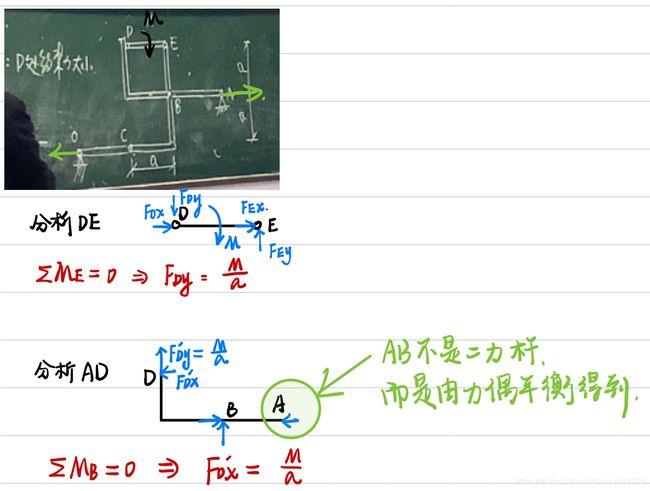
例三

1. 优先判断O处受力，根据"力偶只能用力偶来平衡"，确定A处受力
2. 分析DE，列∑M_E=0，得到F_Dy
3. 分析ABD，列∑M_B=0,得到F_Dx

例四

【区分】结点法是求内力的间接方法，截面法是求内力的直接方法

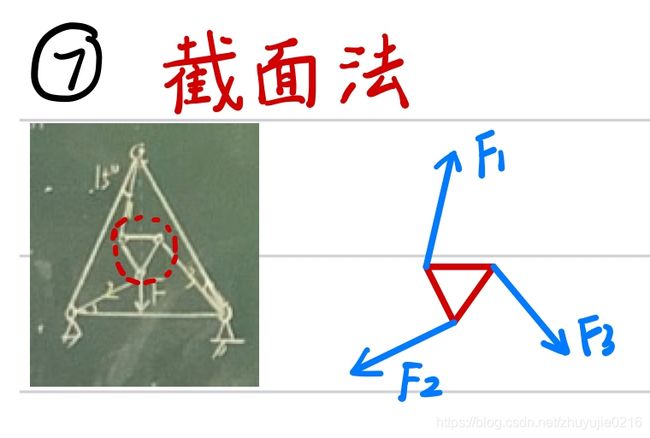
例五

1. A处是固定端，AC不是二力杆，结点法和截面法慎用！！！
2. 分析B结点，求出F₁和F₂
3. 取截面mm，列合适的矩平衡方程，求出F₃
4. 最后分析整体，三个独立方程，求解三个未知数

例六

取的截面不一定是直的，也可以是弯的，甚至可以是一个圆

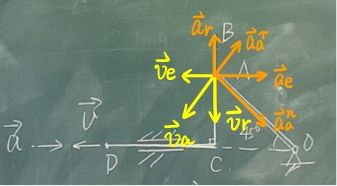
3. 为了某计算目标，指出动点，动系画速度合成图，加速度合成图（无科氏加速度）

注意点：

1. 千万不要去计算！！！
2. 用不同颜色的笔去画速度和加速度合成图
3. 根据速度来判断加速度，直线运动的加速度只有一个，圆周运动一定有向心加速度，有角加速度的还有切向加速度

例一

例二

此题比较简单，注意牵连速度**v_e**的方向是垂直于OC，因为牵连速度一定得要垂直于定点到动点的连线

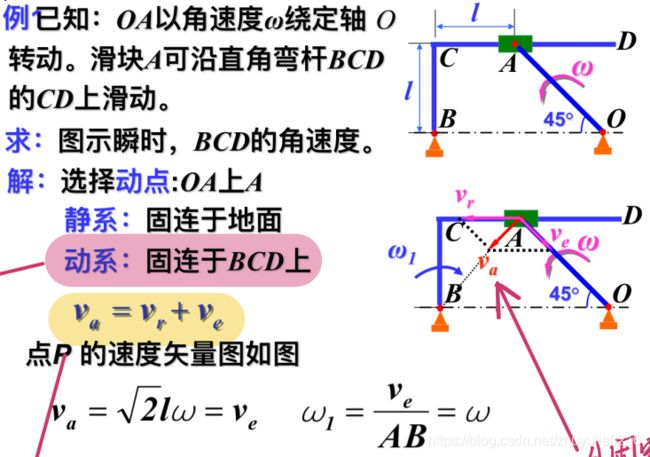
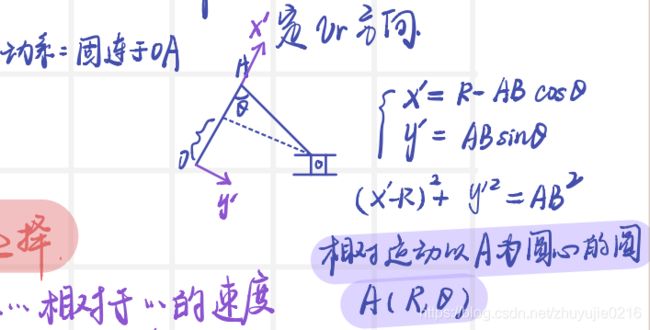
例三

A相当于CD的运动是：直线运动，相对运动比较明显，所以动点选择OA上的A点，动系选择BCD
注意此题的牵连速度垂直于BA，且与ω1的方向一致

例四

把圆心作为动点总是可以
动系做平移运动，故牵连速度就是动系的速度
因为BC之间的距离不变，所以相对运动实际上是以B为圆心的圆周运动

例五

显然，AM上的M点为动点，动系固连于AB杆（因为OC杆是、固定的，就把OC杆当做静系）

例六

例七

AB做平移运动，所以C点实际静止
不能形成平行四边形，只能用投影法

例八

这里动点只能选择圆心

例九

1. 相对运动的判断：将动系固连于OA，写出B点坐标（x’,y’）,得到相对运动的轨迹方程，从而判断相对速度的方向
2. 也可以用瞬时平移的知识，得到v_A=v_B

例十

例十一

例十二

动点是C，动系固连于AB上
注意相对速度的方向（AC距离不变）

4. 平面运动角速度，角加速度等计算

注意点：

1. 无质量，一定不是用动量定理、动量矩计算
2. 可以用瞬心法计算角速度，但是角加速度只能用基点法

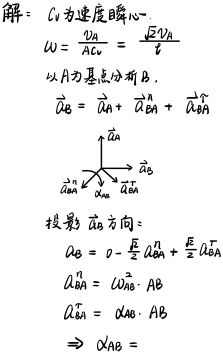
例一

为了避免涉及a_A，将加速度矢量表达式，投影到a_B方向

例二

1. 杆BC做平面运动
2. 利用瞬心法以及速度投影定理 ，速度必须在同一个物体上，所以动点选择BC上D点的影子D’

例四

例五

例六

圆轮又滚又滑，接触点不再是速度瞬心

例七

找速度瞬心一定要该物体上的速度

例八

5. 动力学普遍定理的应用

都可以用动静法计算

6. 动静法计算（以不变应万变，越复杂，优势越明显）

当计算角加速度时，方法有好到差依次是：转动方程→动静法→动能定理

例一

法一：找到加速度瞬心，用转动方程（M=Jα）
法二：动静法，补充两个惯性力和一个惯性力矩再列平衡方程（这里是对A点取矩）

例二

平移物体只需要考虑惯性力

例三

定轴转动的物体惯性力系的简化，既要加惯性力F_I，还要加惯性力矩M_I

例四

1. 本题是多个物体的动力学问题，所以要用整体和部分
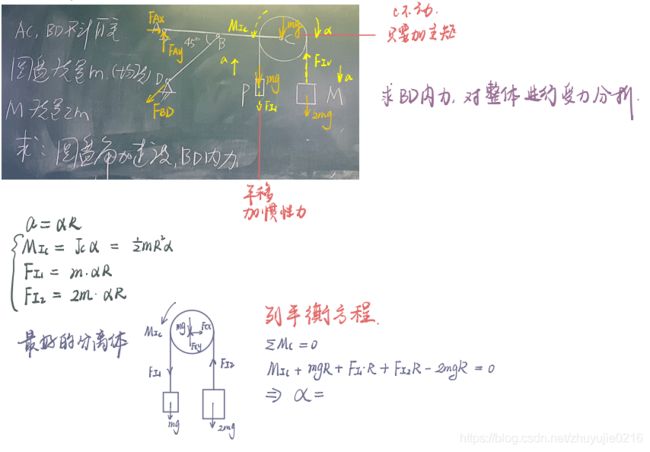
2. 选取圆盘和两个重物作为分析对象，需要加两个惯性力，一个惯性力矩，为了避免C处约束力，对C点取矩
3. 求BD内力，要么分析AC，但是Ａ处、Ｃ处约束力未知，最好的方法是对整体进行受力分析

例五

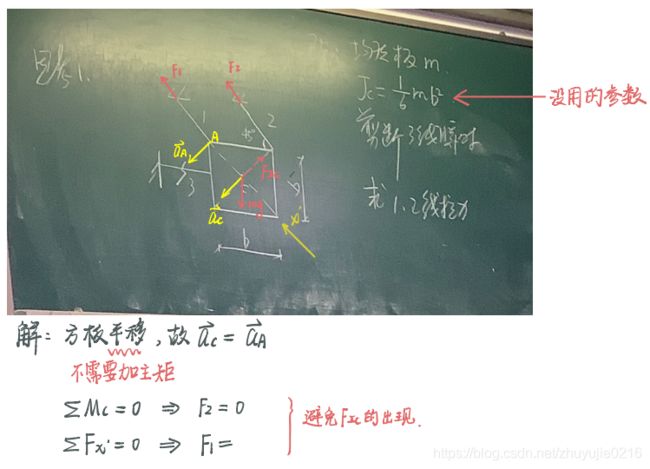
注意：方板平移，所以不需要加惯性力矩
三个独立方程，有四个未知数，但是还是可以求出F₁和F₂（选择合适的矩心和x’轴）

例六

总结：惯性力系不能向任一点简化的意思是“并不是向任一点简化，惯性力矩都是M_I该点=J_该点α”，只有质心/定点可以这么使用

例七

1. 圆盘做平移运动，不转；杆做定轴转动
2. 三个未知数，一定能求解
3. 注意求解顺序，先解出α，再解出F_Ax和F_Ay

例八

1. 足够粗糙的意思：纯滚动，所以摩擦系数f是无用的条件
2. 本题比较复杂，所以用动静法优势明显
3. 滚轮C和物体A的加速度都是a，所以两个轮的角加速度都是α
4. 先用整体法，解出α
5. 再分析滚轮C，解出F_IC

例九

1. 本题先找加速度瞬心，但是找不到
2. 先进行运动分析，OA定轴转动，AB平面运动，（C相对于A的运动是：绕A点的定轴转动）
3. 要知道C点的速度，自然想到以A为基点，分析C点

例十

加速度瞬心和动静法的比较：
最佳方法：1. 加速度瞬心+∑M_Ca 2. 加速度瞬心+动静法

例十一

1. C绕O点做定轴转动，有向心加速度、切向加速度，所以要加两个惯性力，一个惯性力矩
2. 对于环，只需要加一个惯性力矩
3. 明确有三个未知数：F_Ox、F_Oy、α，为了避免F_Ox、F_Oy，对O点取矩求出α
4. 再分析AB，可以计算出A处的焊接内力