python tensorflow学习(三)实战!lenet-5+mnist数据集
实战!lenet-5+mnist数据集
这两天真的超忙啊,一转眼三天没更了,满满的罪恶感+ing。
废话不多说,从这篇开始进入实战篇,接下来将使用tensorflow对卷积神经网络历史上最为经典的模型从lenet-5一直到ResNet进行实现。
大纲:
- MNIST数据集
- Lenet-5网络模型
MNIST数据集
对于卷积神经网络,MNIST手写体的识别就是入门的“hello world”,是最为简单的一个图片数据集。
MNIST数据集是一个手写数字数据库,他有60000个训练样本集和10000个测试样本集,下载地址为:http://yann.lecun.com/exdb/mnist/
下载之后包括4个文件:

从上往下依次为测试图像、测试标签、训练图像、训练标签
,对于MNIST数据集,tensorflow中有已经封装好的函数来读取该数据集。
from tensorflow.examples.tutorials.mnist import input_data
mnist_data_set = input_data.read_data_sets('MNIST_data', one_hot=True)
MNIST数据集图片的像素为28×28,为单通道。标签为1-10,对应0-9十个数字。
Lenet-5网络模型
1989年,LeCun提出第一个真正意义上的卷积神经网络,经过后来的改良,该模型能被应用于识别手写体字符等其他应用,LeCun提出了权值共享(weight sharing)和特征图(feature map)的概念并被流传至今,成为了卷积模块的基础。LeNet-5是其提出的第三种卷积神经网络模型,其模型结构如下:
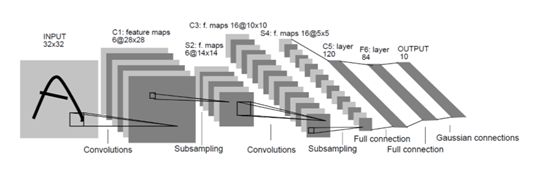
整个网络模型分为2个卷积模块、2个池化模块、2个全连接模块,最后再连接一个softmax模块,输出层为10个节点,分别代表1到9共10个数字。
首先定义占位符:
# 定义占位符
x = tf.placeholder('float32', [None, 784])
y = tf.placeholder('float32', [None, 10])
把输入向量变为28×28的矩阵形式:
# 把数据转换为矩阵形式
x_image = tf.reshape(x, [-1, 28, 28, 1])
对于卷积核和偏置量的初始化,为了减少代码冗余,我们在这里写一个初始化的函数
# 初始化卷积核
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
# 初始化偏置量
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
虽然tensorflow中有直接运算卷积核池化的方法,但是为了增强代码的可读性,我们把卷积和池化也抽象化为函数
# 抽象化卷积函数
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
# 抽象化池化函数
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
接下来开始一层一层的推导,第一层卷积核大小为5×5×6,卷积完之后应用relu激活函数,最后进行maxpooling
# 第一层卷积
W_conv1 = weight_variable([5, 5, 1, 6])
b_conv1 = bias_variable([6])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1)+b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
第二层卷积与第一层基本无异,只是通道数变为了16个:
W_conv2 = weight_variable([5, 5, 6, 16])
b_conv2 = bias_variable([16])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2)+b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
这样,经过两次卷积池化之后,图像的大小为7×7×16,为了进行接下来的全连接层,把图像展开为向量:
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])
然后进行两次全连接
# 第一层全连接
W_fc1 = weight_variable([7*7*16, 120])
b_fc1 = bias_variable([120])
h_fc1 = tf.nn.relu(tf.add(tf.matmul(h_pool2_flat, W_fc1), b_fc1))
# 第二层全连接
W_fc2 = weight_variable([120, 10])
b_fc2 = bias_variable([10])
h_fc2 = tf.nn.softmax(tf.add(tf.matmul(h_fc1, W_fc2), b_fc2))
采用交叉熵作为损失函数,使用Adam优化算法调整参数,定义正确率以便观察。
# 代价函数
cross_ntropy = -tf.reduce_sum(y*tf.log(h_fc2))
# 使用Adam优化算法调整参数
train_step = tf.train.GradientDescentOptimizer(1e-4).minimize(cross_ntropy)
# 正确率
correct_prediction = tf.equal(tf.arg_max(h_fc2, 1), tf.arg_max(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float32"))
初始化所有变量
# 初始化变量
sess.run(tf.initialize_all_variables())
设置一个列表存储精度的变化
c = []
开始训练
# 训练
for i in range(1000):
# 获取训练数据
batch_xs, batch_ys = mnist_data_set.train.next_batch(200)
if i % 2 == 0:
train_accuracy = accuracy.eval(feed_dict={
x: batch_xs, y: batch_ys})
c.append(train_accuracy)
print("step %d, train accuracy %g" % (i, train_accuracy))
# 训练数据
train_step.run(feed_dict={
x: batch_xs, y: batch_ys})
sess.close()
plt.plot(c)
plt.tight_layout()
plt.savefig('cnn-tf-mnist.png', dpi=200)
结果:
step 992, train accuracy 0.945
step 994, train accuracy 0.935
step 996, train accuracy 0.94
step 998, train accuracy 0.93
Process finished with exit code 0
 至此Lenet-5网络模型+MNIST数据集实现完成。
至此Lenet-5网络模型+MNIST数据集实现完成。
注:下一篇开始篇幅会比较长,内容较多,而且不会涉及神经网络理论的阐述。
啊终于写完惹,早点睡明天又要上课。。。本以为很闲的暑假突然就变得忙碌了,争取在这个月底前把这个系列更完。
如果效果不错的话,下个月再开一个系列,大概率更一个面向对象编程吧,毕竟听导师说科班出身应该对这些理解比较透彻。。。总之,这个暑假闲下来是不可能了QAQ