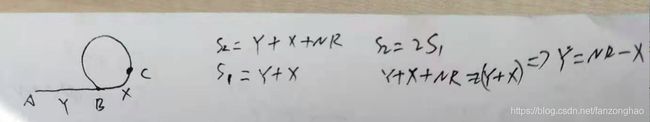python刷题+leetcode(第二部分)
一百零二.重复的子字符串
思路:
解法1.直接用python find方法
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
return (s+s).find(s,1)!=len(s)解法2.kmp算法
构造s+s作为主字符串,s作为模板字符串,再利用kmp即可。
一百零三.十进制整数的反码
class Solution:
def bitwiseComplement(self, N: int) -> int:
# res = []
# for bin_i in bin(N)[2:]:
# if int(bin_i):
# res.append('0')
# else:
# res.append('1')
# print(res)
# print('0b'+''.join(res))
# return int('0b'+''.join(res),2)
return int('0b'+''.join('0' if int(bin_i) and 1 else '1' for bin_i in bin(N)[2:]), 2)
一百零三.最小移动次数使数组元素相等
思路:让n-1个元素加1等于让一个元素-1
代码:
class Solution:
def minMoves(self, nums: List[int]) -> int:
moves = 0
nums = sorted(nums)
for i in range(len(nums)):
moves+=nums[i]-nums[0]
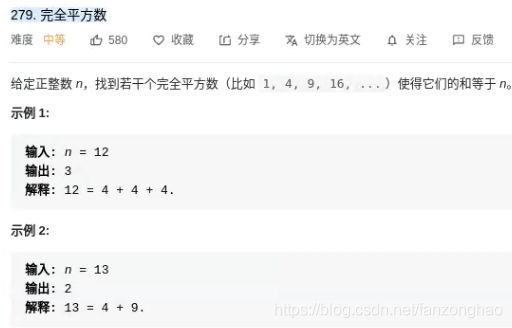
return moves一百零四. 完全平方数
思路:可看成M(n) = M(n-1k)+1,这里就可以用回溯当成求子集问题
1.回溯
#公式为 M(n) = M(n - k) + 1
import math
class Solution(object):
def numSquares(self, n):
square_nums = [i**2 for i in range(1, int(math.sqrt(n))+1)]
print('==square_nums:', square_nums)
res = []
track = []
def minNumSquares(k,track):
""" recursive solution """
# bottom cases: find a square number
if k in square_nums:
track.append(k)
res.append(track)#满足选择条件
return 1
min_num = float('inf')
# Find the minimal value among all possible solutions
for square in square_nums:
if k < square:
break
# 满足选择列表
store = track.copy()
track.append(square)#做选择
new_num = minNumSquares(k-square, track) + 1#回溯
track = store#撤消选择
min_num = min(min_num, new_num)
return min_num
return minNumSquares(n, track), res
n = 3
sol = Solution()
numbers, res = sol.numSquares(n)
print('个数:', numbers, res)
2.对于递归这种,其实都是可以用dp来减少计算量
#公式为 M(n) = M(n - k) + 1
class Solution(object):
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
square_nums = [i ** 2 for i in range(0, int(math.sqrt(n)) + 1)]
print('square_nums==:', square_nums)
dp = [float('inf')] * (n + 1)
# bottom case
dp[0] = 0
for i in range(1, n + 1):
for square in square_nums:
if i < square:#小于平方的数 就break
break
print('==square:', square)
dp[i] = min(dp[i], dp[i - square] + 1)
print('==dp:', dp)
return dp[-1]
n = 4
sol = Solution()
numbers = sol.numSquares(n)
print('个数:', numbers)一百零五.阶乘后的零
思路:找尾数是0也就是除于10,10可以拆成5*2,通过找规律可以知道出现2的次数比5多,也就变成了找5的个数
class Solution:
def trailingZeroes(self, n: int) -> int:
res= 0
while n>0:
n = n//5
res +=n
return res一百零六. 整数拆分
思路:j是 拆分的第一个数字,i-j就是剩下的,求i的最大等价于求i-j的最大,故状态转移方程为:max(j*(i-j),j*dp[i-j])
1.dp解法
#dp[i] = max(j*(i-j),j*dp[i-j])
class Solution:
def integerBreak(self, n):
dp = [0 for i in range(n+1)]
# print('==dp:', dp)
for i in range(n+1):#
value = 0
for j in range(i):#循环去确定i的时候的最大值
value = max(value, max(j*(i-j), j*dp[i-j]))
dp[i] = value
# print('==dp:', dp)
return dp[-1]
sol = Solution()
res = sol.integerBreak(n=10)
print('res:', res)2.递归解法
class Solution:
def integerBreak(self, n):
if n<=1:
return 0
if n == 2:
return 1
res = 0
for i in range(2, n):
res = max(res, max(i*(n-i), i*self.integerBreak(n-i)))
return res
sol = Solution()
res = sol.integerBreak(n=35)
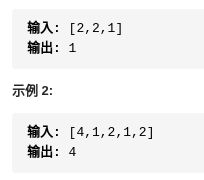
print('res:', res)一百零七,只出现一次的数字 1,给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
思路:利用异或,相同为0,不同为1
#方法1
a=[4,1,2,2,1]
b=set(a)
print(b)
print(2*sum(b)-sum(a))
#方法2:
a=[4,1,1]
res=0
for i in a:
res^=i
print('res=',res)
#方法3:
a=[4,1,2,1,2]
from functools import reduce
b=reduce(lambda x,y:x^y,a)
print('b=',b)一百零八.只出现一次的数字 II ,给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
思路:0与任何数异或为该数,两个相同的数异或为0,需要两个位运算符来存储单次和三次出现的值
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# return (3 * sum(set(nums)) - sum(nums)) // 2
seen_once = seen_twice = 0
for num in nums:
seen_once = ~seen_twice & (seen_once ^ num)
seen_twice = ~seen_once & (seen_twice ^ num)
return seen_once一百零九.错误的集合
解法一:数学解法
class Solution:
def findErrorNums(self, nums: List[int]) -> List[int]:
count = sum(set(nums))
return [sum(nums)-count, len(nums)*(len(nums)+1)//2 - count]解法二:位运算
def findErrorNums(nums):
res = 0
length = len(nums)
err = sum(nums) - sum(set(nums)) # 重复
print('err:', err)
for n in nums:#求出非重复数之和
res ^= n
print('res:', res)
for i in range(1, length + 1):#求出重复数之前的值
res ^= i
print('==res:', res)
miss = err ^ res#求出缺失值
print('===miss:', miss)
return [err, miss]
nums = [1, 2, 2, 4]
findErrorNums(nums)一百一十:连续数列
思路:动态规划,找到状态方程dp[i]=max(nums[i]+dp[i-1], nums[i])
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0 for i in range(len(nums))]
# print('===dp', dp)
dp[0] =nums[0]
for i in range(1, len(nums)):
dp[i] = max(nums[i], dp[i-1]+nums[i])
# print('==dp:', dp)
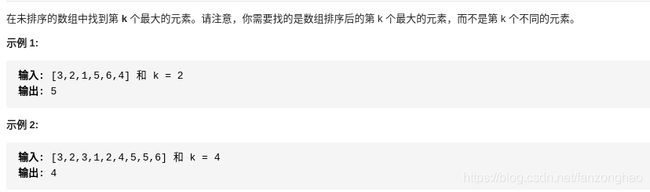
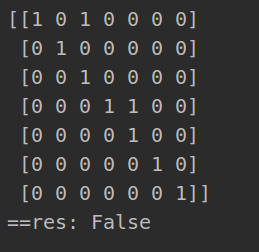
return max(dp)一百一十一:编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
思路:找到值最大的一行的左下角,如果值小就减少行,值大就增加列.
class Solution:
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if len(matrix)<=0:
return False
if len(matrix[0])<=0:
return False
h = len(matrix)
w = len(matrix[0])
col, row = 0, h - 1
#先找到最大值的一行 左下脚
while row >= 0 and col < w:
if target>matrix[row][col]:
col+=1
elif target < matrix[row][col]:
row-=1
else:
return True
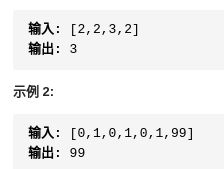
return False一百一十二.最小K个数
思路:排序 取前几个k值即可.
class Solution:
def smallestK(self, arr: List[int], k: int) -> List[int]:
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
return quicksort(arr)[:k]一百一十三.数组中的第K个最大元素
思路:排序 取第k个值就可
class Solution:
def quicksort(self, arr):
if len(arr) <= 1:
return arr
privot = arr[len(arr) // 2]
left = [i for i in arr if i < privot]
middle = [i for i in arr if i == privot]
right = [i for i in arr if i > privot]
# left = [arr[i] for i in range(len(arr)) if arr[i] < privot]
# middle = [arr[i] for i in range(len(arr)) if arr[i] == privot]
# right = [arr[i] for i in range(len(arr)) if arr[i] > privot]
return self.quicksort(left) + middle + self.quicksort(right)
def findKthLargest(self, nums, k):
return self.quicksort(nums)[::-1][k-1]
# nums = [3, 2, 1, 5, 6, 4]
# k = 2
nums = [3,2,3,1,2,4,5,5,6]
k = 4
sol = Solution()
res = sol.findKthLargest(nums, k)
print('res:', res)一百一十四.加油站
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
nums_of_station = len(gas)
total_ = 0
curent_= 0
st_station = 0
for i in range (nums_of_station):
total_ +=gas[i] - cost[i]
curent_ +=gas[i] - cost[i]
if curent_<0:
st_station=i+1
curent_=0
return st_station if total_>=0 else -1一百一十五.根据身高重建队列
思路:按身高由高到低进行排序,身高相等时按索引从小排序
#新建一个队列按照索引进行插入
![]()
#思路:按身高由高到低进行排序,身高相等时按索引从小排序
#新建一个队列按照索引进行插入
class Solution:
def reconstructQueue(self, people):
people = sorted(people, key=lambda x: (-x[0], x[1]))
print('===people:', people)
output = []
for p in people:
print('===p:', p)
output.insert(p[1], p)
print('==output:', output)
return output
people = [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
sol = Solution()
sol.reconstructQueue(people)116.避免重复字母的最小删除成本
思路:找到相邻的字母,对其相应的损失取最小相加,注意的是碰到小的值要进行交换,否则会拿小的值再次计算和.
class Solution:
def minCost(self, s, cost):
price = 0
for i in range(len(s)-1):
if s[i] == s[i+1]:
price += min(cost[i], cost[i+1])
if cost[i] > cost[i+1]:#碰到小的值进行交换 不交换的话会拿小的值再一次进行相加
cost[i], cost[i+1] = cost[i+1], cost[i]
# print('==price', price)
return price
# s = "abaac"
# cost = [1, 2, 3, 4, 5]
s = "aaabbbabbbb"
cost = [3, 5, 10, 7, 5, 3, 5, 5, 4, 8, 1]
# s = "aabaa"
# cost = [1, 2, 3, 4, 1]
sol = Solution()
price = sol.minCost(s, cost)
print('=price:', price)117.合并有序数组
思路:两个指针分别指向两个列表,进行值的比较,将小的值放进列表,最后在看指针有没有走完
class Solution(object):
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: None Do not return anything, modify nums1 in-place instead.
"""
nums1_copy = nums1[:m]
nums1[:] = []
# 双指针法
p1 = 0
p2 = 0
#将小的值放进res
while p1 < m and p2 < n:
if nums1_copy[p1] < nums2[p2]:
nums1.append(nums1_copy[p1])
p1 += 1
else:
nums1.append(nums2[p2])
p2 += 1
# 在把剩下的元素进行添加
if p1 < m:
nums1[p1 + p2:] = nums1_copy[p1:]
if p2 < n:
nums1[p1 + p2:] = nums2[p2:]
return nums1118-1. 课程表
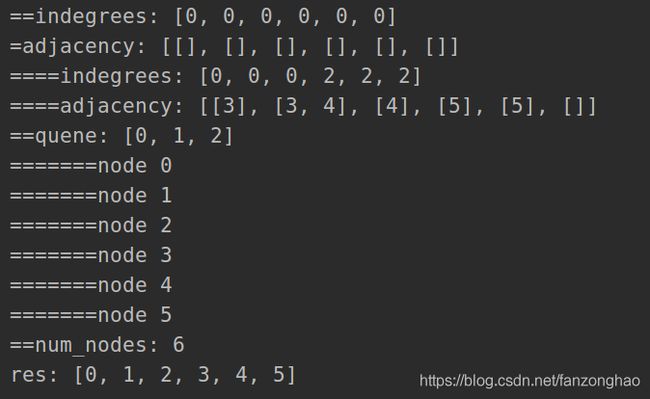
思路:对于这种从图找拓扑排序 ,只有有向无环图能够找到,将入度为0的节点先进入队列,在利用bfs进行出队处理,此时将出队的节点的下一个节点的度进行减一计数,同时遍历的节点数进行加一,最终节点都进行了遍历,则说明找到了拓扑排序.
思路1:用邻接列表
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 入度列表
print('==indegrees:', indegrees)
adjacency = [[] for i in range(numCourses)] # 邻接列表 存储节点的下一个节点
print('=adjacency:', adjacency)
#得到入度和每个课程的邻接列表
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur)
print('====indegrees:', indegrees)
print('====adjacency:', adjacency)
quene = []
# 如果度为0 就进入队列
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
while quene:
node = quene.pop(0)
num_nodes += 1
for next_node in adjacency[node]:
indegrees[next_node] -= 1 # 找出下一个点相应的度-1
if indegrees[next_node] == 0: # 入度为0
quene.append(next_node)
print('==num_nodes:', num_nodes)
return num_nodes == numCourses
# numCourses, prerequisites = 2, [[1, 0]]
# numCourses, prerequisites = 2, [[1, 0], [0, 1]]
numCourses, prerequisites = 6, [[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
sol = Solution()
res = sol.canFinish(numCourses, prerequisites)
print('res:', res)思路2:用邻接矩阵的bfs
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 度列表
adjacency = [[0 for i in range(numCourses)] for i in range(numCourses)] # 邻接矩阵 表示节点之间关系
print('==init adjacency:', adjacency)
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre][cur] = 1
print('==init adjacency complete:', adjacency)
print('==init indegrees complete:', indegrees)
quene = []
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
while quene:
node = quene.pop()
num_nodes += 1
for j in range(numCourses):
if adjacency[node][j] == 1:
next_node = j
adjacency[node][j] -= 1
indegrees[next_node] -= 1
if indegrees[next_node] == 0:
quene.append(next_node)
print('==num_nodes:', num_nodes)
return num_nodes == numCourses
# numCourses = 2
# prerequisites = [[0, 1]]
numCourses = 4
prerequisites = [[1, 0], [2, 0], [3,1],[3,2]]
sol = Solution()
sol.canFinish(numCourses, prerequisites)118-2:课程表 II
思路:有向无环图,BFS遍历
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 入度列表
print('==indegrees:', indegrees)
adjacency = [[] for i in range(numCourses)] # 邻接列表
print('=adjacency:', adjacency)
#得到入度和每个课程的邻接列表
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur)
print('====indegrees:', indegrees)
print('====adjacency:', adjacency)
quene = []
# 如果度为0 就进入队列
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
learn_node = []
while quene:
node = quene.pop(0)
print('=======node', node)
learn_node.append(node)
num_nodes += 1
for next_node in adjacency[node]:
indegrees[next_node] -= 1 # 找出下一个点相应的度-1
if indegrees[next_node] == 0: # 入度为0
quene.append(next_node)
print('==num_nodes:', num_nodes)
return learn_node if num_nodes == numCourses else []
# numCourses, prerequisites = 2, [[1, 0]]
# numCourses, prerequisites = 2, [[1, 0], [0, 1]]
numCourses, prerequisites = 6, [[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
sol = Solution()
res = sol.canFinish(numCourses, prerequisites)
print('res:', res)思路2:用邻接矩阵的bfs
class Solution:
def canFinish(self, numCourses, prerequisites):
indegrees = [0] * numCourses # 度列表
adjacency = [[0 for i in range(numCourses)] for i in range(numCourses)] # 邻接矩阵 表示节点之间关系
print('==init adjacency:', adjacency)
for cur, pre in prerequisites:
indegrees[cur] += 1
adjacency[pre][cur] = 1
print('==init adjacency complete:', adjacency)
print('==init indegrees complete:', indegrees)
quene = []
for i in range(len(indegrees)):
if indegrees[i] == 0:
quene.append(i)
print('==quene:', quene)
num_nodes = 0
learn_nodes = []
while quene:
node = quene.pop()
learn_nodes.append(node)
num_nodes += 1
for j in range(numCourses):
if adjacency[node][j] == 1:
next_node = j
adjacency[node][j] -= 1
indegrees[next_node] -= 1
if indegrees[next_node] == 0:
quene.append(next_node)
print('==num_nodes:', num_nodes)
print('=learn_nodes:', learn_nodes)
return learn_nodes if num_nodes == numCourses else []
# numCourses = 2
# prerequisites = [[0, 1]]
numCourses = 4
prerequisites = [[1, 0], [2, 0], [3,1],[3,2]]
sol = Solution()
sol.canFinish(numCourses, prerequisites)
119. 上升下降字符串
思路:利用桶计数对每个字符建立桶,进行左右扫描直到都为空
方法1:
class Solution:
def sortString(self, s):
#构建每个字符的桶 用于计数
barrel = [0]*26
for i in s:
barrel[ord(i)-97] += 1
# print('==barrel:', barrel)
res = []
while True:
if any([barrel[i] for i in range(26)]):#退出条件 如果所有桶的字符都为0
for i in range(len(barrel)):#从小到大加字符
if barrel[i]>0:
barrel[i]-=1
res.append(chr(i+97))
# print('res:', res)
# print('==barrel:', barrel)
for i in range(len(barrel)-1, -1, -1):#从大到小加字符
if barrel[i]>0:
barrel[i]-=1
res.append(chr(i+97))
else:
break
# print('res:', res)
return ''.join(res)
sol = Solution()
s = "aaaabbbbcccc"
res = sol.sortString(s)
print('res:', res)方法2:利用collections
import collections
class Solution:
def sortString(self, s):
chars=collections.Counter(s)
print(chars)
ans=[]
signal=0
while chars:
group=list(chars)
print('==group:', group)
group.sort(reverse=signal)
print('====group:', group)
ans.extend(group)
print('====collections.Counter(group):',collections.Counter(group))
chars-=collections.Counter(group)
print('===chars:', chars)
signal=1-signal
return ''.join(ans)
sol = Solution()
s = "aaaabbbbcccc"
res = sol.sortString(s)120.字符串压缩
思路:从左到右遍历字符串,开出两个变量,一个用于计数,一个用于更新字符
class Solution(object):
def compressString(self, S):
"""
:type S: str
:rtype: str
"""
if len(S)==0:
return ''
S_start = S[0]#将字符串中的第一个字符作为开始字符串
cnt = 0
res = ''
for i in range(len(S)):
if S[i] == S_start: # 等于开始字符就进行计数
cnt += 1
else:
res += S_start + str(cnt)#碰到不等于的字符 将字符开头和出现次数加入结果集合
S_start = S[i]#重新更新开始字符串
cnt = 1#重新计数
# print('res:', res)
res += S_start + str(cnt)
# print('res:', res)
return S if len(res) >= len(S) else res121.破坏回文串
思路: 1. 回文字符串特点 奇数 偶数都只找一半即可
2. 对于前半部分如果发现不为a的替换成a即可 否则说明前半部分都是a这个时候就将后半部分变为b即可
class Solution(object):
def breakPalindrome(self, palindrome):
"""
:type palindrome: str
:rtype: str
"""
if len(palindrome) <= 1:
return ''
# 回文字符串特点 奇数 偶数都只找一半即可
# 对于前半部分如果发现不为a的替换成a即可 否则说明前半部分都是a这个时候就将后半部分变为b即可
for i in range(len(palindrome) // 2):
if palindrome[i] != 'a':
return palindrome[:i]+'a'+palindrome[i+1:]
return palindrome[:-1]+'b'122.恢复空格
#思路:通过双指针来遍历找到是否在dictionary,开辟一个列表用于计数未识别的字符数
# 利用字典key的特性方便进行判断
class Solution(object):
def respace(self, dictionary, sentence):
#思路:通过双指针来遍历找到是否在dictionary,开辟一个列表用于计数未识别的字符数
# 利用字典key的特性方便进行判断
dict_ = {}
for dictionary_str in dictionary:
dict_[dictionary_str] = ''
print('===dict_:', dict_)
opt = (len(sentence)+1) * [0]
print('==opt:', opt)
for i in range(1, len(sentence)+1):#加1 是因为要走到最后来判断是否在字典里面
opt[i] = opt[i - 1] + 1
for j in range(i):
if sentence[j:i] in dict_:
opt[i] = min(opt[i], opt[j])
print('==opt:', opt)
return opt[-1]
sol = Solution()
# dictionary = ["haha", "look"]
# sentence = "hahhahalookme"
# dictionary = ["h"]
# sentence = "aaa"
dictionary = ["looked", "just", "like", "her", "brother"]
sentence = "jesslookedjustliketimherbrother"
sol.respace(dictionary, sentence)125.连续差相同的数字
思路:第一位数字有9种可能性,后面的数字分别有两种可能性,故对于一个5位数字,有9*2^4种可能性,故直接遍历即可
class Solution(object):
def numsSameConsecDiff(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[int]
"""
"""
:type n: int
:type k: int
:rtype: List[int]
"""
if n == 1:
return [0]
res = [i for i in range(1, 10)]
for i in range(n - 1):
temp = []
for j in res:
d = j % 10
if d - k >= 0:
temp.append(10 * j + d - k)
if d + k <= 9:
temp.append(10 * j + d + k)
print('==temp:', temp)
res = temp
return list(set(res))
N = 3
K = 2
sol = Solution()
sol.numsSameConsecDiff(N, K)126.水域大小
思路1:bfs 将为0的坐标存入队列,在对上下左右斜等8个方向用bfs进行遍历,需要注意的是遍历过为0的点需要更新为-1,代表已经遍历过了,否则会陷入无限循环
class Solution(object):
def pondSizes(self, land):
"""
:type land: List[List[int]]
:rtype: List[int]
"""
res = []
rows = len(land)
columns = len(land[0])
for i in range(rows):
for j in range(columns):
if land[i][j] == 0: # 找到水域
land[i][j] = -1 # 将访问的点标记进行标记
quene = []
quene.append([i, j])
temp_water_num = 1
while len(quene) > 0:
x, y = quene.pop(0)
directions = [[x, y - 1], [x, y + 1], [x - 1, y - 1], [x - 1, y],
[x - 1, y + 1], [x + 1, y - 1], [x + 1, y], [x + 1, y + 1]]
for new_x, new_y in directions:
# print('==new_x, new_y :', new_x, new_y)
if 0 <= new_x < len(land) and 0 <= new_y < len(land[0]) and land[new_x][new_y] == 0:
temp_water_num += 1
quene.append([new_x, new_y])
land[new_x][new_y] = -1 # 将访问的点标记进行标记
res.append(temp_water_num)
print('==res:', res)
return sorted(res)
sol = Solution()
land = [[0, 2, 1, 0],
[0, 1, 0, 1],
[1, 1, 0, 1],
[0, 1, 0, 1]]
sol.pondSizes(land)思路2:递归 对经过的0进行更新替换 每掉一次递归 就用一个变量+1 记录水域的个数
class Solution:
def helper(self, i, j, h, w):
if i < 0 or i >= h or j < 0 or j >= w or self.land[i][j] != 0:
return
self.temp += 1
self.land[i][j] = -1
self.helper(i - 1, j, h, w)
self.helper(i + 1, j, h, w)
self.helper(i, j-1, h, w)
self.helper(i, j+1, h, w)
self.helper(i-1, j - 1, h, w)
self.helper(i-1, j + 1, h, w)
self.helper(i+1, j - 1, h, w)
self.helper(i+1, j + 1, h, w)
def pondSizes(self, land):
self.land = land
h = len(self.land)
w = len(self.land[0])
res = []
for i in range(h):
for j in range(w):
if self.land[i][j] == 0:
self.temp = 0
self.helper(i, j, h, w)
res.append(self.temp)
# print(res)
return sorted(res)
land = [
[0,2,1,0],
[0,1,0,1],
[1,1,0,1],
[0,1,0,1]
]
sol = Solution()
res = sol.pondSizes(land)
print('==res:', res)127.计算各个位数不同的数字个数
![]()
思路:n=0有一位, n=1有10位,n=2 有 9*9位 n=3有9*9*8 n=4有9*9*8*7 大于10位就固定了
class Solution(object):
def countNumbersWithUniqueDigits(self, n):
"""
:type n: int
:rtype: int
"""
# n=0有一位, n=1有10位,n=2 有 9*9位 n=3有9*9*8 n=4有9*9*8*7 大于10位就固定了
if n == 0:
return 1
temp = 9
k = 9
res = 10
for i in range(1, min(n, 10)):
temp *= k
res += temp
k -= 1
print('res:', res)
return res
sol = Solution()
n = 10
sol.countNumbersWithUniqueDigits(n)
128.最大整除子集
思路:一个子集中的最大数能够被整数 这个子集中的其他数就不需要在除了 故先对数字进行排序 依次找子集 最后返回最长的子集即可
class Solution(object):
def largestDivisibleSubset(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
if len(nums)==0:
return []
nums = sorted(nums)
opt = [[num] for num in nums]
for i in range(len(nums)):
for j in range(i-1, -1, -1):
if nums[i]%nums[j]==0:# 整数满足除于子集中的最大值余数为0 则将整数加入子集
if len(opt[j])+1>len(opt[i]):
opt[i] = opt[j]+[nums[i]]
# print('===opt:',opt)
return max(opt, key=len)
129.数值的整数次方
思路:对于偶数指数一分为2即可, 对于奇数指数一分为2 在乘以底数即可
#思路:对于偶数指数一分为2即可, 对于奇数指数一分为2 在乘以底数即可
class Solution(object):
def myPow(self, x, n):
"""
:type x: float
:type n: int
:rtype: float
"""
# 2^5= 2^2 * 2^2 *2
# 2^4= 2^2 * 2^2
def get_power(x, n):
# 递归终止条件
if n == 0:
return 1
if x == 1:
return 1
# print('===r:', r)
if n % 2 == 0: # 偶数的情况
# 二分法的一半
r = get_power(x, n / 2) # 分
return r * r # 合
else: # 奇数的情况
r = get_power(x, (n - 1) / 2) # 分
return r * r * x # 合
if n > 0:
res = get_power(x, n)#指数为正
else:
res = 1 / get_power(x, -n)#指数为负
return res
sol = Solution()
x = 2.00000
n = 2
res = sol.myPow(x, n)
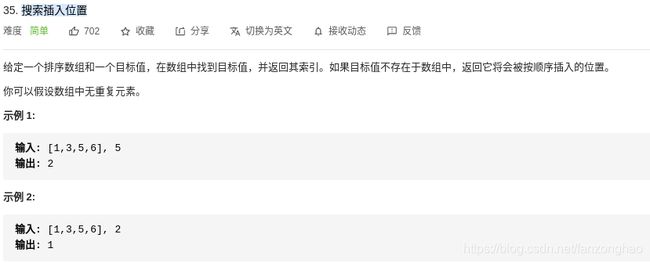
print('==res:', res)130-1.搜索插入位置
思路:二分查找 利用二分法不断逼近目标数的索引
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
#二分查找
left,right=0,len(nums)-1
while left<=right:
middle = left+(right-left)//2
if nums[middle]>=target:
right = middle-1
else:
left=middle+1
return left
130-2.在排序数组中查找元素的第一个和最后一个位置
思路1:双指针,时间复杂度O(n)
#O(n)
class Solution:
def searchRange(self, nums, target):
left,right = 0,len(nums)-1
while left < right:
if nums[left]==target and nums[right]==target:
return [left,right]
elif nums[left]思路2:二分查找法,时间复杂度O(logn)
重点是找到左边界和右边界
class Solution:
def serachLeft(self, nums, target):
left, right = 0, len(nums) - 1
while left <= right:
middle = left + (right - left) // 2
if nums[middle] < target:
left = middle+1
else:
right = middle-1
return left
def serachRight(self, nums, target):
left, right = 0, len(nums) - 1
while left <= right:
middle = left + (right - left) // 2
if nums[middle] <= target:#加个等于符号 这样left就可以找到最后一个
left = middle + 1
else:
right = middle - 1
return left-1
def searchRange(self, nums, target):
left = self.serachLeft(nums, target)
# print('==left:', left)
right = self.serachRight(nums, target)
# print('==right:', right)
if left<=right:
return [left,right]
else:
return [-1, -1]
# nums = [5, 7, 7, 8, 8, 8]
nums = [5, 7, 7, 9, 9, 9]
target = 8
sol = Solution()
sol.searchRange(nums, target)
130-3.搜索旋转排序数组
思路:判断中值和右值的关系来决定是否是有序的,通过缩短为有序数组 在进行二分法查找
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right=0,len(nums)-1
while left<=right:
middle = left + (right-left)//2
if nums[middle]==target:
return middle
if nums[middle]130-4.搜索旋转排序数组 II
思路:判断左右两个子序 注意需要去除 避免对顺序造成的干扰
class Solution:
def search(self, nums: List[int], target: int) -> bool:
left,right = 0,len(nums)-1
while left<=right:
middle = left+(right-left)//2
if nums[middle]==target:
return True
if (nums[middle] == nums[left] == nums[right]):#去除边界重复值
left += 1
right -= 1
elif nums[middle]>=nums[left]:#left到middle有序
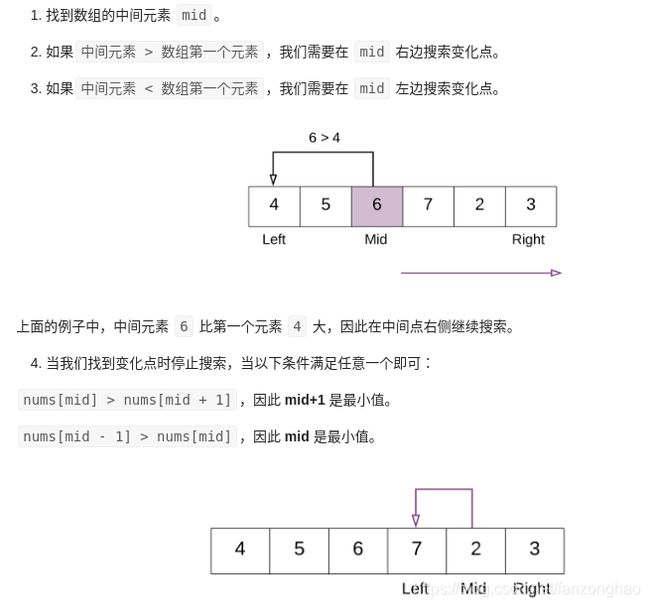
if nums[left]<=target130-5.寻找旋转排序数组中的最小值
思路:
class Solution:
def findMin(self, nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
left,right = 0,len(nums)-1
if nums[right]>nums[left]:
return nums[left]
while left<=right:
middle = left+(right-left)//2
if nums[middle]>nums[middle+1]:#找到突变点
return nums[middle+1]
if nums[middle-1]>nums[middle]:
return nums[middle]
if nums[middle]>nums[left]:
left=middle + 1
else:
right = right -1
131.第一个错误的版本
思路:其实就是查找第一个值,利用双指针,故左指针与右指针不会相遇,对于左指针更新采用middle+1,而右指针为middle即可.
# The isBadVersion API is already defined for you.
# @param version, an integer
# @return a bool
# def isBadVersion(version):
class Solution:
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
#二分查找
left,right = 1,n
while left132.二分查找
思路:双指针遍历即可
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right = 0,len(nums)-1
while left<=right:
middle = left + (right-left)//2
if nums[middle]==target:
return middle
elif nums[middle]133.最长上升子序列
思路:利用动态规划存储 上升序列的值
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if len(nums)==0:
return 0
dp = len(nums)*[0]
dp[0] = 1
for i in range(1, len(nums)):
value = 0
for j in range(i):
if nums[i]>nums[j]:
value = max(value, dp[j])
dp[i] = value+1
# print('==dp:',dp)
return max(dp)事先先把dp存储值为1
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if len(nums)==0:
return 0
dp = len(nums) * [1]
for i in range(1, len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+1)
# print('==dp:', dp)
return max(dp)138.单词规律
思路:
1. 当s中单词数和pattern长度不相同时,直接可以判断为不匹配
2. 当s中单词数和pattern长度相同时:
# 以pattern中的单词作为key,以str中的元素作为value。遍历pattern,s,
# 当pattern中的单词未出现过时,判断其是否在字典中的key值出现过:
# 若是,则判断其对应的value是否出现过,若冲突返回不匹配;
#若否,判断是否出现在字典中的value:若是,返回不匹配;若否,加入字典.
class Solution(object):
def wordPattern(self, pattern, s):
"""
:type pattern: str
:type str: str
:rtype: bool
"""
s = s.split(' ')
if len(pattern)!=len(s):#s的长度与pattern不一样就返回False
return False
dic_ = {}
for i, x in enumerate(s):
# print('==dic_:', dic_)
if pattern[i] not in dic_:
# print('==dic_.values():', dic_.values())
if x in dic_.values():
return False
dic_[pattern[i]] = x
else:
if x != dic_[pattern[i]]:
return False
return True
# pattern = "abba"
# s = "dog cat cat dog"
pattern = "abba"
s = "dog dog dog dog"
sol = Solution()
res = sol.wordPattern(pattern, s)
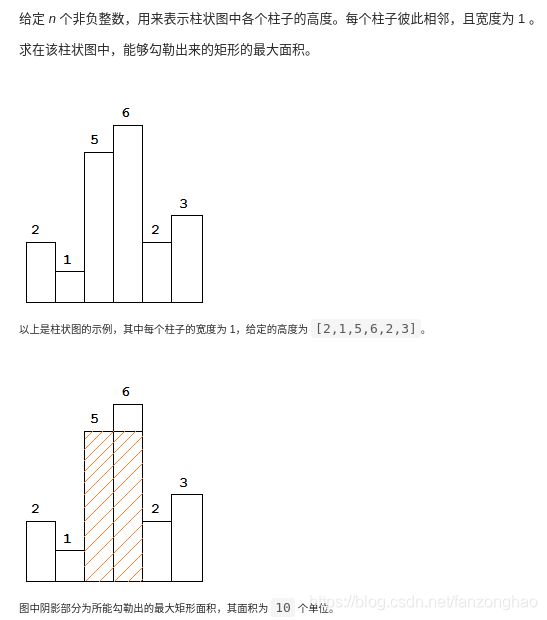
print('==res:', res)139.柱状图中最大的矩形
思路1:暴力枚举,直接向左右扩撒直到找到小于heights[i]的点
超时:
class Solution:
def largestRectangleArea(self, heights):
res = 0
for i in range(len(heights)):
# print('==i:', i)
left_i = i
right_i = i
# print(stack)
while left_i >= 0 and heights[left_i] >= heights[i]:
left_i-=1
while right_i= heights[i]:
right_i+=1
# print('==left_i,right_i:', left_i,right_i)
res = max(res, (right_i - left_i - 1)*heights[i])
return res
heights = [2,1,5,6,2,3]
# heights = [0,9]
# heights = [2,0,2]
# heights = [4,2,0,3,2,4,3,4]
sol = Solution()
sol.largestRectangleArea(heights) 思路2:单调递增栈
#单调递增栈 将依次增加的值放入栈中,出现小于栈的值则进行出栈计算面积
class Solution:
def largestRectangleArea(self, heights):
stack = []
heights = [0] + heights + [0]
res = 0
for i in range(len(heights)):
while stack and heights[stack[-1]] > heights[i]:
# print('heights', heights)
print('===i:', i)
print('==stack:', stack)
tmp = stack.pop()
print('==tmp:', tmp)
width = (i - stack[-1] - 1)
res = max(res, width * heights[tmp])
print('==res:', res)
stack.append(i)
return res
heights = [2,1,5,6,2,3]
# heights = [0,9]
# heights = [2,0,2]
# heights = [4,2,0,3,2,4,3,4]
sol = Solution()
sol.largestRectangleArea(heights)
144.三角形的最大周长
思路:两边之和大于第三边,可以从小到大排序,尽可能选最长边.
class Solution:
def largestPerimeter(self, A: List[int]) -> int:
A =sorted(A)
#三角形满足两边之和大于第三边
for i in range(len(A)-3, -1, -1):
if A[i]+A[i+1]>A[i+2]:
return A[i]+A[i+1]+A[i+2]
return 0
149.连续子数组的最大和
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
opt = [0]*len(nums)
opt[0] = nums[0]
for i in range(1,len(nums)):
opt[i] = max(opt[i-1]+nums[i],nums[i])
return max(opt)150-1. 乘积最大子数组
![]()
思路1:找到状态转移方程:
maxf[i]:表示在i处最大连乘数
minf[i]:表示在i处最小连乘数
maxf[i] = max(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
minf[i] = min(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
#maxf[i]:表示在i处最大连乘数
#minf[i]:表示在i处最小连乘数
#maxf[i] = max(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
#minf[i] = min(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1])
class Solution:
def maxProduct(self, nums):
n = len(nums)
maxf,minf = [0]*n,[0] * n
maxf[0],minf[0] = nums[0],nums[0]
for i in range(1,n):
maxf[i] = max(nums[i], nums[i] * minf[i - 1], nums[i] * maxf[i-1])
minf[i] = min(nums[i], nums[i] * minf[i - 1], nums[i] * maxf[i-1])
print('==maxf:', maxf)
return max(maxf)
nums = [2,3,-2,4]
sol = Solution()
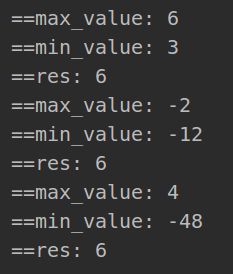
sol.maxProduct(nums)思路2:优化版 由于第 i 个状态只和第 i - 1个状态相关,可以只用两个变量来维护 i - 1时刻的状态,一个维护 max, 一个维护 min
class Solution:
def maxProduct(self, nums):
min_value = nums[0]
max_value = nums[0]
res = nums[0]
for i in range(1, len(nums)):
mx = max_value
mn = min_value
max_value = max(nums[i], nums[i]*mx, nums[i]*mn)
min_value = min(nums[i], nums[i]*mx, nums[i]*mn)
print('==max_value:', max_value)
print('==min_value:', min_value)
res = max(max_value, res)
print('==res:', res)
nums = [2,3,-2,4]
sol = Solution()
sol.maxProduct(nums)150-2.三个数的最大乘积
思路:从小到大排序,如果都是正数则结果是最后三个相乘,如有正有负,结果有可能就是前两个相乘在乘以最后一个正数
class Solution:
def maximumProduct(self, nums):
nums = sorted(nums)
return max(nums[-1]*nums[-2]*nums[-3], nums[0]*nums[1]*nums[-1])
# nums = [1, 2, 3, 4]
nums = [-1, -2, 1, 2, 3]
sol = Solution()
sol.maximumProduct(nums)151.打家劫舍
class Solution(object):
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==0:
return 0
if len(nums)<2:
return max(nums)
opt = [0]*len(nums)
opt[0] = nums[0]
opt[1] = max(nums[0],nums[1])
for i in range(2, len(nums)):
opt[i] = max(opt[i-2]+nums[i],opt[i-1])
print('=opt:', opt)
return max(opt)
nums = [2,7,9,3,1]
sol = Solution()
sol.rob(nums)152.最长递增子序列的个数
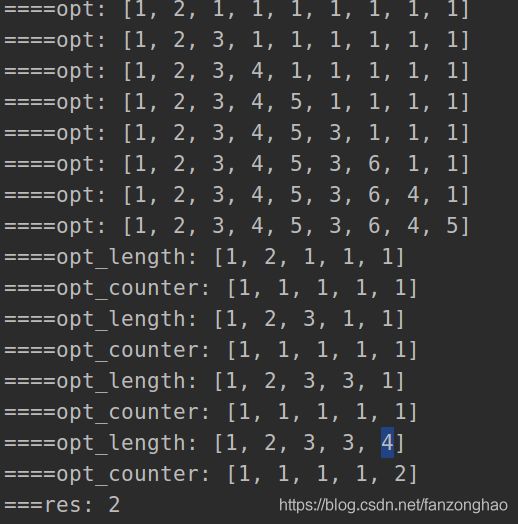
思路:利用dp,一个数组存储向上递增的长度,一个数组存储相同长度序列的个数
class Solution:
def findNumberOfLIS(self, nums):
if nums ==[]:
return(0)
n = len(nums)
opt_length = [1]*n
opt_counter = [1]*n
for i in range(1, n):
for j in range(i):
if nums[j] < nums[i]:
if opt_length[j]+1 > opt_length[i]:# 代表第一次遇到最长子序列
opt_length[i] = 1+opt_length[j]
opt_counter[i] = opt_counter[j]
elif opt_length[j]+1 == opt_length[i]:# 代表已经遇到过最长子序列
opt_counter[i] = opt_counter[i]+opt_counter[j]
# print('====opt_length:', opt_length)
# print('====opt_counter:', opt_counter)
tmp = max(opt_length)
res = sum([opt_counter[i] for i in range(n) if opt_length[i] == tmp])
return (res)
sol = Solution()
nums = [1, 3, 5, 4, 7]
res = sol.findNumberOfLIS(nums)
print('===res:', res)153-1.零钱兑换
思路:找准状态状转移方程,f代表选择银币的函数,则f(11)=f(11-1)+1或f(11)=f(11-2)+1或f(11)=f(11-5)+1,则一般方程为:
f(money) = min(f(money), f(money-coin)+1)
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
#状态转移方程f(money) = min(f(money),f(money-coin)+1)
f = [float('inf')] * (amount + 1)
f[0] = 0
# print('==f:', f)
for i in range(1, amount + 1):
for coin in coins:
if i - coin >= 0:
f[i] = min(f[i], f[i - coin] + 1)
# print('==f:', f)
return f[-1] if f[-1]!=float('inf') else -1
153-2:零钱兑换 II
思路1:回溯 会超时
# 组合问题 回溯 超时
class Solution:
def backtrace(self, amount, start, coins, track):
if amount == 0: # 终止条件
# self.res.append(track)
self.res+=1
return
for i in range(start, len(coins)): # 选择条件
if coins[i] > amount:
continue
# store = track.copy()
# track.append(coins[i])
self.backtrace(amount - coins[i], i, coins, track)
# track = store
def change(self, amount, coins):
self.res = 0#[]
coins = sorted(coins)
self.backtrace(amount, 0, coins, [])
return self.res
# amount = 5
# coins = [2]
amount = 5
coins = [1, 2, 5]
# amount = 500
# coins = [3,5,7,8,9,10,11]
sol = Solution()
res = sol.change(amount, coins)
print('==res:', res)
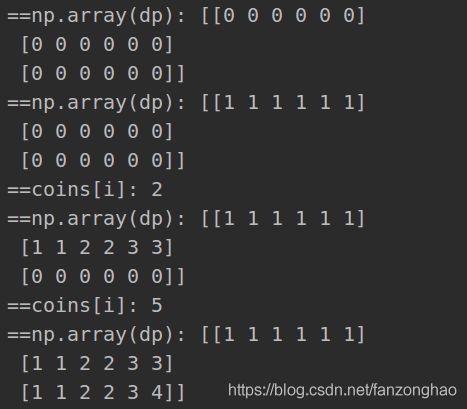
思路2:当成完全背包问题,用dp
#dp[i][j] 硬币为i 金额为j的组合数
import numpy as np
class Solution:
def change(self, amount, coins):
if len(coins) == 0:
if amount == 0:
return 1
else:
return 0
dp = [[0 for i in range(amount+1)] for j in range(len(coins))]
print('==np.array(dp):', np.array(dp))
dp[0][0] = 1
for j in range(coins[0], amount+1, coins[0]):
dp[0][j] = 1
print('==np.array(dp):', np.array(dp))
for i in range(1, len(coins)):
print('==coins[i]:', coins[i])
for j in range(amount+1):
dp[i][j] = dp[i - 1][j]#不选
if j >= coins[i]:#选 注意与0 1背包有一点不同
dp[i][j] += dp[i][j - coins[i]]
print('==np.array(dp):', np.array(dp))
return dp[-1][-1]
amount = 5
coins = [1, 2, 5]
sol = Solution()
sol.change(amount, coins)
154.跳跃游戏
方法1:贪心算法
思路:更新最长距离与数组索引
class Solution:
def canJump(self, nums: List[int]) -> bool:
reach = 0
for i in range(len(nums)):
if i>reach:
return False
reach = max(reach, nums[i]+i)
return True方法2:动态规划
class Solution(object):
def canJump(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
opt = [False]*len(nums)
opt[0] = True
for i in range(1,len(nums)):
opt[i] = opt[i-1] and nums[i-1] > 0
nums[i] = max(nums[i], nums[i-1]-1)#更新nums 最大距离
return opt[-1]155.移掉K位数字
思路:单调栈
class Solution(object):
def removeKdigits(self, num, k):
"""
:type num: str
:type k: int
:rtype: str
"""
#单调栈
stack = []
for digit in num:
while k and stack and stack[-1]>digit:
stack.pop()
k -= 1
stack.append(digit)
# print('==stack:', stack)
final_stack = stack[:-k] if k else stack
return "".join(final_stack).lstrip('0') or "0"156-1.单调递增的数字
class Solution(object):
def monotoneIncreasingDigits(self, N):
"""
:type N: int
:rtype: int
"""
digits = []
A = list(map(int, str(N)))
# print('==A:', A)
for i in range(len(A)):
for d in range(1, 10):
# print('==digits + [d] * (len(A) - i):', digits + [d] * (len(A) - i))
if digits + [d] * (len(A) - i) > A:
digits.append(d - 1)
break
else:
digits.append(9)
# print('==digits:', digits)
return int("".join(map(str, digits)))156-2:每日温度
思路:单调递增栈
class Solution:
def dailyTemperatures(self, T):
#单调递增栈
res = [0]*len(T)
stack = []
for i in range(len(T)):
while stack and T[i] > T[stack[-1]]:
res[stack[-1]] = i - stack[-1]
stack.pop()
print('==stack', stack)
print('==res:', res)
stack.append(i)
return res
T = [73, 74, 75, 71, 69, 72, 76, 73]
sol = Solution()
sol.dailyTemperatures(T)
157.无重叠区间
思路:贪心算法得到末端最小的数
class Solution(object):
def eraseOverlapIntervals(self, intervals):
"""
:type intervals: List[List[int]]
:rtype: int
"""
if len(intervals)==0:
return 0
intervals = sorted(intervals,key=lambda x:x[-1])
# print('intervals', intervals)
res = [intervals[0]]
for interval in intervals[1:]:
if res[-1][-1] <= interval[0]:
res.append(interval)
else:
pass
# print('res:',res)
return len(intervals) - len(res)158.插入区间
思路1:不断合并更新列表即可以
class Solution:
def insert(self, intervals, newInterval):
intervals.append(newInterval)
# print('==intervals:', intervals)
intervals = sorted(intervals, key=lambda x: (x[0], x[1]))
print('==intervals:', intervals)
index = 0
while index < len(intervals) - 1:
print('==index:', index)
print('==intervals:', intervals)
# 合并删除
if intervals[index][1] >= intervals[index + 1][0]:
intervals[index][1] = max(intervals[index][1], intervals[index + 1][1])
intervals.pop(index + 1)
else:
index += 1
return intervals
# intervals = [[1, 3], [6, 9]]
# newInterval = [2, 5]
intervals = [[1, 2], [3, 5], [6, 7], [8, 10], [12, 16]]
newInterval = [4, 8]
sol = Solution()
sol.insert(intervals, newInterval)思路2:开出一个新列表用于存储满足的即可
class Solution:
def insert(self, intervals, newInterval):
intervals.append(newInterval)
# print('==intervals:', intervals)
intervals = sorted(intervals, key=lambda x: (x[0], x[1]))
print('==intervals:', intervals)
merge = []
for interval in intervals:
if len(merge) == 0 or interval[0] > merge[-1][-1]:
merge.append(interval)
else:
merge[-1][-1] = max(merge[-1][-1], interval[-1])
print(merge)
return merge
# intervals = [[1, 3], [6, 9]]
# newInterval = [2, 5]
intervals = [[1, 2], [3, 5], [6, 7], [8, 10], [12, 16]]
newInterval = [4, 8]
sol = Solution()
sol.insert(intervals, newInterval)
159.合并区间
![]()
思路1:不断合并更新
class Solution:
def merge(self, intervals):
intervals = sorted(intervals, key=lambda x:(x[0], x[-1]))
index = 0
while index < len(intervals) - 1:
if intervals[index][-1] >= intervals[index + 1][0]:
intervals[index][-1] = max(intervals[index + 1][-1], intervals[index][-1])
intervals.pop(index + 1)
else:
index += 1
print('=intervals:', intervals)
return intervals
intervals = [[1, 3], [2, 6], [8, 10], [15, 18]]
# intervals = [[1,4],[0,4]]
sol = Solution()
sol.merge(intervals)思路2:开出新列表用于存储满足条件的数
class Solution:
def merge(self, intervals):
intervals= sorted(intervals,key= lambda x:(x[0],x[-1]))
print('==intervals:', intervals)
res = [intervals[0]]
for i in range(1, len(intervals)):
if intervals[i][0]<=res[-1][-1]:
res[-1][-1] = max(intervals[i][-1],res[-1][-1])
else:
res.append(intervals[i])
print('==res:', res)
return res
# intervals = [[1,3],[2,6],[8,10],[15,18]]
intervals = [[1,4],[2,3]]
sol = Solution()
sol.merge(intervals)160-1.买卖股票的最佳时机
思路1:动态规划用来存储最小和最大值之间差距
状态转移方程 不卖或者卖 opt[i] = max(opt[i-1], prices[i]-min_price)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) <= 1:
return 0
opt = len(prices)*[0]
min_price = prices[0]
for i in range(1, len(prices)):
if prices[i]思路2:就是存储最小最大值的差值即可
class Solution:
def maxProfit(self, prices: List[int]) -> int:
#dp[i] = max(dp[i-1],prices[i] - minprice)
if len(prices)<=0:
return 0
# dp = len(prices)*[0]
minprice = prices[0]
res = 0
for i in range(1,len(prices)):
if prices[i]思路3:利用单调递增栈,找到元素小于栈顶的,则更新此时的最大利润, 对于一直递增的要特意在prices增加一个负数 作为递增拐点
class Solution:
def maxProfit(self, prices):
if len(prices)<=1:
return 0
stack = []
res = 0
prices.append(-1)
# print('==prices:', prices)
for i in range(len(prices)):
while stack and prices[i] <= prices[stack[-1]]:
print('==stack:', stack)
res = max(res, prices[stack[-1]]-prices[stack[0]])
print('==res:', res)
stack.pop()
stack.append(i)
# print('==stack:', stack)
return res
prices = [7,1,5,3,6,4]
# prices = [1,2]
sol = Solution()
sol.maxProfit(prices)160-2.买卖股票的最佳时机 II
思路1:与上一题差异在于对次数没有限制,所以采用贪心算法,一直累加
class Solution:
def maxProfit(self, prices):
if len(prices)<=1:
return 0
# opt = len(prices)*[0]
res = 0
for i in range(1,len(prices)):
if prices[i]>prices[i-1]:
res+=prices[i]- prices[i-1]
print('===res:', res)
return res
prices = [7,1,5,3,6,4]
sol = Solution()
sol.maxProfit(prices)思路2:dp解法
dp存储有无的利润
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了
今天有股票:1.昨天有,今天不操作; 2.昨天无,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] =max(dp[i-1][1],dp[i-1][0]-prices[i])
class Solution:
def maxProfit(self, prices):
# res = 0
# for i in range(1, len(prices)):
# if prices[i]>prices[i-1]:
# res +=prices[i] - prices[i-1]
# return res
n = len(prices)
dp = [[0 for i in range(2)] for i in range(n)]
print('==dp:', dp)
dp[0][1] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
print('==dp:', dp)
return dp[-1][0]#返回没有的最大利润
prices = [7, 1, 5, 3, 6, 4]
sol = Solution()
sol.maxProfit(prices)160-3.买卖股票的最佳时机含手续费
dp解法: dp存储有无的利润
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了 在减去费用
今天有股票:1.昨天有,今天不操作; 2.昨天无,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)
dp[i][1] =max(dp[i-1][1],dp[i-1][0]-prices[i])
class Solution:
def maxProfit(self, prices, fee):
dp = [[0 for i in range(2)] for i in range(len(prices))]
dp[0][1] = -prices[0]
for i in range(1, len(prices)):
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee)
dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])
print('==dp:', dp)
return dp[-1][0]
prices = [1, 3, 2, 8, 4, 9]
fee = 2
sol = Solution()
sol.maxProfit(prices, fee)160-4.最佳买卖股票时机含冷冻期
思路:和上一题不用的是增加了冷冻期,故状态方程dp[i]不在由dp[i-1]来,而是dp[i-2]来的
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了
今天有股票:1.昨天有,今天不操作; 2.昨天是冷冻期,前天卖出,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] =max(dp[i-1][1],dp[i-2][0]-prices[i])
class Solution:
def maxProfit(self, prices):
if len(prices) <= 1:
return 0
dp = [[0 for i in range(2)] for i in range(len(prices))]
print('==dp:', dp)
dp[0][1] = -prices[0]
dp[1][0] = max(dp[1 - 1][0], dp[1 - 1][1] + prices[1])
dp[1][1] = max(dp[1-1][1], -prices[1])
for i in range(2, len(prices)):
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 2][0] - prices[i])
print('==dp:', dp)
return dp[-1][0]#返回没有的最大利润
prices = [1, 2, 3, 0, 2]
sol = Solution()
sol.maxProfit(prices)160-5.买卖股票的最佳时机 III
#dp[i][j][0] 不持有利润
#dp[i][j][1] 持有的利润
# i代表天数,j代表买入次数
#昨天可能持有也可能没有持有,昨天持有今天卖了dp[i-1][j][1]+prices[i],昨天没有dp[i-1][j][0]
#dp[i][j][0] = max(dp[i-1][j][0],dp[i-1][j][1]+prices[i])
#昨天持有也可能没有持有,昨天持有dp[i-1][j][1],昨天没有持有dp[i-1][j-1][0]-prices[i]
#dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i])
class Solution:
def maxProfit(self, prices):
#k代表交易次数,本题为0,1,2
n = len(prices)
k = 2
dp = [[[0, 0] for i in range(k+1)] for _ in range(n)]
for i in range(n):#边界条件1:第i天不买入是否持有的利润
dp[i][0][0] = 0
dp[i][0][1] = float('-inf')#用负无穷代表不可能
# print(dp)
for j in range(1, k+1):#边界条件2:第0天买入是否持有的利润
dp[0][j][0] = 0
dp[0][j][1] = -prices[0]
for i in range(1, n):
for j in range(1,k+1):
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i])
dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i])
return dp[-1][-1][0]
prices = [3,3,5,0,0,3,1,4]
sol = Solution()
sol.maxProfit(prices)
161.累加数
思路:两层for循环取出相应的值和剩下的值进行递归即可.
class Solution:
def backtrace(self, n1, n2, rest):
sum_ = str(int(n1)+int(n2))
if sum_ == rest:#找到满足的条件
return True
if len(sum_) > len(rest) or rest[:len(sum_)] != sum_:#找到不满足的条件
return False
else:
return self.backtrace(n2, sum_, rest[len(sum_):])
def isvalid_num(self, value):
"""以0开头,例如01,065"""
return len(value) > 1 and value[0] == '0'
def isAdditiveNumber(self, num):
if len(num) < 3:
return False
for i in range(1, len(num)):# 找到第一个数:num[:i]
for j in range(i + 1, len(num)):# 找到第二个数:num[i:j]
n1, n2, rest = num[:i], num[i:j], num[j:]# 剩下的数
# print('==n1, n2, rest:', n1, n2, rest)
if self.isvalid_num(n1) or self.isvalid_num(n2) or self.isvalid_num(rest): # 避免0开头的非0数
continue
if self.backtrace(n1, n2, rest):
return True
return False
num = "112358"
sol = Solution()
res = sol.isAdditiveNumber(num)
print('res:', res)162.克隆图
思路:BFS遍历每个节点
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return node
visited = {}#存储遍历过的节点
visited[node] = Node(node.val, [])
quene = [node]
while quene:
pop_node = quene.pop()
for neighbor in pop_node.neighbors:
if neighbor not in visited:#没有遍历过
visited[neighbor] = Node(neighbor.val, [])
quene.append(neighbor)
# 更新当前节点的邻居列表
visited[pop_node].neighbors.append(visited[neighbor])
return visited[node]
163.被围绕的区域
思路:从边界的'O'回退,找到依次相邻的O则不动,否则置为'X'
# 从边界的'O'回退,找到依次相邻的O则不动,否则置为'X'
class Solution:
def helper(self, i, j, h, w):
if not 0 <= i < h or not 0 <= j < w or self.board[i][j] != 'O':
return
self.board[i][j] = 'F'
self.helper(i - 1, j, h, w)
self.helper(i + 1, j, h, w)
self.helper(i, j-1, h, w)
self.helper(i, j+1, h, w)
def solve(self, board):
"""
Do not return anything, modify board in-place instead.
"""
self.board = board
h, w = len(self.board), len(self.board[0])
for i in range(h):
self.helper(i, 0, h, w)
self.helper(i, w - 1, h, w)
print('==self.board:', self.board)
for j in range(1, w-1):
self.helper(0, j, h, w)
self.helper(h-1, j, h, w)
print('==self.board:', self.board)
for i in range(h):
for j in range(w):
if self.board[i][j] == "F":
self.board[i][j] = "O"
elif self.board[i][j] == "O":
self.board[i][j] = "X"
print('==self.board:', self.board)
return self.board
board = [["X", "X", "X", "X"],
["X", "O", "O", "X"],
["X", "X", "O", "X"],
["X", "O", "X", "X"]]
# board = [["X", "X", "X"],
# ["X", "O", "O"],
# ["X", "X", "O"],
# ["X", "O", "X"]]
sol = Solution()
sol.solve(board)164.岛屿数量
思路:递归 也就是求1的连通域个数,从1开始进行遍历,将遍历过得1依次置位0,遍历的次数就是连通域个数
# 求1的连通域个数,从1开始进行遍历,将遍历过得1依次置位0,遍历的次数就是连通域个数
class Solution:
def helper(self, i, j, h, w):
if i < 0 or i >= h or j < 0 or j >= w or self.grid[i][j] == "0":
return
self.grid[i][j] = "0"
self.helper(i - 1, j, h, w)
self.helper(i + 1, j, h, w)
self.helper(i, j-1, h, w)
self.helper(i, j+1, h, w)
def numIslands(self, grid):
if len(grid) == 0:
return []
self.grid = grid
h, w = len(grid), len(grid[0])
nums = 0
for i in range(h):
for j in range(w):
if self.grid[i][j] == "1":
nums += 1
self.helper(i, j, h, w)
print('==self.grid:', self.grid)
print('==nums:', nums)
return nums
grid = [
["1", "1", "1", "1", "0"],
["1", "1", "0", "1", "0"],
["1", "1", "0", "0", "0"],
["0", "0", "0", "0", "0"]
]
sol = Solution()
sol.numIslands(grid)
165-1. 单词拆分
思路1:动态规划
#动态规划 dp[i]表示 s 的前 i 位是否可以用 wordDict 中的单词表示,
#
class Solution:
def wordBreak(self, s, wordDict):
n = len(s)
dp = [False] * (n + 1)
dp[0] = True
for i in range(n):
for j in range(i+1, n+1):
if dp[i] and (s[i:j] in wordDict):
dp[j] = True
print('==dp:', dp)
return dp[-1]
s = "leetcode"
wordDict = ["leet", "code"]
sol = Solution()
res= sol.wordBreak(s, wordDict)
print('==res:', res)
思路2:回溯加缓存
#递归 lru_cache用于缓存 将数据缓存下来 加快后续的数据获取 相同参数调用时直接返回上一次的结果
import functools
class Solution:
@functools.lru_cache()
def helper(self, s):
if len(s) == 0:
return True
res = False
for i in range(1, len(s)+1):
if s[:i] in self.wordDict:
res = self.helper(s[i:]) or res
return res
def wordBreak(self, s, wordDict):
self.wordDict = wordDict
return self.helper(s)
s = "leetcode"
wordDict = ["leet", "code"]
# s = "aaaaaaa"
# wordDict = ["aaaa", "aaa"]
# s= "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
# wordDict = ["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"]
sol = Solution()
res= sol.wordBreak(s, wordDict)
print('==res:', res)
165-2.单词拆分 II
思路:递归
class Solution:
def helper(self, s, wordDict, memo):
if s in memo:#递归终止条件
return memo[s]
if s=='':#递归终止条件
return []
res = []
for word in wordDict:
if not s.startswith(word):
continue
if len(word)==len(s):#匹配上刚好相等
res.append(word)
else:#匹配上 但是字符还没到最后
rest = self.helper(s[len(word):], wordDict, memo)
for tmp in rest:
tmp = word+ " "+ tmp
res.append(tmp)
print('==res:', res)
print('==memo:', memo)
memo[s] = res
return res
def wordBreak(self, s, wordDict):
if s=='':
return []
return self.helper(s, wordDict, memo={})
s = "catsanddog"
wordDict = ["and", "cat", "cats", "sand", "dog"]
# s = "cat"
# wordDict = ["cat"]
sol = Solution()
res = sol.wordBreak(s, wordDict)
print(res)
166-1.回文子串
思路1:两层for循环遍历进行判断是否是回文字符串即可,超出时间限制
#双层for循环超出时间限制
class Solution:
def judge_palindrome(self, s):
l = 0
r = len(s) -1
while l<=r:
if s[l]==s[r]:
l+=1
r-=1
else:
return False
return True
def countSubstrings(self, s):
res=0
for i in range(len(s)):
# print('==i:', i)
for j in range(i, len(s)):
# print('==j', j)
# print('==s[i:j+1]:', s[i:j+1])
if self.judge_palindrome(s[i:j+1]):
res += 1
return res
# s = "abc"
s = "aaa"
sol = Solution()
res = sol.countSubstrings(s)
print('==res:', res)
思路2,中心枚举,专门用self.res存储 left与righe索引方便查看,,最后求和就是会文字符串的个数。
import numpy as np
class Solution:
def helper(self,left,right,s):
while left>=0 and right166-2:回文串分割 IV
思路:中心枚举 用一个矩阵存储回文字符串左右索引的值,最后看看是不是分为三段即可
import numpy as np
class Solution:
def helper(self,left,right,s):
while left>=0 and right166-3.最长回文子串
class Solution:
def helper(self,left,right,s):
while left>=0 and rightlen(self.res):
self.res = s[left+1:right]
def longestPalindrome(self, s: str) -> str:
self.res = ''
for i in range(len(s)):
self.helper(i,i,s)
self.helper(i,i+1,s)
return self.res
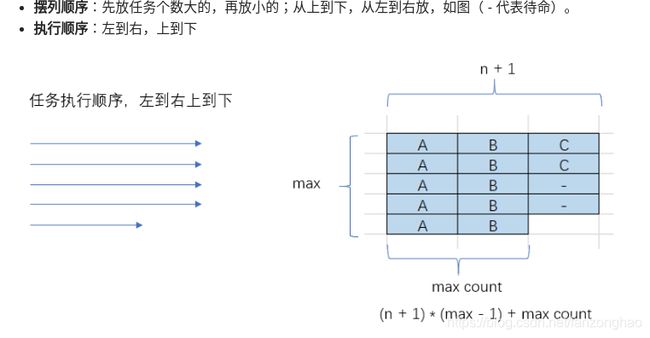
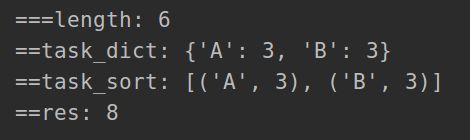
167.任务调度器
思路: 填桶法
class Solution(object):
def leastInterval(self, tasks, n):
"""
:type tasks: List[str]
:type n: int
:rtype: int
"""
length = len(tasks)
if length <= 1:
return length
print('===length:', length)
# 用于记录每个任务出现的次数
task_dict = {}
for task in tasks:#不存在task时 返回0
task_dict[task] = task_dict.get(task,0)+1
print('==task_dict:', task_dict)
# 按任务出现的次数从大到小排序
task_sort = sorted(task_dict.items(), key=lambda x: x[1], reverse=True)
print('==task_sort:', task_sort)
# # 出现最多次任务的次数
max_task_count = task_sort[0][1]
# 至少需要的最短时间
res = (max_task_count - 1) * (n + 1)
for sort in task_sort:
if sort[1] == max_task_count:
res += 1
print('==res:', res)
# # 如果结果比任务数量少,则返回总任务数
return res if res >= length else length
tasks = ["A","A","A","B","B","B"]
n = 2
# n = 0
sol = Solution()
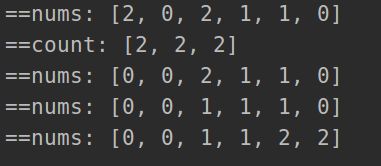
sol.leastInterval(tasks, n)168.最短无序连续子数组
思路1:单调递增栈
class Solution:
def findUnsortedSubarray(self, nums):
#找到递增的拐点
stack = []
left = len(nums)-1
for i in range(len(nums)):
while stack and nums[i] < nums[stack[-1]]:
index = stack.pop()
left = min(left, index)
stack.append(i)
print('==stack:', stack)
print('left:', left)
#找到逆序递增的拐点
stack = []
right = 0
for i in range(len(nums)-1, -1, -1):
while stack and nums[i] > nums[stack[-1]]:
index = stack.pop()
right = max(right, index)
stack.append(i)
print('==right:', right)
return right-left+1 if right-left>0 else 0
nums = [2, 6, 4, 8, 10, 9, 15]
# nums = [2, 1, 6]
# nums = [1, 2]
# nums = [2, 1]
# nums = [5, 4, 3, 2, 1]
sol = Solution()
res = sol.findUnsortedSubarray(nums)
print('======res:', res)思路2:排序
class Solution:
def findUnsortedSubarray(self, nums: List[int]) -> int:
# print('==nums:', nums)
sort_nums = sorted(nums)
# print('==sort_nums:', sort_nums)
left = len(nums) - 1
right = 0
for i in range(len(nums)):
if nums[i] != sort_nums[i]:
left = min(left, i)
right = max(right, i)
# print('==left:', left)
# print('==right:', right)
return right - left + 1 if right - left > 0 else 0169.和为K的子数组
思路1:枚举(超时) O(n2)
class Solution:
def subarraySum(self, nums, k):
res=0
for i in range(len(nums)):
tmp = 0
for j in range(i,len(nums)):
tmp+=nums[j]
if tmp==k:
res+=1
print('=res:',res)
return res
# nums = [1,1,1]
# k = 2
nums = [1,-1,0]
k = 0
sol = Solution()
sol.subarraySum(nums, k)
思路2:hash,利用字典的key值存储累加和,value值存储出现次数
#利用字典 key存储累加的数字 value为出现的次数
class Solution:
def subarraySum(self, nums, k):
count_dict = {}
count, sum_ = 0, 0
for num in nums:
sum_+=num
if sum_==k:
count+=1
if sum_-k in count_dict:
count+=count_dict[sum_-k]
if sum_ in count_dict:
count_dict[sum_]+=1
else:
count_dict[sum_]=1
print('==count_dict:', count_dict)
print('count:', count)
return count
nums = [1, 1, 1]
k = 2
# nums = [1, -1, 1]
# k = 0
sol = Solution()
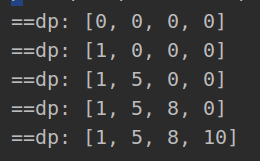
sol.subarraySum(nums, k)171.目标和
思路2:动态规划 dp[i][j]表示到i为止,数字和为j的方案数,下面以两个例子为例
# dp[i][j] = dp[i-1][j-nums[i]]+dp[i-1][j+nums[i]]
class Solution:
def findTargetSumWays(self, nums, S):
sum_ = sum(nums)
if abs(S) > sum_:
return 0
opt = [[0 for i in range(2 * sum_ + 1)] for i in range(len(nums))]
print(np.array(opt))
##nums = [0,0,0,0,0,0,0,0,1]
# S = 1
if nums[0] == 0: # 边界条件
opt[0][sum_] = 2
else:
opt[0][sum_ - nums[0]] = 1
opt[0][sum_ + nums[0]] = 1
print(np.array(opt))
for i in range(1, len(nums)):
for j in range(2 * sum_ + 1):
l = j - nums[i] if j - nums[i] > 0 else 0
r = j + nums[i] if j + nums[i] < 2 * sum_ + 1 else 0
opt[i][j] = opt[i - 1][l] + opt[i - 1][r]
# print('===print(np.array(opt)):', np.array(opt))
return opt[-1][sum_ + S]
# nums = [1, 1, 1, 1, 1]
# S = 3
# nums = [1000]
# S = 1000
nums = [0, 0, 0, 0, 0, 0, 0, 0, 1]
S = 1
sol = Solution()
res = sol.findTargetSumWays(nums, S)
print('==res:', res)172.分割等和子集
思路1:
(1)转换成0 1背包问题,找到数组和的一半的子集
(2)dp[i][j]表示到i为止和为j是否存在
(3)dp[i][j] = dp[i-1][j] 不选择nums[i]
(4)dp[i][j] = dp[i-1][j-nums] 选择nums[i]
(5)如果 j 以[1,2,3,6]为例 思路2:优化版 用一维数组替代,只不过采用逆序 其中dp[j] = dp[j] || dp[j - nums[i]] 可以理解为 dp[j] (新)= dp[j] (旧) || dp[j - nums[i]] (旧),如果采用正序的话 dp[j - nums[i]]会被之前的操作更新为新值 173.汉明距离 思路:通过异或取得不同数的 在向右移动 依次与1进行& 获得1的个数 174.找到所有数组中消失的数字 思路1:hash 思路2:原地修改 175.一和零 思路:当成 0 1背包问题来做,只不过这道题需要两个背包一个是装0的,一个是装1的,求在装满的时候的最大字符串量 使用i为止这个字符串 j个0 k个1 能够容纳的最多字符串 dp[i][j][k] = dp[i-1][j][k] 不选这个字符串 dp[i][j][k] = dp[i-1][j-cnt[0]][k-cnt[1]] 选这个字符串 cnt[0]代表0的个数 cnt[1]代表1的个数 代码1:需要初始化第一个字符串的dp 代码2:多生成一个字符串空间dp,就不需要初始化第一个字符串 177.除法求值 思路1:并查集 思路2:dfs 递归 178.移动零 思路1:移0法 思路2:指针记录非0索引 思路3:指针 交换数字 思路4:优化特殊非0元素 179.字符串解码 思路:栈 180.前 K 个高频元素 思路:hash字典 181.两地调度问题 1.贪心算法未优化版 2.贪心算法优化版 182.颜色分类 思路1:单指针法:先将0进行交换放在第一位,再将1进行交换放在0后面 思路2:计数排序:对每种颜色进行计数,然后根据个数去修改nums数组 183.比特位计数 思路: 184. 打家劫舍 III 185.合并两个有序数组 思路:归并排序中的并 187.寻找重复数 思路:对于上述题目示例1,将数组值作为索引,会发现陷入无穷循环,而无穷循环的起始点就是重复出现的数,故构成一个环,所以就想到用快慢指针进行解决,如下图所示,A是起点,B是环开始点,C是相遇点,快指针是慢指针速度的两倍。 在C点相遇以后,在从起始点和C点用相同速度奔跑,就在B点相遇了,即可以得到重复的数字。 188.移除无效的括号 思路:栈用来保存索引和相应的左右括号 189.转置矩阵 思路1.开辟二维数组 思路2:用zip 190.除自身以外数组的乘积 思路1:超时 思路2:利用空间换时间 1.借用左右数组来存储值,L[i]代表i左边的乘积值,R[i]代表i右边的乘积值 2.最终i处的值为L[i]*R[i] 191.大正方形 思路:题目既然求最大正方形面积,那就先由2*2正方形拓展更大即可,也就是可以用动态规划来存储左上角,左边,上边的最小值,也是正方形边长 1.转移方程为 dp[i][j] = min(dp[i-1][j],dp[i][j-1].dp[i-1][j-1])+1 2.初始化边界条件为: dp[:][0] = matrix[:][0] dp[0][:] = matrix[0][:] 192.实现 Trie (前缀树) 思路:利用字典存储每个单词,同时用特殊字符结尾。 193.面试题 08.13. 堆箱子 思路:其实就是在找最长上升子序列 可以将箱子先从小到大排序 在寻找最长子序列 194.LRU 缓存机制 195.最长连续序列 198.字符串中的第一个唯一字符 思路:利用hash统计每个字符出现的个数,在判断hash中字符个数为1的字母,即找到 199.分发糖果 思路:从左往右找递增 在从右往左找递增![]()
#转换成0 1背包问题 找到数组和的一半的子集
#到i为止和为j是否存在
#dp[i][j] = dp[i-1][j]#不选择nums[i]
#dp[i][j] = dp[i-1][j-nums]#选择nums[i]
#如果 j
import numpy as np
#转换成0 1背包问题 找到数组和的一半的子集
#优化版
#dp[j] = [j]#不选择nums[i]
#dp[j] = dp[j-nums]#选择nums[i]
# #如果 j
#思路:通过异或取得不同数的 在向右移动 依次与1进行& 获得1的个数
class Solution:
def hammingDistance(self, x, y):
res = x ^ y#异或取得不同的数 异或 相同为0 不同为1
# print('==res:', res)
dis = 0
while res:#向右移位
# print('==res&1:', res&1)
if res&1:
dis+=1
res = res>>1
# print('==res:', res)
return dis
x = 1
y = 4
sol = Solution()
sol.hammingDistance(x, y)
#利用hash存储出现过得数字
class Solution:
def findDisappearedNumbers(self, nums):
dict_ = {}
for num in nums:
dict_[num] = dict_.get(num, 0)+1
print('==dict_:', dict_)
res =[]
for i in range(1, len(nums)+1):
if i not in dict_:
res.append(i)
return res
nums = [4,3,2,7,8,2,3,1]
sol = Solution()
res = sol.findDisappearedNumbers(nums)
print('==res:', res)
#利用list原地进行修改
class Solution:
def findDisappearedNumbers(self, nums):
for i in range(len(nums)):
index = abs(nums[i]) - 1
if nums[index] > 0:
nums[index] *= -1
print('==nums:', nums)
res =[]
for i in range(len(nums)):
if nums[i]>0:
res.append(i+1)
return res
nums = [4,3,2,7,8,2,3,1]
# nums = [1, 3, 3, 4, 5]
sol = Solution()
res = sol.findDisappearedNumbers(nums)
print('==res:', res)
import numpy as np
class Solution:
def count(self, str_):
cnt= [0, 0]
for i in str_:
cnt[int(i) - 0] += 1
return cnt
def findMaxForm(self, strs, m, n):
dp = [[[0 for _ in range(n+1)] for _ in range(m+1)] for _ in range(len(strs))]
print(np.array(dp).shape)
cnt = self.count(strs[0])
#对第一件物品进行初始化
for j in range(m+1):
for k in range(n+1):
dp[0][j][k] = 1 if j >= cnt[0] and k >= cnt[1] else 0
print(np.array(dp).shape)
for i in range(1, len(strs)):
# print('==strs[i]:', strs[i])
cnt = self.count(strs[i])
print('==cnt', cnt)
for j in range(m+1):
for k in range(n+1):
if (j - cnt[0])<0 or (k - cnt[1])<0:
dp[i][j][k] = dp[i - 1][j][k]
else:
dp[i][j][k] = max(dp[i-1][j][k], dp[i - 1][j - cnt[0]][k - cnt[1]]+1)
print(np.array(dp))
return dp[len(strs)-1][m][n]
strs = ["10", "0001", "111001", "1", "0"]
m = 5#0
n = 3#1
sol = Solution()
res= sol.findMaxForm(strs, m, n)
print('res:',res)
# 使用i为止这个字符串 j个0 k个1 能够容纳的最多字符串
# dp[i][j][k] = dp[i-1][j][k] 不选这个字符串
# dp[i][j][k] = dp[i-1][j-cnt[0]][k-cnt[1]] 选这个字符串
import numpy as np
class Solution:
def count(self, str_):
cnt= [0, 0]
for i in str_:
cnt[int(i) - 0] += 1
return cnt
def findMaxForm(self, strs, m, n):
dp = [[[0 for _ in range(n+1)] for _ in range(m+1)] for _ in range(len(strs)+1)]
print(np.array(dp).shape)
for i in range(1, len(strs)+1):
# print('==strs[i]:', strs[i])
cnt = self.count(strs[i-1])
print('==cnt', cnt)
for j in range(m+1):
for k in range(n+1):
if (j - cnt[0])<0 or (k - cnt[1])<0:
dp[i][j][k] = dp[i - 1][j][k]
else:
dp[i][j][k] = max(dp[i-1][j][k], dp[i - 1][j - cnt[0]][k - cnt[1]]+1)
print(np.array(dp))
return dp[len(strs)][m][n]
# 并查集
class Solution:
def calcEquation(self, equations, values, queries):
f = {}#每个节点的依次关系
d = {}#每个节点的值 将根节点值置为1
def find(x):#查找与你连通的最上面一位
f.setdefault(x, x)
d.setdefault(x, 1)
print('===f:', f)
print('===d:', d)
if x != f[x]:
t = f[x]
f[x] = find(t)
d[x] *= d[t]
return f[x]
return x
def union(A, B, value):#合并集
a, b = find(A), find(B)
print('==a, b:', a, b)
print('===f===:', f)
print('===d===:', d)
if a != b:
f[a] = b
d[a] = d[B] / d[A] * value
# print('===f===:', f)
# print('===d===:', d)
def check(x, y):
if x not in f or y not in f:
return -1.0
a, b = find(x), find(y)
print('==a, b:', a, b)
if a != b:#如果不在同一条线上就返回-1
return -1.0
return d[x] / d[y]
for i, nums in enumerate(equations):
union(nums[0], nums[1], values[i])
print('===f:', f)
print('===d:', d)
res = []
for x, y in queries:
res.append(check(x, y))
return res
equations = [["a","b"],["b","c"]]
values = [2.0,3.0]
queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
# equations = [["a","b"]]
# values = [2.0]
# queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
sol = Solution()
res = sol.calcEquation(equations, values, queries)
print('==res:', res)
# 思路:用字典创建图,然后dfs进行遍历
class Solution:
def calcEquation(self, equations, values, queries):
from collections import defaultdict
# 先创建图
graph = defaultdict(dict)
for (x, y), val in zip(equations, values):
'''
if x in graph:
graph[x][y] = val
else:
graph[x] = {y:val}
if y in graph:
graph[y][x] = 1/val
else:
graph[y] = {x:1/val}
'''
graph[x][y] = val
graph[y][x] = 1 / val
print('==graph:', graph)
res = []
for start, end in queries:
visited = set()
res.append(self.dfs(start, end, visited, graph))
return res
# dfs实现
def dfs(self, start, end, visited, graph):
visited.add(start) # 第一个点先加进visited,如果不加对结果没影响因为a/b * b/a = 1 但是别的题会错
if start not in graph: return -1
if start == end: return 1
for w in graph[start]:
if w == end:
return graph[start][w]
elif w not in visited:
visited.add(w)
v = self.dfs(w, end, visited,
graph) # dfs就是每次只做分内事,剩下的交给recursion来跑,但这题应该是‘如果跑出不是-1的就进行计算’,而不是‘跑出-1就说这个值计算不了’。
# print(v)
if v != -1:
return graph[start][w] * v
else:
pass # 这里不能return -1 因为会‘死路’但实际上走别的节点可以‘出路’,不能走一条死路就判断整体不存在
return -1 # 都失败了才是-1
equations = [["a", "b"], ["b", "c"]]
values = [2.0, 3.0]
queries = [["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"]]
sol = Solution()
sol.calcEquation(equations, values, queries)![]()
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
i=0
while 0 in nums:
nums.remove(0)
i+=1
nums.extend([0]*i)
return nums
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
nums[idx] = nums[i]
idx+=1
nums[idx:] = (n - idx )*[0]
return nums
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
nums[idx], nums[i] = nums[i], nums[idx]
idx+=1
# print(idx)
# print(nums)
# nums[idx:] = (n - idx )*[0]
return nums
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
idx = 0
n = len(nums)
for i in range(len(nums)):
if nums[i]!=0:
if i!=idx:
nums[idx], nums[i] = nums[i], nums[idx]
idx+=1
else:
idx +=1
# print(idx)
# print(nums)
# nums[idx:] = (n - idx )*[0]
return nums
class Solution:
def decodeString(self, s):
stack = [] # (str, int) 记录之前的字符串和括号外的上一个数字
num = 0
res = "" # 实时记录当前可以提取出来的字符串
for c in s:
if c.isdigit():
num = num * 10 + int(c)
elif c == "[":
stack.append((res, num))
res, num = "", 0
elif c == "]":
top = stack.pop()
print('===top:', top)
res = top[0] + res * top[1]
print('==res:', res)
else:
res += c
return res
# s = "3[a]2[bc]"
s = "3[a2[c]]"
sol = Solution()
res = sol.decodeString(s)
print('res:', res)
class Solution:
def topKFrequent(self, nums, k):
dict_ = {}
for num in nums:
dict_[num] = dict_.get(num, 0)+1
print('==dict_:', dict_)
sort_dict = sorted(dict_.items(), key=lambda x:(x[-1], x[0]), reverse=True)
return [sort_dict[j][0] for j in range(k)]
# nums = [1,1,1,2,2,3]
# k = 2
nums = [-1, -1]
k = 1
# nums = [1, 2]
# k = 2
sol = Solution()
res = sol.topKFrequent(nums, k)
print('==res:', res)# 贪心算法:
#思路:对AB两地的费用之差绝对值排序,利用贪心算法选择最小费用的城市,当最小费用的城市人满了以后,剩下的人就去另外一个城市
class Solution:
def twocitycost(self, costs):
# 对差值进行排序
costs = sorted(costs, key=lambda x: abs(x[0] - x[1]), reverse=True)
print('==costs:', costs)
total_cost = 0
toA, toB = 0, 0
every_city_person = len(costs) // 2
for i, cost in enumerate(costs):
if toA < every_city_person and toB < every_city_person:
if cost[0] < cost[-1]: # A地未去满同时A地的费用最小
toA = +1
total_cost += cost[0]
else: # B地未去满同时B地的费用最小
toB = +1
total_cost += cost[-1]
elif toA
#优化版
#思路:对AB两地的费用之差排序,自然前面的人费用最小 后面的人费用最大
class Solution:
def twocitycost(self, costs):
# 对差值进行排序
costs = sorted(costs, key=lambda x: x[0] - x[1])
print('==costs:', costs)
total_cost = 0
every_city_person = len(costs) // 2
for i in range(every_city_person):
total_cost+=costs[i][0]+costs[i+every_city_person][-1]
print('==total_cost:', total_cost)
return total_cost
costs = [[10, 20], [30, 200], [400, 50], [30, 20]]
sol = Solution()
sol.twocitycost(costs)
# 单指针法:先将0进行交换放在第一位,再将1进行交换放在0后面
class Solution:
def sortColors(self, nums):
"""
Do not return anything, modify nums in-place instead.
"""
# 先将0进行交换放在第一位
start = 0
for i in range(len(nums)):
if nums[i] == 0:
nums[i], nums[start] = nums[start], nums[i]
start += 1
# 再将1进行交换放在0后面
for i in range(len(nums)):
if nums[i] == 1:
nums[i], nums[start] = nums[start], nums[i]
start += 1
print('==nums:', nums)
return nums
nums = [2, 0, 2, 1, 1, 0]
sol = Solution()
sol.sortColors(nums)
class Solution:
def sortColors(self, nums):
print('==nums:', nums)
count = [0] * 3
for i in range(len(nums)):
if nums[i] == 0:
count[0] += 1
elif nums[i] == 1:
count[1] += 1
else:
count[-1] += 1
print('==count:', count)
p = 0
for i in range(len(count)):
num = count[i]
while num>0:
nums[p] = i
num-=1
p += 1
print('==nums:', nums)
return nums
nums = [2, 0, 2, 1, 1, 0]
sol = Solution()
sol.sortColors(nums)#思路:计算n的时候n-1计算过了
#n&n-1 就是抹掉二进制n最右边的1
class Solution:
def countBits(self, num):
#动态规划
res = [0]*(num+1)
for i in range(1, num+1):
res[i] = res[i & i-1] + 1
return res
num = 5
sol = Solution()
res = sol.countBits(num)
print('==res:', res)# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def helper(self,node):
if node is None:
return 0, 0
choose_l_value,no_choose_l_value = self.helper(node.left)
choose_r_value,no_choose_r_value = self.helper(node.right)
return node.val+no_choose_l_value+no_choose_r_value, max(choose_l_value,no_choose_l_value)+max(choose_r_value,no_choose_r_value)
def rob(self, root: TreeNode) -> int:
return max(self.helper(root))
#思路:归并排序中的并
class Solution:
def merge(self, nums1, m, nums2, n):
"""
Do not return anything, modify nums1 in-place instead.
"""
l, r = 0, 0
nums1_copy = nums1[:m].copy()
nums1 = []
while lclass Solution:
def findDuplicate(self, nums: List[int]) -> int:
fast = 0
slow = 0
while True:
# print('==fast:', fast)
# print('==slow:', slow)
fast = nums[nums[fast]]
slow = nums[slow]
if fast == slow:
break
start = 0
while True:
start = nums[start]
fast = nums[fast]
if start ==fast:
break
# print(start)
return start
class Solution:
def minRemoveToMakeValid(self, s):
stack = []
for i in range(len(s)):
# print('===s[i]==', s[i])
# print('==i, stack:', i, stack)
if s[i] == '(':
stack.append((i, '('))
elif s[i] == ')':
if len(stack) and stack[-1][-1]=='(':
stack.pop()
else:
stack.append((i, ')'))
else:
pass
# print('===stack', stack)
stack_index = [i[0] for i in stack]
res = ''
for i in range(len(s)):
if i not in stack_index:
res+=s[i]
# print('==res:', res)
return res
s = "a)b(c)d"
# s = "lee(t(c)o)de)"
# s = "))(("
sol = Solution()
sol.minRemoveToMakeValid(s)import numpy as np
class Solution:
def transpose(self, A):
print(np.array(A))
rows = len(A)
cols = len(A[0])
res = [[0] * rows for _ in range(cols)]
print(np.array(res))
for i in range(rows):
for j in range(cols):
res[j][i] = A[i][j]
print(np.array(res))
return res
A = [[1,2,3],[4,5,6]]
sol = Solution()
res = sol.transpose(A)
print('==res:', res)class Solution:
def transpose(self, A: List[List[int]]) -> List[List[int]]:
return list(zip(*A))
#超时时间复杂度O(N)
class Solution:
def productExceptSelf(self, nums):
output = len(nums)*[0]
for i in range(len(nums)):
temp = 1
for j in nums[:i]:
temp*=j
for j in nums[i+1:]:
temp*=j
output[i] = temp
# print('==output:', output)
return output
nums = [1, 2, 3, 4]
sol = Solution()
sol.productExceptSelf(nums)class Solution:
def productExceptSelf(self, nums):
length = len(nums)
L,R,output = [0]*length,[0]*length,[0]*length
L[0] = 1
for i in range(1, length):
L[i] = L[i-1]*nums[i-1]
print('==L:', L)
R[length-1] = 1
for i in reversed(range(length-1)):
print('==i:', i)
R[i] = R[i + 1] * nums[i + 1]
print('==R:', R)
for i in range(length):
output[i] = L[i]*R[i]
return output
nums = [1, 2, 3, 4]
sol = Solution()
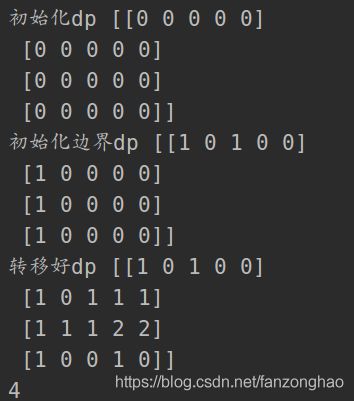
sol.productExceptSelf(nums)class Solution:
def maximalSquare(self, matrix):
max_side = 0
h,w = len(matrix),len(matrix[0])
dp = [[0 for i in range(w)] for i in range(h)]
print('初始化dp',np.array(dp))
for i in range(h):
dp[i][0] = int(matrix[i][0])
max_side = max(max_side, dp[i][0])
for i in range(w):
dp[0][i] = int(matrix[0][i])
max_side = max(max_side, dp[0][i])
print('初始化边界dp',np.array(dp))
for i in range(1,h):
for j in range(1,w):
if matrix[i][j]=='1':
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
max_side = max(max_side, dp[i][j])
print('转移好dp',np.array(dp))
return max_side**2
matrix = [["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]]
# matrix = [["0","1"],["1","0"]]
sol = Solution()
res= sol.maximalSquare(matrix)
print(res)
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = {}
self.word_end = -1
def insert(self, word):
"""
Inserts a word into the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
curNode[c] = {}
curNode = curNode[c]
curNode[self.word_end] = True
# print('==curNode:', curNode)
def search(self, word):
"""
Retu
rns if the word is in the trie.
"""
curNode = self.root
for c in word:
if c not in curNode:
return False
curNode = curNode[c]
if self.word_end not in curNode:
return False
return True
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
curNode = self.root
for c in prefix:
if c not in curNode:
return False
curNode = curNode[c]
return True
word = 'apple'
prefix = 'ad'
obj = Trie()
obj.insert(word='apple')
obj.insert(word='add')
# obj.insert(word='app')
print('tree:', obj.root)
param_2 = obj.search(word)
print('search res:', param_2)
param_3 = obj.startsWith(prefix)
print('==param_3:', param_3)#dp[i] 代表以第 i 个箱子放在最底下的最大高度
class Solution:
def pileBox(self, box):
dp = [0]*len(box)
print('==dp:', dp)
box = sorted(box)
# print('=box:', box)
for i in range(len(box)):
dp[i] = box[i][-1]
for j in range(i):
if box[i][0] > box[j][0] and box[i][1] > box[j][1] and box[i][-1] > box[j][-1]:
dp[i] = max(dp[i], dp[j]+box[i][-1])
print('==dp:', dp)
return max(dp)
# box = [[1, 1, 1], [2, 2, 2], [3, 3, 3]]
box = [[1, 1, 1], [2, 3, 4], [3, 4, 5],[2, 6, 7]]
sol = Solution()
sol.pileBox(box)
class DLinkedNode:
def __init__(self, key=0, value=0):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity):
self.cache = dict()
# 使用伪头部和伪尾部节点
self.head = DLinkedNode()
self.tail = DLinkedNode()
self.head.next = self.tail
self.tail.prev = self.head
self.capacity = capacity
self.size = 0
def get(self, key):
if key not in self.cache:
return -1
# 如果 key 存在,先通过哈希表定位,再移到头部
node = self.cache[key]
self.moveToHead(node)
return node.value
def put(self, key, value):
if key not in self.cache:
# 如果 key 不存在,创建一个新的节点
node = DLinkedNode(key, value)
# 添加进哈希表
self.cache[key] = node
# 添加至双向链表的头部
self.addToHead(node)
self.size += 1
if self.size > self.capacity:
# 如果超出容量,删除双向链表的尾部节点
removed = self.removeTail()
# 删除哈希表中对应的项
self.cache.pop(removed.key)
self.size -= 1
else:
# 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node = self.cache[key]
node.value = value
self.moveToHead(node)
def addToHead(self, node):
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node
self.head.next = node
def removeNode(self, node):
node.prev.next = node.next
node.next.prev = node.prev
def moveToHead(self, node):
self.removeNode(node)
self.addToHead(node)
def removeTail(self):
node = self.tail.prev
self.removeNode(node)
return node
sol = LRUCache(2)
sol.put(1, 1)
res = sol.get(1)
print('==res:', res)
class Solution:
def longestConsecutive(self, nums):
longest_length = 0
num_set = set(nums)#set 比list 快几十倍
print('==num_set:', num_set)
temp = 1
for num in num_set:
if num - 1 in num_set:#如果有小于的就跳过
continue
else:
while num+1 in num_set:#如果有大于的就一直不停更新+1 寻找长度
temp += 1
num += 1
longest_length = max(longest_length, temp)
temp = 1#寻找完结束以后 在初始化为1
print('==longest_length:', longest_length)
return longest_length
nums = [100,4,200,1,3,2,2]
sol = Solution()
sol.longestConsecutive(nums)
class Solution:
def firstUniqChar(self, s):
letter_num = {}
for i in s:
letter_num[i] = letter_num.get(i, 0) + 1
print('==letter_num:', letter_num)
for i in range(len(s)):
if letter_num.get(s[i]) == 1:
return i
print('==res:', res)
return -1
s = "loveleetcode"
# s = ""
# s = "cc"
sol = Solution()
sol.firstUniqChar(s)
class Solution:
def candy(self, ratings):
n = len(ratings)
dp = [0] * n
dp[0] = 1
#每个孩子至少一颗糖 从左往右 找递增的
for i in range(1, n):
if ratings[i] > ratings[i - 1]:
dp[i] = dp[i - 1] + 1
else:
dp[i] = 1
print('==dp:', dp)
#在从右往左 找递增的
for i in range(n - 2, -1, -1):
if ratings[i] > ratings[i + 1] and dp[i] <= dp[i+1]:#i的分比i+1高,同时i的糖还<=i+1的糖
dp[i] = dp[i+1] + 1
print('==dp:', dp)
return sum(dp)
ratings = [1, 0, 2]
# ratings = [1, 3, 4, 5, 2]
sol = Solution()
sol.candy(ratings)