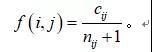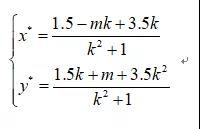数学模型 | 吃鸡游戏中航线蕴含的Winner原理

问题背景
这一天，数小魔又迫不及待地点开“绝地求生·刺激战场”，期望和队友来一场华丽丽的吃鸡秀~~~
……可是，刚落地没多久，身边的人就一平底锅砸了下来，只见屏幕上天旋地转，小魔也就只能无奈地看着队友逍遥快活了…
他决定利用自己学过的数学建模知识，来帮助自己逃脱落地成盒的制裁。

问题重述

  游戏开始时，飞机会随机生成一条直线飞行路径，玩家需要在指定时间内跳伞，并有一段空中调整的时间来接近自己的目的地。请你建立一个数学模型，帮助数小魔解决以下问题：

（1）找出一块降落区域，使得这块地区相对来说物资丰富，且降落人数较少。
（2）对于不同的飞行路线，找出最优的降落方案，使数小魔能够以最快时间到达上一问所选区域的中心。

模型假设
1.不考虑数小魔的操作水平和气流阻力的影响，即给出的降落方案只有重力和降落伞阻力两种外力作用。
2.假设物资水平随着城市密度均匀分布。
3.不考虑“毒圈”的存在对数小魔的决策影响,即各个区域对于数小魔而言是平等的。
4.假设一到目的地就能立即降落。

符号说明
（i，j） 第i行第j列所代表的区域
Cij 区域(i,j)内城市的密度
ni 区域(i,j)内降落的人数
V 飞机飞行的速度
Vf 空中调整状态下的速度
问题分析
（1）本题是一个评估问题+最优化问题。首先根据决策目标给出合理的估价函数，并用其对地图上的各个区域进行评估，使得决策最优化。
（2）本题是一个机理分析问题。首先解决给定航线的情况下跳伞的最佳时机问题，再考虑空中跳伞过程中降落伞的姿态，得到一个航线与最佳跳伞时间的函数关系式。

问题一 · 模型建立与求解

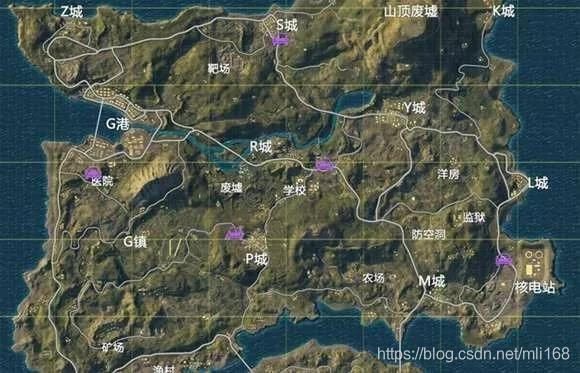
  首先，按照地图上标注的经纬网为地图划分区域，可大致分为5行8列。按照从上至下、从左至右的关系将第i行第j列所代表的区域称为（i,j）。
 分析题意可知，人数越少，物资越丰富，数小魔降落的意愿越高。若定义为城市密度，为区域降落人数，则估价函数可简单定义为：

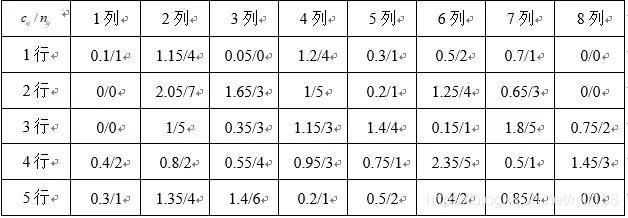
  对地图进行分析，可以很快地确定的数值。采用蒙特卡罗加权随机模拟生成100人的跳伞数据。所得结果如下表所示：

根据估价函数画出热图如下：

图1 估价函数的热图
注意图中的初始标号为0。从图中直接可以看出，区域（2，3）是最理想的降落点。

问题二 · 模型建立与求解

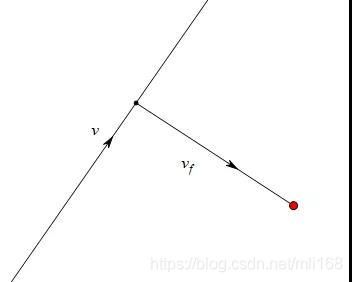
 以地图左下角为原点，一小格边长为单位长，建立平面直角坐标系。则目标区域的中心坐标为 (1.5,3.5)。降落过程示意图如图所示，其中v代表飞机速度,vf代表降落过程中的速度。

图2 降落过程示意图
令飞机的直线方程为y=kx+m，不妨限定k∈[1,3],m∈[0,2]，并假设飞机总是由屏幕最左边飞入。由平面解析几何知识，空中调整的距离为：

图中标出的降落位置为两直线的交点：

由此可算得降落时间为：

即飞机的行进路程为

由此可算得降落时间为：

当给定v=vf=1时，作出t关于k,m的函数图像：

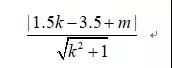
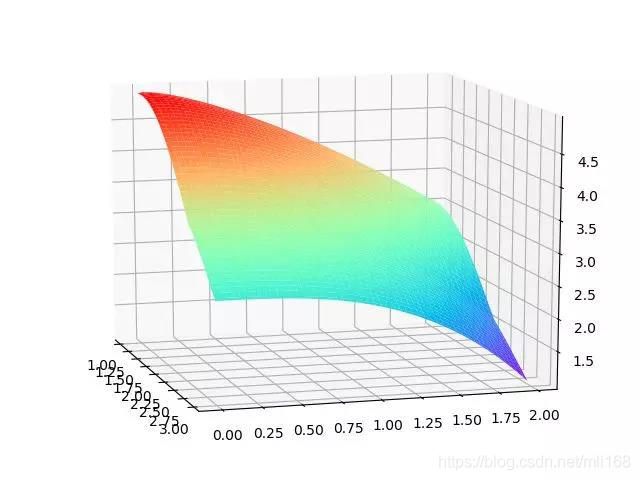
图3 时间关于飞机航线的函数图像

模型结论

   通过问题1的模型，我们得出数小魔降落在区域(2,3)最优的结论。
   观察问题2的三维图像可知，在一定范围内， k越大，m越大，降落时间越短。这有利于帮助数小魔判断降落时的安全状态。

模型评价
模型优点：评估方式合理，对游戏的进行（尤其是对于数小魔这种小菜鸟嘤嘤嘤）具有良好的推动作用，也有利于帮助数小魔在前期得到最好状态，实战作用大。
模型缺点：事实上，我们并不能得知每场比赛中降落人数、飞机速度和降落速度的精确数值，因此我们所做的仅供参考，得到的数据只是定性分析，并不完全精确。

参考文献（略）

附录：Python程序源码

程序1 随机模拟算法
#coding=utf-8
from random import randint
L=[[0 for _ in range(8)] for _ in range(5)]
#篇幅有限，只能放蒙特卡罗的代码段，加权过程略
for i in range(100):
x=randint(0,39)
L[x // 8][x % 8]=L[x // 8][x % 8]+1
for i in range(5):
print(L[i])
程序2 热图绘制
#coding=utf-8
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
L=[
[0.1/2,1.15/5,0.05/1,1.2/5,0.3/2,0.5/3,0.7/2,0],
[0,2.05/8,1.65/4,1/6,0.2/2,1.25/5,0.65/4,0],
[0,1/6,0.35/4,1.15/4,1.4/5,0.15/2,1.8/6,0.75/3],
[0.4/3,0.8/3,0.55/5,0.95/4,0.75/2,2.35/6,0.5/2,1.45/4],
[0.3/2,1.35/5,1.4/7,0.2/2,0.5/3,0.4/3,0.85/5,0]
]
sns.set(style=‘whitegrid’, color_codes=True)
H=np.array(L)
ax=sns.heatmap(L)
plt.show()
程序3 3D图像绘制
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
figure=plt.figure()
ax=Axes3D(figure)
k=np.arange(1,3,.02)
m=np.arange(0,2,.02)
k,m=np.meshgrid(k,m)
t=abs(1.5k-3.5)/np.sqrt(k**k+1)+(1.5+3.5k-mk)/np.sqrt(kk+1)
ax.plot_surface(k,m,t,cmap=‘rainbow’)
plt.show()

来源：山东大学
文案 / 陈诺
编辑 / 杨汉
责任编辑 / 崔雨濛