LeetCode算法:900~1576道
目录
912. 排序数组
918. 环形子数组的最大和
922. 按奇偶排序数组 II
929. 独特的电子邮件地址
930. 和相同的二元子数组
931. 下降路径最小和
933. 最近的请求次数
938. 二叉搜索树的范围和
946. 验证栈序列
952. 按公因数计算最大组件大小
955. 删列造序 II
958. 二叉树的完全性检验
961. 重复 N 次的元素
973. 最接近原点的 K 个点
977. 有序数组的平方
978. 最长湍流子数组
987. 二叉树的垂序遍历
989. 数组形式的整数加法
999. 车的可用捕获量
1004. 最大连续 1 的个数 III
1008. 先序遍历构造二叉树
1009. 十进制整数的反码
1010. 总持续时间可被 60 整除的歌曲
1017. 负二进制转换
1019. 链表中的下一个更大节点
1021. 删除最外层的括号
1022. 从根到叶的二进制数之和
1025. 除数博弈
1026. 节点与其祖先之间的最大差值
1029. 两地调度
1030. 距离顺序排列矩阵单元格
1033. 移动石子直到连续
1034. 边框着色
1036. 逃离大迷宫
1037. 有效的回旋镖
1038. 从二叉搜索树到更大和树
1041. 困于环中的机器人
1043. 分隔数组以得到最大和
1046. 最后一块石头的重量
1047. 删除字符串中的所有相邻重复项
1048. 最长字符串链
1051. 高度检查器
1052. 爱生气的书店老板
1053. 交换一次的先前排列
1054. 距离相等的条形码
1071. 字符串的最大公因子
1072. 按列翻转得到最大值等行数
1073. 负二进制数相加
1074. 元素和为目标值的子矩阵数量
1079. 活字印刷
1080. 根到叶路径上的不足节点
1081. 不同字符的最小子序列
1089. 复写零
1090. 受标签影响的最大值
1091. 二进制矩阵中的最短路径
1093. 大样本统计
1094. 拼车
1095. 山脉数组中查找目标值
1103. 分糖果 II
1104. 二叉树寻路
1108. IP 地址无效化
1109. 航班预订统计
1110. 删点成林
1111. 有效括号的嵌套深度
1114. 按序打印
1115. 交替打印 FooBar
1116. 打印零与奇偶数
1117. H2O 生成
1122. 数组的相对排序
1123. 最深叶节点的最近公共祖先
1124. 表现良好的最长时间段
1128. 等价多米诺骨牌对的数量
1137. 第 N 个泰波那契数
1138. 字母板上的路径
1139. 最大的以 1 为边界的正方形
1140. 石子游戏 II
1144. 递减元素使数组呈锯齿状
1147. 段式回文
1155. 掷骰子的 N 种方法
1171. 从链表中删去总和值为零的连续节点
1184. 公交站间的距离
1185. 一周中的第几天
1195. 交替打印字符串
1287. 有序数组中出现次数超过 25%的元素
1290. 二进制链表转整数
1295. 统计位数为偶数的数字
1346. 检查整数及其两倍数是否存在
1347. 制造字母异位词的最小步骤数
1380. 矩阵中的幸运数
1476. 子矩形查询
1535. 找出数组游戏的赢家
1537. 最大得分
1541. 平衡括号字符串的最少插入次数
1544. 整理字符串
1545. 找出第 N 个二进制字符串中的第 K 位
1546. 和为目标值的最大数目不重叠非空子数组数目
1550. 存在连续三个奇数的数组
1551. 使数组中所有元素相等的最小操作数
1552. 两球之间的磁力
1553. 吃掉 N 个橘子的最少天数
1560. 圆形赛道上经过次数最多的扇区
1561. 你可以获得的最大硬币数目
1562. 查找大小为 M 的最新分组
1566. 重复至少 K 次且长度为 M 的模式
1567. 乘积为正数的最长子数组长度
1569. 将子数组重新排序得到同一个二叉查找树的方案数
1572. 矩阵对角线元素的和
1573. 分割字符串的方案数
1574. 删除最短的子数组使剩余数组有序
1576. 替换所有的问号
912. 排序数组
English Version
题目描述
给定一个整数数组 nums,将该数组升序排列。
示例 1:
输入:[5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:[5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= A.length <= 10000-50000 <= A[i] <= 50000
解法
Python3
Java
class Solution {
void createHeap(int[] data, int n, int h) {
int i = h;
int j = 2 * i + 1;
int temp = data[i];
while (j < n) {
if (j + 1 < n && data[j] < data[j + 1]) j++;
if (temp > data[j]) {
break;
} else {
data[i] = data[j];
i = j;
j = 2 * i + 1;
}
}
data[i] = temp;
}
void initHeap(int[] data, int n) {
for (int i = (n - 2) / 2; i > -1; i--) {
createHeap(data, n, i);
}
}
void heapSort(int[] data, int n) {
initHeap(data, n);
for (int i = n - 1;i > -1;i--) {
int temp = data[i];
data[i] = data[0];
data[0] = temp;
createHeap(data, i, 0);
}
}
public int[] sortArray(int[] nums) {
heapSort(nums, nums.length);
return nums;
}
}
…
918. 环形子数组的最大和
English Version
题目描述
给定一个由整数数组 A 表示的环形数组 C,求 C 的非空子数组的最大可能和。
在此处,环形数组意味着数组的末端将会与开头相连呈环状。(形式上,当0 <= i < A.length 时 C[i] = A[i],而当 i >= 0 时 C[i+A.length] = C[i])
此外,子数组最多只能包含固定缓冲区 A 中的每个元素一次。(形式上,对于子数组 C[i], C[i+1], ..., C[j],不存在 i <= k1, k2 <= j 其中 k1 % A.length = k2 % A.length)
示例 1:
输入:[1,-2,3,-2] 输出:3 解释:从子数组 [3] 得到最大和 3
示例 2:
输入:[5,-3,5] 输出:10 解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:[3,-1,2,-1] 输出:4 解释:从子数组 [2,-1,3] 得到最大和 2 + (-1) + 3 = 4
示例 4:
输入:[3,-2,2,-3] 输出:3 解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
示例 5:
输入:[-2,-3,-1] 输出:-1 解释:从子数组 [-1] 得到最大和 -1
提示:
-30000 <= A[i] <= 300001 <= A.length <= 30000
解法
Python3
Java
class Solution {
public int maxSubarraySumCircular(int[] A) {
int tot = 0;
int curMax = 0;
int maxSum = Integer.MIN_VALUE;
int curMin = 0;
int minSum = Integer.MAX_VALUE;
for (int x : A) {
tot += x;
curMax = Math.max(curMax + x, x);
maxSum = Math.max(maxSum, curMax);
curMin = Math.min(curMin + x, x);
minSum = Math.min(minSum, curMin);
}
return maxSum > 0 ? Math.max(maxSum, tot - minSum) : maxSum;
}
}
…
922. 按奇偶排序数组 II
English Version
题目描述
给定一个非负整数数组 A, A 中一半整数是奇数,一半整数是偶数。
对数组进行排序,以便当 A[i] 为奇数时,i 也是奇数;当 A[i] 为偶数时, i 也是偶数。
你可以返回任何满足上述条件的数组作为答案。
示例:
输入:[4,2,5,7] 输出:[4,5,2,7] 解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。
提示:
2 <= A.length <= 20000A.length % 2 == 00 <= A[i] <= 1000
解法
Python3
Java
class Solution {
public int[] sortArrayByParityII(int[] A) {
int j = 1, length = A.length;
for (int i = 0; i < length; i += 2) {
if ((A[i] & 1) != 0) {
while ((A[j] & 1) != 0) j += 2;
// Swap A[i] and A[j]
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
}
return A;
}
}
…
929. 独特的电子邮件地址
English Version
题目描述
每封电子邮件都由一个本地名称和一个域名组成,以 @ 符号分隔。
例如,在 [email protected]中, alice 是本地名称,而 leetcode.com 是域名。
除了小写字母,这些电子邮件还可能包含 '.' 或 '+'。
如果在电子邮件地址的本地名称部分中的某些字符之间添加句点('.'),则发往那里的邮件将会转发到本地名称中没有点的同一地址。例如,"[email protected]” 和 “[email protected]” 会转发到同一电子邮件地址。 (请注意,此规则不适用于域名。)
如果在本地名称中添加加号('+'),则会忽略第一个加号后面的所有内容。这允许过滤某些电子邮件,例如 [email protected] 将转发到 [email protected]。 (同样,此规则不适用于域名。)
可以同时使用这两个规则。
给定电子邮件列表 emails,我们会向列表中的每个地址发送一封电子邮件。实际收到邮件的不同地址有多少?
示例:
输入:["[email protected]","[email protected]","[email protected]"] 输出:2 解释:实际收到邮件的是 "[email protected]" 和 "[email protected]"。
提示:
1 <= emails[i].length <= 1001 <= emails.length <= 100- 每封
emails[i]都包含有且仅有一个'@'字符。
解法
Python3
Java
class Solution {
public int numUniqueEmails(String[] emails) {
Set<String> set = new HashSet<>();
for (String email : emails) {
int index = email.indexOf('@');
String local = email.substring(0, index);
String domain = email.substring(index);
index = local.indexOf('+');
if (index != -1) {
local = local.substring(0, index);
}
local = local.replace(".", "");
set.add(local + domain);
}
return set.size();
}
}
…
930. 和相同的二元子数组
English Version
题目描述
在由若干 0 和 1 组成的数组 A 中,有多少个和为 S 的非空子数组。
示例:
输入:A = [1,0,1,0,1], S = 2 输出:4 解释: 如下面黑体所示,有 4 个满足题目要求的子数组: [1,0,1,0,1] [1,0,1,0,1] [1,0,1,0,1] [1,0,1,0,1]
提示:
A.length <= 300000 <= S <= A.lengthA[i]为0或1
解法
Python3
Java
class Solution {
public int numSubarraysWithSum(int[] A, int S) {
int[] map = new int[A.length + 1];
map[0] = 1;
int res = 0;
int s = 0;
for (int a : A) {
s += a;
if (s >= S) {
res += map[s - S];
}
++map[s];
}
return res;
}
}
…
931. 下降路径最小和
English Version
题目描述
给定一个方形整数数组 A,我们想要得到通过 A 的下降路径的最小和。
下降路径可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列。
示例:
输入:[[1,2,3],[4,5,6],[7,8,9]] 输出:12 解释: 可能的下降路径有:
[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9][2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9][3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]
和最小的下降路径是 [1,4,7],所以答案是 12。
提示:
1 <= A.length == A[0].length <= 100-100 <= A[i][j] <= 100
解法
Python3
Java
class Solution {
public int minFallingPathSum(int[][] A) {
int m = A.length, n = A[0].length;
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int min = A[i - 1][j];
if (j > 0) min = Math.min(min, A[i - 1][j - 1]);
if (j < n - 1) min = Math.min(min, A[i - 1][j + 1]);
A[i][j] += min;
}
}
return Arrays.stream(A[m - 1]).min().getAsInt();
}
}
…
933. 最近的请求次数
English Version
题目描述
写一个 RecentCounter 类来计算最近的请求。
它只有一个方法:ping(int t),其中 t 代表以毫秒为单位的某个时间。
返回从 3000 毫秒前到现在的 ping 数。
任何处于 [t - 3000, t] 时间范围之内的 ping 都将会被计算在内,包括当前(指 t 时刻)的 ping。
保证每次对 ping 的调用都使用比之前更大的 t 值。
示例:
输入:inputs = ["RecentCounter","ping","ping","ping","ping"], inputs = [[],[1],[100],[3001],[3002]] 输出:[null,1,2,3,3]
提示:
- 每个测试用例最多调用
10000次ping。 - 每个测试用例会使用严格递增的
t值来调用ping。 - 每次调用
ping都有1 <= t <= 10^9。
解法
在第 1、100、3001、3002 这四个时间点分别进行了 ping 请求, 在 3001 秒的时候, 它前面的 3000 秒指的是区间 [1,3001], 所以一共是有 1、100、3001 三个请求, t = 3002 的前 3000 秒指的是区间 [2,3002], 所以有 100、3001、3002 三次请求。
可以用队列实现。每次将 t 进入队尾,同时从队头开始依次移除小于 t-3000 的元素。然后返回队列的大小 q.size() 即可。
Python3
class RecentCounter:
def __init__(self):
self.q = []
def ping(self, t: int) -> int:
self.q.append(t)
while self.q[0] < t - 3000:
self.q.pop(0)
return len(self.q)
# Your RecentCounter object will be instantiated and called as such:
# obj = RecentCounter()
# param_1 = obj.ping(t)
Java
class RecentCounter {
private Deque<Integer> q;
public RecentCounter() {
q = new ArrayDeque<>();
}
public int ping(int t) {
q.offerLast(t);
while (q.peekFirst() < t - 3000) {
q.pollFirst();
}
return q.size();
}
}
/**
* Your RecentCounter object will be instantiated and called as such:
* RecentCounter obj = new RecentCounter();
* int param_1 = obj.ping(t);
*/
…
938. 二叉搜索树的范围和
English Version
题目描述
给定二叉搜索树的根结点 root,返回 L 和 R(含)之间的所有结点的值的和。
二叉搜索树保证具有唯一的值。
示例 1:
输入:root = [10,5,15,3,7,null,18], L = 7, R = 15 输出:32
示例 2:
输入:root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10 输出:23
提示:
- 树中的结点数量最多为
10000个。 - 最终的答案保证小于
2^31。
解法
Python3
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int res = 0;
public int rangeSumBST(TreeNode root, int L, int R) {
if (root == null) {
return res;
}
if (root.val < L) {
rangeSumBST(root.right, L, R);
} else if (root.val > R) {
rangeSumBST(root.left, L, R);
} else {
res += root.val;
rangeSumBST(root.left, L, R);
rangeSumBST(root.right, L, R);
}
return res;
}
}
…
946. 验证栈序列
English Version
题目描述
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1] 输出:true 解释:我们可以按以下顺序执行: push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2] 输出:false 解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed是popped的排列。
解法
Python3
Java
import java.util.*;
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
int i = 0, k = 0;
while (i < popped.length) {
if (!stack.isEmpty() && popped[i] == stack.peek()) {
stack.pop();
i ++;
} else {
if (k < pushed.length) {
stack.push(pushed[k ++]);
} else return false;
}
}
return stack.isEmpty();
}
}
…
952. 按公因数计算最大组件大小
English Version
题目描述
给定一个由不同正整数的组成的非空数组 A,考虑下面的图:
- 有
A.length个节点,按从A[0]到A[A.length - 1]标记; - 只有当
A[i]和A[j]共用一个大于 1 的公因数时,A[i]和A[j]之间才有一条边。
返回图中最大连通组件的大小。
示例 1:
输入:[4,6,15,35] 输出:4
示例 2:
输入:[20,50,9,63] 输出:2
示例 3:
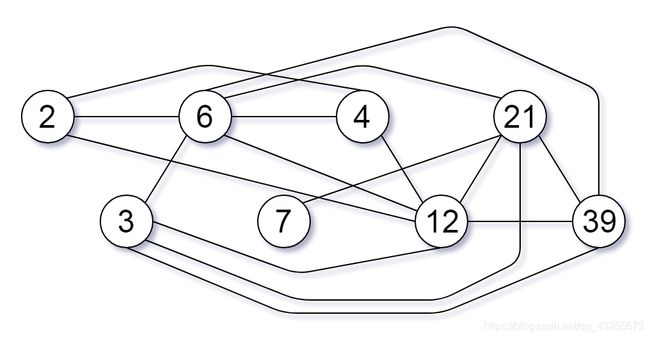
输入:[2,3,6,7,4,12,21,39] 输出:8
提示:
1 <= A.length <= 200001 <= A[i] <= 100000
解法
Python3
Java
class Solution {
public int largestComponentSize(int[] A) {
int n = A.length, num = 100000 + 1, max = 0;
Set<Integer> primes = findPrime(num);
int[] root = new int[n];
int[] size = new int[n];
int[] primeToNode = new int[num];
// 一开始 prime 没有和数组 A 中的 node 连在一起
Arrays.fill(primeToNode, -1);
// 初始化 root 和 size array
for (int i = 0; i < n; i++) {
root[i] = i;
size[i] = 1;
}
for (int i = 0; i < n; i++) {
int curr = A[i];
// find all of its prime factors
for (Integer prime: primes) {
if (primes.contains(curr)) {
prime = curr;
}
if (curr % prime == 0) {
// 我们为 curr 找到一个质因数,则需要将该节点加入该 prime 已经连接到的根节点上
if (primeToNode[prime] != -1) {
// 该 prime 已经与数组 A 中 node 相连
union(size, root, primeToNode[prime], i);
}
primeToNode[prime] = find(root, i);
while (curr % prime == 0) {
// 将质因数 prime 全部剔除
curr = curr / prime;
}
}
if (curr == 1) {
break;
}
}
}
for (int i = 0; i < n; i++) {
max = Math.max(size[i], max);
}
return max;
}
public Set<Integer> findPrime(int num) {
boolean[] isPrime = new boolean[num];
Arrays.fill(isPrime, true);
Set<Integer> primes = new HashSet<>();
for (int i = 2; i < isPrime.length; i++) {
if (isPrime[i]) {
primes.add(i);
for (int j = 0; i * j < isPrime.length; j++) {
isPrime[i * j] = false;
}
}
}
return primes;
}
public void union(int[] size, int[] root, int i, int j) {
int rootI = find(root, i);
int rootJ = find(root, j);
if (rootI == rootJ) {
// 它们已经属于同一个 root
return;
}
if (size[rootI] > size[rootJ]) {
root[rootJ] = rootI;
size[rootI] += size[rootJ];
} else {
root[rootI] = rootJ;
size[rootJ] += size[rootI];
}
}
public int find(int[] root, int i) {
// 当某节点的根不是他自己时,则需要继续找到其 root
List<Integer> records = new LinkedList<>();
while (root[i] != i) {
records.add(i);
i = root[i];
}
// 将这些节点均指向其 root
for (Integer record: records) {
root[record] = i;
}
return i;
}
}
…
955. 删列造序 II
English Version
题目描述
给定由 N 个小写字母字符串组成的数组 A,其中每个字符串长度相等。
选取一个删除索引序列,对于 A 中的每个字符串,删除对应每个索引处的字符。
比如,有 A = ["abcdef", "uvwxyz"],删除索引序列 {0, 2, 3},删除后 A 为["bef", "vyz"]。
假设,我们选择了一组删除索引 D,那么在执行删除操作之后,最终得到的数组的元素是按 字典序(A[0] <= A[1] <= A[2] ... <= A[A.length - 1])排列的,然后请你返回 D.length 的最小可能值。
示例 1:
输入:["ca","bb","ac"] 输出:1 解释: 删除第一列后,A = ["a", "b", "c"]。 现在 A 中元素是按字典排列的 (即,A[0] <= A[1] <= A[2])。 我们至少需要进行 1 次删除,因为最初 A 不是按字典序排列的,所以答案是 1。
示例 2:
输入:["xc","yb","za"] 输出:0 解释: A 的列已经是按字典序排列了,所以我们不需要删除任何东西。 注意 A 的行不需要按字典序排列。 也就是说,A[0][0] <= A[0][1] <= ... 不一定成立。
示例 3:
输入:["zyx","wvu","tsr"] 输出:3 解释: 我们必须删掉每一列。
提示:
1 <= A.length <= 1001 <= A[i].length <= 100
解法
Python3
Java
class Solution {
public int minDeletionSize(String[] A) {
if (A == null || A.length <= 1) {
return 0;
}
int len = A.length, wordLen = A[0].length(), res = 0;
boolean[] cut = new boolean[len];
search: for (int j = 0; j < wordLen; j++) {
// 判断第 j 列是否应当保留
for (int i = 0; i < len - 1; i++) {
if (!cut[i] && A[i].charAt(j) > A[i + 1].charAt(j)) {
res += 1;
continue search;
}
}
// 更新 cut 的信息
for (int i = 0; i < len - 1; i++) {
if (A[i].charAt(j) < A[i + 1].charAt(j)) {
cut[i] = true;
}
}
}
return res;
}
}
…
958. 二叉树的完全性检验
English Version
题目描述
给定一个二叉树,确定它是否是一个完全二叉树。
百度百科中对完全二叉树的定义如下:
若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。(注:第 h 层可能包含 1~ 2h 个节点。)
示例 1:
输入:[1,2,3,4,5,6]
输出:true
解释:最后一层前的每一层都是满的(即,结点值为 {1} 和 {2,3} 的两层),且最后一层中的所有结点({4,5,6})都尽可能地向左。
示例 2:
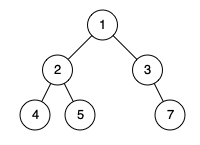输入:[1,2,3,4,5,null,7] 输出:false 解释:值为 7 的结点没有尽可能靠向左侧。
提示:
- 树中将会有 1 到 100 个结点。
解法
Python3
Java
class Solution {
public boolean isCompleteTree(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (queue.peek() != null) {
TreeNode node = queue.poll();
queue.offer(node.left);
queue.offer(node.right);
}
while (!queue.isEmpty() && queue.peek() == null) {
queue.poll();
}
return queue.isEmpty();
}
}
…
961. 重复 N 次的元素
English Version
题目描述
在大小为 2N 的数组 A 中有 N+1 个不同的元素,其中有一个元素重复了 N 次。
返回重复了 N 次的那个元素。
示例 1:
输入:[1,2,3,3] 输出:3
示例 2:
输入:[2,1,2,5,3,2] 输出:2
示例 3:
输入:[5,1,5,2,5,3,5,4] 输出:5
提示:
4 <= A.length <= 100000 <= A[i] < 10000A.length为偶数
解法
Python3
Java
class Solution {
public int repeatedNTimes(int[] A) {
Set<Integer> set = new HashSet<>();
for (int e : A) {
if (set.contains(e)) {
return e;
}
set.add(e);
}
return 0;
}
}
…
973. 最接近原点的 K 个点
English Version
题目描述
我们有一个由平面上的点组成的列表 points。需要从中找出 K 个距离原点 (0, 0) 最近的点。
(这里,平面上两点之间的距离是欧几里德距离。)
你可以按任何顺序返回答案。除了点坐标的顺序之外,答案确保是唯一的。
示例 1:
输入:points = [[1,3],[-2,2]], K = 1 输出:[[-2,2]] 解释: (1, 3) 和原点之间的距离为 sqrt(10), (-2, 2) 和原点之间的距离为 sqrt(8), 由于 sqrt(8) < sqrt(10),(-2, 2) 离原点更近。 我们只需要距离原点最近的 K = 1 个点,所以答案就是 [[-2,2]]。
示例 2:
输入:points = [[3,3],[5,-1],[-2,4]], K = 2 输出:[[3,3],[-2,4]] (答案 [[-2,4],[3,3]] 也会被接受。)
提示:
1 <= K <= points.length <= 10000-10000 < points[i][0] < 10000-10000 < points[i][1] < 10000
解法
Python3
Java
import java.util.*;
/**
* @author Furaha Damien
*/
class Solution {
// Helper inner class
public class Point {
int x;
int y;
int distance;
public Point(int x, int y, int distance) {
this.x = x;
this.y = y;
this.distance = distance;
}
}
public int[][] kClosest(int[][] points, int K) {
PriorityQueue<Point> que = new PriorityQueue<Point>((a, b) -> (a.distance - b.distance));
int[][] res = new int[K][2];
for (int[] temp : points) {
int dist = (temp[0] * temp[0] + temp[1] * temp[1]);
que.offer(new Point(temp[0], temp[1], dist));
}
for (int i = 0; i < K; i++) {
Point curr = que.poll();
res[i][0] = curr.x;
res[i][1] = curr.y;
}
return res;
}
}
…
977. 有序数组的平方
English Version
题目描述
给定一个按非递减顺序排序的整数数组 A,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。
示例 1:
输入:[-4,-1,0,3,10] 输出:[0,1,9,16,100]
示例 2:
输入:[-7,-3,2,3,11] 输出:[4,9,9,49,121]
提示:
1 <= A.length <= 10000-10000 <= A[i] <= 10000A已按非递减顺序排序。
解法
Python3
Java
class Solution {
public int[] sortedSquares(int[] A) {
for (int i = 0, n = A.length; i < n; ++i) {
A[i] = A[i] * A[i];
}
Arrays.sort(A);
return A;
}
}
…
978. 最长湍流子数组
English Version
题目描述
当 A 的子数组 A[i], A[i+1], ..., A[j] 满足下列条件时,我们称其为湍流子数组:
- 若
i <= k < j,当k为奇数时,A[k] > A[k+1],且当k为偶数时,A[k] < A[k+1]; - 或 若
i <= k < j,当k为偶数时,A[k] > A[k+1],且当k为奇数时,A[k] < A[k+1]。
也就是说,如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是湍流子数组。
返回 A 的最大湍流子数组的长度。
示例 1:
输入:[9,4,2,10,7,8,8,1,9] 输出:5 解释:(A[1] > A[2] < A[3] > A[4] < A[5])
示例 2:
输入:[4,8,12,16] 输出:2
示例 3:
输入:[100] 输出:1
提示:
1 <= A.length <= 400000 <= A[i] <= 10^9
解法
Python3
Java
class Solution {
public int maxTurbulenceSize(int[] A) {
int res = 1;
int up = 1, down = 1;
for (int i = 1; i < A.length; ++i) {
if (A[i] > A[i - 1]) {
up = down + 1;
down = 1;
res = Math.max(res, up);
} else if (A[i] < A[i - 1]) {
down = up + 1;
up = 1;
res = Math.max(res, down);
} else {
up = 1;
down = 1;
}
}
return res;
}
}
…
987. 二叉树的垂序遍历
English Version
题目描述
给定二叉树,按垂序遍历返回其结点值。
对位于 (X, Y) 的每个结点而言,其左右子结点分别位于 (X-1, Y-1) 和 (X+1, Y-1)。
把一条垂线从 X = -infinity 移动到 X = +infinity ,每当该垂线与结点接触时,我们按从上到下的顺序报告结点的值( Y 坐标递减)。
如果两个结点位置相同,则首先报告的结点值较小。
按 X 坐标顺序返回非空报告的列表。每个报告都有一个结点值列表。
示例 1:
输入:[3,9,20,null,null,15,7] 输出:[[9],[3,15],[20],[7]] 解释: 在不丧失其普遍性的情况下,我们可以假设根结点位于 (0, 0): 然后,值为 9 的结点出现在 (-1, -1); 值为 3 和 15 的两个结点分别出现在 (0, 0) 和 (0, -2); 值为 20 的结点出现在 (1, -1); 值为 7 的结点出现在 (2, -2)。
示例 2:
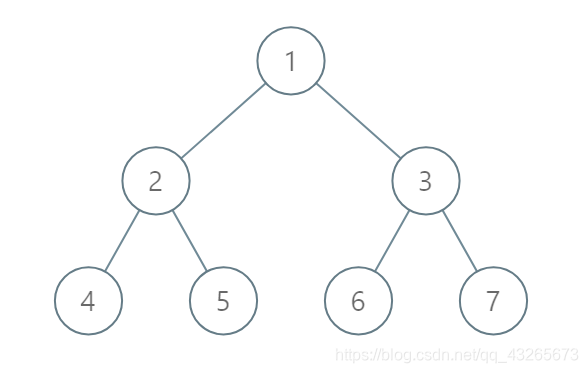输入:[1,2,3,4,5,6,7] 输出:[[4],[2],[1,5,6],[3],[7]] 解释: 根据给定的方案,值为 5 和 6 的两个结点出现在同一位置。 然而,在报告 "[1,5,6]" 中,结点值 5 排在前面,因为 5 小于 6。
提示:
- 树的结点数介于
1和1000之间。 - 每个结点值介于
0和1000之间。
解法
Python3
Java
class Solution {
public List<List<Integer>> verticalTraversal(TreeNode root) {
List<int[]> list = new ArrayList<>();
dfs(root, 0, 0, list);
list.sort(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if (o1[0] != o2[0]) return Integer.compare(o1[0], o2[0]);
if (o1[1] != o2[1]) return Integer.compare(o2[1], o1[1]);
return Integer.compare(o1[2], o2[2]);
}
});
List<List<Integer>> res = new ArrayList<>();
int preX = 1;
for (int[] cur : list) {
if (preX != cur[0]) {
res.add(new ArrayList<>());
preX = cur[0];
}
res.get(res.size() - 1).add(cur[2]);
}
return res;
}
private void dfs(TreeNode root, int x, int y, List<int[]> list) {
if (root == null) {
return;
}
list.add(new int[]{
x, y, root.val});
dfs(root.left, x - 1, y - 1, list);
dfs(root.right, x + 1, y - 1, list);
}
}
…
989. 数组形式的整数加法
English Version
题目描述
对于非负整数 X 而言,X 的数组形式是每位数字按从左到右的顺序形成的数组。例如,如果 X = 1231,那么其数组形式为 [1,2,3,1]。
给定非负整数 X 的数组形式 A,返回整数 X+K 的数组形式。
示例 1:
输入:A = [1,2,0,0], K = 34 输出:[1,2,3,4] 解释:1200 + 34 = 1234
示例 2:
输入:A = [2,7,4], K = 181 输出:[4,5,5] 解释:274 + 181 = 455
示例 3:
输入:A = [2,1,5], K = 806 输出:[1,0,2,1] 解释:215 + 806 = 1021
示例 4:
输入:A = [9,9,9,9,9,9,9,9,9,9], K = 1 输出:[1,0,0,0,0,0,0,0,0,0,0] 解释:9999999999 + 1 = 10000000000
提示:
1 <= A.length <= 100000 <= A[i] <= 90 <= K <= 10000- 如果
A.length > 1,那么A[0] != 0
解法
Python3
Java
class Solution {
public List<Integer> addToArrayForm(int[] A, int K) {
for (int i = A.length - 1; i >= 0 && K != 0; --i) {
K += A[i];
A[i] = K % 10;
K /= 10;
}
List<Integer> res = new ArrayList<>();
while (K != 0) {
res.add(K % 10);
K /= 10;
}
Collections.reverse(res);
for (int a : A) {
res.add(a);
}
return res;
}
}
…
999. 车的可用捕获量
English Version
题目描述
在一个 8 x 8 的棋盘上,有一个白色车(rook)。也可能有空方块,白色的象(bishop)和黑色的卒(pawn)。它们分别以字符 “R”,“.”,“B” 和 “p” 给出。大写字符表示白棋,小写字符表示黑棋。
车按国际象棋中的规则移动:它选择四个基本方向中的一个(北,东,西和南),然后朝那个方向移动,直到它选择停止、到达棋盘的边缘或移动到同一方格来捕获该方格上颜色相反的卒。另外,车不能与其他友方(白色)象进入同一个方格。
返回车能够在一次移动中捕获到的卒的数量。
示例 1:
输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]] 输出:3 解释: 在本例中,车能够捕获所有的卒。
示例 2:
输入:[[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]] 输出:0 解释: 象阻止了车捕获任何卒。
示例 3:
输入:[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]] 输出:3 解释: 车可以捕获位置 b5,d6 和 f5 的卒。
提示:
board.length == board[i].length == 8board[i][j]可以是'R','.','B'或'p'- 只有一个格子上存在
board[i][j] == 'R'
解法
先找到 R 的位置,之后向“上、下、左、右”四个方向查找,累加结果。
Python3
class Solution:
def numRookCaptures(self, board: List[List[str]]) -> int:
def search(board, i, j, direction):
while i >= 0 and i < 8 and j >= 0 and j < 8:
if board[i][j] == 'B': return 0
if board[i][j] == 'p': return 1
i += direction[0]
j += direction[1]
return 0
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
res = 0;
for i in range(8):
for j in range(8):
if board[i][j] == 'R':
for direction in directions:
res += search(board, i, j, direction)
return res
Java
class Solution {
public int numRookCaptures(char[][] board) {
int[][] directions = {
{
-1, 0}, {
1, 0}, {
0, -1}, {
0, 1} };
int res = 0;
for (int i = 0; i < 8; ++i) {
for (int j = 0; j < 8; ++j) {
if (board[i][j] == 'R') {
for (int[] direction : directions) {
res += search(board, i, j, direction);
}
return res;
}
}
}
return res;
}
private int search(char[][] board, int i, int j, int[] direction) {
while (i >= 0 && i < 8 && j >= 0 && j < 8) {
if (board[i][j] == 'B') return 0;
if (board[i][j] == 'p') return 1;
i += direction[0];
j += direction[1];
}
return 0;
}
}
…
1004. 最大连续 1 的个数 III
English Version
题目描述
给定一个由若干 0 和 1 组成的数组 A,我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长(连续)子数组的长度。
示例 1:
输入:A = [1,1,1,0,0,0,1,1,1,1,0], K = 2 输出:6 解释: [1,1,1,0,0,1,1,1,1,1,1] 粗体数字从 0 翻转到 1,最长的子数组长度为 6。
示例 2:
输入:A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3 输出:10 解释: [0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1] 粗体数字从 0 翻转到 1,最长的子数组长度为 10。
提示:
1 <= A.length <= 200000 <= K <= A.lengthA[i]为0或1
解法
Python3
Java
class Solution {
public int longestOnes(int[] A, int K) {
int l = 0, r = 0;
while (r < A.length) {
if (A[r++] == 0) --K;
if (K < 0 && A[l++] == 0) ++K;
}
return r - l;
}
}
…
1008. 先序遍历构造二叉树
English Version
题目描述
返回与给定先序遍历 preorder 相匹配的二叉搜索树(binary search tree)的根结点。
(回想一下,二叉搜索树是二叉树的一种,其每个节点都满足以下规则,对于 node.left 的任何后代,值总 < node.val,而 node.right 的任何后代,值总 > node.val。此外,先序遍历首先显示节点的值,然后遍历 node.left,接着遍历 node.right。)
示例:
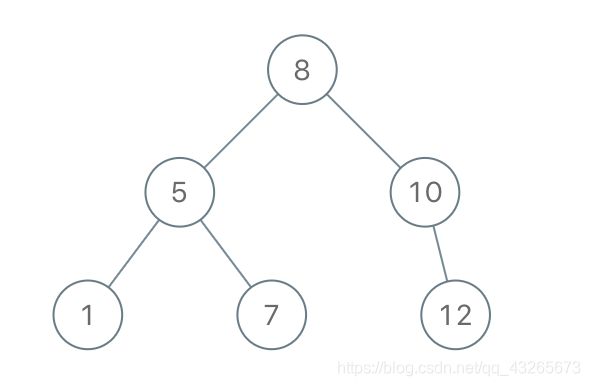
输入:[8,5,1,7,10,12] 输出:[8,5,10,1,7,null,12]
提示:
1 <= preorder.length <= 100- 先序
preorder中的值是不同的。
解法
Python3
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
if (preorder == null || preorder.length == 0) {
return null;
}
// 进入分治法的递归
return helper(preorder, 0, preorder.length - 1);
}
private TreeNode helper(int[] preorder, int start, int end) {
// System.out.println("start: " + start + " end: " + end);
// 确认递归结束的标志,当 start == end 时,表示该区间只剩下一个 subRoot 节点
if (start > end) {
return null;
}
if (start == end) {
return new TreeNode(preorder[start]);
}
// 前序遍历,首先遍历到的为根
TreeNode root = new TreeNode(preorder[start]);
int leftEnd = start;
while (leftEnd <= end) {
if (preorder[leftEnd] > preorder[start]) {
break;
}
leftEnd++;
}
// System.out.println("leftEnd:" + leftEnd + " num: " + preorder[leftEnd]);
root.left = helper(preorder, start + 1, leftEnd - 1);
root.right = helper(preorder, leftEnd, end);
return root;
}
}
…
1009. 十进制整数的反码
English Version
题目描述
每个非负整数 N 都有其二进制表示。例如, 5 可以被表示为二进制 "101",11 可以用二进制 "1011" 表示,依此类推。注意,除 N = 0 外,任何二进制表示中都不含前导零。
二进制的反码表示是将每个 1 改为 0 且每个 0 变为 1。例如,二进制数 "101" 的二进制反码为 "010"。
给你一个十进制数 N,请你返回其二进制表示的反码所对应的十进制整数。
示例 1:
输入:5 输出:2 解释:5 的二进制表示为 "101",其二进制反码为 "010",也就是十进制中的 2 。
示例 2:
输入:7 输出:0 解释:7 的二进制表示为 "111",其二进制反码为 "000",也就是十进制中的 0 。
示例 3:
输入:10 输出:5 解释:10 的二进制表示为 "1010",其二进制反码为 "0101",也就是十进制中的 5 。
提示:
0 <= N < 10^9- 本题与 476:https://leetcode-cn.com/problems/number-complement/ 相同
解法
Python3
Java
class Solution {
public int bitwiseComplement(int N) {
int ans = 0;
int index = -1;
if (N == 0) return 1;
if (N == 1) return 0;
while (N / 2 != 0) {
index++;
int temp = N % 2 == 0 ? 1 : 0;
if (temp == 1) {
ans += Math.pow(2, index);
}
N /= 2;
}
return ans;
}
}
…
1010. 总持续时间可被 60 整除的歌曲
English Version
题目描述
在歌曲列表中,第 i 首歌曲的持续时间为 time[i] 秒。
返回其总持续时间(以秒为单位)可被 60 整除的歌曲对的数量。形式上,我们希望索引的数字 i < j 且有 (time[i] + time[j]) % 60 == 0。
示例 1:
输入:[30,20,150,100,40] 输出:3 解释:这三对的总持续时间可被 60 整数: (time[0] = 30, time[2] = 150): 总持续时间 180 (time[1] = 20, time[3] = 100): 总持续时间 120 (time[1] = 20, time[4] = 40): 总持续时间 60
示例 2:
输入:[60,60,60] 输出:3 解释:所有三对的总持续时间都是 120,可以被 60 整数。
提示:
1 <= time.length <= 600001 <= time[i] <= 500
解法
Python3
Java
class Solution {
public int numPairsDivisibleBy60(int[] time) {
Arrays.sort(time);
int ans = 0;
for (int i = 0; i < time.length - 1; i++) {
int num = (time[i] + time[time.length - 1]) / 60;
while (num > 0) {
int key = num * 60;
int index = Arrays.binarySearch(time, i + 1, time.length, key - time[i]);
if (index >= 0) {
int temp = index;
ans++;
while (++temp < time.length && time[temp] == time[index]) {
ans++;
}
temp = index;
while (--temp > i && time[temp] == time[index]) {
ans++;
}
}
num--;
}
}
return ans;
}
}
…
十进制的反码
问题描述
每个非负整数 N 都有其二进制表示。例如, 5 可以被表示为二进制 "101",11 可以用二进制 "1011" 表示,依此类推。注意,除 N = 0 外,任何二进制表示中都不含前导零。
二进制的反码表示是将每个 1 改为 0 且每个 0 变为 1。例如,二进制数 "101" 的二进制反码为 "010"。
给定十进制数 N,返回其二进制表示的反码所对应的十进制整数。
示例 1:
输入:5
输出:2
解释:5 的二进制表示为 "101",其二进制反码为 "010",也就是十进制中的 2 。
示例 2:
输入:7
输出:0
解释:7 的二进制表示为 "111",其二进制反码为 "000",也就是十进制中的 0 。
示例 3:
输入:10
输出:5
解释:10 的二进制表示为 "1010",其二进制反码为 "0101",也就是十进制中的 5 。
提示:
0 <= N < 10^9
解法
求余数,取反(0 -> 1, 1 -> 0),累加结果。
注意 N = 0 的特殊情况。
class Solution {
public int bitwiseComplement(int N) {
if (N == 0) return 1;
int res = 0;
int exp = 0;
while (N != 0) {
int bit = N % 2 == 0 ? 1 : 0;
res += Math.pow(2, exp) * bit;
++exp;
N >>= 1;
}
return res;
}
}
1017. 负二进制转换
English Version
题目描述
给出数字 N,返回由若干 "0" 和 "1"组成的字符串,该字符串为 N 的负二进制(base -2)表示。
除非字符串就是 "0",否则返回的字符串中不能含有前导零。
示例 1:
输入:2 输出:"110" 解释:(-2) ^ 2 + (-2) ^ 1 = 2
示例 2:
输入:3 输出:"111" 解释:(-2) ^ 2 + (-2) ^ 1 + (-2) ^ 0 = 3
示例 3:
输入:4 输出:"100" 解释:(-2) ^ 2 = 4
提示:
0 <= N <= 10^9
解法
Python3
Java
class Solution {
public String baseNeg2(int N) {
if (N == 0) {
return "0";
}
StringBuilder sb = new StringBuilder();
while (N != 0) {
sb.append(N & 1);
N = -(N >> 1);
}
return sb.reverse().toString();
}
}
…
1019. 链表中的下一个更大节点
English Version
题目描述
给出一个以头节点 head 作为第一个节点的链表。链表中的节点分别编号为:node_1, node_2, node_3, ... 。
每个节点都可能有下一个更大值(next larger value):对于 node_i,如果其 next_larger(node_i) 是 node_j.val,那么就有 j > i 且 node_j.val > node_i.val,而 j 是可能的选项中最小的那个。如果不存在这样的 j,那么下一个更大值为 0 。
返回整数答案数组 answer,其中 answer[i] = next_larger(node_{i+1}) 。
注意:在下面的示例中,诸如 [2,1,5] 这样的输入(不是输出)是链表的序列化表示,其头节点的值为 2,第二个节点值为 1,第三个节点值为 5 。
示例 1:
输入:[2,1,5] 输出:[5,5,0]
示例 2:
输入:[2,7,4,3,5] 输出:[7,0,5,5,0]
示例 3:
输入:[1,7,5,1,9,2,5,1] 输出:[7,9,9,9,0,5,0,0]
提示:
- 对于链表中的每个节点,
1 <= node.val <= 10^9 - 给定列表的长度在
[0, 10000]范围内
解法
Python3
Java
class Solution {
public int[] nextLargerNodes(ListNode head) {
List<Integer> list = new ArrayList<>();
while (head != null) {
list.add(head.val);
head = head.next;
}
int[] res = new int[list.size()];
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < list.size(); ++i) {
while (!stack.isEmpty() && list.get(i) > list.get(stack.peek())) {
res[stack.pop()] = list.get(i);
}
stack.push(i);
}
return res;
}
}
…
1021. 删除最外层的括号
English Version
题目描述
有效括号字符串为空 ("")、"(" + A + ")" 或 A + B,其中 A 和 B 都是有效的括号字符串,+ 代表字符串的连接。例如,"","()","(())()" 和 "(()(()))" 都是有效的括号字符串。
如果有效字符串 S 非空,且不存在将其拆分为 S = A+B 的方法,我们称其为原语(primitive),其中 A 和 B 都是非空有效括号字符串。
给出一个非空有效字符串 S,考虑将其进行原语化分解,使得:S = P_1 + P_2 + ... + P_k,其中 P_i 是有效括号字符串原语。
对 S 进行原语化分解,删除分解中每个原语字符串的最外层括号,返回 S 。
示例 1:
输入:"(()())(())" 输出:"()()()" 解释: 输入字符串为 "(()())(())",原语化分解得到 "(()())" + "(())", 删除每个部分中的最外层括号后得到 "()()" + "()" = "()()()"。
示例 2:
输入:"(()())(())(()(()))" 输出:"()()()()(())" 解释: 输入字符串为 "(()())(())(()(()))",原语化分解得到 "(()())" + "(())" + "(()(()))", 删除每隔部分中的最外层括号后得到 "()()" + "()" + "()(())" = "()()()()(())"。
示例 3:
输入:"()()" 输出:"" 解释: 输入字符串为 "()()",原语化分解得到 "()" + "()", 删除每个部分中的最外层括号后得到 "" + "" = ""。
提示:
S.length <= 10000S[i]为"("或")"S是一个有效括号字符串
解法
Python3
Java
class Solution {
public String removeOuterParentheses(String S) {
StringBuilder res = new StringBuilder();
int cnt = 0;
for (char c : S.toCharArray()) {
if (c == '(') {
if (++cnt > 1) {
res.append('(');
}
} else {
if (--cnt > 0) {
res.append(')');
}
}
}
return res.toString();
}
}
…
1022. 从根到叶的二进制数之和
English Version
题目描述
给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
以 10^9 + 7 为模,返回这些数字之和。
示例:
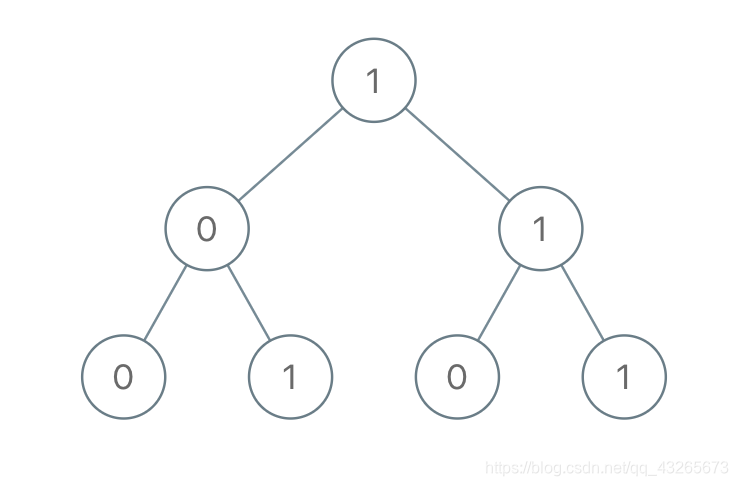输入:[1,0,1,0,1,0,1] 输出:22 解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
提示:
- 树中的结点数介于
1和1000之间。 - node.val 为
0或1。
解法
Python3
Java
class Solution {
public int sumRootToLeaf(TreeNode root) {
return dfs(root, 0);
}
private int dfs(TreeNode root, int s) {
if (root == null) {
return 0;
}
s = s << 1 | root.val;
if (root.left == null && root.right == null) {
return s;
}
return dfs(root.left, s) + dfs(root.right, s);
}
}
…
1025. 除数博弈
English Version
题目描述
爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作:
- 选出任一
x,满足0 < x < N且N % x == 0。 - 用
N - x替换黑板上的数字N。
如果玩家无法执行这些操作,就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 false。假设两个玩家都以最佳状态参与游戏。
示例 1:
输入:2 输出:true 解释:爱丽丝选择 1,鲍勃无法进行操作。
示例 2:
输入:3 输出:false 解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
提示:
1 <= N <= 1000
解法
Python3
Java
class Solution {
public boolean divisorGame(int N) {
return N % 2 == 0;
}
}
…
1026. 节点与其祖先之间的最大差值
English Version
题目描述
给定二叉树的根节点 root,找出存在于不同节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
示例:
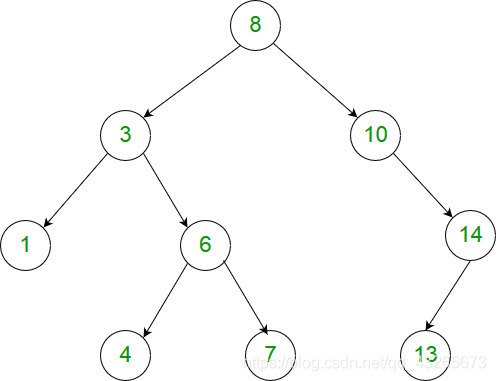输入:[8,3,10,1,6,null,14,null,null,4,7,13] 输出:7 解释: 我们有大量的节点与其祖先的差值,其中一些如下: |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 在所有可能的差值中,最大值 7 由 |8 - 1| = 7 得出。
提示:
- 树中的节点数在
2到5000之间。 - 每个节点的值介于
0到100000之间。
解法
Python3
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int bfs(TreeNode root, int max, int min) {
if (root == null) {
return 0;
}
int res = Math.max(max - root.val, root.val - min);
int mx = Math.max(root.val, max);
int mn = Math.min(root.val, min);
res = Math.max(res, bfs(root.left, mx, mn));
res = Math.max(res, bfs(root.right, mx, mn));
return res;
}
public int maxAncestorDiff(TreeNode root) {
return bfs(root, root.val, root.val);
}
}
…
1029. 两地调度
English Version
题目描述
公司计划面试 2N 人。第 i 人飞往 A 市的费用为 costs[i][0],飞往 B 市的费用为 costs[i][1]。
返回将每个人都飞到某座城市的最低费用,要求每个城市都有 N 人抵达。
示例:
输入:[[10,20],[30,200],[400,50],[30,20]] 输出:110 解释: 第一个人去 A 市,费用为 10。 第二个人去 A 市,费用为 30。 第三个人去 B 市,费用为 50。 第四个人去 B 市,费用为 20。 最低总费用为 10 + 30 + 50 + 20 = 110,每个城市都有一半的人在面试。
提示:
1 <= costs.length <= 100costs.length为偶数1 <= costs[i][0], costs[i][1] <= 1000
解法
Python3
Java
class Solution {
public int twoCitySchedCost(int[][] costs) {
Arrays.sort(costs, (a, b) -> {
return a[0] - a[1] - (b[0] - b[1]);
});
int sum = 0;
for (int i = 0; i < costs.length; ++i) {
if (i < costs.length / 2) {
sum += costs[i][0];
} else {
sum += costs[i][1];
}
}
return sum;
}
}
…
1030. 距离顺序排列矩阵单元格
English Version
题目描述
给出 R 行 C 列的矩阵,其中的单元格的整数坐标为 (r, c),满足 0 <= r < R 且 0 <= c < C。
另外,我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。
返回矩阵中的所有单元格的坐标,并按到 (r0, c0) 的距离从最小到最大的顺序排,其中,两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)
示例 1:
输入:R = 1, C = 2, r0 = 0, c0 = 0 输出:[[0,0],[0,1]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1]
示例 2:
输入:R = 2, C = 2, r0 = 0, c0 = 1 输出:[[0,1],[0,0],[1,1],[1,0]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2] [[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。
示例 3:
输入:R = 2, C = 3, r0 = 1, c0 = 2 输出:[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]] 解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2,2,3] 其他满足题目要求的答案也会被视为正确,例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。
提示:
1 <= R <= 1001 <= C <= 1000 <= r0 < R0 <= c0 < C
解法
Python3
Java
class Solution {
class Node {
int r;
int c;
public Node(int r, int c) {
this.r = r;
this.c = c;
}
}
public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
int[][] ans = new int[R * C][2];
int[][] flag = new int[R][C];
int index = 0;
ans[index][0] = r0;
ans[index][1] = c0;
index++;
flag[r0][c0] = 1;
LinkedList<Node> queue = new LinkedList<>();
queue.add(new Node(r0, c0));
while (!queue.isEmpty()) {
Node node = queue.removeFirst();
// up
if (node.r - 1 >= 0 && flag[node.r - 1][node.c] != 1) {
queue.add(new Node(node.r - 1, node.c));
flag[node.r - 1][node.c] = 1;
ans[index][0] = node.r - 1;
ans[index][1] = node.c;
index++;
}
// down
if (node.r + 1 < R && flag[node.r + 1][node.c] != 1) {
queue.add(new Node(node.r + 1, node.c));
flag[node.r + 1][node.c] = 1;
ans[index][0] = node.r + 1;
ans[index][1] = node.c;
index++;
}
// left
if (node.c - 1 >= 0 && flag[node.r][node.c - 1] != 1) {
queue.add(new Node(node.r, node.c - 1));
flag[node.r][node.c - 1] = 1;
ans[index][0] = node.r;
ans[index][1] = node.c - 1;
index++;
}
// right
if (node.c + 1 < C && flag[node.r][node.c + 1] != 1) {
queue.add(new Node(node.r, node.c + 1));
flag[node.r][node.c + 1] = 1;
ans[index][0] = node.r;
ans[index][1] = node.c + 1;
index++;
}
}
return ans;
}
}
…
1033. 移动石子直到连续
English Version
题目描述
三枚石子放置在数轴上,位置分别为 a,b,c。
每一回合,我们假设这三枚石子当前分别位于位置 x, y, z 且 x < y < z。从位置 x 或者是位置 z 拿起一枚石子,并将该石子移动到某一整数位置 k 处,其中 x < k < z 且 k != y。
当你无法进行任何移动时,即,这些石子的位置连续时,游戏结束。
要使游戏结束,你可以执行的最小和最大移动次数分别是多少? 以长度为 2 的数组形式返回答案:answer = [minimum_moves, maximum_moves]
示例 1:
输入:a = 1, b = 2, c = 5 输出:[1, 2] 解释:将石子从 5 移动到 4 再移动到 3,或者我们可以直接将石子移动到 3。
示例 2:
输入:a = 4, b = 3, c = 2 输出:[0, 0] 解释:我们无法进行任何移动。
提示:
1 <= a <= 1001 <= b <= 1001 <= c <= 100a != b, b != c, c != a
解法
Python3
Java
class Solution {
public int[] numMovesStones(int a, int b, int c) {
int x = Math.min(a, Math.min(b, c));
int z = Math.max(a, Math.max(b, c));
int y = a + b + c - x - z;
int max = z - x - 2;
int min = y - x == 1 && z - y == 1 ? 0 : y - x <= 2 || z - y <= 2 ? 1 : 2;
return new int[]{
min, max};
}
}
…
1034. 边框着色
English Version
题目描述
给出一个二维整数网格 grid,网格中的每个值表示该位置处的网格块的颜色。
只有当两个网格块的颜色相同,而且在四个方向中任意一个方向上相邻时,它们属于同一连通分量。
连通分量的边界是指连通分量中的所有与不在分量中的正方形相邻(四个方向上)的所有正方形,或者在网格的边界上(第一行/列或最后一行/列)的所有正方形。
给出位于 (r0, c0) 的网格块和颜色 color,使用指定颜色 color 为所给网格块的连通分量的边界进行着色,并返回最终的网格 grid 。
示例 1:
输入:grid = [[1,1],[1,2]], r0 = 0, c0 = 0, color = 3 输出:[[3, 3], [3, 2]]
示例 2:
输入:grid = [[1,2,2],[2,3,2]], r0 = 0, c0 = 1, color = 3 输出:[[1, 3, 3], [2, 3, 3]]
示例 3:
输入:grid = [[1,1,1],[1,1,1],[1,1,1]], r0 = 1, c0 = 1, color = 2 输出:[[2, 2, 2], [2, 1, 2], [2, 2, 2]]
提示:
1 <= grid.length <= 501 <= grid[0].length <= 501 <= grid[i][j] <= 10000 <= r0 < grid.length0 <= c0 < grid[0].length1 <= color <= 1000
解法
Python3
Java
class Solution {
private int[] dirs = new int[]{
-1, 0, 1, 0, -1};
public int[][] colorBorder(int[][] grid, int r0, int c0, int color) {
boolean[][] vis = new boolean[grid.length][grid[0].length];
dfs(grid, r0, c0, color, vis);
return grid;
}
private void dfs(int[][] grid, int i, int j, int color, boolean[][] vis) {
vis[i][j] = true;
int oldColor = grid[i][j];
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < grid.length && y >= 0 && y < grid[0].length) {
if (!vis[x][y]) {
if (grid[x][y] == oldColor) {
dfs(grid, x, y, color, vis);
} else {
grid[i][j] = color;
}
}
} else {
grid[i][j] = color;
}
}
}
}
…
1036. 逃离大迷宫
English Version
题目描述
在一个 10^6 x 10^6 的网格中,每个网格块的坐标为 (x, y),其中 0 <= x, y < 10^6。
我们从源方格 source 开始出发,意图赶往目标方格 target。每次移动,我们都可以走到网格中在四个方向上相邻的方格,只要该方格不在给出的封锁列表 blocked 上。
只有在可以通过一系列的移动到达目标方格时才返回 true。否则,返回 false。
示例 1:
输入:blocked = [[0,1],[1,0]], source = [0,0], target = [0,2] 输出:false 解释: 从源方格无法到达目标方格,因为我们无法在网格中移动。
示例 2:
输入:blocked = [], source = [0,0], target = [999999,999999] 输出:true 解释: 因为没有方格被封锁,所以一定可以到达目标方格。
提示:
0 <= blocked.length <= 200blocked[i].length == 20 <= blocked[i][j] < 10^6source.length == target.length == 20 <= source[i][j], target[i][j] < 10^6source != target
解法
Python3
Java
class Solution {
private static final int[] dx = {
0, 0, -1, 1};
private static final int[] dy = {
1, -1, 0, 0};
public boolean isEscapePossible(int[][] blocked, int[] source, int[] target) {
if (blocked.length < 2) {
return Boolean.TRUE;
}
return walk(blocked, source, target) && walk(blocked, target, source);
}
private Boolean walk(int[][] blocked, int[] source, int[] target) {
int N = 1000000;
Set<Pair<Integer, Integer>> visitSet = new HashSet<>();
Queue<Pair<Integer, Integer>> queue = new LinkedList<>();
Pair<Integer, Integer> start = new Pair<>(source[0], source[1]);
queue.add(start);
visitSet.add(start);
Set<Pair> blockedSet = Arrays.stream(blocked).map(item -> new Pair(item[0], item[1])).collect(Collectors.toSet());
while (!queue.isEmpty()) {
Pair<Integer, Integer> top = queue.poll();
Integer x = top.getKey();
Integer y = top.getValue();
for (int i = 0; i < 4; i++) {
int newY = y + dy[i];
int newX = x + dx[i];
Pair<Integer, Integer> pair = new Pair<>(newX, newY);
if (newX < 0 || newY < 0 || newX >= N || newY >= N || visitSet.contains(pair) || blockedSet.contains(pair)) {
continue;
}
queue.add(pair);
visitSet.add(pair);
if (queue.size() >= blocked.length || (newX == target[0] && newY == target[1])) {
return Boolean.TRUE;
}
}
}
return Boolean.FALSE;
}
}
…
1037. 有效的回旋镖
English Version
题目描述
回旋镖定义为一组三个点,这些点各不相同且不在一条直线上。
给出平面上三个点组成的列表,判断这些点是否可以构成回旋镖。
示例 1:
输入:[[1,1],[2,3],[3,2]] 输出:true
示例 2:
输入:[[1,1],[2,2],[3,3]] 输出:false
提示:
points.length == 3points[i].length == 20 <= points[i][j] <= 100
解法
Python3
Java
class Solution {
public boolean isBoomerang(int[][] points) {
double temp1;
double temp2;
double temp3;
Arrays.sort(points, new Comparator<int[]>() {
@Override
public int compare(int[] ints, int[] t1) {
return ints[0] - t1[0];
}
});
if (points[0][0] == points[1][0]) {
if (points[0][1] == points[1][1])
return false;
temp1 = 1;
} else {
temp1 = (points[0][1] - points[1][1]) * 1.0 / (points[0][0] - points[1][0]);
}
if (points[1][0] == points[2][0]) {
if (points[1][1] == points[2][1])
return false;
temp2 = 1;
} else {
temp2 = (points[1][1] - points[2][1]) * 1.0 / (points[1][0] - points[2][0]);
}
if (points[0][0] == points[2][0]) {
if (points[0][1] == points[2][1])
return false;
temp3 = 1;
} else {
temp3 = (points[0][1] - points[2][1]) * 1.0 / (points[0][0] - points[2][0]);
}
if (temp1 == temp2 && temp1 == temp3 && temp2 == temp3) {
return false;
} else {
return true;
}
}
}
…
1038. 从二叉搜索树到更大和树
English Version
题目描述
给出二叉 搜索 树的根节点,该二叉树的节点值各不相同,修改二叉树,使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例:
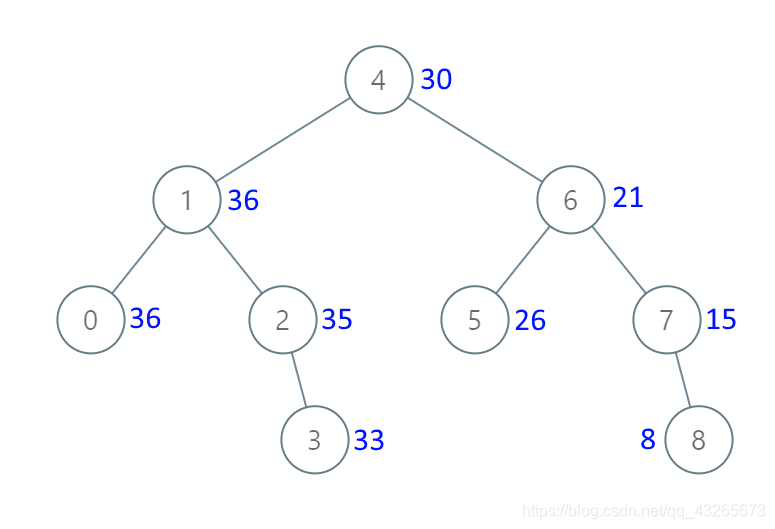输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
提示:
- 树中的节点数介于
1和100之间。 - 每个节点的值介于
0和100之间。 - 给定的树为二叉搜索树。
注意:该题目与 538: https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ 相同
解法
Python3
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private int max = 0;
public TreeNode bstToGst(TreeNode root) {
if (root == null) return new TreeNode(0);
int temp = bstToGst(root.right).val;
root.val += (temp > max ? temp : max);
max = root.val > max ? root.val : max;
if (root.left != null) {
int temp2 = bstToGst(root.left.right).val;
root.left.val += max > temp2 ? max : temp2;
max = max > root.left.val ? max : root.left.val;
bstToGst(root.left.left);
}
return root;
}
}
…
1041. 困于环中的机器人
English Version
题目描述
在无限的平面上,机器人最初位于 (0, 0) 处,面朝北方。机器人可以接受下列三条指令之一:
"G":直走 1 个单位"L":左转 90 度"R":右转 90 度
机器人按顺序执行指令 instructions,并一直重复它们。
只有在平面中存在环使得机器人永远无法离开时,返回 true。否则,返回 false。
示例 1:
输入:"GGLLGG" 输出:true 解释: 机器人从 (0,0) 移动到 (0,2),转 180 度,然后回到 (0,0)。 重复这些指令,机器人将保持在以原点为中心,2 为半径的环中进行移动。
示例 2:
输入:"GG" 输出:false 解释: 机器人无限向北移动。
示例 3:
输入:"GL" 输出:true 解释: 机器人按 (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ... 进行移动。
提示:
1 <= instructions.length <= 100instructions[i]在{'G', 'L', 'R'}中
解法
Python3
Java
class Solution {
public boolean isRobotBounded(String instructions) {
int col = 0;
int row = 0;
char[] orders = instructions.toCharArray();
int order = 0;
for (int i = 0; i < 4; i++) {
for (char ch : orders) {
if (ch == 'L') {
order--;
if (order == -3) {
order = 1;
}
} else if (ch == 'R') {
order++;
if (order == 2) {
order = -2;
}
} else {
switch (order) {
case 0:
row++;
break;
case 1:
col++;
break;
case -1:
col--;
break;
case -2:
row--;
break;
default:
break;
}
}
}
if (col == 0 && row == 0) {
return true;
}
}
return false;
}
}
…
1043. 分隔数组以得到最大和
English Version
题目描述
给出整数数组 A,将该数组分隔为长度最多为 K 的几个(连续)子数组。分隔完成后,每个子数组的中的值都会变为该子数组中的最大值。
返回给定数组完成分隔后的最大和。
示例:
输入:A = [1,15,7,9,2,5,10], K = 3 输出:84 解释:A 变为 [15,15,15,9,10,10,10]
提示:
1 <= K <= A.length <= 5000 <= A[i] <= 10^6
解法
Python3
Java
class Solution {
public int maxSumAfterPartitioning(int[] A, int K) {
int[] dp = new int[A.length];
int max = 0;
for (int i = 0; i < A.length; i++) {
max = 0;
for (int k = 0; k < K && i - k >= 0; k++) {
max = Math.max(max, A[i - k]);
dp[i] = Math.max(dp[i], (i - 1 >= k ? dp[i - k - 1] : 0) + max * (k + 1));
}
}
return dp[A.length - 1];
}
}
…
1046. 最后一块石头的重量
English Version
题目描述
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出两块最重的石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下,就返回 0。
提示:
1 <= stones.length <= 301 <= stones[i] <= 1000
解法
Python3
Java
class Solution {
public int lastStoneWeight(int[] stones) {
Queue<Integer> queue = new PriorityQueue<>(Comparator.reverseOrder());
for (int stone : stones) {
queue.offer(stone);
}
while (queue.size() > 1) {
int x = queue.poll();
int y = queue.poll();
if (x != y) {
queue.offer(x - y);
}
}
return queue.isEmpty() ? 0 : queue.poll();
}
}
…
1047. 删除字符串中的所有相邻重复项
English Version
题目描述
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:"abbaca" 输出:"ca" 解释: 例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
提示:
1 <= S.length <= 20000S仅由小写英文字母组成。
解法
Python3
Java
class Solution {
public String removeDuplicates(String S) {
char[] cs = new char[S.length()];
int top = -1;
for (char c : S.toCharArray()) {
if (top >= 0 && c == cs[top]) {
--top;
} else {
cs[++top] = c;
}
}
return String.valueOf(cs, 0, top + 1);
}
}
…
1048. 最长字符串链
English Version
题目描述
给出一个单词列表,其中每个单词都由小写英文字母组成。
如果我们可以在 word1 的任何地方添加一个字母使其变成 word2,那么我们认为 word1 是 word2 的前身。例如,"abc" 是 "abac" 的前身。
词链是单词 [word_1, word_2, ..., word_k] 组成的序列,k >= 1,其中 word_1 是 word_2 的前身,word_2 是 word_3 的前身,依此类推。
从给定单词列表 words 中选择单词组成词链,返回词链的最长可能长度。
示例:
输入:["a","b","ba","bca","bda","bdca"] 输出:4 解释:最长单词链之一为 "a","ba","bda","bdca"。
提示:
1 <= words.length <= 10001 <= words[i].length <= 16words[i]仅由小写英文字母组成。
解法
Python3
Java
class Solution {
public int longestStrChain(String[] words) {
Arrays.sort(words, new Comparator<String>() {
@Override
public int compare(String o1, String o2) {
return Integer.compare(o1.length(), o2.length());
}
});
int res = 0;
Map<String, Integer> map = new HashMap<>();
for (String word : words) {
int x = 1;
for (int i = 0; i < word.length(); ++i) {
String pre = word.substring(0, i) + word.substring(i + 1);
x = Math.max(x, map.getOrDefault(pre, 0) + 1);
}
map.put(word, x);
res = Math.max(res, x);
}
return res;
}
}
…
1051. 高度检查器
English Version
题目描述
学校在拍年度纪念照时,一般要求学生按照 非递减 的高度顺序排列。
请你返回能让所有学生以 非递减 高度排列的最小必要移动人数。
注意,当一组学生被选中时,他们之间可以以任何可能的方式重新排序,而未被选中的学生应该保持不动。
示例:
输入:heights = [1,1,4,2,1,3] 输出:3 解释: 当前数组:[1,1,4,2,1,3] 目标数组:[1,1,1,2,3,4] 在下标 2 处(从 0 开始计数)出现 4 vs 1 ,所以我们必须移动这名学生。 在下标 4 处(从 0 开始计数)出现 1 vs 3 ,所以我们必须移动这名学生。 在下标 5 处(从 0 开始计数)出现 3 vs 4 ,所以我们必须移动这名学生。
示例 2:
输入:heights = [5,1,2,3,4] 输出:5
示例 3:
输入:heights = [1,2,3,4,5] 输出:0
提示:
1 <= heights.length <= 1001 <= heights[i] <= 100
解法
Python3
Java
class Solution {
public int heightChecker(int[] heights) {
int[] copy = Arrays.copyOf(heights, heights.length);
Arrays.sort(copy);
int res = 0;
for (int i = 0; i < heights.length; ++i) {
if (heights[i] != copy[i]) {
++res;
}
}
return res;
}
}
…
1052. 爱生气的书店老板
English Version
题目描述
今天,书店老板有一家店打算试营业 customers.length 分钟。每分钟都有一些顾客(customers[i])会进入书店,所有这些顾客都会在那一分钟结束后离开。
在某些时候,书店老板会生气。 如果书店老板在第 i 分钟生气,那么 grumpy[i] = 1,否则 grumpy[i] = 0。 当书店老板生气时,那一分钟的顾客就会不满意,不生气则他们是满意的。
书店老板知道一个秘密技巧,能抑制自己的情绪,可以让自己连续 X 分钟不生气,但却只能使用一次。
请你返回这一天营业下来,最多有多少客户能够感到满意的数量。
示例:
输入:customers = [1,0,1,2,1,1,7,5], grumpy = [0,1,0,1,0,1,0,1], X = 3 输出:16 解释: 书店老板在最后 3 分钟保持冷静。 感到满意的最大客户数量 = 1 + 1 + 1 + 1 + 7 + 5 = 16.
提示:
1 <= X <= customers.length == grumpy.length <= 200000 <= customers[i] <= 10000 <= grumpy[i] <= 1
解法
- 用
s累计不使用秘密技巧时,满意的顾客数; - 用
t计算大小为X的滑动窗口最多增加的满意的顾客数; - 结果即为
s+t。
Python3
class Solution:
def maxSatisfied(self, customers: List[int], grumpy: List[int], X: int) -> int:
# 用s累计不使用秘密技巧时,满意的顾客数
# 用t计算大小为X的滑动窗口最多增加的满意的顾客数
# 结果即为s+t
s = t = 0
win, n = 0, len(customers)
for i in range(n):
if grumpy[i] == 0:
s += customers[i]
else:
win += customers[i]
if i >= X and grumpy[i - X] == 1:
win -= customers[i - X]
# 求滑动窗口的最大值
t = max(t, win)
return s + t
Java
class Solution {
public int maxSatisfied(int[] customers, int[] grumpy, int X) {
// 用s累计不使用秘密技巧时,满意的顾客数
// 用t计算大小为X的滑动窗口最多增加的满意的顾客数
// 结果即为s+t
int s = 0, t = 0;
for (int i = 0, win = 0, n = customers.length; i < n; ++i) {
if (grumpy[i] == 0) {
s += customers[i];
} else {
win += customers[i];
}
if (i >= X && grumpy[i - X] == 1) {
win -= customers[i - X];
}
// 求滑动窗口的最大值
t = Math.max(t, win);
}
return s + t;
}
}
…
1053. 交换一次的先前排列
English Version
题目描述
给你一个正整数的数组 A(其中的元素不一定完全不同),请你返回可在 一次交换(交换两数字 A[i] 和 A[j] 的位置)后得到的、按字典序排列小于 A 的最大可能排列。
如果无法这么操作,就请返回原数组。
示例 1:
输入:[3,2,1] 输出:[3,1,2] 解释: 交换 2 和 1
示例 2:
输入:[1,1,5] 输出:[1,1,5] 解释: 这已经是最小排列
示例 3:
输入:[1,9,4,6,7] 输出:[1,7,4,6,9] 解释: 交换 9 和 7
示例 4:
输入:[3,1,1,3] 输出:[1,3,1,3] 解释: 交换 1 和 3
提示:
1 <= A.length <= 100001 <= A[i] <= 10000
解法
Python3
Java
class Solution {
public int[] prevPermOpt1(int[] A) {
for (int i = A.length - 2; i >= 0; --i) {
if (A[i] > A[i + 1]) {
int k = i + 1;
for (int j = k + 1; j < A.length; ++j) {
if (A[j] < A[i] && A[j] > A[k]) {
k = j;
}
}
int t = A[i];
A[i] = A[k];
A[k] = t;
return A;
}
}
return A;
}
}
…
1054. 距离相等的条形码
English Version
题目描述
在一个仓库里,有一排条形码,其中第 i 个条形码为 barcodes[i]。
请你重新排列这些条形码,使其中两个相邻的条形码 不能 相等。 你可以返回任何满足该要求的答案,此题保证存在答案。
示例 1:
输入:[1,1,1,2,2,2] 输出:[2,1,2,1,2,1]
示例 2:
输入:[1,1,1,1,2,2,3,3] 输出:[1,3,1,3,2,1,2,1]
提示:
1 <= barcodes.length <= 100001 <= barcodes[i] <= 10000
解法
Python3
Java
class Solution {
public int[] rearrangeBarcodes(int[] barcodes) {
Map<Integer, Integer> map = new HashMap<>();
for (int x : barcodes) {
map.put(x, map.getOrDefault(x, 0) + 1);
}
Data[] ds = new Data[map.size()];
int i = 0;
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
ds[i++] = new Data(entry.getKey(), entry.getValue());
}
Arrays.sort(ds);
i = 0;
for (Data d : ds) {
while (d.cnt-- > 0) {
barcodes[i] = d.x;
i += 2;
if (i >= barcodes.length) {
i = 1;
}
}
}
return barcodes;
}
class Data implements Comparable<Data> {
int x, cnt;
public Data(int x, int cnt) {
this.x = x;
this.cnt = cnt;
}
@Override
public int compareTo(Data o) {
return Integer.compare(o.cnt, cnt);
}
}
}
…
1071. 字符串的最大公因子
English Version
题目描述
对于字符串 S 和 T,只有在 S = T + ... + T(T 与自身连接 1 次或多次)时,我们才认定 “T 能除尽 S”。
返回最长字符串 X,要求满足 X 能除尽 str1 且 X 能除尽 str2。
示例 1:
输入:str1 = "ABCABC", str2 = "ABC" 输出:"ABC"
示例 2:
输入:str1 = "ABABAB", str2 = "ABAB" 输出:"AB"
示例 3:
输入:str1 = "LEET", str2 = "CODE" 输出:""
提示:
1 <= str1.length <= 10001 <= str2.length <= 1000str1[i]和str2[i]为大写英文字母
解法
Python3
Java
class Solution {
public String gcdOfStrings(String str1, String str2) {
if (!(str1 + str2).equals(str2 + str1)) {
return "";
}
int len = gcd(str1.length(), str2.length());
return str1.substring(0, len);
}
private int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
}
…
1072. 按列翻转得到最大值等行数
English Version
题目描述
给定由若干 0 和 1 组成的矩阵 matrix,从中选出任意数量的列并翻转其上的 每个 单元格。翻转后,单元格的值从 0 变成 1,或者从 1 变为 0 。
返回经过一些翻转后,行上所有值都相等的最大行数。
示例 1:
输入:[[0,1],[1,1]] 输出:1 解释:不进行翻转,有 1 行所有值都相等。
示例 2:
输入:[[0,1],[1,0]] 输出:2 解释:翻转第一列的值之后,这两行都由相等的值组成。
示例 3:
输入:[[0,0,0],[0,0,1],[1,1,0]] 输出:2 解释:翻转前两列的值之后,后两行由相等的值组成。
提示:
1 <= matrix.length <= 3001 <= matrix[i].length <= 300- 所有
matrix[i].length都相等 matrix[i][j]为0或1
解法
Python3
Java
class Solution {
public int maxEqualRowsAfterFlips(int[][] matrix) {
Map<String, Integer> map = new HashMap<>();
for (int[] row : matrix) {
if (row[0] == 1) {
for (int i = 0; i < row.length; ++i) {
row[i] ^= 1;
}
}
StringBuilder sb = new StringBuilder();
for (int x : row) {
sb.append(x);
}
String s = sb.toString();
map.put(s, map.getOrDefault(s, 0) + 1);
}
return map.values().stream().max(Integer::compareTo).get();
}
}
…
1073. 负二进制数相加
English Version
题目描述
给出基数为 -2 的两个数 arr1 和 arr2,返回两数相加的结果。
数字以 数组形式 给出:数组由若干 0 和 1 组成,按最高有效位到最低有效位的顺序排列。例如,arr = [1,1,0,1] 表示数字 (-2)^3 + (-2)^2 + (-2)^0 = -3。数组形式 的数字也同样不含前导零:以 arr 为例,这意味着要么 arr == [0],要么 arr[0] == 1。
返回相同表示形式的 arr1 和 arr2 相加的结果。两数的表示形式为:不含前导零、由若干 0 和 1 组成的数组。
示例:
输入:arr1 = [1,1,1,1,1], arr2 = [1,0,1] 输出:[1,0,0,0,0] 解释:arr1 表示 11,arr2 表示 5,输出表示 16 。
提示:
1 <= arr1.length <= 10001 <= arr2.length <= 1000arr1和arr2都不含前导零arr1[i]为0或1arr2[i]为0或1
解法
Python3
Java
class Solution {
public int[] addNegabinary(int[] arr1, int[] arr2) {
List<Integer> list = new ArrayList<>();
int carry = 0;
for (int i = arr1.length - 1, j = arr2.length - 1; i >= 0 || j >= 0 || carry != 0; --i, --j) {
carry += (i >= 0 ? arr1[i] : 0) + (j >= 0 ? arr2[j] : 0);
list.add(carry & 1);
carry = -(carry >> 1);
}
while (list.size() > 1 && list.get(list.size() - 1) == 0) {
list.remove(list.size() - 1);
}
Collections.reverse(list);
return list.stream().mapToInt(x -> x).toArray();
}
}
…
1074. 元素和为目标值的子矩阵数量
English Version
题目描述
给出矩阵 matrix 和目标值 target,返回元素总和等于目标值的非空子矩阵的数量。
子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。
如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同(如:x1 != x1'),那么这两个子矩阵也不同。
示例 1:
输入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0 输出:4 解释:四个只含 0 的 1x1 子矩阵。
示例 2:
输入:matrix = [[1,-1],[-1,1]], target = 0 输出:5 解释:两个 1x2 子矩阵,加上两个 2x1 子矩阵,再加上一个 2x2 子矩阵。
提示:
1 <= matrix.length <= 3001 <= matrix[0].length <= 300-1000 <= matrix[i] <= 1000-10^8 <= target <= 10^8
解法
Python3
Java
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int row = matrix.length, col = matrix[0].length;
int[][] sum = new int[row][col];
int ans = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (i == 0 && j == 0) {
sum[i][j] = matrix[i][j];
} else if (i == 0) {
sum[i][j] = matrix[i][j] + sum[i][j - 1];
} else if (j == 0) {
sum[i][j] = matrix[i][j] + sum[i - 1][j];
} else {
sum[i][j] = matrix[i][j] - sum[i - 1][j - 1] + sum[i - 1][j] + sum[i][j - 1];
}
for (int k = 0; k <= i; k++) {
for (int l = 0; l <= j; l++) {
int main = (k != 0 && l != 0) ? sum[k - 1][l - 1] : 0;
int left = k != 0 ? sum[k - 1][j] : 0;
int up = l != 0 ? sum[i][l - 1] : 0;
if (sum[i][j] - left - up + main == target) {
ans++;
}
}
}
}
}
return ans;
}
}
…
1079. 活字印刷
English Version
题目描述
你有一套活字字模 tiles,其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。
示例 1:
输入:"AAB" 输出:8 解释:可能的序列为 "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA"。
示例 2:
输入:"AAABBC" 输出:188
提示:
1 <= tiles.length <= 7tiles由大写英文字母组成
解法
Python3
Java
class Solution {
public int numTilePossibilities(String tiles) {
int[] cnt = new int[26];
for (char c : tiles.toCharArray()) {
++cnt[c - 'A'];
}
return dfs(cnt);
}
private int dfs(int[] cnt) {
int res = 0;
for (int i = 0; i < cnt.length; ++i) {
if (cnt[i] > 0) {
++res;
--cnt[i];
res += dfs(cnt);
++cnt[i];
}
}
return res;
}
}
…
1080. 根到叶路径上的不足节点
English Version
题目描述
给定一棵二叉树的根 root,请你考虑它所有 从根到叶的路径:从根到任何叶的路径。(所谓一个叶子节点,就是一个没有子节点的节点)
假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为「不足节点」,需要被删除。
请你删除所有不足节点,并返回生成的二叉树的根。
示例 1:
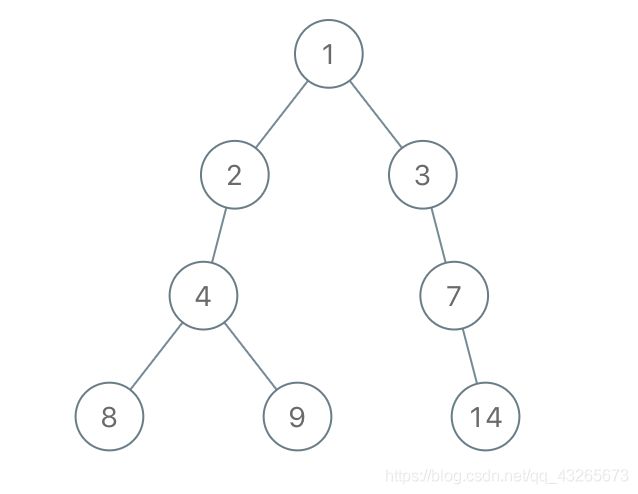
输入:root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出:[1,2,3,4,null,null,7,8,9,null,14]
示例 2:
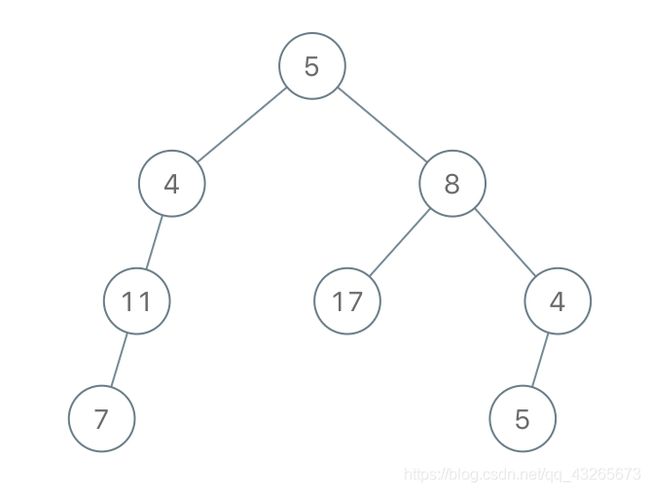
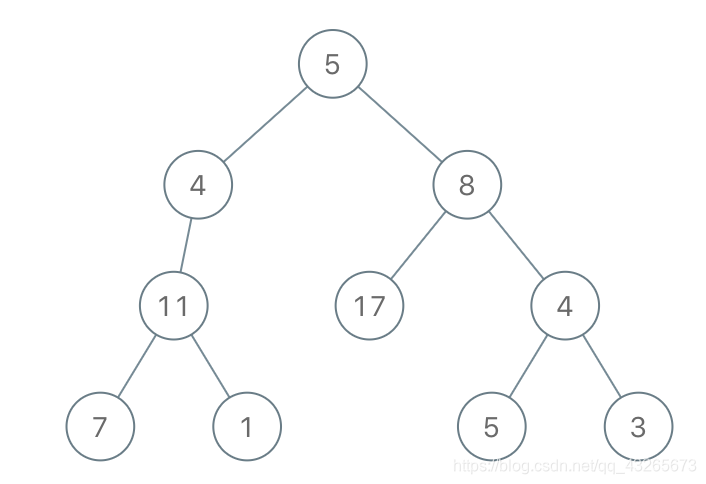输入:root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出:[5,4,8,11,null,17,4,7,null,null,null,5]
示例 3:
输入:root = [5,-6,-6], limit = 0 输出:[]
提示:
- 给定的树有
1到5000个节点 -10^5 <= node.val <= 10^5-10^9 <= limit <= 10^9
解法
Python3
Java
class Solution {
public TreeNode sufficientSubset(TreeNode root, int limit) {
if (root == null) {
return null;
}
limit -= root.val;
if (root.left == null && root.right == null) {
return limit > 0 ? null : root;
}
root.left = sufficientSubset(root.left, limit);
root.right = sufficientSubset(root.right, limit);
return root.left == null && root.right == null ? null : root;
}
}
…
1081. 不同字符的最小子序列
English Version
题目描述
返回字符串 text 中按字典序排列最小的子序列,该子序列包含 text 中所有不同字符一次。
示例 1:
输入:"cdadabcc" 输出:"adbc"
示例 2:
输入:"abcd" 输出:"abcd"
示例 3:
输入:"ecbacba" 输出:"eacb"
示例 4:
输入:"leetcode" 输出:"letcod"
提示:
1 <= text.length <= 1000text由小写英文字母组成
注意:本题目与 316 https://leetcode-cn.com/problems/remove-duplicate-letters/ 相同
解法
Python3
Java
class Solution {
public String smallestSubsequence(String text) {
int[] cnt = new int[26];
for (char c : text.toCharArray()) {
++cnt[c - 'a'];
}
boolean[] vis = new boolean[26];
char[] cs = new char[text.length()];
int top = -1;
for (char c : text.toCharArray()) {
--cnt[c - 'a'];
if (!vis[c - 'a']) {
while (top >= 0 && c < cs[top] && cnt[cs[top] - 'a'] > 0) {
vis[cs[top--] - 'a'] = false;
}
cs[++top] = c;
vis[c - 'a'] = true;
}
}
return String.valueOf(cs, 0, top + 1);
}
}
…
1089. 复写零
English Version
题目描述
给你一个长度固定的整数数组 arr,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。
要求:请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:[1,0,2,3,0,4,5,0] 输出:null 解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]
示例 2:
输入:[1,2,3] 输出:null 解释:调用函数后,输入的数组将被修改为:[1,2,3]
提示:
1 <= arr.length <= 100000 <= arr[i] <= 9
解法
Python3
Java
class Solution {
public void duplicateZeros(int[] arr) {
int n = arr.length;
int i = 0, j = 0;
while (j < n) {
if (arr[i] == 0) ++j;
++i;
++j;
}
--i; // i 回到最后一次合法的位置
--j; // j 同理,但 j 仍可能等于 n(例如输入 [0])
while (i >= 0) {
if (j < n) arr[j] = arr[i];
if (arr[i] == 0) arr[--j] = arr[i];
--i;
--j;
}
}
}
…
1090. 受标签影响的最大值
English Version
题目描述
我们有一个项的集合,其中第 i 项的值为 values[i],标签为 labels[i]。
我们从这些项中选出一个子集 S,这样一来:
|S| <= num_wanted- 对于任意的标签
L,子集S中标签为L的项的数目总满足<= use_limit。
返回子集 S 的最大可能的 和。
示例 1:
输入:values = [5,4,3,2,1], labels = [1,1,2,2,3], num_wanted = 3, use_limit = 1
输出:9
解释:选出的子集是第一项,第三项和第五项。
示例 2:
输入:values = [5,4,3,2,1], labels = [1,3,3,3,2], num_wanted = 3, use_limit = 2
输出:12
解释:选出的子集是第一项,第二项和第三项。
示例 3:
输入:values = [9,8,8,7,6], labels = [0,0,0,1,1], num_wanted = 3, use_limit = 1
输出:16
解释:选出的子集是第一项和第四项。
示例 4:
输入:values = [9,8,8,7,6], labels = [0,0,0,1,1], num_wanted = 3, use_limit = 2
输出:24
解释:选出的子集是第一项,第二项和第四项。
提示:
1 <= values.length == labels.length <= 200000 <= values[i], labels[i] <= 200001 <= num_wanted, use_limit <= values.length
解法
Python3
Java
class Solution {
public int largestValsFromLabels(int[] values, int[] labels, int num_wanted, int use_limit) {
class Data implements Comparable<Data> {
int value, label;
public Data(int value, int label) {
this.value = value;
this.label = label;
}
@Override
public int compareTo(Data o) {
return Integer.compare(o.value, this.value);
}
}
int n = values.length;
Data[] ds = new Data[n];
for (int i = 0; i < n; ++i) {
ds[i] = new Data(values[i], labels[i]);
}
Arrays.sort(ds);
int[] map = new int[20001];
int res = 0;
for (int i = 0; i < n && num_wanted != 0; ++i) {
if (++map[ds[i].label] <= use_limit) {
res += ds[i].value;
--num_wanted;
}
}
return res;
}
}
…
1091. 二进制矩阵中的最短路径
English Version
题目描述
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, ..., C_k 组成:
- 相邻单元格
C_i和C_{i+1}在八个方向之一上连通(此时,C_i和C_{i+1}不同且共享边或角) C_1位于(0, 0)(即,值为grid[0][0])C_k位于(N-1, N-1)(即,值为grid[N-1][N-1])- 如果
C_i位于(r, c),则grid[r][c]为空(即,grid[r][c] == 0)
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。
示例 1:
输入:[[0,1],[1,0]]
输出:2
示例 2:
输入:[[0,0,0],[1,1,0],[1,1,0]]
输出:4
提示:
1 <= grid.length == grid[0].length <= 100grid[i][j]为0或1
解法
Python3
Java
class Solution {
public int shortestPathBinaryMatrix(int[][] grid) {
int n = grid.length;
if (grid[0][0] == 1 || grid[n - 1][n - 1] == 1) {
return -1;
}
Queue<int[]> queue = new ArrayDeque<>();
boolean[][] vis = new boolean[n][n];
queue.offer(new int[]{
0, 0});
vis[0][0] = true;
int[][] dirs = new int[][]{
{
0, 1}, {
1, 1}, {
1, 0}, {
1, -1}, {
0, -1}, {
-1, -1}, {
-1, 0}, {
-1, 1}};
int res = 1;
while (!queue.isEmpty()) {
int size = queue.size();
while (size-- != 0) {
int[] cur = queue.poll();
if (cur[0] == n - 1 && cur[1] == n - 1) {
return res;
}
for (int[] dir : dirs) {
int x = cur[0] + dir[0], y = cur[1] + dir[1];
if (x >= 0 && x < n && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 0) {
vis[x][y] = true;
queue.offer(new int[]{
x, y});
}
}
}
++res;
}
return -1;
}
}
…
1093. 大样本统计
English Version
题目描述
我们对 0 到 255 之间的整数进行采样,并将结果存储在数组 count 中:count[k] 就是整数 k 的采样个数。
我们以 浮点数 数组的形式,分别返回样本的最小值、最大值、平均值、中位数和众数。其中,众数是保证唯一的。
我们先来回顾一下中位数的知识:
- 如果样本中的元素有序,并且元素数量为奇数时,中位数为最中间的那个元素;
- 如果样本中的元素有序,并且元素数量为偶数时,中位数为中间的两个元素的平均值。
示例 1:
输入:count = [0,1,3,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] 输出:[1.00000,3.00000,2.37500,2.50000,3.00000]
示例 2:
输入:count = [0,4,3,2,2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] 输出:[1.00000,4.00000,2.18182,2.00000,1.00000]
提示:
count.length == 2561 <= sum(count) <= 10^9- 计数表示的众数是唯一的
- 答案与真实值误差在
10^-5以内就会被视为正确答案
解法
Python3
Java
class Solution {
public double[] sampleStats(int[] count) {
int n = count.length;
int mode = 0, modeMax = 0;
int min = -1, max = -1;
double avg = 0;
int cnt = 0;
for (int i = 0; i < n; ++i) {
if (count[i] > modeMax) {
modeMax = count[i];
mode = i;
}
if (count[i] != 0) {
cnt += count[i];
avg += count[i] * i;
if (min == -1) min = i;
max = i;
}
}
avg /= cnt;
// 求中位数
double mid = 0;
int sum = 0;
for (int i = 0; i < n; ++i) {
sum += count[i];
if (sum << 1 > cnt) {
mid = i;
break;
} else if (sum << 1 == cnt) {
for (int j = i + 1; j < n; ++j) {
if (count[j] != 0) {
mid = (i + j) / 2.0;
break;
}
}
break;
}
}
return new double[]{
min, max, avg, mid, mode};
}
}
…
1094. 拼车
English Version
题目描述
假设你是一位顺风车司机,车上最初有 capacity 个空座位可以用来载客。由于道路的限制,车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向,你可以将其想象为一个向量)。
这儿有一份行程计划表 trips[][],其中 trips[i] = [num_passengers, start_location, end_location] 包含了你的第 i 次行程信息:
- 必须接送的乘客数量;
- 乘客的上车地点;
- 以及乘客的下车地点。
这些给出的地点位置是从你的 初始 出发位置向前行驶到这些地点所需的距离(它们一定在你的行驶方向上)。
请你根据给出的行程计划表和车子的座位数,来判断你的车是否可以顺利完成接送所用乘客的任务(当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false)。
示例 1:
输入:trips = [[2,1,5],[3,3,7]], capacity = 4 输出:false
示例 2:
输入:trips = [[2,1,5],[3,3,7]], capacity = 5 输出:true
示例 3:
输入:trips = [[2,1,5],[3,5,7]], capacity = 3 输出:true
示例 4:
输入:trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11 输出:true
提示:
- 你可以假设乘客会自觉遵守 “先下后上” 的良好素质
trips.length <= 1000trips[i].length == 31 <= trips[i][0] <= 1000 <= trips[i][1] < trips[i][2] <= 10001 <= capacity <= 100000
解法
Python3
Java
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int[] cnt = new int[1001];
for (int[] trip : trips) {
cnt[trip[1]] += trip[0];
cnt[trip[2]] -= trip[0];
}
if (cnt[0] > capacity) return false;
for (int i = 1; i < 1001; ++i) {
cnt[i] += cnt[i - 1];
if (cnt[i] > capacity) {
return false;
}
}
return true;
}
}
…
1095. 山脉数组中查找目标值
English Version
题目描述
(这是一个 交互式问题 )
给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
所谓山脉数组,即数组 A 假如是一个山脉数组的话,需要满足如下条件:
首先,A.length >= 3
其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i]A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k)- 会返回数组中索引为k的元素(下标从 0 开始)MountainArray.length()- 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
为了帮助大家更好地理解交互式问题,我们准备了一个样例 “答案”:https://leetcode-cn.com/playground/RKhe3ave,请注意这 不是一个正确答案。
示例 1:
输入:array = [1,2,3,4,5,3,1], target = 3 输出:2 解释:3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
示例 2:
输入:array = [0,1,2,4,2,1], target = 3 输出:-1 解释:3 在数组中没有出现,返回 -1。
提示:
3 <= mountain_arr.length() <= 100000 <= target <= 10^90 <= mountain_arr.get(index) <= 10^9
解法
Python3
Java
class Solution {
public int findInMountainArray(int target, MountainArray mountainArr) {
int length = mountainArr.length();
int l = 0, r = length - 1;
while (l < r) {
int mid = l + r >>> 1;
if (mountainArr.get(mid) > mountainArr.get(mid + 1)) r = mid;
else l = mid + 1;
}
int topIndex = r;
int topValue = mountainArr.get(topIndex);
if (target == topValue) return topIndex;
if (target > topValue) return -1;
l = 0;
r = topIndex - 1;
while (l < r) {
int mid = l + r >>> 1;
if (mountainArr.get(mid) >= target) r = mid;
else l = mid + 1;
}
if (mountainArr.get(r) == target) {
return r;
}
l = topIndex + 1;
r = length - 1;
while (l < r) {
int mid = l + r >>> 1;
if (mountainArr.get(mid) <= target) r = mid;
else l = mid + 1;
}
return mountainArr.get(r) == target ? r : -1;
}
}
…
1103. 分糖果 II
English Version
题目描述
排排坐,分糖果。
我们买了一些糖果 candies,打算把它们分给排好队的 n = num_people 个小朋友。
给第一个小朋友 1 颗糖果,第二个小朋友 2 颗,依此类推,直到给最后一个小朋友 n 颗糖果。
然后,我们再回到队伍的起点,给第一个小朋友 n + 1 颗糖果,第二个小朋友 n + 2 颗,依此类推,直到给最后一个小朋友 2 * n 颗糖果。
重复上述过程(每次都比上一次多给出一颗糖果,当到达队伍终点后再次从队伍起点开始),直到我们分完所有的糖果。注意,就算我们手中的剩下糖果数不够(不比前一次发出的糖果多),这些糖果也会全部发给当前的小朋友。
返回一个长度为 num_people、元素之和为 candies 的数组,以表示糖果的最终分发情况(即 ans[i] 表示第 i 个小朋友分到的糖果数)。
示例 1:
输入:candies = 7, num_people = 4 输出:[1,2,3,1] 解释: 第一次,ans[0] += 1,数组变为 [1,0,0,0]。 第二次,ans[1] += 2,数组变为 [1,2,0,0]。 第三次,ans[2] += 3,数组变为 [1,2,3,0]。 第四次,ans[3] += 1(因为此时只剩下 1 颗糖果),最终数组变为 [1,2,3,1]。
示例 2:
输入:candies = 10, num_people = 3 输出:[5,2,3] 解释: 第一次,ans[0] += 1,数组变为 [1,0,0]。 第二次,ans[1] += 2,数组变为 [1,2,0]。 第三次,ans[2] += 3,数组变为 [1,2,3]。 第四次,ans[0] += 4,最终数组变为 [5,2,3]。
提示:
1 <= candies <= 10^91 <= num_people <= 1000
解法
Python3
Java
class Solution {
public int[] distributeCandies(int candies, int num_people) {
int[] res = new int[num_people];
for (int i = 0, cur = 1; candies > 0; ++i, ++cur) {
if (i == num_people) {
i = 0;
}
if (candies >= cur) {
res[i] += cur;
candies -= cur;
} else {
res[i] += candies;
candies = 0;
}
}
return res;
}
}
…
1104. 二叉树寻路
English Version
题目描述
在一棵无限的二叉树上,每个节点都有两个子节点,树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示,在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。
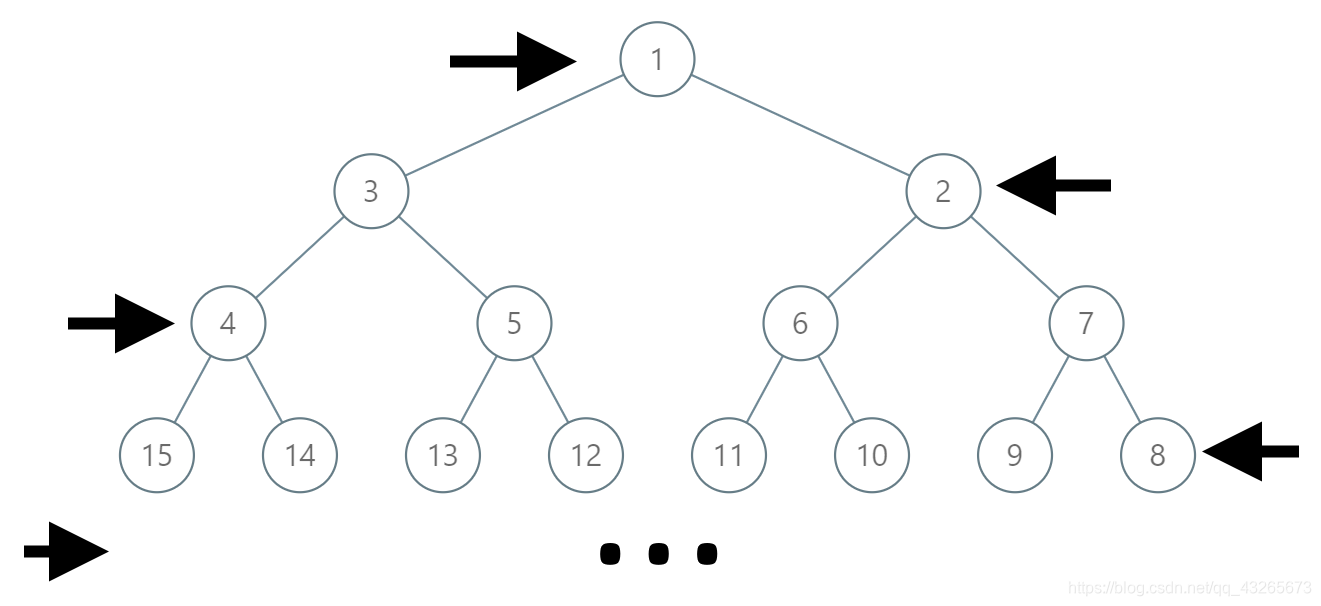给你树上某一个节点的标号 label,请你返回从根节点到该标号为 label 节点的路径,该路径是由途经的节点标号所组成的。
示例 1:
输入:label = 14 输出:[1,3,4,14]
示例 2:
输入:label = 26 输出:[1,2,6,10,26]
提示:
1 <= label <= 10^6
解法
Python3
Java
class Solution {
public List<Integer> pathInZigZagTree(int label) {
List<Integer> res = new ArrayList<>();
int n = Integer.highestOneBit(label);
while (label > 0) {
res.add(label);
int pos = ((n << 1) - 1 - label) >> 1;
label = (n >> 1) + pos;
n >>= 1;
}
Collections.reverse(res);
return res;
}
}
…
1108. IP 地址无效化
English Version
题目描述
给你一个有效的 IPv4 地址 address,返回这个 IP 地址的无效化版本。
所谓无效化 IP 地址,其实就是用 "[.]" 代替了每个 "."。
示例 1:
输入:address = "1.1.1.1" 输出:"1[.]1[.]1[.]1"
示例 2:
输入:address = "255.100.50.0" 输出:"255[.]100[.]50[.]0"
提示:
- 给出的
address是一个有效的 IPv4 地址
解法
Python3
Java
class Solution {
public String defangIPaddr(String address) {
return address.replace(".", "[.]");
}
}
…
1109. 航班预订统计
English Version
题目描述
这里有 n 个航班,它们分别从 1 到 n 进行编号。
我们这儿有一份航班预订表,表中第 i 条预订记录 bookings[i] = [i, j, k] 意味着我们在从 i 到 j 的每个航班上预订了 k 个座位。
请你返回一个长度为 n 的数组 answer,按航班编号顺序返回每个航班上预订的座位数。
示例:
输入:bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5 输出:[10,55,45,25,25]
提示:
1 <= bookings.length <= 200001 <= bookings[i][0] <= bookings[i][1] <= n <= 200001 <= bookings[i][2] <= 10000
解法
Python3
Java
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int[] res = new int[n];
for (int[] booking : bookings) {
int b = booking[0] - 1, e = booking[1], k = booking[2];
res[b] += k;
if (e < n) {
res[e] -= k;
}
}
for (int i = 1; i < n; ++i) {
res[i] += res[i - 1];
}
return res;
}
}
…
1110. 删点成林
English Version
题目描述
给出二叉树的根节点 root,树上每个节点都有一个不同的值。
如果节点值在 to_delete 中出现,我们就把该节点从树上删去,最后得到一个森林(一些不相交的树构成的集合)。
返回森林中的每棵树。你可以按任意顺序组织答案。
示例:
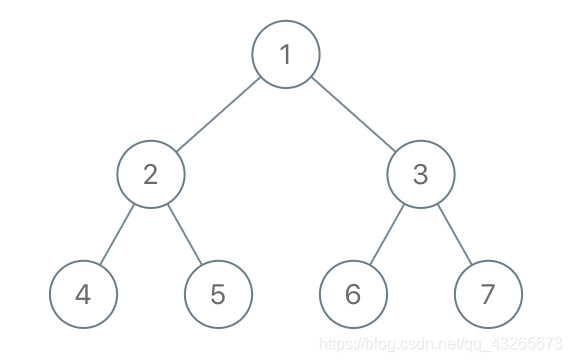输入:root = [1,2,3,4,5,6,7], to_delete = [3,5] 输出:[[1,2,null,4],[6],[7]]
提示:
- 树中的节点数最大为
1000。 - 每个节点都有一个介于
1到1000之间的值,且各不相同。 to_delete.length <= 1000to_delete包含一些从1到1000、各不相同的值。
解法
Python3
Java
class Solution {
public List<TreeNode> delNodes(TreeNode root, int[] to_delete) {
boolean[] del = new boolean[1001];
for (int d : to_delete) {
del[d] = true;
}
List<TreeNode> res = new ArrayList<>();
dfs(root, true, del, res);
return res;
}
private TreeNode dfs(TreeNode root, boolean isRoot, boolean[] del, List<TreeNode> res) {
if (root == null) {
return null;
}
boolean flag = del[root.val];
if (!flag && isRoot) {
res.add(root);
}
root.left = dfs(root.left, flag, del, res);
root.right = dfs(root.right, flag, del, res);
return flag ? null : root;
}
}
…
1111. 有效括号的嵌套深度
English Version
题目描述
有效括号字符串 仅由 "(" 和 ")" 构成,并符合下述几个条件之一:
- 空字符串
- 连接,可以记作
AB(A与B连接),其中A和B都是有效括号字符串 - 嵌套,可以记作
(A),其中A是有效括号字符串
类似地,我们可以定义任意有效括号字符串 s 的 嵌套深度 depth(S):
s为空时,depth("") = 0s为A与B连接时,depth(A + B) = max(depth(A), depth(B)),其中A和B都是有效括号字符串s为嵌套情况,depth("(" + A + ")") = 1 + depth(A),其中 A 是有效括号字符串
例如:"","()()",和 "()(()())" 都是有效括号字符串,嵌套深度分别为 0,1,2,而 ")(" 和 "(()" 都不是有效括号字符串。
给你一个有效括号字符串 seq,将其分成两个不相交的子序列 A 和 B,且 A 和 B 满足有效括号字符串的定义(注意:A.length + B.length = seq.length)。
现在,你需要从中选出 任意 一组有效括号字符串 A 和 B,使 max(depth(A), depth(B)) 的可能取值最小。
返回长度为 seq.length 答案数组 answer ,选择 A 还是 B 的编码规则是:如果 seq[i] 是 A 的一部分,那么 answer[i] = 0。否则,answer[i] = 1。即便有多个满足要求的答案存在,你也只需返回 一个。
示例 1:
输入:seq = "(()())" 输出:[0,1,1,1,1,0]
示例 2:
输入:seq = "()(())()" 输出:[0,0,0,1,1,0,1,1]
提示:
1 <= text.size <= 10000
解法
Python3
Java
class Solution {
public int[] maxDepthAfterSplit(String seq) {
int[] res = new int[seq.length()];
for (int i = 0, cnt = 0; i < res.length; ++i) {
if (seq.charAt(i) == '(') {
res[i] = cnt++ & 1;
} else {
res[i] = --cnt & 1;
}
}
return res;
}
}
…
1114. 按序打印
English Version
题目描述
我们提供了一个类:
public class Foo {
public void one() { print("one"); }
public void two() { print("two"); }
public void three() { print("three"); }
}
三个不同的线程将会共用一个 Foo 实例。
- 线程 A 将会调用
one()方法 - 线程 B 将会调用
two()方法 - 线程 C 将会调用
three()方法
请设计修改程序,以确保 two() 方法在 one() 方法之后被执行,three() 方法在 two() 方法之后被执行。
示例 1:
输入: [1,2,3] 输出: "onetwothree" 解释: 有三个线程会被异步启动。 输入 [1,2,3] 表示线程 A 将会调用 one() 方法,线程 B 将会调用 two() 方法,线程 C 将会调用 three() 方法。 正确的输出是 "onetwothree"。
示例 2:
输入: [1,3,2] 输出: "onetwothree" 解释: 输入 [1,3,2] 表示线程 A 将会调用 one() 方法,线程 B 将会调用 three() 方法,线程 C 将会调用 two() 方法。 正确的输出是 "onetwothree"。
注意:
尽管输入中的数字似乎暗示了顺序,但是我们并不保证线程在操作系统中的调度顺序。
你看到的输入格式主要是为了确保测试的全面性。
解法
Python3
Java
import java.util.concurrent.Semaphore;
class Foo {
private Semaphore twoS = new Semaphore(0);
private Semaphore threeS = new Semaphore(0);
public Foo() {
}
public void first(Runnable printFirst) throws InterruptedException {
printFirst.run();
twoS.release();
}
public void second(Runnable printSecond) throws InterruptedException {
twoS.acquire();
printSecond.run();
threeS.release();
}
public void third(Runnable printThird) throws InterruptedException {
threeS.acquire();
printThird.run();
}
}
…
1115. 交替打印 FooBar
English Version
题目描述
我们提供一个类:
class FooBar {
public void foo() {
for (int i = 0; i < n; i++) {
print("foo");
}
}
public void bar() {
for (int i = 0; i < n; i++) {
print("bar");
}
}
}
两个不同的线程将会共用一个 FooBar 实例。其中一个线程将会调用 foo() 方法,另一个线程将会调用 bar() 方法。
请设计修改程序,以确保 "foobar" 被输出 n 次。
示例 1:
输入: n = 1 输出: "foobar" 解释: 这里有两个线程被异步启动。其中一个调用 foo() 方法, 另一个调用 bar() 方法,"foobar" 将被输出一次。
示例 2:
输入: n = 2 输出: "foobarfoobar" 解释: "foobar" 将被输出两次。
解法
Python3
Java
import java.util.concurrent.locks.Lock;
import java.util.concurrent.locks.ReentrantLock;
class FooBar {
private int n;
private Lock lock;
private volatile Boolean flag;
public FooBar(int n) {
this.n = n;
this.flag = true;
this.lock = new ReentrantLock(true);
}
public void foo(Runnable printFoo) throws InterruptedException {
for (int i = 0; i < n;) {
lock.lock();
if (flag) {
printFoo.run();
flag = false;
i++;
}
lock.unlock();
}
}
public void bar(Runnable printBar) throws InterruptedException {
for (int i = 0; i < n;) {
lock.lock();
if (!flag) {
printBar.run();
flag = true;
i++;
}
lock.unlock();
}
}
}
…
1116. 打印零与奇偶数
English Version
题目描述
假设有这么一个类:
class ZeroEvenOdd {
public ZeroEvenOdd(int n) { ... } // 构造函数
public void zero(printNumber) { ... } // 仅打印出 0
public void even(printNumber) { ... } // 仅打印出 偶数
public void odd(printNumber) { ... } // 仅打印出 奇数
}
相同的一个 ZeroEvenOdd 类实例将会传递给三个不同的线程:
- 线程 A 将调用
zero(),它只输出 0 。 - 线程 B 将调用
even(),它只输出偶数。 - 线程 C 将调用
odd(),它只输出奇数。
每个线程都有一个 printNumber 方法来输出一个整数。请修改给出的代码以输出整数序列 010203040506... ,其中序列的长度必须为 2n。
示例 1:
输入:n = 2 输出:"0102" 说明:三条线程异步执行,其中一个调用 zero(),另一个线程调用 even(),最后一个线程调用odd()。正确的输出为 "0102"。
示例 2:
输入:n = 5 输出:"0102030405"
解法
Python3
Java
class ZeroEvenOdd {
private Semaphore zero_S;
private Semaphore odd_S;
private Semaphore even_S;
private int n;
public ZeroEvenOdd(int n) {
this.n = n;
this.zero_S = new Semaphore(1);
this.odd_S = new Semaphore(0);
this.even_S = new Semaphore(0);
}
// printNumber.accept(x) outputs "x", where x is an integer.
public void zero(IntConsumer printNumber) throws InterruptedException {
for (int i = 1; i <= n; i ++) {
zero_S.acquire(1);
printNumber.accept(0);
if ((i & 1) == 0) {
odd_S.release(1);
} else {
even_S.release(1);
}
}
}
public void even(IntConsumer printNumber) throws InterruptedException {
for (int i = 2; i <= n; i += 2) {
even_S.acquire(1);
printNumber.accept(i);
zero_S.release(1);
}
}
public void odd(IntConsumer printNumber) throws InterruptedException {
for (int i = 1; i <= n; i += 2) {
odd_S.acquire(1);
printNumber.accept(i);
zero_S.release(1);
}
}
}
…
1117. H2O 生成
English Version
题目描述
现在有两种线程,氢 oxygen 和氧 hydrogen,你的目标是组织这两种线程来产生水分子。
存在一个屏障(barrier)使得每个线程必须等候直到一个完整水分子能够被产生出来。
氢和氧线程会被分别给予 releaseHydrogen 和 releaseOxygen 方法来允许它们突破屏障。
这些线程应该三三成组突破屏障并能立即组合产生一个水分子。
你必须保证产生一个水分子所需线程的结合必须发生在下一个水分子产生之前。
换句话说:
- 如果一个氧线程到达屏障时没有氢线程到达,它必须等候直到两个氢线程到达。
- 如果一个氢线程到达屏障时没有其它线程到达,它必须等候直到一个氧线程和另一个氢线程到达。
书写满足这些限制条件的氢、氧线程同步代码。
示例 1:
输入: "HOH" 输出: "HHO" 解释: "HOH" 和 "OHH" 依然都是有效解。
示例 2:
输入: "OOHHHH" 输出: "HHOHHO" 解释: "HOHHHO", "OHHHHO", "HHOHOH", "HOHHOH", "OHHHOH", "HHOOHH", "HOHOHH" 和 "OHHOHH" 依然都是有效解。
限制条件:
- 输入字符串的总长将会是 3n, 1 ≤ n ≤ 50;
- 输入字符串中的 “H” 总数将会是 2n;
- 输入字符串中的 “O” 总数将会是 n。
解法
Python3
Java
class H2O {
private Semaphore h = new Semaphore(2);
private Semaphore o = new Semaphore(0);
public H2O() {
}
public void hydrogen(Runnable releaseHydrogen) throws InterruptedException {
// releaseHydrogen.run() outputs "H". Do not change or remove this line.
h.acquire();
releaseHydrogen.run();
o.release();
}
public void oxygen(Runnable releaseOxygen) throws InterruptedException {
// releaseOxygen.run() outputs "O". Do not change or remove this line.
o.acquire(2);
releaseOxygen.run();
h.release(2);
}
}
…
1122. 数组的相对排序
English Version
题目描述
给你两个数组,arr1 和 arr2,
arr2中的元素各不相同arr2中的每个元素都出现在arr1中
对 arr1 中的元素进行排序,使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。
示例:
输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6] 输出:[2,2,2,1,4,3,3,9,6,7,19]
提示:
arr1.length, arr2.length <= 10000 <= arr1[i], arr2[i] <= 1000arr2中的元素arr2[i]各不相同arr2中的每个元素arr2[i]都出现在arr1中
解法
Python3
Java
class Solution {
public int[] relativeSortArray(int[] arr1, int[] arr2) {
int[] map = new int[1001];
for (int x : arr1) {
++map[x];
}
int i = 0;
for (int x : arr2) {
while (map[x]-- > 0) {
arr1[i++] = x;
}
}
for (int j = 0; j < map.length; ++j) {
while (map[j]-- > 0) {
arr1[i++] = j;
}
}
return arr1;
}
}
…
1123. 最深叶节点的最近公共祖先
English Version
题目描述
给你一个有根节点的二叉树,找到它最深的叶节点的最近公共祖先。
回想一下:
- 叶节点 是二叉树中没有子节点的节点
- 树的根节点的 深度 为
0,如果某一节点的深度为d,那它的子节点的深度就是d+1 - 如果我们假定
A是一组节点S的 最近公共祖先,S中的每个节点都在以A为根节点的子树中,且A的深度达到此条件下可能的最大值。
示例 1:
输入:root = [1,2,3] 输出:[1,2,3]
示例 2:
输入:root = [1,2,3,4] 输出:[4]
示例 3:
输入:root = [1,2,3,4,5] 输出:[2,4,5]
提示:
- 给你的树中将有 1 到 1000 个节点。
- 树中每个节点的值都在 1 到 1000 之间。
解法
Python3
Java
class Solution {
public TreeNode lcaDeepestLeaves(TreeNode root) {
Data data = dfs(root);
return data.root;
}
private Data dfs(TreeNode root) {
if (root == null) {
return new Data(null, 0);
}
Data left = dfs(root.left);
Data right = dfs(root.right);
if (left.d > right.d) return new Data(left.root, 1 + left.d);
if (left.d < right.d) return new Data(right.root, 1 + right.d);
return new Data(root, 1 + left.d);
}
class Data {
TreeNode root;
int d;
public Data(TreeNode root, int d) {
this.root = root;
this.d = d;
}
}
}
…
1124. 表现良好的最长时间段
English Version
题目描述
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9] 输出:3 解释:最长的表现良好时间段是 [9,9,6]。
提示:
1 <= hours.length <= 100000 <= hours[i] <= 16
解法
Python3
Java
class Solution {
public int longestWPI(int[] hours) {
int res = 0;
Map<Integer, Integer> map = new HashMap<>();
int s = 0;
for (int i = 0; i < hours.length; ++i) {
s += hours[i] > 8 ? 1 : -1;
if (s > 0) {
res = i + 1;
} else {
int b = map.getOrDefault(s - 1, -1);
if (b != -1) {
res = Math.max(res, i - b);
}
}
map.putIfAbsent(s, i);
}
return res;
}
}
…
1128. 等价多米诺骨牌对的数量
English Version
题目描述
给你一个由一些多米诺骨牌组成的列表 dominoes。
如果其中某一张多米诺骨牌可以通过旋转 0 度或 180 度得到另一张多米诺骨牌,我们就认为这两张牌是等价的。
形式上,dominoes[i] = [a, b] 和 dominoes[j] = [c, d] 等价的前提是 a==c 且 b==d,或是 a==d 且 b==c。
在 0 <= i < j < dominoes.length 的前提下,找出满足 dominoes[i] 和 dominoes[j] 等价的骨牌对 (i, j) 的数量。
示例:
输入:dominoes = [[1,2],[2,1],[3,4],[5,6]] 输出:1
提示:
1 <= dominoes.length <= 400001 <= dominoes[i][j] <= 9
解法
Python3
Java
class Solution {
public int numEquivDominoPairs(int[][] dominoes) {
Map<Integer, Integer> map = new HashMap<>();
for (int[] d : dominoes) {
int x = d[0] < d[1] ? d[0] * 10 + d[1] : d[1] * 10 + d[0];
map.put(x, map.getOrDefault(x, 0) + 1);
}
int res = 0;
for (int v : map.values()) {
res += v * (v - 1) / 2;
}
return res;
}
}
…
1137. 第 N 个泰波那契数
English Version
题目描述
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4
示例 2:
输入:n = 25 输出:1389537
提示:
0 <= n <= 37- 答案保证是一个 32 位整数,即
answer <= 2^31 - 1。
解法
Python3
Java
class Solution {
public int tribonacci(int n) {
int[] f = new int[]{
0, 1, 1, 2};
for (int i = 4; i <= n; ++i) {
f[i % 4] = f[(i - 1) % 4] + f[(i - 2) % 4] + f[(i - 3) % 4];
}
return f[n % 4];
}
}
…
1138. 字母板上的路径
English Version
题目描述
我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。
在本题里,字母板为board = ["abcde", "fghij", "klmno", "pqrst", "uvwxy", "z"].
我们可以按下面的指令规则行动:
- 如果方格存在,
'U'意味着将我们的位置上移一行; - 如果方格存在,
'D'意味着将我们的位置下移一行; - 如果方格存在,
'L'意味着将我们的位置左移一列; - 如果方格存在,
'R'意味着将我们的位置右移一列; '!'会把在我们当前位置(r, c)的字符board[r][c]添加到答案中。
返回指令序列,用最小的行动次数让答案和目标 target 相同。你可以返回任何达成目标的路径。
示例 1:
输入:target = "leet" 输出:"DDR!UURRR!!DDD!"
示例 2:
输入:target = "code" 输出:"RR!DDRR!UUL!R!"
提示:
1 <= target.length <= 100target仅含有小写英文字母。
解法
Python3
Java
class Solution {
public String alphabetBoardPath(String target) {
StringBuilder sb = new StringBuilder();
int x = 0, y = 0;
for (char c : target.toCharArray()) {
int dx = (c - 'a') / 5;
int dy = (c - 'a') % 5;
if (dy < y) {
int n = y - dy;
while (n-- > 0) {
sb.append('L');
}
}
if (dx > x) {
int n = dx - x;
while (n-- > 0) {
sb.append('D');
}
}
if (dx < x) {
int n = x - dx;
while (n-- > 0) {
sb.append('U');
}
}
if (dy > y) {
int n = dy - y;
while (n-- > 0) {
sb.append('R');
}
}
sb.append('!');
x = dx;
y = dy;
}
return sb.toString();
}
}
…
1139. 最大的以 1 为边界的正方形
English Version
题目描述
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]] 输出:9
示例 2:
输入:grid = [[1,1,0,0]] 输出:1
提示:
1 <= grid.length <= 1001 <= grid[0].length <= 100grid[i][j]为0或1
解法
Python3
Java
class Solution {
public int largest1BorderedSquare(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] down = new int[m][n];
int[][] right = new int[m][n];
for (int i = m - 1; i >= 0; --i) {
for (int j = n - 1; j >= 0; --j) {
if (grid[i][j] == 1) {
down[i][j] += i + 1 < m ? down[i + 1][j] + 1 : 1;
right[i][j] += j + 1 < n ? right[i][j + 1] + 1 : 1;
}
}
}
for (int len = Math.min(m, n); len > 0; --len) {
for (int i = 0; i <= m - len; ++i) {
for (int j = 0; j <= n - len; ++j) {
if (down[i][j] >= len && right[i][j] >= len && right[i + len - 1][j] >= len && down[i][j + len - 1] >= len) {
return len * len;
}
}
}
}
return 0;
}
}
…
1140. 石子游戏 II
English Version
题目描述
亚历克斯和李继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整数颗石子 piles[i]。游戏以谁手中的石子最多来决出胜负。
亚历克斯和李轮流进行,亚历克斯先开始。最初,M = 1。
在每个玩家的回合中,该玩家可以拿走剩下的 前 X 堆的所有石子,其中 1 <= X <= 2M。然后,令 M = max(M, X)。
游戏一直持续到所有石子都被拿走。
假设亚历克斯和李都发挥出最佳水平,返回亚历克斯可以得到的最大数量的石头。
示例:
输入:piles = [2,7,9,4,4] 输出:10 解释: 如果亚历克斯在开始时拿走一堆石子,李拿走两堆,接着亚历克斯也拿走两堆。在这种情况下,亚历克斯可以拿到 2 + 4 + 4 = 10 颗石子。 如果亚历克斯在开始时拿走两堆石子,那么李就可以拿走剩下全部三堆石子。在这种情况下,亚历克斯可以拿到 2 + 7 = 9 颗石子。 所以我们返回更大的 10。
提示:
1 <= piles.length <= 1001 <= piles[i] <= 10 ^ 4
解法
Python3
Java
class Solution {
public int stoneGameII(int[] piles) {
Map<Integer, Integer> map = new HashMap<>();
int total = Arrays.stream(piles).sum();
return (total + dfs(0, 1, piles, map)) >> 1;
}
private int dfs(int s, int M, int[] piles, Map<Integer, Integer> map) {
if (s >= piles.length) {
return 0;
}
int key = s << 8 | M;
if (map.containsKey(key)) {
return map.get(key);
}
if (s + 2 * M >= piles.length) {
int res = 0;
for (int i = s; i < piles.length; ++i) {
res += piles[i];
}
return res;
}
int best = Integer.MIN_VALUE;
int cur = 0;
for (int x = 1; x <= 2 * M && s + x - 1 < piles.length; ++x) {
cur += piles[s + x - 1];
best = Math.max(best, cur - dfs(s + x, Math.max(x, M), piles, map));
}
map.put(key, best);
return best;
}
}
…
1144. 递减元素使数组呈锯齿状
English Version
题目描述
给你一个整数数组 nums,每次 操作 会从中选择一个元素并 将该元素的值减少 1。
如果符合下列情况之一,则数组 A 就是 锯齿数组:
- 每个偶数索引对应的元素都大于相邻的元素,即
A[0] > A[1] < A[2] > A[3] < A[4] > ... - 或者,每个奇数索引对应的元素都大于相邻的元素,即
A[0] < A[1] > A[2] < A[3] > A[4] < ...
返回将数组 nums 转换为锯齿数组所需的最小操作次数。
示例 1:
输入:nums = [1,2,3] 输出:2 解释:我们可以把 2 递减到 0,或把 3 递减到 1。
示例 2:
输入:nums = [9,6,1,6,2] 输出:4
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1000
解法
Python3
Java
class Solution {
public int movesToMakeZigzag(int[] nums) {
int[] res = new int[2];
for (int i = 0, n = nums.length; i < n; ++i) {
int left = i > 0 ? nums[i - 1] : Integer.MAX_VALUE;
int right = i + 1 < n ? nums[i + 1] : Integer.MAX_VALUE;
res[i & 1] += Math.max(0, nums[i] - (Math.min(left, right) - 1));
}
return Math.min(res[0], res[1]);
}
}
…
1147. 段式回文
English Version
题目描述
段式回文 其实与 一般回文 类似,只不过是最小的单位是 一段字符 而不是 单个字母。
举个例子,对于一般回文 "abcba" 是回文,而 "volvo" 不是,但如果我们把 "volvo" 分为 "vo"、"l"、"vo" 三段,则可以认为 “(vo)(l)(vo)” 是段式回文(分为 3 段)。
给你一个字符串 text,在确保它满足段式回文的前提下,请你返回 段 的 最大数量 k。
如果段的最大数量为 k,那么存在满足以下条件的 a_1, a_2, ..., a_k:
- 每个
a_i都是一个非空字符串; - 将这些字符串首位相连的结果
a_1 + a_2 + ... + a_k和原始字符串text相同; - 对于所有
1 <= i <= k,都有a_i = a_{k+1 - i}。
示例 1:
输入:text = "ghiabcdefhelloadamhelloabcdefghi" 输出:7 解释:我们可以把字符串拆分成 "(ghi)(abcdef)(hello)(adam)(hello)(abcdef)(ghi)"。
示例 2:
输入:text = "merchant" 输出:1 解释:我们可以把字符串拆分成 "(merchant)"。
示例 3:
输入:text = "antaprezatepzapreanta" 输出:11 解释:我们可以把字符串拆分成 "(a)(nt)(a)(pre)(za)(tpe)(za)(pre)(a)(nt)(a)"。
示例 4:
输入:text = "aaa" 输出:3 解释:我们可以把字符串拆分成 "(a)(a)(a)"。
提示:
text仅由小写英文字符组成。1 <= text.length <= 1000
解法
Python3
Java
class Solution {
public int longestDecomposition(String text) {
char[] cs = text.toCharArray();
int res = 0;
for (int i = 0, j = cs.length - 1; i <= j; ) {
boolean flag = true;
for (int k = 1; i + k - 1 < j - k + 1; ++k) {
if (check(cs, i, j - k + 1, k)) {
res += 2;
i += k;
j -= k;
flag = false;
break;
}
}
if (flag) {
++res;
break;
}
}
return res;
}
private boolean check(char[] cs, int i, int j, int k) {
while (k-- > 0) {
if (cs[i++] != cs[j++]) {
return false;
}
}
return true;
}
}
…
1155. 掷骰子的 N 种方法
English Version
题目描述
这里有 d 个一样的骰子,每个骰子上都有 f 个面,分别标号为 1, 2, ..., f。
我们约定:掷骰子的得到总点数为各骰子面朝上的数字的总和。
如果需要掷出的总点数为 target,请你计算出有多少种不同的组合情况(所有的组合情况总共有 f^d 种),模 10^9 + 7 后返回。
示例 1:
输入:d = 1, f = 6, target = 3 输出:1
示例 2:
输入:d = 2, f = 6, target = 7 输出:6
示例 3:
输入:d = 2, f = 5, target = 10 输出:1
示例 4:
输入:d = 1, f = 2, target = 3 输出:0
示例 5:
输入:d = 30, f = 30, target = 500 输出:222616187
提示:
1 <= d, f <= 301 <= target <= 1000
解法
Python3
Java
class Solution {
public int numRollsToTarget(int d, int f, int target) {
int[][] dp = new int[d + 1][target + 1];
dp[0][0] = 1;
for (int i = 1; i <= d; ++i) {
for (int j = 1; j <= target; ++j) {
// j 大于当前所有骰子的最大和,不可能满足条件
if (j > i * f) {
break;
}
for (int k = 1; k <= f && k <= j; ++k) {
dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % 1000000007;
}
}
}
return dp[d][target];
}
}
…
1171. 从链表中删去总和值为零的连续节点
English Version
题目描述
给你一个链表的头节点 head,请你编写代码,反复删去链表中由 总和 值为 0 的连续节点组成的序列,直到不存在这样的序列为止。
删除完毕后,请你返回最终结果链表的头节点。
你可以返回任何满足题目要求的答案。
(注意,下面示例中的所有序列,都是对 ListNode 对象序列化的表示。)
示例 1:
输入:head = [1,2,-3,3,1] 输出:[3,1] 提示:答案 [1,2,1] 也是正确的。
示例 2:
输入:head = [1,2,3,-3,4] 输出:[1,2,4]
示例 3:
输入:head = [1,2,3,-3,-2] 输出:[1]
提示:
- 给你的链表中可能有
1到1000个节点。 - 对于链表中的每个节点,节点的值:
-1000 <= node.val <= 1000.
解法
Python3
Java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode removeZeroSumSublists(ListNode head) {
Map<Integer, ListNode> map = new HashMap<>();
boolean isZeroSum = true;
while (isZeroSum) {
isZeroSum = false;
int sum = 0;
ListNode temp = head;
while (temp != null) {
sum += temp.val;
if (sum == 0) {
head = temp.next;
map.clear();
isZeroSum = true;
break;
} else if (map.containsKey(sum)) {
map.get(sum).next = temp.next;
map.clear();
isZeroSum = true;
break;
}
map.put(sum, temp);
temp = temp.next;
}
}
return head;
}
}
…
1184. 公交站间的距离
English Version
题目描述
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例 1:
输入:distance = [1,2,3,4], start = 0, destination = 1 输出:1 解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
示例 2:
输入:distance = [1,2,3,4], start = 0, destination = 2 输出:3 解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
示例 3:
输入:distance = [1,2,3,4], start = 0, destination = 3 输出:4 解释:公交站 0 和 3 之间的距离是 6 或 4,最小值是 4。
提示:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
解法
Python3
Java
class Solution {
public static int distanceBetweenBusStops(int[] distance, int start, int destination) {
int length = 0;
for (int i : distance) {
length += i;
}
int min = Math.min(start, destination);
int max = Math.max(start, destination);
int length2 = 0;
for (int i = min; i < max; i++) {
length2 += distance[i];
}
return Math.min(length - length2, length2);
}
}
…
1185. 一周中的第几天
English Version
题目描述
给你一个日期,请你设计一个算法来判断它是对应一周中的哪一天。
输入为三个整数:day、month 和 year,分别表示日、月、年。
您返回的结果必须是这几个值中的一个 {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"}。
示例 1:
输入:day = 31, month = 8, year = 2019 输出:"Saturday"
示例 2:
输入:day = 18, month = 7, year = 1999 输出:"Sunday"
示例 3:
输入:day = 15, month = 8, year = 1993 输出:"Sunday"
提示:
- 给出的日期一定是在
1971到2100年之间的有效日期。
解法
Python3
Java
import java.util.Calendar;
class Solution {
private static final String[] WEEK = {
"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
public static String dayOfTheWeek(int day, int month, int year) {
Calendar calendar = Calendar.getInstance();
calendar.set(year, month - 1, day);
return WEEK[calendar.get(Calendar.DAY_OF_WEEK) - 1];
}
}
…
1195. 交替打印字符串
English Version
题目描述
编写一个可以从 1 到 n 输出代表这个数字的字符串的程序,但是:
- 如果这个数字可以被 3 整除,输出 "fizz"。
- 如果这个数字可以被 5 整除,输出 "buzz"。
- 如果这个数字可以同时被 3 和 5 整除,输出 "fizzbuzz"。
例如,当 n = 15,输出: 1, 2, fizz, 4, buzz, fizz, 7, 8, fizz, buzz, 11, fizz, 13, 14, fizzbuzz。
假设有这么一个类:
class FizzBuzz {
public FizzBuzz(int n) { ... } // constructor
public void fizz(printFizz) { ... } // only output "fizz"
public void buzz(printBuzz) { ... } // only output "buzz"
public void fizzbuzz(printFizzBuzz) { ... } // only output "fizzbuzz"
public void number(printNumber) { ... } // only output the numbers
}
请你实现一个有四个线程的多线程版 FizzBuzz, 同一个 FizzBuzz 实例会被如下四个线程使用:
- 线程A将调用
fizz()来判断是否能被 3 整除,如果可以,则输出fizz。 - 线程B将调用
buzz()来判断是否能被 5 整除,如果可以,则输出buzz。 - 线程C将调用
fizzbuzz()来判断是否同时能被 3 和 5 整除,如果可以,则输出fizzbuzz。 - 线程D将调用
number()来实现输出既不能被 3 整除也不能被 5 整除的数字。
解法
Python3
Java
class FizzBuzz {
private int n;
public FizzBuzz(int n) {
this.n = n;
}
private Semaphore fSema = new Semaphore(0);
private Semaphore bSema = new Semaphore(0);
private Semaphore fbSema = new Semaphore(0);
private Semaphore nSema = new Semaphore(1);
// printFizz.run() outputs "fizz".
public void fizz(Runnable printFizz) throws InterruptedException {
for (int i = 3; i <= n; i = i + 3) {
if (i % 5 != 0) {
fSema.acquire();
printFizz.run();
nSema.release();
}
}
}
// printBuzz.run() outputs "buzz".
public void buzz(Runnable printBuzz) throws InterruptedException {
for (int i = 5; i <= n; i = i + 5) {
if (i % 3 != 0) {
bSema.acquire();
printBuzz.run();
nSema.release();
}
}
}
// printFizzBuzz.run() outputs "fizzbuzz".
public void fizzbuzz(Runnable printFizzBuzz) throws InterruptedException {
for (int i = 15; i <= n; i = i + 15) {
fbSema.acquire();
printFizzBuzz.run();
nSema.release();
}
}
// printNumber.accept(x) outputs "x", where x is an integer.
public void number(IntConsumer printNumber) throws InterruptedException {
for (int i = 1; i <= n; i++) {
nSema.acquire();
if (i % 3 == 0 && i % 5 == 0) {
fbSema.release();
} else if (i % 3 == 0) {
fSema.release();
} else if (i % 5 == 0) {
bSema.release();
} else {
printNumber.accept(i);
nSema.release();
}
}
}
}
C++
class FizzBuzz {
private:
std::mutex mtx;
atomic<int> index;
int n;
// 这里主要运用到了C++11中的RAII锁(lock_guard)的知识。
// 需要强调的一点是,在进入循环后,要时刻不忘加入index <= n的逻辑
public:
FizzBuzz(int n) {
this->n = n;
index = 1;
}
void fizz(function<void()> printFizz) {
while (index <= n) {
std::lock_guard<std::mutex> lk(mtx);
if (0 == index % 3 && 0 != index % 5 && index <= n) {
printFizz();
index++;
}
}
}
void buzz(function<void()> printBuzz) {
while (index <= n) {
std::lock_guard<std::mutex> lk(mtx);
if (0 == index % 5 && 0 != index % 3 && index <= n){
printBuzz();
index++;
}
}
}
void fizzbuzz(function<void()> printFizzBuzz) {
while (index <= n) {
std::lock_guard<std::mutex> lk(mtx);
if (0 == index % 15 && index <= n) {
printFizzBuzz();
index++;
}
}
}
void number(function<void(int)> printNumber) {
while (index <= n) {
std::lock_guard<std::mutex> lk(mtx);
if (0 != index % 3 && 0 != index % 5 && index <= n) {
printNumber(index);
index++;
}
}
}
};
…
1287. 有序数组中出现次数超过 25%的元素
English Version
题目描述
给你一个非递减的 有序 整数数组,已知这个数组中恰好有一个整数,它的出现次数超过数组元素总数的 25%。
请你找到并返回这个整数
示例:
输入:arr = [1,2,2,6,6,6,6,7,10] 输出:6
提示:
1 <= arr.length <= 10^40 <= arr[i] <= 10^5
解法
Python3
Java
class Solution {
public int findSpecialInteger(int[] arr) {
int total = arr.length;
for (int i = 0; i < total; ++i) {
if (arr[i] == arr[i + (total >> 2)]) {
return arr[i];
}
}
return 0;
}
}
…
1290. 二进制链表转整数
English Version
题目描述
给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。
请你返回该链表所表示数字的 十进制值 。
示例 1:
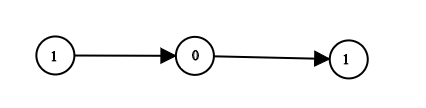输入:head = [1,0,1] 输出:5 解释:二进制数 (101) 转化为十进制数 (5)
示例 2:
输入:head = [0] 输出:0
示例 3:
输入:head = [1] 输出:1
示例 4:
输入:head = [1,0,0,1,0,0,1,1,1,0,0,0,0,0,0] 输出:18880
示例 5:
输入:head = [0,0] 输出:0
提示:
- 链表不为空。
- 链表的结点总数不超过
30。 - 每个结点的值不是
0就是1。
解法
Python3
Java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int getDecimalValue(ListNode head) {
int sum = 0;
StringBuilder sb = new StringBuilder("0");
while (head != null) {
sum += head.val;
if (sum != 0) {
sb.append(head.val);
}
head = head.next;
}
return Integer.valueOf(sb.toString(), 2);
}
}
…
1295. 统计位数为偶数的数字
English Version
题目描述
给你一个整数数组 nums,请你返回其中位数为 偶数 的数字的个数。
示例 1:
输入:nums = [12,345,2,6,7896] 输出:2 解释: 12 是 2 位数字(位数为偶数) 345 是 3 位数字(位数为奇数) 2 是 1 位数字(位数为奇数) 6 是 1 位数字 位数为奇数) 7896 是 4 位数字(位数为偶数) 因此只有 12 和 7896 是位数为偶数的数字
示例 2:
输入:nums = [555,901,482,1771] 输出:1 解释: 只有 1771 是位数为偶数的数字。
提示:
1 <= nums.length <= 5001 <= nums[i] <= 10^5
解法
首先将数组元素转换为字符串,判断字符串长度是否为偶数即可。
Python3
class Solution:
def findNumbers(self, nums: List[int]) -> int:
res = 0
for num in nums:
res += (len(str(num)) & 1) == 0
return res
Java
class Solution {
public int findNumbers(int[] nums) {
int res = 0;
for (int num : nums) {
res += (String.valueOf(num).length() & 1) == 0 ? 1 : 0;
}
return res;
}
}
…
1346. 检查整数及其两倍数是否存在
English Version
题目描述
给你一个整数数组 arr,请你检查是否存在两个整数 N 和 M,满足 N 是 M 的两倍(即,N = 2 * M)。
更正式地,检查是否存在两个下标 i 和 j 满足:
i != j0 <= i, j < arr.lengtharr[i] == 2 * arr[j]
示例 1:
输入:arr = [10,2,5,3] 输出:true 解释:N= 10是 M= 5 的两倍,即10 = 2 * 5 。
示例 2:
输入:arr = [7,1,14,11] 输出:true 解释:N= 14是 M= 7 的两倍,即14 = 2 * 7。
示例 3:
输入:arr = [3,1,7,11] 输出:false 解释:在该情况下不存在 N 和 M 满足 N = 2 * M 。
提示:
2 <= arr.length <= 500-10^3 <= arr[i] <= 10^3
解法
Python3
Java
import java.util.*;
class Solution {
public boolean checkIfExist(int[] arr) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
map.put(arr[i], i);
}
for (int i = 0; i < arr.length; i++) {
if (map.containsKey(arr[i] * 2) && i != map.get(arr[i] * 2))
return true;
}
return false;
}
}
…
1347. 制造字母异位词的最小步骤数
English Version
题目描述
给你两个长度相等的字符串 s 和 t。每一个步骤中,你可以选择将 t 中的 任一字符 替换为 另一个字符。
返回使 t 成为 s 的字母异位词的最小步骤数。
字母异位词 指字母相同,但排列不同的字符串。
示例 1:
输出:s = "bab", t = "aba" 输出:1 提示:用 'b' 替换 t 中的第一个 'a',t = "bba" 是 s 的一个字母异位词。
示例 2:
输出:s = "leetcode", t = "practice" 输出:5 提示:用合适的字符替换 t 中的 'p', 'r', 'a', 'i' 和 'c',使 t 变成 s 的字母异位词。
示例 3:
输出:s = "anagram", t = "mangaar" 输出:0 提示:"anagram" 和 "mangaar" 本身就是一组字母异位词。
示例 4:
输出:s = "xxyyzz", t = "xxyyzz" 输出:0
示例 5:
输出:s = "friend", t = "family" 输出:4
提示:
1 <= s.length <= 50000s.length == t.lengths和t只包含小写英文字母
解法
Python3
Java
import java.util.*;
class Solution {
public int minSteps(String s, String t) {
Map<Character, Integer> map = new HashMap<>();
for (char c : t.toCharArray()) {
if (map.containsKey(c)) {
map.put(c, map.get(c) + 1);
} else map.put(c, 1);
}
int res = 0;
for (char c : s.toCharArray()) {
if (map.containsKey(c) && map.get(c) > 0) {
map.put(c, map.get(c) - 1);
} else res ++;
}
return res;
}
}
…
1380. 矩阵中的幸运数
English Version
题目描述
给你一个 m * n 的矩阵,矩阵中的数字 各不相同 。请你按 任意 顺序返回矩阵中的所有幸运数。
幸运数是指矩阵中满足同时下列两个条件的元素:
- 在同一行的所有元素中最小
- 在同一列的所有元素中最大
示例 1:
输入:matrix = [[3,7,8],[9,11,13],[15,16,17]] 输出:[15] 解释:15 是唯一的幸运数,因为它是其所在行中的最小值,也是所在列中的最大值。
示例 2:
输入:matrix = [[1,10,4,2],[9,3,8,7],[15,16,17,12]] 输出:[12] 解释:12 是唯一的幸运数,因为它是其所在行中的最小值,也是所在列中的最大值。
示例 3:
输入:matrix = [[7,8],[1,2]] 输出:[7]
提示:
m == mat.lengthn == mat[i].length1 <= n, m <= 501 <= matrix[i][j] <= 10^5- 矩阵中的所有元素都是不同的
解法
取行最小值与列最大值的交集即可。
Python3
class Solution:
def luckyNumbers (self, matrix: List[List[int]]) -> List[int]:
row_min = {
min(rows) for rows in matrix}
col_max = {
max(cols) for cols in zip(*matrix)}
return [e for e in row_min if e in col_max]
Java
class Solution {
public List<Integer> luckyNumbers (int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
Set<Integer> rowMin = new HashSet<>();
List<Integer> res = new ArrayList<>();
for (int i = 0; i < m; ++i) {
int min = Integer.MAX_VALUE;
for (int j = 0; j < n; ++j) {
min = Math.min(min, matrix[i][j]);
}
rowMin.add(min);
}
for (int j = 0; j < n; ++j) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < m; ++i) {
max = Math.max(max, matrix[i][j]);
}
if (rowMin.contains(max)) {
res.add(max);
}
}
return res;
}
}
…
1476. 子矩形查询
English Version
题目描述
请你实现一个类 SubrectangleQueries ,它的构造函数的参数是一个 rows x cols 的矩形(这里用整数矩阵表示),并支持以下两种操作:
1. updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)
- 用
newValue更新以(row1,col1)为左上角且以(row2,col2)为右下角的子矩形。
2. getValue(int row, int col)
- 返回矩形中坐标
(row,col)的当前值。
示例 1:
输入: ["SubrectangleQueries","getValue","updateSubrectangle","getValue","getValue","updateSubrectangle","getValue","getValue"] [[[[1,2,1],[4,3,4],[3,2,1],[1,1,1]]],[0,2],[0,0,3,2,5],[0,2],[3,1],[3,0,3,2,10],[3,1],[0,2]] 输出: [null,1,null,5,5,null,10,5] 解释: SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,2,1],[4,3,4],[3,2,1],[1,1,1]]); // 初始的 (4x3) 矩形如下: // 1 2 1 // 4 3 4 // 3 2 1 // 1 1 1 subrectangleQueries.getValue(0, 2); // 返回 1 subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5); // 此次更新后矩形变为: // 5 5 5 // 5 5 5 // 5 5 5 // 5 5 5 subrectangleQueries.getValue(0, 2); // 返回 5 subrectangleQueries.getValue(3, 1); // 返回 5 subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10); // 此次更新后矩形变为: // 5 5 5 // 5 5 5 // 5 5 5 // 10 10 10 subrectangleQueries.getValue(3, 1); // 返回 10 subrectangleQueries.getValue(0, 2); // 返回 5
示例 2:
输入: ["SubrectangleQueries","getValue","updateSubrectangle","getValue","getValue","updateSubrectangle","getValue"] [[[[1,1,1],[2,2,2],[3,3,3]]],[0,0],[0,0,2,2,100],[0,0],[2,2],[1,1,2,2,20],[2,2]] 输出: [null,1,null,100,100,null,20] 解释: SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,1,1],[2,2,2],[3,3,3]]); subrectangleQueries.getValue(0, 0); // 返回 1 subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100); subrectangleQueries.getValue(0, 0); // 返回 100 subrectangleQueries.getValue(2, 2); // 返回 100 subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20); subrectangleQueries.getValue(2, 2); // 返回 20
提示:
- 最多有
500次updateSubrectangle和getValue操作。 1 <= rows, cols <= 100rows == rectangle.lengthcols == rectangle[i].length0 <= row1 <= row2 < rows0 <= col1 <= col2 < cols1 <= newValue, rectangle[i][j] <= 10^90 <= row < rows0 <= col < cols
解法
Python3
Java
class SubrectangleQueries {
int[][] matrix;
public SubrectangleQueries(int[][] rectangle) {
matrix = new int[rectangle.length][rectangle[0].length];
for (int i = 0; i < rectangle.length; i++) {
for (int j = 0; j < rectangle[0].length; j++) {
matrix[i][j] = rectangle[i][j];
}
}
}
public void updateSubrectangle(int row1, int col1, int row2, int col2, int newValue) {
if (row1 > row2 || col1 > col2) {
return;
}
for (int i = row1; i <= row2; i++) {
for (int j = col1; j <= col2; j++) {
matrix[i][j] = newValue;
}
}
}
public int getValue(int row, int col) {
return matrix[row][col];
}
}
/**
* Your SubrectangleQueries object will be instantiated and called as such:
* SubrectangleQueries obj = new SubrectangleQueries(rectangle);
* obj.updateSubrectangle(row1,col1,row2,col2,newValue);
* int param_2 = obj.getValue(row,col);
*/
…
1535. 找出数组游戏的赢家
English Version
题目描述
给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。
每回合游戏都在数组的前两个元素(即 arr[0] 和 arr[1] )之间进行。比较 arr[0] 与 arr[1] 的大小,较大的整数将会取得这一回合的胜利并保留在位置 0 ,较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时,游戏结束,该整数就是比赛的 赢家 。
返回赢得比赛的整数。
题目数据 保证 游戏存在赢家。
示例 1:
输入:arr = [2,1,3,5,4,6,7], k = 2 输出:5 解释:一起看一下本场游戏每回合的情况:  因此将进行 4 回合比赛,其中 5 是赢家,因为它连胜 2 回合。
示例 2:
输入:arr = [3,2,1], k = 10 输出:3 解释:3 将会在前 10 个回合中连续获胜。
示例 3:
输入:arr = [1,9,8,2,3,7,6,4,5], k = 7 输出:9
示例 4:
输入:arr = [1,11,22,33,44,55,66,77,88,99], k = 1000000000 输出:99
提示:
2 <= arr.length <= 10^51 <= arr[i] <= 10^6arr所含的整数 各不相同 。1 <= k <= 10^9
解法
Python3
Java
class Solution {
public int getWinner(int[] arr, int k) {
int time = 0, max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (max > arr[i]) {
time++;
} else {
time = 1;
max = arr[i];
}
if (time >= k) {
return max;
}
}
return max;
}
}
…
1537. 最大得分
English Version
题目描述
你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。
一条 合法路径 定义如下:
- 选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。
- 从左到右遍历当前数组。
- 如果你遇到了
nums1和nums2中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在合法路径中重复数字只会被统计一次)。
得分定义为合法路径中不同数字的和。
请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例 1:
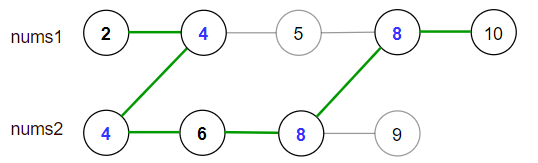输入:nums1 = [2,4,5,8,10], nums2 = [4,6,8,9] 输出:30 解释:合法路径包括: [2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],(从 nums1 开始遍历) [4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] (从 nums2 开始遍历) 最大得分为上图中的绿色路径 [2,4,6,8,10] 。
示例 2:
输入:nums1 = [1,3,5,7,9], nums2 = [3,5,100] 输出:109 解释:最大得分由路径 [1,3,5,100] 得到。
示例 3:
输入:nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10] 输出:40 解释:nums1 和 nums2 之间无相同数字。 最大得分由路径 [6,7,8,9,10] 得到。
示例 4:
输入:nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12] 输出:61
提示:
1 <= nums1.length <= 10^51 <= nums2.length <= 10^51 <= nums1[i], nums2[i] <= 10^7nums1和nums2都是严格递增的数组。
解法
Python3
Java
class Solution {
final int MOD = (int) (1e9 + 7);
public int maxSum(int[] nums1, int[] nums2) {
Set<Integer> set1 = Arrays.stream(nums1).boxed().collect(Collectors.toSet());
Set<Integer> set2 = Arrays.stream(nums2).boxed().collect(Collectors.toSet());
set1.retainAll(set2);
if (set1.isEmpty()) {
return (int) (Math.max(sum(nums1, 0, nums1.length - 1), sum(nums2, 0, nums2.length - 1))
% MOD);
}
long res = 0;
List<Integer> list = set1.stream().sorted(Comparator.naturalOrder())
.collect(Collectors.toList());
int start1 = 0, start2 = 0, end1 = 0, end2 = 0;
for (int common : list) {
// 2 个数组同时到达 set
while (nums1[end1] != common) {
end1++;
}
while (nums2[end2] != common) {
end2++;
}
// max
res += Math.max(sum(nums1, start1, end1), sum(nums2, start2, end2));
start1 = end1 + 1;
start2 = end2 + 1;
}
res += Math.max(sum(nums1, end1 + 1, nums1.length - 1),
sum(nums2, end2 + 1, nums2.length - 1));
res %= MOD;
return (int) res;
}
private long sum(int[] n, int l, int r) {
long res = 0;
while (l <= r) {
res += n[l++];
}
return res;
}
}
…
1541. 平衡括号字符串的最少插入次数
English Version
题目描述
给你一个括号字符串 s ,它只包含字符 '(' 和 ')' 。一个括号字符串被称为平衡的当它满足:
- 任何左括号
'('必须对应两个连续的右括号'))'。 - 左括号
'('必须在对应的连续两个右括号'))'之前。
比方说 "())", "())(())))" 和 "(())())))" 都是平衡的, ")()", "()))" 和 "(()))" 都是不平衡的。
你可以在任意位置插入字符 '(' 和 ')' 使字符串平衡。
请你返回让 s 平衡的最少插入次数。
示例 1:
输入:s = "(()))" 输出:1 解释:第二个左括号有与之匹配的两个右括号,但是第一个左括号只有一个右括号。我们需要在字符串结尾额外增加一个 ')' 使字符串变成平衡字符串 "(())))" 。
示例 2:
输入:s = "())" 输出:0 解释:字符串已经平衡了。
示例 3:
输入:s = "))())("
输出:3
解释:添加 '(' 去匹配最开头的 '))' ,然后添加 '))' 去匹配最后一个 '(' 。
示例 4:
输入:s = "(((((("
输出:12
解释:添加 12 个 ')' 得到平衡字符串。
示例 5:
输入:s = ")))))))"
输出:5
解释:在字符串开头添加 4 个 '(' 并在结尾添加 1 个 ')' ,字符串变成平衡字符串 "(((())))))))" 。
提示:
1 <= s.length <= 10^5s只包含'('和')'。
解法
Python3
Java
class Solution {
public int minInsertions(String s) {
int left = 0;
int res = 0;
char[] chars = s.toCharArray();
for (int i = 0; i < chars.length;) {
if (chars[i] == '(') {
left++;
i++;
} else {
// 连续2个 )
if (i < chars.length - 1 && chars[i + 1] == ')') {
if (left > 0) {
left--;
} else {
res++;
}
i += 2;
} else {
if (left > 0) {
left--;
res++;
} else {
res += 2;
}
i++;
}
}
}
if (left > 0) {
res += 2 * left;
}
return res;
}
}
…
1544. 整理字符串
English Version
题目描述
给你一个由大小写英文字母组成的字符串 s 。
一个整理好的字符串中,两个相邻字符 s[i] 和 s[i + 1] 不会同时满足下述条件:
0 <= i <= s.length - 2s[i]是小写字符,但s[i + 1]是相同的大写字符;反之亦然 。
请你将字符串整理好,每次你都可以从字符串中选出满足上述条件的 两个相邻 字符并删除,直到字符串整理好为止。
请返回整理好的 字符串 。题目保证在给出的约束条件下,测试样例对应的答案是唯一的。
注意:空字符串也属于整理好的字符串,尽管其中没有任何字符。
示例 1:
输入:s = "leEeetcode" 输出:"leetcode" 解释:无论你第一次选的是 i = 1 还是 i = 2,都会使 "leEeetcode" 缩减为 "leetcode" 。
示例 2:
输入:s = "abBAcC" 输出:"" 解释:存在多种不同情况,但所有的情况都会导致相同的结果。例如: "abBAcC" --> "aAcC" --> "cC" --> "" "abBAcC" --> "abBA" --> "aA" --> ""
示例 3:
输入:s = "s" 输出:"s"
提示:
1 <= s.length <= 100s只包含小写和大写英文字母
解法
Python3
Java
class Solution {
public String makeGood(String s) {
return help(s);
}
private String help(String s) {
if (s == null || s.length() == 0 || s.length() == 1) {
return s;
}
char[] chars = s.toCharArray();
for (int i = 1; i < chars.length; i++) {
if (Math.abs(chars[i] - chars[i - 1]) == Math.abs('A' - 'a')) {
return help(newString(chars, i));
}
}
return s;
}
private String newString(char[] chars, int i) {
StringBuilder tmp = new StringBuilder();
for (int j = 0; j < chars.length; j++) {
if (j != i && j != i - 1) {
tmp.append(chars[j]);
}
}
return tmp.toString();
}
}
…
1545. 找出第 N 个二进制字符串中的第 K 位
English Version
题目描述
给你两个正整数 n 和 k,二进制字符串 Sn 的形成规则如下:
S1 = "0"- 当
i > 1时,Si = Si-1 + "1" + reverse(invert(Si-1))
其中 + 表示串联操作,reverse(x) 返回反转 x 后得到的字符串,而 invert(x) 则会翻转 x 中的每一位(0 变为 1,而 1 变为 0)
例如,符合上述描述的序列的前 4 个字符串依次是:
S1 = "0"S2 = "011"S3 = "0111001"S4 = "011100110110001"
请你返回 Sn 的 第 k 位字符 ,题目数据保证 k 一定在 Sn 长度范围以内。
示例 1:
输入:n = 3, k = 1 输出:"0" 解释:S3 为 "0111001",其第 1 位为 "0" 。
示例 2:
输入:n = 4, k = 11 输出:"1" 解释:S4 为 "011100110110001",其第 11 位为 "1" 。
示例 3:
输入:n = 1, k = 1 输出:"0"
示例 4:
输入:n = 2, k = 3 输出:"1"
提示:
1 <= n <= 201 <= k <= 2n - 1
解法
Python3
Java
class Solution {
public char findKthBit(int n, int k) {
if (k == 1 || n == 1) {
return '0';
}
Set<Integer> set = new HashSet<>();
int len = calcLength(n, set);
if (set.contains(k)) {
return '1';
}
// 中间,返回1
if (k < len / 2) {
return findKthBit(n - 1, k);
} else {
if (set.contains(len - k)) {
return '1';
}
return r(findKthBit(n - 1, len - k + 1));
}
}
private char r(char b) {
if (b == '0') {
return '1';
}
return '0';
}
private int calcLength(int n, Set<Integer> set) {
if (n == 1) {
return 1;
}
int ans = 2 * calcLength(n - 1, set) + 1;
set.add(ans + 1);
return ans;
}
}
…
1546. 和为目标值的最大数目不重叠非空子数组数目
English Version
题目描述
给你一个数组 nums 和一个整数 target 。
请你返回 非空不重叠 子数组的最大数目,且每个子数组中数字和都为 target 。
示例 1:
输入:nums = [1,1,1,1,1], target = 2 输出:2 解释:总共有 2 个不重叠子数组(加粗数字表示) [1,1,1,1,1] ,它们的和为目标值 2 。
示例 2:
输入:nums = [-1,3,5,1,4,2,-9], target = 6 输出:2 解释:总共有 3 个子数组和为 6 。 ([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。
示例 3:
输入:nums = [-2,6,6,3,5,4,1,2,8], target = 10 输出:3
示例 4:
输入:nums = [0,0,0], target = 0 输出:3
提示:
1 <= nums.length <= 10^5-10^4 <= nums[i] <= 10^40 <= target <= 10^6
解法
Python3
Java
class Solution {
public int maxNonOverlapping(int[] nums, int target) {
Set<Integer> set = new HashSet<>();
set.add(0);
int sum = 0, ans = 0;
for (int num : nums) {
sum += num;
if (set.contains(sum - target)) {
ans++;
set.clear();
sum = 0;
}
set.add(sum);
}
return ans;
}
}
…
1550. 存在连续三个奇数的数组
English Version
题目描述
给你一个整数数组 arr,请你判断数组中是否存在连续三个元素都是奇数的情况:如果存在,请返回 true ;否则,返回 false 。
示例 1:
输入:arr = [2,6,4,1] 输出:false 解释:不存在连续三个元素都是奇数的情况。
示例 2:
输入:arr = [1,2,34,3,4,5,7,23,12] 输出:true 解释:存在连续三个元素都是奇数的情况,即 [5,7,23] 。
提示:
1 <= arr.length <= 10001 <= arr[i] <= 1000
解法
Python3
Java
class Solution {
public boolean threeConsecutiveOdds(int[] arr) {
int count = 0;
for (int n : arr) {
if (n % 2 == 0) {
count = 0;
} else {
count++;
if (count >= 3) {
return true;
}
}
}
return false;
}
}
…
1551. 使数组中所有元素相等的最小操作数
English Version
题目描述
存在一个长度为 n 的数组 arr ,其中 arr[i] = (2 * i) + 1 ( 0 <= i < n )。
一次操作中,你可以选出两个下标,记作 x 和 y ( 0 <= x, y < n )并使 arr[x] 减去 1 、arr[y] 加上 1 (即 arr[x] -=1 且 arr[y] += 1 )。最终的目标是使数组中的所有元素都 相等 。题目测试用例将会 保证 :在执行若干步操作后,数组中的所有元素最终可以全部相等。
给你一个整数 n,即数组的长度。请你返回使数组 arr 中所有元素相等所需的 最小操作数 。
示例 1:
输入:n = 3 输出:2 解释:arr = [1, 3, 5] 第一次操作选出 x = 2 和 y = 0,使数组变为 [2, 3, 4] 第二次操作继续选出 x = 2 和 y = 0,数组将会变成 [3, 3, 3]
示例 2:
输入:n = 6 输出:9
提示:
1 <= n <= 10^4
解法
Python3
Java
class Solution {
public int minOperations(int n) {
int ans = 0;
for (int i = 0; i < n / 2; i++) {
int curr = 2 * i + 1;
ans += Math.abs(n - curr);
}
return ans;
}
}
…
1552. 两球之间的磁力
English Version
题目描述
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
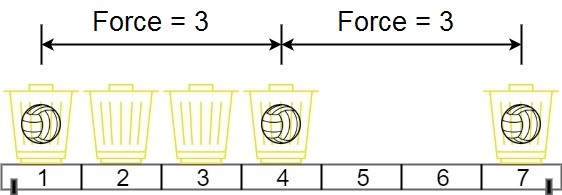输入:position = [1,2,3,4,7], m = 3 输出:3 解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2 输出:999999999 解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
解法
Python3
Java
class Solution {
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
// 最小磁力的可能最小值
int min = 1;
// 最小磁力的可能最大值
int max = (position[position.length - 1] - position[0]) / (m - 1);
int ans = -1;
while (min <= max) {
int mid = (min + max) / 2;
if (checkDistance(mid, position, m)) {
ans = mid;
min = mid + 1;
} else {
max = mid - 1;
}
}
return ans;
}
private boolean checkDistance(int mid, int[] position, int m) {
int count = 1;
int pre = position[0];
for (int i = 1; i < position.length; i++) {
if (position[i] - pre >= mid) {
count++;
if (count >= m) {
return true;
}
pre = position[i];
}
}
return false;
}
}
…
1553. 吃掉 N 个橘子的最少天数
English Version
题目描述
厨房里总共有 n 个橘子,你决定每一天选择如下方式之一吃这些橘子:
- 吃掉一个橘子。
- 如果剩余橘子数
n能被 2 整除,那么你可以吃掉n/2个橘子。 - 如果剩余橘子数
n能被 3 整除,那么你可以吃掉2*(n/3)个橘子。
每天你只能从以上 3 种方案中选择一种方案。
请你返回吃掉所有 n 个橘子的最少天数。
示例 1:
输入:n = 10 输出:4 解释:你总共有 10 个橘子。 第 1 天:吃 1 个橘子,剩余橘子数 10 - 1 = 9。 第 2 天:吃 6 个橘子,剩余橘子数 9 - 2*(9/3) = 9 - 6 = 3。(9 可以被 3 整除) 第 3 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。 第 4 天:吃掉最后 1 个橘子,剩余橘子数 1 - 1 = 0。 你需要至少 4 天吃掉 10 个橘子。
示例 2:
输入:n = 6 输出:3 解释:你总共有 6 个橘子。 第 1 天:吃 3 个橘子,剩余橘子数 6 - 6/2 = 6 - 3 = 3。(6 可以被 2 整除) 第 2 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。(3 可以被 3 整除) 第 3 天:吃掉剩余 1 个橘子,剩余橘子数 1 - 1 = 0。 你至少需要 3 天吃掉 6 个橘子。
示例 3:
输入:n = 1 输出:1
示例 4:
输入:n = 56 输出:6
提示:
1 <= n <= 2*10^9
解法
Python3
Java
class Solution {
private Map<Integer, Integer> map = new HashMap<>();
public int minDays(int n) {
if (n < 2) {
return n;
}
if (!map.containsKey(n)) {
map.put(n, Math.min(minDays(n / 2) + 1 + n % 2, minDays(n / 3) + 1 + n % 3));
}
return map.get(n);
}
}
…
1560. 圆形赛道上经过次数最多的扇区
English Version
题目描述
给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成,扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛,该马拉松全程由 m 个阶段组成。其中,第 i 个阶段将会从扇区 rounds[i - 1] 开始,到扇区 rounds[i] 结束。举例来说,第 1 阶段从 rounds[0] 开始,到 rounds[1] 结束。
请你以数组形式返回经过次数最多的那几个扇区,按扇区编号 升序 排列。
注意,赛道按扇区编号升序逆时针形成一个圆(请参见第一个示例)。
示例 1:
输入:n = 4, rounds = [1,3,1,2] 输出:[1,2] 解释:本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示: 1 --> 2 --> 3(阶段 1 结束)--> 4 --> 1(阶段 2 结束)--> 2(阶段 3 结束,即本场马拉松结束) 其中,扇区 1 和 2 都经过了两次,它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。
示例 2:
输入:n = 2, rounds = [2,1,2,1,2,1,2,1,2] 输出:[2]
示例 3:
输入:n = 7, rounds = [1,3,5,7] 输出:[1,2,3,4,5,6,7]
提示:
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1],其中0 <= i < m
解法
Python3
Java
class Solution {
public List<Integer> mostVisited(int n, int[] rounds) {
int[] ans = new int[n];
for (int i = 0; i < rounds.length; i++) {
rounds[i]--;
}
ans[rounds[0]]++;
for (int i = 0; i < rounds.length - 1; i++) {
int start = rounds[i];
int end = rounds[i + 1];
if (end <= start) {
end += n;
}
for (int j = start + 1; j <= end; j++) {
ans[j % n]++;
}
}
int max = Arrays.stream(ans).max().orElse(-1);
List<Integer> list = new ArrayList<>();
for (int i = 0; i < ans.length; i++) {
if (ans[i] == max) {
list.add(i + 1);
}
}
return list;
}
}
…
1561. 你可以获得的最大硬币数目
[English Version](/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README_EN.md)
题目描述
有 3n 堆数目不一的硬币,你和你的朋友们打算按以下方式分硬币:
- 每一轮中,你将会选出 任意 3 堆硬币(不一定连续)。
- Alice 将会取走硬币数量最多的那一堆。
- 你将会取走硬币数量第二多的那一堆。
- Bob 将会取走最后一堆。
- 重复这个过程,直到没有更多硬币。
给你一个整数数组 piles ,其中 piles[i] 是第 i 堆中硬币的数目。
返回你可以获得的最大硬币数目。
示例 1:
输入:piles = [2,4,1,2,7,8] 输出:9 解释:选出 (2, 7, 8) ,Alice 取走 8 枚硬币的那堆,你取走 7 枚硬币的那堆,Bob 取走最后一堆。 选出 (1, 2, 4) , Alice 取走 4 枚硬币的那堆,你取走 2 枚硬币的那堆,Bob 取走最后一堆。 你可以获得的最大硬币数目:7 + 2 = 9. 考虑另外一种情况,如果选出的是 (1, 2, 8) 和 (2, 4, 7) ,你就只能得到 2 + 4 = 6 枚硬币,这不是最优解。
示例 2:
输入:piles = [2,4,5] 输出:4
示例 3:
输入:piles = [9,8,7,6,5,1,2,3,4] 输出:18
提示:
3 <= piles.length <= 10^5piles.length % 3 == 01 <= piles[i] <= 10^4
解法
Python3
Java
class Solution {
public int maxCoins(int[] piles) {
Arrays.sort(piles);
int start = 0, end = piles.length - 1, ans = 0;
while (start < end) {
ans += piles[end - 1];
start++;
end -= 2;
}
return ans;
}
}
…
1562. 查找大小为 M 的最新分组
English Version
题目描述
给你一个数组 arr ,该数组表示一个从 1 到 n 的数字排列。有一个长度为 n 的二进制字符串,该字符串上的所有位最初都设置为 0 。
在从 1 到 n 的每个步骤 i 中(假设二进制字符串和 arr 都是从 1 开始索引的情况下),二进制字符串上位于位置 arr[i] 的位将会设为 1 。
给你一个整数 m ,请你找出二进制字符串上存在长度为 m 的一组 1 的最后步骤。一组 1 是一个连续的、由 1 组成的子串,且左右两边不再有可以延伸的 1 。
返回存在长度 恰好 为 m 的 一组 1 的最后步骤。如果不存在这样的步骤,请返回 -1 。
示例 1:
输入:arr = [3,5,1,2,4], m = 1 输出:4 解释: 步骤 1:"00100",由 1 构成的组:["1"] 步骤 2:"00101",由 1 构成的组:["1", "1"] 步骤 3:"10101",由 1 构成的组:["1", "1", "1"] 步骤 4:"11101",由 1 构成的组:["111", "1"] 步骤 5:"11111",由 1 构成的组:["11111"] 存在长度为 1 的一组 1 的最后步骤是步骤 4 。
示例 2:
输入:arr = [3,1,5,4,2], m = 2 输出:-1 解释: 步骤 1:"00100",由 1 构成的组:["1"] 步骤 2:"10100",由 1 构成的组:["1", "1"] 步骤 3:"10101",由 1 构成的组:["1", "1", "1"] 步骤 4:"10111",由 1 构成的组:["1", "111"] 步骤 5:"11111",由 1 构成的组:["11111"] 不管是哪一步骤都无法形成长度为 2 的一组 1 。
示例 3:
输入:arr = [1], m = 1 输出:1
示例 4:
输入:arr = [2,1], m = 2 输出:2
提示:
n == arr.length1 <= n <= 10^51 <= arr[i] <= narr中的所有整数 互不相同1 <= m <= arr.length
解法
Python3
Java
class Solution {
public int findLatestStep(int[] arr, int m) {
// 倒序遍历 arr,转换为第一次出现 m 个的步骤
if (arr.length == m) {
return m;
}
TreeSet<Integer> set = new TreeSet<>();
set.add(0);
set.add(arr.length + 1);
for (int i = arr.length - 1; i >= 0; i--) {
int index = arr[i];
int l = set.lower(index);
int h = set.higher(index);
if (index - l - 1 == m || h - index - 1 == m) {
return i;
}
set.add(index);
}
return -1;
}
}
…
1566. 重复至少 K 次且长度为 M 的模式
English Version
题目描述
给你一个正整数数组 arr,请你找出一个长度为 m 且在数组中至少重复 k 次的模式。
模式 是由一个或多个值组成的子数组(连续的子序列),连续 重复多次但 不重叠 。 模式由其长度和重复次数定义。
如果数组中存在至少重复 k 次且长度为 m 的模式,则返回 true ,否则返回 false 。
示例 1:
输入:arr = [1,2,4,4,4,4], m = 1, k = 3 输出:true 解释:模式 (4) 的长度为 1 ,且连续重复 4 次。注意,模式可以重复 k 次或更多次,但不能少于 k 次。
示例 2:
输入:arr = [1,2,1,2,1,1,1,3], m = 2, k = 2 输出:true 解释:模式 (1,2) 长度为 2 ,且连续重复 2 次。另一个符合题意的模式是 (2,1) ,同样重复 2 次。
示例 3:
输入:arr = [1,2,1,2,1,3], m = 2, k = 3 输出:false 解释:模式 (1,2) 长度为 2 ,但是只连续重复 2 次。不存在长度为 2 且至少重复 3 次的模式。
示例 4:
输入:arr = [1,2,3,1,2], m = 2, k = 2 输出:false 解释:模式 (1,2) 出现 2 次但并不连续,所以不能算作连续重复 2 次。
示例 5:
输入:arr = [2,2,2,2], m = 2, k = 3 输出:false 解释:长度为 2 的模式只有 (2,2) ,但是只连续重复 2 次。注意,不能计算重叠的重复次数。
提示:
2 <= arr.length <= 1001 <= arr[i] <= 1001 <= m <= 1002 <= k <= 100
解法
Python3
Java
class Solution {
public boolean containsPattern(int[] arr, int m, int k) {
if (arr.length < m * k) {
return false;
}
for (int i = 0; i <= arr.length - m * k; i++) {
boolean match = true;
for (int j = i + m; j < i + m * k; j++) {
if (arr[j] != arr[j - m]) {
match = false;
break;
}
}
if (match) {
return true;
}
}
return false;
}
}
…
1567. 乘积为正数的最长子数组长度
English Version
题目描述
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。
一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
示例 1:
输入:nums = [1,-2,-3,4] 输出:4 解释:数组本身乘积就是正数,值为 24 。
示例 2:
输入:nums = [0,1,-2,-3,-4] 输出:3 解释:最长乘积为正数的子数组为 [1,-2,-3] ,乘积为 6 。 注意,我们不能把 0 也包括到子数组中,因为这样乘积为 0 ,不是正数。
示例 3:
输入:nums = [-1,-2,-3,0,1] 输出:2 解释:乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。
示例 4:
输入:nums = [-1,2] 输出:1
示例 5:
输入:nums = [1,2,3,5,-6,4,0,10] 输出:4
提示:
1 <= nums.length <= 10^5-10^9 <= nums[i] <= 10^9
解法
Python3
Java
class Solution {
public int getMaxLen(int[] nums) {
// p[i] = n[i-1] + 1, nums[i] < 0
// p[i] = p[i-1] + 1, nums[i] > 0
// p[i] = 0, nums[i] = 0
// n[i] = p[i-1] + 1, nums[i] < 0
// n[i] = n[i-1] + 1, nums[i] > 0
// n[i] = 0, nums[i] = 0
int[] p = new int[nums.length];
int[] n = new int[nums.length];
p[0] = nums[0] > 0 ? 1 : 0;
n[0] = nums[0] < 0 ? 1 : 0;
int res = Math.max(p[0], 0);
for (int i = 1; i < nums.length; i++) {
if (nums[i] > 0) {
p[i] = p[i - 1] + 1;
n[i] = n[i - 1] == 0 ? 0 : n[i - 1] + 1;
} else if (nums[i] == 0) {
p[i] = 0;
n[i] = 0;
} else {
p[i] = n[i - 1] == 0 ? 0 : n[i - 1] + 1;
n[i] = p[i - 1] + 1;
}
res = Math.max(res, p[i]);
}
return res;
}
}
…
1569. 将子数组重新排序得到同一个二叉查找树的方案数
English Version
题目描述
给你一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums 中的顺序依次插入一个初始为空的二叉查找树(BST)。请你统计将 nums 重新排序后,统计满足如下条件的方案数:重排后得到的二叉查找树与 nums 原本数字顺序得到的二叉查找树相同。
比方说,给你 nums = [2,1,3],我们得到一棵 2 为根,1 为左孩子,3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST,但 [3,2,1] 会得到一棵不同的 BST 。
请你返回重排 nums 后,与原数组 nums 得到相同二叉查找树的方案数。
由于答案可能会很大,请将结果对 10^9 + 7 取余数。
示例 1:
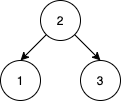输入:nums = [2,1,3] 输出:1 解释:我们将 nums 重排, [2,3,1] 能得到相同的 BST 。没有其他得到相同 BST 的方案了。
示例 2:
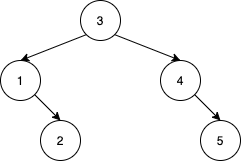输入:nums = [3,4,5,1,2] 输出:5 解释:下面 5 个数组会得到相同的 BST: [3,1,2,4,5] [3,1,4,2,5] [3,1,4,5,2] [3,4,1,2,5] [3,4,1,5,2]
示例 3:
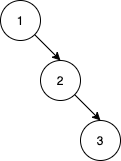输入:nums = [1,2,3] 输出:0 解释:没有别的排列顺序能得到相同的 BST 。
示例 4:
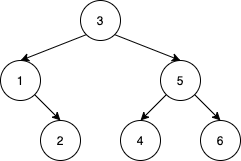输入:nums = [3,1,2,5,4,6] 输出:19
示例 5:
输入:nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18] 输出:216212978 解释:得到相同 BST 的方案数是 3216212999。将它对 10^9 + 7 取余后得到 216212978。
提示:
1 <= nums.length <= 10001 <= nums[i] <= nums.lengthnums中所有数 互不相同 。
解法
Python3
Java
class Solution {
int mod = (int) 1e9 + 7;
public int numOfWays(int[] nums) {
if (nums.length < 2) {
return 0;
}
return dfs(Arrays.stream(nums).boxed().collect(Collectors.toList()), calc(nums.length)) - 1;
}
private int dfs(List<Integer> list, int[][] c) {
if (list.isEmpty()) {
return 1;
}
List<Integer> left = list.stream().filter(n -> n < list.get(0))
.collect(Collectors.toList());
List<Integer> right = list.stream().filter(n -> n > list.get(0))
.collect(Collectors.toList());
return (int) ((long) c[list.size() - 1][left.size()] * dfs(left, c) % mod * dfs(right, c)
% mod);
}
private int[][] calc(int n) {
int[][] c = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0) {
c[i][j] = 1;
} else {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
}
return c;
}
}
…
1572. 矩阵对角线元素的和
English Version
题目描述
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
输入:mat = [[1,2,3], [4,5,6], [7,8,9]] 输出:25 解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25 请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1], [1,1,1,1], [1,1,1,1], [1,1,1,1]] 输出:8
示例 3:
输入:mat = [[5]] 输出:5
提示:
n == mat.length == mat[i].length1 <= n <= 1001 <= mat[i][j] <= 100
解法
Python3
Java
class Solution {
public int diagonalSum(int[][] mat) {
int sum = 0, n = mat.length, mid = n >> 1;
for (int i = 0, j = n - 1; i < n; i++, j--) {
sum += (mat[i][i] + mat[i][j]);
}
return n % 2 == 0 ? sum : sum - mat[mid][mid];
}
}
…
1573. 分割字符串的方案数
English Version
题目描述
给你一个二进制串 s (一个只包含 0 和 1 的字符串),我们可以将 s 分割成 3 个 非空 字符串 s1, s2, s3 (s1 + s2 + s3 = s)。
请你返回分割 s 的方案数,满足 s1,s2 和 s3 中字符 '1' 的数目相同。
由于答案可能很大,请将它对 10^9 + 7 取余后返回。
示例 1:
输入:s = "10101" 输出:4 解释:总共有 4 种方法将 s 分割成含有 '1' 数目相同的三个子字符串。 "1|010|1" "1|01|01" "10|10|1" "10|1|01"
示例 2:
输入:s = "1001" 输出:0
示例 3:
输入:s = "0000" 输出:3 解释:总共有 3 种分割 s 的方法。 "0|0|00" "0|00|0" "00|0|0"
示例 4:
输入:s = "100100010100110" 输出:12
提示:
s[i] == '0'或者s[i] == '1'3 <= s.length <= 10^5
解法
Python3
Java
class Solution {
public int numWays(String s) {
char[] chars = s.toCharArray();
List<Long> p = new ArrayList<>();
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '1') {
p.add((long) i);
}
}
int l = p.size();
if (l % 3 != 0) {
return 0;
}
int MOD = (int) (1e9 + 7);
if (l == 0) {
return (int) (((long) (s.length() - 1) * (s.length() - 2) / 2) % MOD);
}
// 每 n/3 的地方为分界线
return (int) ((p.get(l / 3) - p.get(l / 3 - 1)) * (p.get(2 * l / 3) - p.get(2 * l / 3 - 1))
% MOD);
}
}
…
1574. 删除最短的子数组使剩余数组有序
English Version
题目描述
给你一个整数数组 arr ,请你删除一个子数组(可以为空),使得 arr 中剩下的元素是 非递减 的。
一个子数组指的是原数组中连续的一个子序列。
请你返回满足题目要求的最短子数组的长度。
示例 1:
输入:arr = [1,2,3,10,4,2,3,5] 输出:3 解释:我们需要删除的最短子数组是 [10,4,2] ,长度为 3 。剩余元素形成非递减数组 [1,2,3,3,5] 。 另一个正确的解为删除子数组 [3,10,4] 。
示例 2:
输入:arr = [5,4,3,2,1] 输出:4 解释:由于数组是严格递减的,我们只能保留一个元素。所以我们需要删除长度为 4 的子数组,要么删除 [5,4,3,2],要么删除 [4,3,2,1]。
示例 3:
输入:arr = [1,2,3] 输出:0 解释:数组已经是非递减的了,我们不需要删除任何元素。
示例 4:
输入:arr = [1] 输出:0
提示:
1 <= arr.length <= 10^50 <= arr[i] <= 10^9
解法
Python3
Java
class Solution {
public int findLengthOfShortestSubarray(int[] arr) {
int n = arr.length;
int left = 0;
while (left + 1 < n && arr[left] <= arr[left + 1]) {
left++;
}
if (left == n - 1) {
return 0;
}
int right = n - 1;
while (right > 0 && arr[right - 1] <= arr[right]) {
right--;
}
int res = Math.min(n - left - 1, right);
int i = 0, j = right;
while (i <= left && j <= n - 1) {
if (arr[i] <= arr[j]) {
res = Math.min(res, j - i - 1);