Matplotlib详解

1.简单的折线图

对于图表来说，最简单的莫过于作出一个单一函数的图像。

# 导入相关的包
import numpy as np
# 关闭警告
import warnings
warnings.filterwarnings('ignore')   
      
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
      
plt.rcParams["font.sans-serif"] = ["SimHei"] 
plt.rcParams["axes.unicode_minus"] = False
plt.rcParams['figure.figsize'] = (10, 6)  # 设置figure_size尺寸
plt.rcParams['figure.dpi'] = 100         # 图像分辨率

对于所有的 Matplotlib 图表来说，我们都需要从创建图形和维度开始。图形和维度可以使用下面代码进行最简形式的创建：

# 创建空白图表
fig = plt.figure()
ax = plt.axes()

在 Matplotlib 中，图形（类plt.Figure的一个实例）可以被认为是一个包括所有维度、图像、文本和标签对象的容器。维度（类plt.Axes的一个实例）就是你上面看到的图像，一个有边界的格子包括刻度和标签，最终还有我们画在上面的图表元素。后面，我们会使用变量名fig来指代图形对象，以及变量名ax来指代维度变量。
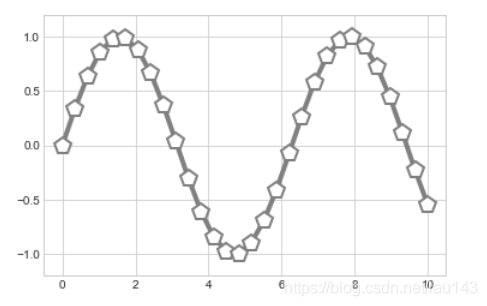
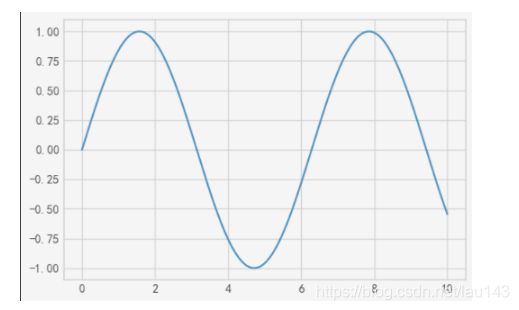
一旦我们创建了维度，我们可以使用ax.plot方法将数据绘制在图表上。下面是一个简单的正弦函数图形：

fig = plt.figure()   # 图形对象
ax = plt.axes()     # 维度变量
         
x = np.linspace(0, 10, 1000)
ax.plot(x, np.sin(x));

同样的，我们可以使用 pylab 接口（MATLAB 风格的接口）帮我们在后台自动创建这两个对象：

plt.plot(x, np.sin(x))

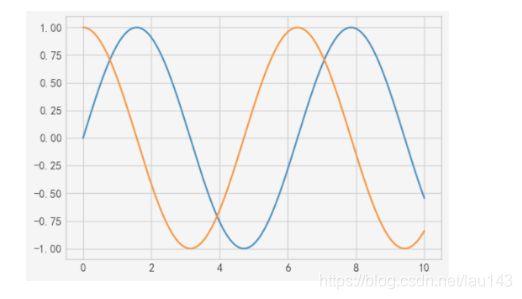
如果我们需要在同一幅图形中绘制多根线条，只需要多次调用plot函数即可：

   plt.plot(x, np.sin(x))
   plt.plot(x, np.cos(x))

这就是在 Matplotlib 中绘制简单函数图像的所有接口了。下面我们深入了解一下控制坐标轴和线条外观的细节。

1.1 线条颜色和风格

• 表示颜色的字符参数有
  ‘b’：蓝色
  ‘g’：绿色
  ‘r’：红色
  ‘c’：青色，cyan
  ‘m’：品红，magenta
  ‘y’：黄色
  ‘k’：黑色
• 所有 HTML 颜色名称可以在这里找到。

  plt.plot(x, np.sin(x - 0), color='blue')        # 通过颜色名称指定
  plt.plot(x, np.sin(x - 1), color='g')           # 通过颜色简写名称指定(rgbcmyk)
  plt.plot(x, np.sin(x - 2), color='0.75')        # 介于0-1之间的灰阶值
  plt.plot(x, np.sin(x - 3), color='#FFDD44')     # 16进制的RRGGBB值
  plt.plot(x, np.sin(x - 4), color=(1.0,0.2,0.3)) # RGB元组的颜色值，每个值介于0-1
  plt.plot(x, np.sin(x - 5), color='chartreuse'); # 能支持所有HTML颜色名称值

• 通过linestyle关键字参数可以指定线条的风格：
  表示类型的字符参数有：
  

  plt.plot(x, x + 0, linestyle='solid')
  plt.plot(x, x + 1, linestyle='dashed')
  plt.plot(x, x + 2, linestyle='dashdot')
  plt.plot(x, x + 3, linestyle='dotted');
      
 # 还可以用形象的符号代表线条风格
  plt.plot(x, x + 4, linestyle='-')  # 实线
  plt.plot(x, x + 5, linestyle='--') # 虚线
  plt.plot(x, x + 6, linestyle='-.') # 长短点虚线
  plt.plot(x, x + 7, linestyle=':');  # 点线

• 这些linestyle和color参数能够合并成一个非关键字参数，传递给plt.plot()函数：

 plt.plot(x, x + 0, '-g')  # 绿色实线
 plt.plot(x, x + 1, '--c') # 天青色虚线
 plt.plot(x, x + 2, '-.k') # 黑色长短点虚线
 plt.plot(x, x + 3, ':r');  # 红色点线

1.2 坐标轴范围

Matplotlib 会自动选择非常合适的坐标轴范围来绘制图像，但是有些情况下也需要自己进行相关调整。
使用plt.xlim()和plt.ylim()函数可以调整坐标轴的范围：

• 如果某些情况下你希望将坐标轴反向，你可以通过上面的函数实现，将参数顺序颠倒即可：

plt.plot(x, np.sin(x))
plt.xlim(10, 0)
plt.ylim(1.2, -1.2)

• 相关的函数还有plt.axis()这个函数可以在一个函数调用中就完成 x 轴和 y 轴范围的设置，
  传递一个[xmin, xmax, ymin, ymax]的列表参数即可：

 plt.plot(x, np.sin(x))
 plt.axis([-1, 11, -1.5, 1.5]);

• plt.axis()函数不仅能设置范围，还能像下面代码一样将坐标轴压缩到刚好足够绘制折线图像的大小：

plt.plot(x, np.sin(x))
plt.axis('tight')

• 还可以通过设置’equal’参数设置x轴与y轴使用相同的长度单位

   plt.plot(x, np.sin(x))
   plt.axis('equal')

更多关于设置 axis 属性的内容请查阅plt.axis函数的文档字符串。

1.3 折线图标签

• 标题和坐标轴标签

      plt.plot(x, np.sin(x))
      plt.title("A Sine Curve")
      plt.xlabel("x")
      plt.ylabel("sin(x)")

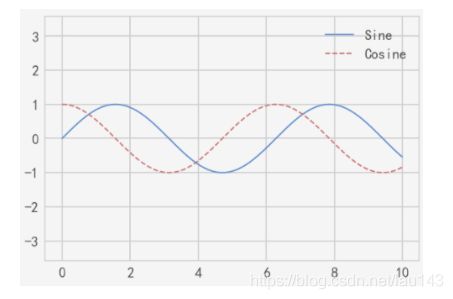
• 创建图例
  通过plt.legend()函数可以实现这个需求。虽然有很多种正确的方法来指定图例，最简单的方法是通过在绘制每条线条时指定对应的label关键字参数来使用这个函数：

plt.plot(x, np.sin(x), '-g', label='sin(x)')
plt.plot(x, np.cos(x), ':b', label='cos(x)')
plt.axis('equal')
        
plt.legend()			

上图可见，plt.legend()函数绘制的图例线条与图中的折线无论风格和颜色都保持一致。

1.4额外内容：Matplotlib 的坑

虽然大多数的plt函数都可以直接转换为ax的方法进行调用（例如plt.plot() → ax.plot()，plt.legend() → ax.legend()等），但是并不是所有的命令都能应用这种情况。特别是用于设置极值、标签和标题的函数都有一定的改变。下表列出了将 MATLAB 风格的函数转换为面向对象的方法的区别：

• plt.xlabel() → ax.set_xlabel()
• plt.ylabel() → ax.set_ylabel()
• plt.xlim() → ax.set_xlim()
• plt.ylim() → ax.set_ylim()
• plt.title() → ax.set_title()

在面向对象接口中，与其逐个调用上面的方法来设置属性，更常见的使用ax.set()方法来一次性设置所有的属性：

    ax = plt.axes()
    ax.plot(x, np.sin(x))
    ax.set(xlim=(0, 10), ylim=(-2, 2),
    		xlabel='x', ylabel='sin(x)',
    		title='A Simple Plot')

2.简单散点图

另一种常用的图表类型是简单散点图，它是折线图的近亲。不像折线图，图中的点连接起来组成连线，散点图中的点都是独立分布的点状、圆圈或其他形状

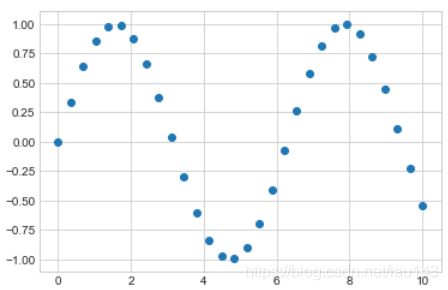
2.1 使用 plt.plot 绘制散点图

绘制散点图：

 x = np.linspace(0, 10, 30)
 y = np.sin(x)
   
 plt.plot(x, y, 'o', color='black')

传递给函数的第三个参数是使用一个字符代表的图表绘制点的类型。就像你可以使用’-‘或’–'来控制线条的风格那样，点的类型风格也可以使用短字符串代码来表示。下面的例子可以展示那些最通用的符号：

  rng = np.random.RandomState(0)
  for marker in ['o', '.', ',', 'x', '+', 'v', '^', '<', '>', 's', 'd']:
        plt.plot(rng.rand(5), rng.rand(5), marker,
                 label="marker='{0}'".format(marker))
    plt.legend(numpoints=1)
    plt.xlim(0, 1.8)

plt.plot还有很多额外的关键字参数用来指定广泛的线条和点的属性：

    plt.plot(x, y, '-p', color='gray',
             markersize=15, linewidth=4,
             markerfacecolor='white',
             markeredgecolor='gray',
             markeredgewidth=2)
    plt.ylim(-1.2, 1.2)

2.2 使用plt.scatter绘制散点图

第二种更强大的绘制散点图的方法是使用plt.scatter函数，它的使用方法和plt.plot类似

  plt.scatter(x, y, marker='o')

• plt.scatter和plt.plot的主要区别在于，plt.scatter可以针对每个点设置不同属性（大小、填充颜色、边缘颜色等），还可以通过数据集合对这些属性进行设置。
• 下面通过一个随机值数据集绘制不同颜色和大小的散点图来说明。为了更好的查看重叠的结果，我们还使用了alpha关键字参数对点的透明度进行了调整：

  rng = np.random.RandomState(0)
  x = rng.randn(100)
  y = rng.randn(100)
  colors = rng.rand(100)
  sizes = 1000 * rng.rand(100)
      
  plt.scatter(x, y, c=colors, s=sizes, alpha=0.3,cmap='viridis')
  plt.colorbar()   # 显示颜色对比条

注意图表右边有一个颜色对比条（这里通过colormap()函数输出），图表中的点大小的单位是像素。使用这种方法，散点的颜色和大小都能用来展示数据信息，在希望展示多个维度数据集合的情况下很直观。

• 例如，当我们使用 Scikit-learn 中的鸢尾花数据集，里面的每个样本都是三种鸢尾花中的其中一种，并带有仔细测量的花瓣和花萼的尺寸数据：

  from sklearn.datasets import load_iris
  iris = load_iris()
  features = iris.data.T
        
  plt.scatter(features[0], features[1], alpha=0.2, s=100*features[3], c=iris.target, cmap='viridis')
  plt.xlabel(iris.feature_names[0])
  plt.ylabel(iris.feature_names[1])

我们可以从上图中看出，可以通过散点图同时展示该数据集的四个不同维度：
图中的(x, y)位置代表每个样本的花萼的长度和宽度，散点的大小代表每个样本的花瓣的宽度，
而散点的颜色代表一种特定的鸢尾花类型。
plot 和 scatter 对比：性能提醒
除了上面说的plt.plot和plt.scatter对于每个散点不同属性的支持不同之外，还有别的因素影响对这两个函数的选择吗？对于小的数据集来说，两者并无差别，当数据集增长到几千个点时，plt.plot会明显比plt.scatter的性能要高。造成这个差异的原因是plt.scatter支持每个点使用不同的大小和颜色，因此渲染每个点时需要完成更多额外的工作。而plt.plot来说，每个点都是简单的复制另一个点产生，因此对于整个数据集来说，确定每个点的展示属性的工作仅需要进行一次即可。对于很大的数据集来说，这个差异会导致两者性能的巨大区别，因此，对于大数据集应该优先使用plt.plot函数。

3.直方图

一个简单的直方图可以是我们开始理解数据集的第一步。前面我们看到了 Matplotlib 的直方图函数，我们可以用一行代码绘制基础的直方图

 data = np.random.randn(1000)
 plt.hist(data)

hist()函数有很多的参数可以用来调整运算和展示；下面又一个更加个性化的直方图展示：

    plt.hist(data, bins=30, density=True, alpha=0.5,
             histtype='stepfilled', color='steelblue',
             edgecolor='none')

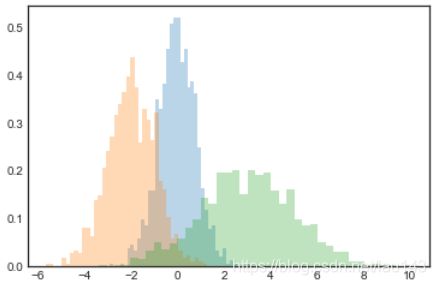
使用histtype='stepfilled’和alpha参数设置透明度在对不同分布的数据集进行比较展示时很有用：

  x1 = np.random.normal(0, 0.8, 1000)
  x2 = np.random.normal(-2, 1, 1000)
  x3 = np.random.normal(3, 2, 1000)
    
  kwargs = dict(histtype='stepfilled', alpha=0.3, density=True, bins=40)
    
  plt.hist(x1, **kwargs)
  plt.hist(x2, **kwargs)
  plt.hist(x3, **kwargs)

如果你只是需要计算直方图的数值（即每个桶的数据点数量）而不是展示图像，np.histogram()函数可以完成这个目标：

counts, bin_edges = np.histogram(data, bins=5)
print(counts)
# 输出结果
[ 33 273 509 173  12]

4.自定义图标图例

图例可以为可视化赋予实际含义，为不同的图标元素附上明确说明。我们前面看到了一些简单的图例创建例子；
下面我们来介绍一下在 Matplotlib 中自定义图例的位置和进行美化的方法

可以使用plt.legend()函数来创建最简单的图例，这个函数能自动创建任何带有标签属性的图表元素的图例：

  x = np.linspace(0, 10, 1000)
  fig, ax = plt.subplots()
  ax.plot(x, np.sin(x), '-b', label='Sine')
  ax.plot(x, np.cos(x), '--r', label='Cosine')
  ax.axis('equal')
  leg = ax.legend()

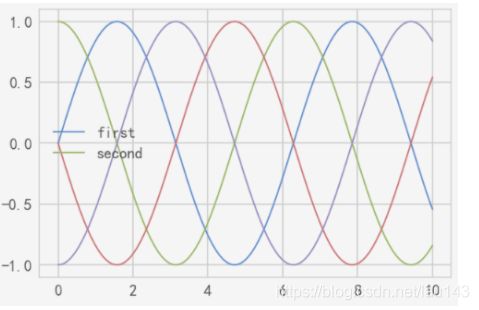
 y = np.sin(x[:, np.newaxis] + np.pi * np.arange(0, 2, 0.5))
 lines = plt.plot(x, y)
    
 # lines是一个线条实例的列表
 plt.legend(lines[:2], ['first', 'second'])

5.在 matplotlib 中创建三维图表

Matplotlib 最开始被设计为仅支持二维的图表。到 1.0 版本发布左右，一些三维图表的工具在二维展示的基础上被创建了出来，结果就是 Matplotlib 提供了一个方便的（同时也是有限的）的可用于三维数据可视化的一套工具。三维图表可以使用载入mplot3d工具包来激活，这个包会随着 Matplotlib 自动安装：

from mpl_toolkits import mplot3d
    
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
    
fig = plt.figure()
ax = plt.axes(projection='3d')

三维 axes 激活后，我们可以在上面绘制不同的三维图表类型。三维图表在 notebook 中使用交互式图表展示会优于使用静态展示；
你可以使用%matplotlib notebook而不是%matplotlib inline来激活交互式展示模式。

5.1 三维的点和线

三维图表中最基础的是使用(x, y, z)坐标定义的一根线或散点的集合。前面介绍过普通的二维图表，作为类比，使用ax.plot3D和ax.scatter3D函数可以创建三维折线和散点图。这两个函数的签名与二维的版本基本一致，下面我们绘制一个三维中的三角螺旋，在线的附近在绘制一些随机的点：

    ax = plt.axes(projection='3d')
    
    # 三维螺旋线的数据
    zline = np.linspace(0, 15, 1000)
    xline = np.sin(zline)
    yline = np.cos(zline)
    ax.plot3D(xline, yline, zline, 'gray')
    
    # 三维散点的数据
    zdata = 15 * np.random.random(100)
    xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
    ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
    ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens')

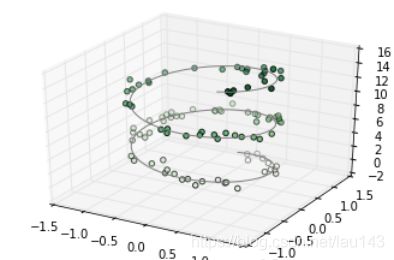
注意默认情况下，图中的散点会有透明度的区别，用于体现在图中散点的深度。虽然三维效果在静态图像中难以显示，你可以使用交互式的视图来获得更佳的三维直观效果。

5.2 三维轮廓图

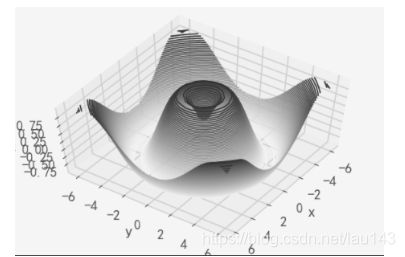
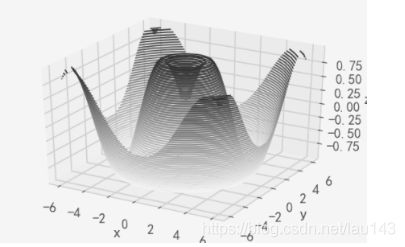
类似于我们在[密度和轮廓图]中介绍的内容，mplot3d也包含着能够创建三维浮雕图像的工具。就像二维的ax.contour图表，ax.contour3D要求输入数据的格式是二维普通网格上计算得到的 Z 轴的数据值。下面我们展示一个三维的正弦函数轮廓图：

 def f(x, y):
        return np.sin(np.sqrt(x ** 2 + y ** 2))
    
    x = np.linspace(-6, 6, 30)
    y = np.linspace(-6, 6, 30)
    
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    
    fig = plt.figure()
    ax = plt.axes(projection='3d')
    ax.contour3D(X, Y, Z, 50, cmap='binary')
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')

有时候默认的视角角度不是最理想的，在这种情况下我们可以使用view_init函数来设置水平角和方位角。在下面的例子中，我们使用的是 60° 的水平角（即以 60° 俯视 x-y 平面）和 35° 的方位角（即将 z 轴逆时针旋转 35°）：

  ax.view_init(60, 35)
  fig

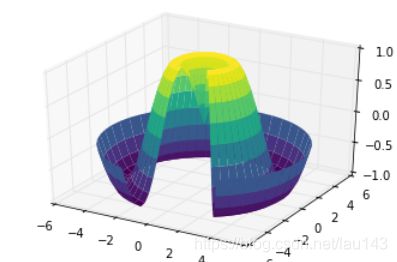
5.3 框线图和表面图

使用网格数据生成的三维图表还有框线图和表面图。这两种图表将网格数据投射到特定的三维表面，能够使得结果图像非常直观和具有说服力。下面是一个框线图的例子：

    fig = plt.figure()
    ax = plt.axes(projection='3d')
    ax.plot_wireframe(X, Y, Z, color='black')
    ax.set_title('wireframe')

表面图类似框线图，区别在于每个框线构成的多边形都使用颜色进行了填充。添加色图用于填充多边形能够让图形表面展示出来

    ax = plt.axes(projection='3d')
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
                    cmap='viridis', edgecolor='none')
    ax.set_title('surface')

注意虽然每个颜色填充的表面都是二维的，但是表面的边缘不需要是直线构成的。下面的例子使用surface3D绘制了一个部分极坐标网格，能够让我们切入到函数内部观察效果：

	r = np.linspace(0, 6, 20)
    theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
    r, theta = np.meshgrid(r, theta)
    
    X = r * np.sin(theta)
    Y = r * np.cos(theta)
    Z = f(X, Y)
    
    ax = plt.axes(projection='3d')
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
                    cmap='viridis', edgecolor='none')

5.4表面三角剖分

在一些应用场合中，上面的这种均匀网格绘制的图表方式太过于局限和不方便。在这些情况下，三角剖分的图表可以派上用场。如果我们并不是使用笛卡尔坐标系或极坐标系的网格来绘制三维图表，而是使用一组随机的点来绘制三维图表呢？

   theta = 2 * np.pi * np.random.random(1000)
    r = 6 * np.random.random(1000)
    x = np.ravel(r * np.sin(theta))
    y = np.ravel(r * np.cos(theta))
    z = f(x, y)
    
    # 有了上面的数据之后，我们可以使用它们来绘制一张散点图表现出样本所在表面的情况：
    ax = plt.axes(projection='3d')
    ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5)

上图并未形象的表示出表面情况。这种情况下我们可以使用ax.plot_trisurf函数，它能首先根据我们的数据输入找到各点内在的三角函数形式，然后绘制表面（注意的是这里的 x，y，z 是一维的数组）：

    ax = plt.axes(projection='3d')
    ax.plot_trisurf(x, y, z,
                  cmap='viridis', edgecolor='none')

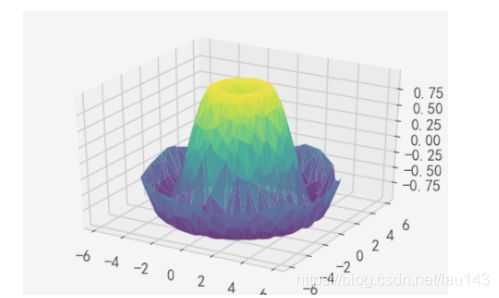上图的结果很显然没有使用网格绘制表面图那么清晰，但是对于我们并不是使用函数构建数据样本（数据样本通常来自真实世界的采样）的情况下，这能提供很大的帮助。例如我们下面会看到，能使用这种方法绘制一条三维的莫比乌斯环。