牛客寒假算法集训营第六场补题题解
网址:https://ac.nowcoder.com/acm/contest/9986
G机器人
知识点:状压dp+__int128
__int128精度比unsigned longlong 大,但是对于cin,cout,printf,scanf都不支持,输入输出模板如下:
inline __int128 read(){
//输入模板
__int128 x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
inline void print(__int128 x){
//输出模板
if(x<0){
putchar('-');
x=-x;
}
if(x>9) print(x/10);
putchar(x%10+'0');
}
代码:
#includeE网格
知识点:动态规划
题解:dp,另外阅读理解?,题目看了半天没看懂。
选择两个,左右和上下各选择一次,可以进行两次dp。
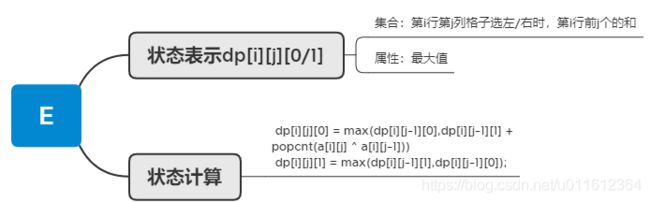
上下时同理
代码:
#includeF组合数
知识点:二项式定理,逆元,数学,虚数快速幂
题解:奇数项/偶数项多项式系数的和2^(n-1) ,要得到题目的式子需要构造式子然后抵消,这个题目中需要引入虚数,就是一个涉及到虚数的快速幂。
最终得到的式子是一份分数,分母为4,题目中又要求了取余,取模运算对于分数不成立,所以需要用到逆元,求4对mod的逆元。
逆元的两种方法;
1、费马小定理(有限制)
p为素数时,a关于mod p的逆元为a^(p-2)mod p。用快速幂模。
但是实际上在acm中题目给的p基本都是质数,所以这是最好用的啦
代码:
#include2、扩展欧几里得(普遍使用的求逆元方法)
#includeB系数
知识点:数学,lucas定理
题解:
虽然但是,我并没有学过lucas定理,那么先从lucas定理开始。
Lucas定理是用来求 C(n,m) mod p,p为素数的值。(p最大1e5左右)
排列组合有一个关系: C n m = C n − 1 m + C n − 1 m − 1 C_n^m = C_{n - 1}^m + C_{n - 1}^{ m - 1} Cnm=Cn−1m+Cn−1m−1
就是可以递推,但是当n,m很大时就不行了。
n,m,p都很大时,Lucas定理用来解决大组合数求模。

上图是个啥东西反正我是看不懂的,在acm中运用主要就是: C n m % p = C n / p m / p ∗ C n % p m % p % p C_n^m \% p = C_{n / p}^{ m / p} * C_{n\%p} ^{m\%p} \% p Cnm%p=Cn/pm/p∗Cn%pm%p%p
对于C(n / p, m / p),如果n / p 还是很大,可以递归下去,一直到世界的尽头,也就是,一个递归。
代码也是非常简单:
ll lucas(ll n,ll m){
if(m==0)
return 1;
return (C(n%p,m%p)*lucas(n/p,m/p))%p;
}
这个题目由于系数要模三,所以在式子中增减3的倍数对答案没有影响, x 2 + x + 1 − 3 x x^2+x+1-3x x2+x+1−3x,变成 ( x − 1 ) 2 (x-1)^2 (x−1)2 ,多项式变为 ( x − 1 ) 2 n (x-1)^{2n} (x−1)2n,k项系数为 C n k x 2 n − k ( − 1 ) k C_n^k x^{2n-k}(-1)^k Cnkx2n−k(−1)k
代码:
#includeH动态最小生成树
知识点:最小生成树,并查集,线段树,归并
暴力解法:
这个题数据不够ok,可以暴力卡过。直接kruskal,查询的时候重新存一下每次查询的范围的边,然后跑最小生成树。写的时候被一个等号卡了一小时+,太惨了。
代码:
#include然后是正解
由于查询是在一个连续的范围内查询,可以联想到需要一个线段树优化。
用线段树维护点l到点m的最小生成树构成的边,线段树每次从子树中,找最小的加入,用并查集判断是否成环,如果成环就放弃加入,相当于每次合并为父节点都是在用kruskal。
建树完成后,就可以快速完成单点更新,同样更新后pushup更新对于区间新的最小生成树权值。
查询的时候类似于归并,将范围内线段树维护的最小生成树的边归并为一个ans数组,由于有n个点,最小生成树一定需要n-1条边,不符合输出impossible,符合输出答案。
#include