可变神经网络 Python代码

可变神经网络 Python代码

这回写一个关于神经网络的代码，博主对于深度学习也是学了很久，学理论的时候，感觉可能神经网络也是中规中矩的的，但是真的自己去写了一个神经网络，并针对一个案例进行测试时，才发现神经网络并没想的那么简单。

这里博主有两个自己最大的体会，给那些没有亲自调过网络的人

1. 学习率非常重要，决定能否收敛
2. 参数初始化很重要，决定是否能找到最优解

话不说我写了一个可变神经网络，读者可以，我在代码中写了注释，如果想要调节网络结构，非常简单，只要改一个列表即可

我对一些核心代码写上了注释，如有疑问，可以在在博客上留言

代码如下：

import numpy as np

import os
import matplotlib.pyplot as plt
def loaddataset(filename):
	fp = open(filename)
 
	#存放数据
	dataset = []
 
	#存放标签
	labelset = []
	for i in fp.readlines():
		a = i.strip().split()
 
		#每个数据行的最后一个是标签
		dataset.append([float(j) for j in a[:len(a)-1]])
		labelset.append(int(float(a[-1])))
	return dataset, labelset

path="E:/BP神经网络/horseColicTraining.txt"
dataset,labelset= loaddataset(path)


 
def sigmoid(z):
	return 1 / (1 + np.exp(-z))


def parameter_initialization(size):
    W=[]  #网络权重
    B=[]  #网络阈值
    for i in range(len(size)-1):
        W.append(np.random.uniform(-0.5, 0.5, (size[i], size[i+1])).astype(np.float64))
        B.append(np.random.uniform(-0.5, 0.5, (1, size[i+1])).astype(np.float64))

    #value1 = np.random.randint(-5, 5, (1, y)).astype(np.float64)
    #value2 = np.random.randint(-5, 5, (1, z)).astype(np.float64)
    #weight1 = np.random.randint(-5, 5, (x, y)).astype(np.float64)
    #weight2 = np.random.randint(-5, 5, (y, z)).astype(np.float64)
    return  W,B

size=[len(dataset[0]),20,20,1]#模型网络层数参数，第一个是输入向量大小，最后一个是输出长度
W,B=parameter_initialization(size)

print(labelset)
print(W)
print("b：  ")
print(B)
print(W[0].shape,len(B[0]))
def foward(x,W,B):#前向传播结果
   # print(np.dot(x,w[0]),b[0])
    o1=x
    o=[]
    for i in range(len(W)):
        o1=sigmoid(np.dot(o1,W[i])+B[i])
        o.append(o1)
       # o2=sigmoid(np.dot(o1,w[i])+b[i])
  #  print(w,b)
    return o
#print(len(labelset))  299
learn_rating=0.0001  #学习率

loss_sum=[]
precision=[]
def  BP(learn_rating,dataset,output,labelset,W,B):
    W_c=[]
    B_c=[]
    for i in W:
         W_c.append(np.zeros_like(i))
    
    for i in B:
         B_c.append(np.zeros_like(i))

    weight2_c=np.zeros_like(W[1])
    weight1_c=np.zeros_like(W[0])
    value2_c=np.zeros_like(B[1])
    value1_c=np.zeros_like(B[0])

    p=0
    for input in dataset[0:100]:

        zz=foward(input,W,B)

        output = [np.mat(input).astype(np.float64)]
        output.extend(zz)
        y=labelset[p]
     #   print(y)
        p=p+1
        a = np.multiply(1 - output[-1],output[-1] )
        g = np.multiply(a, output[-1]-y)
        weight2_change = learn_rating * np.dot(np.transpose(output[-2]), g)
        value2_change = learn_rating * g
        W_c[-1]=W_c[-1]+weight2_change
        B_c[-1]=B_c[-1]+value2_change
       # weight2_c=weight2_c+weight2_change
        #value2_c=value2_c+value2_change
        e=g
        for i in range(len(W)-1):
           # print(i)
            b = np.dot(e, np.transpose(W[len(W)-1-i]))
            c = np.multiply(output[-2-i], 1 - output[-2-i])
            e = np.multiply(b, c)
            value1_change = learn_rating * e
        
            #print(e)
            weight1_change = learn_rating * np.dot(np.transpose(output[-2-i-1]), e)
          #  print(W_c[-2-i].shape,weight1_change.shape)
            W_c[-2-i]=W_c[-2-i]+weight1_change
            B_c[-2-i]=B_c[-2-i]+value1_change
        
        #weight1_c=weight1_c+weight1_change
        
        #value1_c=value1_c+value1_change

    for i in range(len(W)):

        W[i]=W[i]-W_c[i]
    for i in range(len(B)):

        B[i]=B[i]-B_c[i]
   
    loss=0
    pre=0
    p=0
    for i in range(len(dataset)):
        if  foward(dataset[i],W,B)[-1]>0.5  and y==1:
            pre+=1
         #   print(foward(dataset[i],W,B)[-1],labelset[p])
        if  foward(dataset[i],W,B)[-1]<0.5  and y==0:
            pre+=1
        #    print(foward(dataset[i],W,B)[-1],labelset[p])
        p=p+1
        loss=loss+(foward(dataset[i],W,B)[-1]-labelset[i])**2
    #p_y=foward(dataset[0],w,B)

    print(loss/len(dataset))
    print(pre/len(dataset))
    
    loss_sum.append(loss[0][0])
    precision.append(pre)
  #  print(y)

#p=0
#pre=0
#loss=0
#for i in range(len(dataset)):
#        if  foward(dataset[i],W,B)[-1]>0.5  and labelset[p]==1:
#            pre+=1
#            print(foward(dataset[i],W,B)[-1],labelset[p])
#        if  foward(dataset[i],W,B)[-1]<0.5  and labelset[p]==0:
#            print(foward(dataset[i],W,B)[-1],labelset[p])
#            pre+=1
#        p=p+1

#        loss=loss+(foward(dataset[i],W,B)[-1]-labelset[i])**2
#    #p_y=foward(dataset[0],w,B)
#print(loss/len(dataset))
#print(pre/len(dataset))



output=foward(dataset[0],W,B)
print(output)
for i in range(500):
   BP(learn_rating,dataset,output,labelset,W,B)
print()


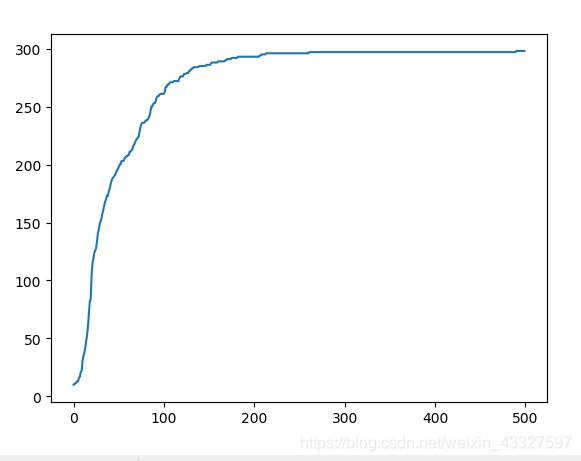
plt.plot(precision)
plt.show()

#plt.plot(loss_sum)
#plt.show()
#print(dataset,labelset)
os.system("pause")