7-1 The Closest Fibonacci Number (20分)
The Fibonacci sequence Fn is defined by Fn+2=Fn+1+Fn for n≥0, with F0=0 and F1=1. The closest Fibonacci number is defined as the Fibonacci number with the smallest absolute difference with the given integer N.
Your job is to find the closest Fibonacci number for any given N.
Input Specification:
Each input file contains one test case, which gives a positive integer N (≤10^8).
Output Specification:
For each case, print the closest Fibonacci number. If the solution is not unique, output the smallest one.
Sample Input:
305Sample Output:
233Hint:
Since part of the sequence is { 0, 1, 1, 2, 3, 5, 8, 12, 21, 34, 55, 89, 144, 233, 377, 610, ... }, there are two solutions: 233 and 377, both have the smallest distance 72 to 305. The smaller one must be printed out.
参考代码:
#include
using namespace std;
int n;
vector fib;
int main(){
scanf("%d", &n);
fib.push_back(0);
fib.push_back(1);
int min_difference = min(abs(n-0), abs(n-1));
int min_num = abs(n-0) < abs(n-1) ? 0 : 1;
int pos = 2;
while(1){
int temp = fib[pos-2] + fib[pos-1];
if(temp - n > min_difference) break;
fib.push_back(temp);
if(abs(temp - n) < min_difference){
min_difference = abs(temp - n);
min_num = temp;
}
pos++;
}
cout << min_num << endl;
return 0;
}
7-2 Subsequence in Substring (25分)
A substring is a continuous part of a string. A subsequence is the part of a string that might be continuous or not but the order of the elements is maintained. For example, given the string atpaaabpabtt, pabt is a substring, while pat is a subsequence.
Now given a string S and a subsequence P, you are supposed to find the shortest substring of S that contains P. If such a solution is not unique, output the left most one.
Input Specification:
Each input file contains one test case which consists of two lines. The first line contains S and the second line P. S is non-empty and consists of no more than 10^4 lower English letters. P is guaranteed to be a non-empty subsequence of S.
Output Specification:
For each case, print the shortest substring of S that contains P. If such a solution is not unique, output the left most one.
Sample Input:
atpaaabpabttpcat
patSample Output:
pabt参考代码:
#include
using namespace std;
int main(){
string seq, check, ans;
int min_len = 10010;
cin >> seq >> check;
int s_len = seq.length();
int c_len = check.length();
for(int i = 0; i < s_len; i++){
if(seq[i] == check[0]){
int pos = 0; //不要从下一位开始,可能会有问题,比如就一个字符
int j = i;
while(j < s_len){
if(seq[j] == check[pos]){
j++;
pos++;
}else j++;
if(pos == c_len && j-i < min_len){
min_len = j-i;
ans = seq.substr(i, j-i); //后一个参数的意义是长度
break;
}
}
}
}
cout << ans << endl;
return 0;
}
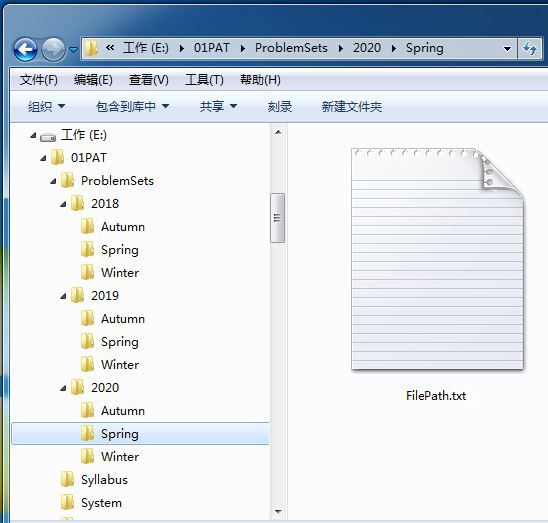
The figure shows the tree view of directories in Windows File Explorer. When a file is selected, there is a file path shown in the above navigation bar. Now given a tree view of directories, your job is to print the file path for any selected file.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤10^3), which is the total number of directories and files. Then N lines follow, each gives the unique 4-digit ID of a file or a directory, starting from the unique root ID 0000. The format is that the files of depth d will have their IDs indented by d spaces. It is guaranteed that there is no conflict in this tree structure.
Then a positive integer K (≤100) is given, followed by K queries of IDs.
Output Specification:
For each queried ID, print in a line the corresponding path from the root to the file in the format: 0000->ID1->ID2->...->ID. If the ID is not in the tree, print Error: ID is not found. instead.
Sample Input:
14
0000
1234
2234
3234
4234
4235
2333
5234
6234
7234
9999
0001
8234
0002
4 9999 8234 0002 6666Sample Output:
0000->1234->2234->6234->7234->9999
0000->1234->0001->8234
0000->0002
Error: 6666 is not found.参考代码:
#include
using namespace std;
struct node{
int dep, order;
};
int n, k;
vector seq;
unordered_map mp;
unordered_map exist;
int main(){
string str;
scanf("%d\n", &n);
for(int i = 0; i < n; i++){
int cot = 0;
getline(cin, str);
for(int j = 0; j < str.length(); j++){
if(str[j] == ' ') cot++;
else break;
}
int num = stoi(str);
seq.push_back(num);
mp[num] = node{cot, i};
exist[num] = 1;
}
scanf("%d", &k);
int check;
for(int i = 0; i < k; i++){
scanf("%d", &check);
if(!exist[check]) printf("Error: %04d is not found.\n", check);
else{
vector ans;
ans.push_back(check);
int now_dep = mp[check].dep - 1;
for(int j = mp[check].order; j >= 0; j--){
if(mp[seq[j]].dep == now_dep){
ans.push_back(seq[j]);
now_dep--;
}
}
for(int j = ans.size()-1; j >= 0; j--) printf("%04d%s", ans[j], j == 0 ? "\n" : "->");
}
}
return 0;
}
7-4 Chemical Equation (30分)
A chemical equation is the symbolic representation of a chemical reaction in the form of symbols and formulae, wherein the reactant entities are given on the left-hand side and the product entities on the right-hand side. For example, CH4+2O2=CO2+2H2O means that the reactants in this chemical reaction are methane and oxygen: CH4 and O2, and the products of this reaction are carbon dioxide and water: CO2 and H2O.
Given a set of reactants and products, you are supposed to tell that in which way we can obtain these products, provided that each reactant can be used only once. For the sake of simplicity, we will consider all the entities on the right-hand side of the equation as one single product.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer N (2≤N≤20), followed by N distinct indices of reactants. The second line gives an integer M (1≤M≤10), followed by M distinct indices of products. The index of an entity is a 2-digit number.
Then a positive integer K (≤50) is given, followed by K lines of equations, in the format:
reactant_1 + reactant_2 + ... + reactant_n -> productwhere all the reactants are distinct and are in increasing order of their indices.
Note: It is guaranteed that
- one set of reactants will not produce two or more different products, i.e. situation like
01 + 02 -> 03and01 + 02 -> 04is impossible; - a reactant cannot be its product unless it is the only one on the left-hand side, i.e.
01 -> 01is always true (no matter the equation is given or not), but01 + 02 -> 01is impossible; and - there are never more than 5 different ways of obtaining a product given in the equations list.
Output Specification:
For each case, print the equations that use the given reactants to obtain all the given products. Note that each reactant can be used only once.
Each equation occupies a line, in the same format as we see in the inputs. The equations must be print in the same order as the products given in the input. For each product in order, if the solution is not unique, always print the one with the smallest sequence of reactants -- A sequence { a1,⋯,am } is said to be smaller than another sequence { b1,⋯,bn } if there exists 1≤i≤min(m,n) so that aj=bj for all j It is guaranteed that at least one solution exists. 思路分析: 参考代码:Sample Input:
8 09 05 03 04 02 01 16 10
3 08 03 04
6
03 + 09 -> 08
02 + 08 -> 04
02 + 04 -> 03
01 + 05 -> 03
01 + 09 + 16 -> 03
02 + 03 + 05 -> 08Sample Output:
02 + 03 + 05 -> 08
01 + 09 + 16 -> 03
04 -> 04
再次栽倒在30分的题上,非常伤心。事后反思,感觉有以下原因:
1.还是未能合理选择数据结构来存储并处理所给数据,或是虽然选择了某一种数据结构,也挺合理,但没有自信,导致不敢勇敢地去写代码,犹犹豫豫。
2.对于深搜中的回溯剪枝操作还不是很熟悉,导致虽然也能想到大致的解法,但操作起来一片稀烂,不能正确确定传参、递归边界以及回溯时的相关操作。
再来看看这题的正确思路。首先,本题数据的维度是三维的,即不同生成物 -> 不同反应方程式 -> 需要的不同反应物。因此,选择一个三维的数据结构来存储是必然的,要坚信自己的选择是正确的。但在对三维数据进行处理时,真的很容易搞迷,所以要细心,头脑要清醒。另外结构体里面放置生成物便于输出。
处理输入数据时,在读取生成物时记得先将自己生成自己的方程式加入。然后主要看方程式的处理,详见代码。读取数据完后记得对每一个生成物对应的所有反应式排序,从而后面深搜找到的第一个答案即为最终答案。(数据结构命名也很重要,可以将数组向量map等设为对应名称的简写,成员则命名为全称)
深搜是重头戏,最重要的是回溯。将DFS设置成返回值的函数从而便于回溯。递归思路如下:先看目前的生成物的每一个生成式,若每个反应物均存在,则递归进入下一个生成物,若缺少任一反应物则直接跳过该生成式。向下递归前,先将该反应式存入答案向量中,然后将对应反应物消耗。递归出来时,要看该路径是否成功找到符合答案的解,若成功则直接返回真。否则:将反应物恢复,且将该反应式从答案向量中弹出,循环进入下一个反应式。所有反应式遍历完均未找到时,则最后返回假。递归边界就是当前生成物不存在,也即已经遍历完所有给定生成物。
综上可见,细节处理比较多,任何一个环节不熟悉都会没有继续下去的信心与勇气,因此后面应该加强复杂问题的求解训练,即短时间考虑诸多因素,选择合理数据结构。#include