python剑指offer系列-leetcode剑指offer系列专题

03. 数组中重复的数字 简单

题目链接
分析
题目难度为简单，最直白的方法就是开辟哈希表记录访问过的数字。
此题可以做到$O(1)$，利用题目中的信息，一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。
假设n为5，按照题意给定一个没有重复数字的数组

index	0	1	2	3	4
data	3	1	4	2	0

可以看到，数据本身是索引的一个置换（题目给的信息），数据本身也可以当索引来用
一个有重复数字的数组

index	0	1	2	3	4
data	3	4	4	0	2

如果把数据当索引来用，一定会出现重复访问，要做的就是记录已经访问的数据。
code

class Solution:
    def findRepeatNumber(self, nums: List[int]) -> int:
        for i in range(len(nums)):
        	# i是原索引，abs(nums[i])是数据，这里当作新索引来用
        	# 若出现重复访问，返回答案
            if nums[abs(nums[i])] < 0:
                return abs(nums[i])
            else:
            	# 次数使用原数据的负数来表示，该数据已经被访问
                nums[abs(nums[i])] = -1 * nums[abs(nums[i])]
        # 到了这一步，重复数字是一定0
        return 0

04. 二维数组中的查找

分析
没啥可讲的，想通了就通了
code

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix or not matrix[0]:
            return False
        rowIndex, colIndex = 0, len(matrix[0])-1
        while rowIndex < len(matrix) and colIndex >=0:
            if matrix[rowIndex][colIndex] == target:
                return True
            elif matrix[rowIndex][colIndex] > target:
                colIndex -= 1
            else:
                rowIndex += 1
                
        return False

07. 重建二叉树

分析
给定前序遍历和中序遍历的结果能确定一颗唯一的二叉树。
关键在于能根据二叉树的前序遍历和中序遍历，确定左右子树的前序遍历和中序遍历。code时唯一要注意的就是何时递归结束。
code

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if not preorder:
            return None
       
        def zp_buildTree(preorder: list, pr_l, pr_r, inorder: list, in_l, in_r):
            if pr_l > pr_r or in_l > in_r:
                return None

            root = TreeNode(preorder[pr_l]) # 构建根结点
            root_index = inorder.index(preorder[pr_l])  # 找到根结点在中序的位置
            L = root_index - in_l
            R = in_r - root_index # 左右子树的长度

            root.left = zp_buildTree(preorder, pr_l+1, pr_l+L, inorder, in_l, root_index-1)
            root.right = zp_buildTree(preorder, pr_l+L+1, pr_r, inorder, root_index+1, in_r)
            return root

        return zp_buildTree(preorder, 0, len(preorder)-1, inorder, 0, len(inorder)-1)

08：二叉树的下一个节点

牛客
分析
这里题目要求是中序遍历（左中右）的下一个节点。
不用关系p是否有左子树，中序遍历中，p的左子树一定都在p前面
给定节点p，若p有右子树，p在中序遍历中的下一个节点就是自己右子树中序遍历结果的第一个节点。
若p没有右子树，那么p右两种可能：
1，p是某棵子树的左子树，p在中序遍历中的下一个节点就是自己的父节点
2，p是某棵子树的右子树，这就要一直向上寻找p的父节点，祖父节点等等（广义上都是父节点）。何时截止，直到当前这个父节点表示的子树是某棵树的左子树，那么下一个父节点就是p在中序遍历中的下一个节点。
使用非递归算法中序遍历遍历一遍二叉树，这个过程就很清楚了。
code

class Solution:
    def GetNext(self, p):
        # write code here
        if p.right:
            p = p.right
            while p.left:
                p = p.left
            return p 
        while p.next and p.next.right == p:
            p = p.next
        return p.next

09-1. 用两个栈实现队列

分析
这里的栈，只支持栈尾 push 和 pop，python的列表虽然有pop(0)这个功能，但这里不能用。
code

class CQueue:

    def __init__(self):
        self.stack1 = []
        self.stack2 = []


    def appendTail(self, value: int) -> None:
        self.stack1.append(value)


    def deleteHead(self) -> int:
        if not self.stack1 and not self.stack2:
            return -1
        elif self.stack2:
            return self.stack2.pop()
        else:
            while self.stack1:
                self.stack2.append(self.stack1.pop())
            return self.stack2.pop()



# Your CQueue object will be instantiated and called as such:
# obj = CQueue()
# obj.appendTail(value)
# param_2 = obj.deleteHead()

09-2：用队列实现栈

code
leetcode225

class MyStack:

    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.q1 = []
        self.q2 = []


    def push(self, x: int) -> None:
        """
        Push element x onto stack.
        """
        self.q1.append(x)
        while self.q2:
            self.q1.append(self.q2.pop(0))
        self.q1, self.q2 = self.q2, self.q1


    def pop(self) -> int:
        """
        Removes the element on top of the stack and returns that element.
        """
        return self.q2.pop(0)


    def top(self) -> int:
        """
        Get the top element.
        """
        return self.q2[0]


    def empty(self) -> bool:
        """
        Returns whether the stack is empty.
        """
        return False if self.q2 else True



# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()

10- I. 斐波那契数列

分析
本题本身难度不大

f = [0] * n
f[0], f[1] = 0, 1
for i in range(2, n+1):
	f[i] = f[i-1] + f[i-2]
return f[n]

重要的在于不必要的空间浪费，本题完全可以做到空间复杂度O(1)
code

class Solution:
    def fib(self, n: int) -> int:
        if n in [0, 1]:
            return n
        a, b = 0, 1
        mod = 1000000007
        for i in range(2, n+1):
            a, b = b, a+b
        return int(b%mod)

10- II. 青蛙跳台阶问题

code

class Solution:
    def numWays(self, n: int) -> int:
        prev, cur = 0, 1
        mod = 1000000007
        for i in range(1, n+1):
            prev, cur = cur, prev+cur
        return int(cur%mod)

11. 旋转数组的最小数字

这题要先看一下leetcode153题leetcode153

153. 寻找旋转排序数组中的最小值

分析
这题意思就是给你一个递增的数组，然后从中间切断数组，再把前半截接在后半截。

原数据是单调递增的，反转后就变成下面所示了，反转后，前半截的数据都大于等于后半截，前后半截各自单调递增。
最小的数就是反转后，后半截的第一个数字，也就是前后半截的分界点。
code

class Solution:
    def findMin(self, nums: List[int]) -> int:
        if nums[0] < nums[-1]:
            return nums[0]
        l, r = 0, len(nums)-1
        while l < r:
            mid = l+r >> 1
            if nums[mid] >= nums[0]:
                l = mid + 1
            else:
                r = mid
        return nums[l]

分析
本题相对于题目153复杂了一点，因为数据不再是纯粹的单调递增，而是包含的相等的值。

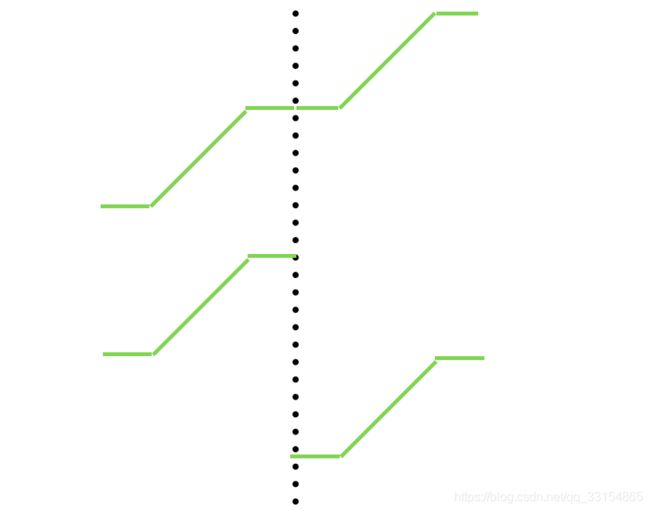
结合153 的答案，在看看本题，实质都是在找前后半截的分界点。
code

class Solution:
    def minArray(self, nums: List[int]) -> int:
        if len(nums) == 1:
            return nums[0]
        if len(nums) == 2:
            return min(nums[0],nums[-1])
        if nums[0] < nums[-1]:
            return nums[0]
        l, r = 0, len(nums)-1
        mid = 0
        while nums[l] >= nums[r]:
            mid = l+r >> 1
            if r - l == 1:
                mid = r
                break
            if nums[mid] == nums[l] and nums[mid] == nums[r]:
                return min(nums[l:r+1])
            elif nums[mid] >= nums[l]:
                l = mid
            elif nums[mid] <= nums[r]:
                r = mid
        return nums[mid]

12. 矩阵中的路径

分析
本题是一道很经典的回溯算法题。题目给的数据量在1到100之间，所以即便时间复杂度达到$O(n^3)$依然不会超时。
最暴力的解法就是罗列出所有的路径，在看看有没有等于word的路径，本题的解法本质上就是这么暴力，不过做了合适的剪枝后就能降低时间复杂度。
矩阵中的每一个点都可以作为起始点，现在我们只看一个点。
现在定义问题就是以 i,j 为起始点寻找路径word，假设$board[i][j]==word[0]$，我们的原问题就变成了四个子问题

• 以 i-1,j 为起始点寻找路径word[1:]
• 以 i,j+1为起始点寻找路径word[1:]
• 以 i+1,j 为起始点寻找路径word[1:]
• 以 i,j-1 为起始点寻找路径word[1:]
  四个子问题只要有一个返回True，我们的原问题就返回True
  code

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        row, col = len(board), len(board[0])
        visited = [[0] * col for _ in range(row)]

        # 四个方向，看个人习惯怎么写
        dx = [-1, 0, 1, 0]
        dy = [0, 1, 0, -1]

        def dfs(x, y, u):
        	# u 表示word[:u](左闭右开)已经找到
        	# board[x][y]==word[u-1]
        	# 现在的子问题就是在 x, y 的四个方向找word[u:]
            if u == len(word):
                return True
            visited[x][y] = 1
            
            # 开始看四个方向，解子问题
            for i in range(4):
                a, b = x+dx[i], y+dy[i]
                # 这长长的一段是剪枝，避免不必要的dfs
                if 0<=a<row and 0<=b<col and not visited[a][b] and board[a][b]==word[u]:
                	# board[a][b]==word[u]
                	# 这个子问题可以继续dfs，此时要标记visited[a][b]已经访问
                	# 在dfs里标记里a,b
                    if dfs(a, b, u+1):
                    	# 只要有一个子问题成功，就可以了
                        return True
            
            # 非常重要的一步，记得回溯，不然其他起始点就失效了
            visited[x][y] = 0
            return False
        
        for i in range(row):
            for j in range(col):
            	# 每个 i,j都可以作为起始点
                if board[i][j] == word[0]:
                    if dfs(i, j, 1):
                        return True
        return False

15. 二进制中1的个数

分析
本题考察的是位运算，很简单的。

bit = x & 1

bit为1，则表示x的二进制的最后一位是1
bit为0，则表示x的二进制的最后一位是0

建议去深入了解一下 原码、反码、补码，会有很多有意思的知识。
code

class Solution:
    def hammingWeight(self, n: int) -> int:
        ans = 0
        x = n
        while x:
            if x & 1:
                ans += 1
            x >>= 1
        return ans

29. 顺时针打印矩阵

分析
这题咋一看有点东西，仔细想想，就是一个线性遍历，$O(n)$。我们把矩阵当作图来看，每个元素是图的一个节点
它的步骤就是：

• 取当前节点
• 找到下一个节点（下一个节点有且只有一个或者没有）继续遍历
• 直到没有下一个节点
  要花点心思的地方就是寻找下一个节点，在矩阵里面就是“拐弯”
  [ 1, 2, 3 ],
  [ 4, 5, 6 ],
  [ 7, 8, 9 ]
  返回1 2 3 6 9 8 7 4 5
  一共有四次拐弯，有三次发生在3 9 7，因为碰到矩阵边界了，还有一次拐弯发生在4，虽然没有碰到边界，但是4的下一个节点1，已经访问过了，只能选择拐弯。
  这种在矩阵里遍历的题目，脑子里一定要有一个直角坐标系
  我习惯使用的坐标系，x正轴向下，y正轴向右。和数学上常用的x正轴向右，y正轴向上不同

x, y
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
# 向右移动
x+dx[1], y+dy[1]
# 上
x+dx[0], y+dy[0]
# 其他同理

看案例
在第一行向右移动x+dx[1], y+dy[1]，
然后向下x+dx[2], y+dy[2]，
接着向左x+dx[3], y+dy[3]，
然后向上x+dx[0=4%4], y+dy[0=4%4]，
最后又是向右x+dx[1], y+dy[1]
code

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix or not matrix[0]:
            return []

        row, col = len(matrix), len(matrix[0])
        ans = []
        visited = [[0]*col for _ in range(row)]

        # 四个方向
        dx = [-1, 0, 1, 0]
        dy = [0, 1, 0, -1]

        def dfs(x, y, d, k):
        	# 遍历 row*col次后，就结束了
            if k == row * col:
                return
            ans.append(matrix[x][y])
            visited[x][y] = 1
            # 准备遍历下一个节点
            a, b = x+dx[d], y+dy[d]
            # 若下一个节点不合法，就要拐弯了
            if not 0<=a<row or not 0<=b<col or visited[a][b]:
            	# 更新d
                d = (d+1)%4
                a, b = x+dx[d], y+dy[d]
            # 其实在本题中，拐弯后下一个节点一定合法，因为只有一种路径
            dfs(a, b, d, k+1)
        dfs(0,0,1,0)
        return ans
            

39. 数组中出现次数超过一半的数字

分析
这题肯定是要通过计数的方式来得到答案了，关键在于如何$O(1)$。本体给的测试用例一定是有解的，解题思路：任意两个不一样的数据点可以相互抵消。

index	0	1	2	3	4
data	a	a	b	b	b

前面的aabb会抵消掉，只剩下b

index	0	1	2	3	4
data	b	b	a	b	b

a会和任意一个b抵消，剩下b
code

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
    	# count表示当前有多少个ans
        ans, count = None, 0
        for num in nums:
            if ans == num:
                count += 1
            elif count > 0:
            	# 不管新数字是多少，它和ans不一样，就抵消掉一个ans
                count -= 1
            else:
            	# 假如ans已经抵消完了，新数字和ans还是不一样，那么，新的ans诞生了  例如aabb b里的最后一个b
                ans, count = num, 1
        return ans

55 - I. 二叉树的深度

分析
当作复习一下大学知识吧
code

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

55 - II. 平衡二叉树

分析
假设你会求树的高度，这题就是让你判断一颗树是不是平衡二叉树。
唯一要注意的就是避免不必要的计算，当你在计算树的高度的时候，起始你也计算它每棵子树的高度，只是没有记录下来。

只要有一棵子树不是平衡的，那这棵树就不是平衡的
code

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:

        def height(root):
            if not root:
                return 0
            left = height(root.left)
            right = height(root.right)
			
			# 不看这个判断语句，height就是在求树的高度
			# 当树是一颗平衡二叉树的时候，该if语句就不会被触发
            if left<0 or right<0 or abs(left-right)>1:
                return -1

            return max(left, right) + 1
        return height(root) >= 0

67. 把字符串转换成整数

分析
跟着代码一起分析吧
code

class Solution:
    def strToInt(self, strn: str) -> int:
    	# 答案要求的数据范围是int32大小
        INT_MIN = -2147483648
        INT_MAX = 2147483647
        num, sign = 0, 1
        l = len(strn)
        # 空字符串 返回0
        if not l:
            return 0
            
        i = 0
        # 排除前面的空格 ‘ ’部分
        while strn[i] == ' ':
            i += 1
            # 若字符串全是空格，返回0
            if i == l:
                return 0
		# 现在i指向字符串第一个非空格字符
		# 再看看 正负符号
        if strn[i] == '+':
            i += 1
        elif strn[i] == '-':
            sign = -1
            i += 1

		# 现在i指向字符串第一个数字字符
        while i < l:
        	# 碰到第一个非数字字符，就结束
            if strn[i] < '0' or strn[i] > '9':
                break
            ##############剪枝开始########
            # 答案要求的数据范围是int32大小
            if num > INT_MAX // 10:
                if sign == 1:
                    return INT_MAX
                else:
                    return INT_MIN
            if num == INT_MAX // 10 and int(strn[i]) > 7:
                if sign == 1:
                    return INT_MAX
                else:
                    return INT_MIN
			#############剪枝结束########
			# 即使不剪枝，计算结果也没问题（时间肯能会超时），自己最后要看看结果有没有越界
			# 剪枝可以提前结束计算
            num = num * 10 + int(strn[i])
            i += 1
        return num * sign

68 - I. 二叉搜索树的最近公共祖先

分析
想假设题目给的$p,q$，$p.val<=q.val$，因为是二叉搜索树，它们的最近公共祖先$root$ 一定满足$p.val<=root.val<=q.val$。
这里面已经包含了答案$root$是$p$或$q$的可能，$p$或$q$也有可能互为根结点。
code

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root:
            return None
        
        def dfs(root, p, q):
            # p.val <= q.val
            if not root:
                return None
            if p.val <= root.val <= q.val:
                return root
            elif root.val < p.val:
                return dfs(root.right, p, q)
            else:
                return dfs(root.left, p, q)
        # 题目给的p q，大小要自己判断一下
        if p.val <= q.val:
            return dfs(root, p, q)
        else:
            return dfs(root, q, p)

68 - II. 二叉树的最近公共祖先

分析
承接上一题，答案$root$有可能是$p$或$q$
在二叉搜索树中，当$p$或$q$不是当前$root$时，$p$和$q$只能同时出现在$root$的左边或右边。
在本题中，还多了第三种可能，当$p$或$q$不是当前$root$时，$p$和$q$还有可能分别现在$root$子树中（不分左右子树）。
code

class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root or not p or not q:
            return None
        if root.val == p.val or root.val == q.val:
            return root
		# p或q不是当前root时，在子树里寻找p或q
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)

        if left and right:
            # p q分别在root的两个子树中
            return root
        # p q同时在一棵子树中
        if not left:
            return right
        else:
            return left