BP反向传播矩阵推导图示详解
该文是我投稿于PaperWeekly的一篇文章,如果大家有什么问题想要跟我讨论,可以留言跟我一起交流。
背景介绍
BP(反向传播)是有Geffrey Hinton在1988年发表的论文《Learning
representations by back-propagating errors》中首次被提出来。该论文从题目到内容到参考文献一共2页半,Hitton也借此工作荣获2018年的图领奖。在深度学习领域,BP的重要程度在怎么强调也不为过,本文会从矩阵的视角对BP下进行详细的推导,为了更好的理解BP的工作原理,本文也画了大量的示意图帮助理解。本文的公式经过自己很多次的推导打磨,尽力做到准确无误,每一张图也是反复的捉摸力求精准表达。本文的阅读难度确实很大,但是因为其重要,我觉得反复抄写下面的推导,也会有很多收获。
引言
在吴恩达的斯坦福机器学习的讲义中关于BP原理的介绍只给出了最后的BP矩阵的推导结果,略去了中间的推导过程。本文会对略去的推导过程进行补全。为了减少阅读阻碍,BP矩阵证明过程会从预备知识开始慢慢铺展开来,其中最难啃的部分就是矩阵形式的链式法则。本文文章结构和的各个章节的内容如下:
-
预备知识介绍了矩阵求导的细节,如果想要看懂之后的BP矩阵推导这部分的两个小节一定要看明白
-
4层无激活函数的BP推导细节
-
L层无激活函数的BP推导细节
-
4层含激活函数的BP推导细节
-
L层含激活函数的BP推导细节
-
吴恩达机器学习讲义中关于BP章节结果的验证
预备知识
推导形式1
F s ( θ ) = ∣ ∣ Y − U V X ∣ ∣ 2 (1) \tag{1} F_s(\theta) = ||Y-UVX||^2 Fs(θ)=∣∣Y−UVX∣∣2(1)
已知, F s ( θ ) F_s(\theta) Fs(θ)是标量即 F s ( θ ) ∈ R 1 × 1 F_s(\theta) \in \mathbb{R}^{1 \times 1} Fs(θ)∈R1×1, Y ∈ R m × 1 Y \in \mathbb{R}^{m \times 1} Y∈Rm×1, U ∈ R m × k U \in \mathbb{R}^{m \times k} U∈Rm×k, V ∈ R k × n V \in \mathbb{R}^{k \times n} V∈Rk×n, X ∈ R n × 1 X \in \mathbb{R}^{n \times 1} X∈Rn×1, ∣ ∣ . ∣ ∣ 2 ||.||^2 ∣∣.∣∣2表示向量的2范数,将矩阵中各个维度带入到公式 ( 1 ) (1) (1)有如下形式:
F s ( θ ) 1 × 1 = ∣ ∣ Y m × 1 − U m × k V k × n X n × 1 ∣ ∣ 2 (2) \tag{2} F_s(\theta)_{1 \times 1} = ||Y_{m \times 1}-U_{m \times k}V_{k \times n}X_{n \times 1}||^2 Fs(θ)1×1=∣∣Ym×1−Um×kVk×nXn×1∣∣2(2)令 e m × 1 = Y m × 1 − U m × k V k × n X n × 1 e_{m \times 1}=Y_{m \times 1}-U_{m \times k}V_{k \times n}X_{n \times 1} em×1=Ym×1−Um×kVk×nXn×1, F s ( θ ) 1 × 1 = e 1 × m T e m × 1 F_s(\theta)_{1 \times 1} = e_{1 \times m}^{\mathrm{T}}e_{m \times 1} Fs(θ)1×1=e1×mTem×1。则对矩阵 V V V的链式法则的求导公式如下所示: ∂ F s ( θ ) ∂ V = ∂ F s ( θ ) ∂ e ⊙ ∂ e ∂ V = − 2 U k × m T e m × 1 X 1 × n T (3) \tag{3} \frac{\partial F_s(\theta)}{\partial V} = \frac{\partial F_s(\theta)}{\partial e} \odot \frac{\partial e}{\partial V} = -2 U_{k \times m}^{\mathrm{T}}e_{m \times 1}X_{1 \times n}^{\mathrm{T}} ∂V∂Fs(θ)=∂e∂Fs(θ)⊙∂V∂e=−2Uk×mTem×1X1×nT(3)其中 ∂ F s ( θ ) ∂ V ∈ R k × n \frac{\partial F_s(\theta)}{\partial V} \in \mathbb{R}^{k \times n} ∂V∂Fs(θ)∈Rk×n, U k × m T e m × 1 X 1 × n T ∈ R k × n U^{\mathrm{T}}_{k \times m}e_{m \times 1}X^{\mathrm{T}}_{1 \times n} \in \mathbb{R}^{k \times n} Uk×mTem×1X1×nT∈Rk×n,直观可以发现等式([3])左右两边的雅可比矩阵维度一致。
对矩阵 U U U的链式法则的求导公式如下所示: ∂ F s ( θ ) ∂ U = ∂ F s ( θ ) ∂ e ⊙ ∂ e ∂ U = − 2 e m × 1 ( V k × n X n × 1 ) T (4) \tag{4} \frac{\partial F_s(\theta)}{\partial U} = \frac{\partial F_s(\theta)}{\partial e} \odot \frac{\partial e}{\partial U} = -2 e_{m \times 1}(V_{k \times n}X_{n \times 1})^{\mathrm{T}} ∂U∂Fs(θ)=∂e∂Fs(θ)⊙∂U∂e=−2em×1(Vk×nXn×1)T(4)其中 ∂ F s ( θ ) ∂ U ∈ R m × k \frac{\partial F_s(\theta)}{\partial U} \in \mathbb{R}^{m \times k} ∂U∂Fs(θ)∈Rm×k, e m × 1 ( V k × n X n × 1 ) T ∈ R m × k e_{m \times 1}(V_{k \times n}X_{n \times 1})^{\mathrm{T}} \in \mathbb{R}^{m \times k} em×1(Vk×nXn×1)T∈Rm×k,等式 ( 4 ) (4) (4)左右两边的雅可比矩阵维度一致。
推导形式2
F s ( θ ) = ∣ ∣ Y − U σ ( V X ) ∣ ∣ 2 (5) \tag{5} F_s(\theta) = ||Y-U\sigma(VX)||^2 Fs(θ)=∣∣Y−Uσ(VX)∣∣2(5)
σ ( ⋅ ) \sigma(\cdot) σ(⋅)是激活函数, F s ( θ ) F_s(\theta) Fs(θ)是标量即 F s ( θ ) ∈ R 1 × 1 F_s(\theta) \in \mathbb{R}^{1 \times 1} Fs(θ)∈R1×1, Y ∈ R m × 1 Y \in \mathbb{R}^{m \times 1} Y∈Rm×1, U ∈ R m × k U \in \mathbb{R}^{m \times k} U∈Rm×k, V ∈ R k × n V \in \mathbb{R}^{k \times n} V∈Rk×n, X ∈ R n × 1 X \in \mathbb{R}^{n \times 1} X∈Rn×1, ∣ ∣ . ∣ ∣ 2 ||.||^2 ∣∣.∣∣2表示向量的2范数,将矩阵的各个维度带入到公式 ( 5 ) (5) (5)中有如下形式:
F s ( θ ) 1 × 1 = ∣ ∣ Y m × 1 − U m × k σ ( V k × n X n × 1 ) ∣ ∣ 2 (6) \tag{6} F_s(\theta)_{1 \times 1} = ||Y_{m \times 1}-U_{m \times k}\sigma(V_{k \times n}X_{n \times 1})||^2 Fs(θ)1×1=∣∣Ym×1−Um×kσ(Vk×nXn×1)∣∣2(6)令 Z k × 1 = V k × n X n × 1 Z_{k \times 1}=V_{k \times n}X_{n \times 1} Zk×1=Vk×nXn×1, A k × 1 = σ ( Z k × 1 ) A_{k \times 1}=\sigma(Z_{k \times 1}) Ak×1=σ(Zk×1), e m × 1 = Y m × 1 − U m × k A k × 1 e_{m \times 1}=Y_{m \times 1}-U_{m \times k}A_{k \times 1} em×1=Ym×1−Um×kAk×1, F s ( θ ) 1 × 1 = e 1 × m T e m × 1 F_s(\theta)_{1 \times 1}=e^{T}_{1 \times m}e_{m \times 1} Fs(θ)1×1=e1×mTem×1,则有
∂ F s ( θ ) ∂ V = ∂ F s ( θ ) ∂ e ⊙ ∂ e ∂ A ⊙ ∂ A ∂ z ⊙ ∂ z ∂ V = − 2 D k × k U k × m T e m × 1 X 1 × n T (7) \tag{7} \frac{\partial F_s(\theta)}{\partial V} = \frac{\partial F_s(\theta)}{\partial e} \odot \frac{\partial e}{\partial A}\odot \frac{\partial A}{\partial z}\odot \frac{\partial z}{\partial V} = -2 D_{k \times k}U_{k \times m}^{\mathrm{T}}e_{m \times 1}X_{1 \times n}^{\mathrm{T}} ∂V∂Fs(θ)=∂e∂Fs(θ)⊙∂A∂e⊙∂z∂A⊙∂V∂z=−2Dk×kUk×mTem×1X1×nT(7)其中, D k × k = d i a g { σ ′ ( V k × n X n × 1 ) } D_{k \times k} = diag\{\sigma^{'}(V_{k \times n}X_{n \times 1})\} Dk×k=diag{ σ′(Vk×nXn×1)},即 D k × k D_{k \times k} Dk×k是一个对角矩阵,对角线的元素为激活函数的导数。 ∂ F s ( θ ) ∂ V ∈ R k × n \frac{\partial F_s(\theta)}{\partial V} \in \mathbb{R}^{k \times n} ∂V∂Fs(θ)∈Rk×n和 D k × k U k × m T e m × 1 X 1 × n T ∈ R k × n D_{k \times k}U_{k \times m}^{\mathrm{T}}e_{m \times 1}X_{1 \times n}^{\mathrm{T}} \in \mathbb{R}^{k \times n} Dk×kUk×mTem×1X1×nT∈Rk×n矩阵的维度一致。
∂ F s ( θ ) ∂ U = ∂ F s ( θ ) ∂ e ⊙ ∂ e ∂ U = − 2 e m × 1 [ σ ( V k × n X n × 1 ) ] T (8) \tag{8} \frac{\partial F_s(\theta)}{\partial U} = \frac{\partial F_s(\theta)}{\partial e} \odot \frac{\partial e}{\partial U} = -2 e_{m \times 1}[\sigma(V_{k \times n}X_{n \times 1})]^{\mathrm{T}} ∂U∂Fs(θ)=∂e∂Fs(θ)⊙∂U∂e=−2em×1[σ(Vk×nXn×1)]T(8)其中, ∂ F s ( θ ) ∂ U ∈ R m × k \frac{\partial F_s(\theta)}{\partial U} \in \mathbb{R}^{m \times k} ∂U∂Fs(θ)∈Rm×k和 e m × 1 [ σ ( V k × n X n × 1 ) ] T ∈ R m × k e_{m \times 1}[\sigma(V_{k \times n}X_{n \times 1})]^{\mathrm{T}} \in \mathbb{R}^{m \times k} em×1[σ(Vk×nXn×1)]T∈Rm×k矩阵的维度一致。
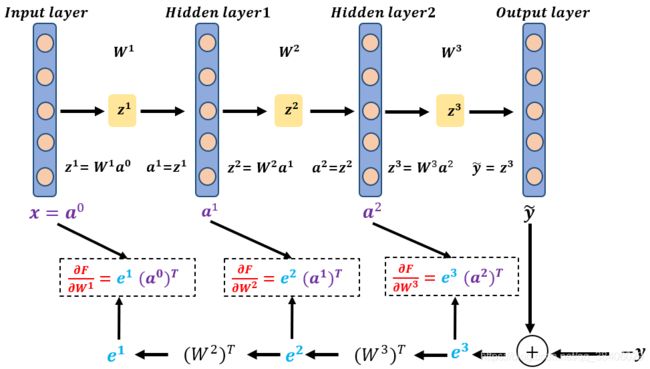
4层无激活函数的神经网络
上图表示的是4层无激活函数神经网络的前向传播过程,其中损失函数如下所示: F s ( θ ) = ∣ ∣ y − y ~ ∣ ∣ 2 = ∣ ∣ y − W 3 W 2 W 1 x ∣ ∣ 2 F_s({\theta})=||y-\tilde{y}||^2=||y-W^{3}W^{2}W^{1}x||^2 Fs(θ)=∣∣y−y~∣∣2=∣∣y−W3W2W1x∣∣2
令 e = y − W 3 W 2 W 1 x e=y-W^{3}W^{2}W^{1}x e=y−W3W2W1x,根据预备知识的推导形式1的公式 ( 3 ) (3) (3), ( 4 ) (4) (4)可求得: ∂ F s ( θ ) ∂ W 3 = − 2 e ( W 2 W 1 x ) T (10) \tag{10} \frac{\partial F_s(\theta)}{\partial W^{3}}=-2 e (W^{2}W^{1}x)^{\mathrm{T}} ∂W3∂Fs(θ)=−2e(W2W1x)T(10) ∂ F s ( θ ) ∂ W 2 = − 2 ( W 3 ) T e ( W 1 x ) T (11) \tag{11} \frac{\partial F_s(\theta)}{\partial W^{2}}=-2(W^{3})^{\mathrm{T}} e (W^{1}x)^{\mathrm{T}} ∂W2∂Fs(θ)=−2(W3)Te(W1x)T(11) ∂ F s ( θ ) ∂ W 1 = − 2 ( W 3 W 2 ) T e x T (12) \tag{12} \frac{\partial F_s(\theta)}{\partial W^{1}}=-2(W^{3}W^{2})^{\mathrm{T}} e x^{\mathrm{T}} ∂W1∂Fs(θ)=−2(W3W2)TexT(12)
令 e 3 = − 2 e e^{3}=-2e e3=−2e, e 2 = ( W 3 ) T e 3 e^{2}=(W^{3})^{\mathrm{T}}e^{3} e2=(W3)Te3, e 1 = ( W 2 ) T e 2 e^{1}=(W^{2})^{\mathrm{T}}e^{2} e1=(W2)Te2。又因为 a 0 = x a^{0}=x a0=x,
a 1 = W 1 x a^{1}=W^{1}x a1=W1x, a 2 = W 2 W 1 x a^{2}=W^{2}W^{1}x a2=W2W1x,将公式([10]),([11]),([12])整理为如下所示: ∂ F s ( θ ) ∂ W 3 = e 3 ( a 2 ) T (13) \tag{13} \frac{\partial F_s(\theta)}{\partial W^{3}}=e^{3} (a^{2})^{\mathrm{T}} ∂W3∂Fs(θ)=e3(a2)T(13) ∂ F s ( θ ) ∂ W 2 = e 2 ( a 1 ) T (14) \tag{14} \frac{\partial F_s(\theta)}{\partial W^{2}}=e^{2} (a^{1})^{\mathrm{T}} ∂W2∂Fs(θ)=e2(a1)T(14) ∂ F s ( θ ) ∂ W 1 = e 1 ( a 0 ) T (15) \tag{15} \frac{\partial F_s(\theta)}{\partial W^{1}}=e^{1} (a^{0})^{\mathrm{T}} ∂W1∂Fs(θ)=e1(a0)T(15)根据公式 ( 13 ) (13) (13), ( 14 ) (14) (14), ( 15 ) (15) (15)将4层无激活函数的BP原理可以形象地表示为下图所示,其中图中虚线框表示为各个层权重参数的梯度,可以发现各层的权重参数梯度由前一层网络的前馈计算值与后一层网络传播的误差信息整合而来。
L层无激活函数的神经网络
上图表示的是L层无激活函数神经网络的前向传播过程,其中损失函数如下所示:
F s ( θ ) = ∣ ∣ y − y ~ ∣ ∣ 2 = ∣ ∣ y − W L − 1 W L − 2 ⋅ ⋅ ⋅ W 2 W 1 x ∣ ∣ 2 F_s({\theta})=||y-\tilde{y}||^2=||y-W^{L-1}W^{L-2} \cdot\cdot\cdot W^{2}W^{1}x||^2 Fs(θ)=∣∣y−y~∣∣2=∣∣y−WL−1WL−2⋅⋅⋅W2W1x∣∣2令 e = y − W L − 1 W L − 2 ⋅ ⋅ ⋅ W 2 W 1 x e = y-W^{L-1}W^{L-2} \cdot\cdot\cdot W^{2}W^{1}x e=y−WL−1WL−2⋅⋅⋅W2W1x,根据预备知识的推导形式1的公式 ( 3 ) (3) (3), ( 4 ) (4) (4)可求得:
∂ F s ( θ ) ∂ W L − 1 = − 2 e ( W L − 2 W L − 3 ⋅ ⋅ ⋅ W 2 W 1 x ) T \frac{\partial F_s(\theta)}{\partial W^{L-1}}=-2 e (W^{L-2}W^{L-3} \cdot\cdot\cdot W^{2}W^{1}x)^{\mathrm{T}} ∂WL−1∂Fs(θ)=−2e(WL−2WL−3⋅⋅⋅W2W1x)T ∂ F s ( θ ) ∂ W i = − 2 ( W L − 1 ⋅ ⋅ ⋅ W i + 1 ) e ( W i − 1 ⋅ ⋅ ⋅ W 1 ) T \frac{\partial F_s(\theta)}{\partial W^{i}}=-2(W^{L-1}\cdot\cdot\cdot W^{i+1})e(W^{i-1}\cdot\cdot\cdot W^{1})^{\mathrm{T}} ∂Wi∂Fs(θ)=−2(WL−1⋅⋅⋅Wi+1)e(Wi−1⋅⋅⋅W1)T ∂ F s ( θ ) ∂ W 1 = − 2 ( W L − 1 W L − 2 ⋅ ⋅ ⋅ W 2 W 1 ) T e x T \frac{\partial F_s(\theta)}{\partial W^{1}}=-2(W^{L-1}W^{L-2}\cdot\cdot\cdot W^{2}W^{1})^{\mathrm{T}} e x^{\mathrm{T}} ∂W1∂Fs(θ)=−2(WL−1WL−2⋅⋅⋅W2W1)TexT令 e L − 1 = − 2 e e^{L-1}=-2e eL−1=−2e, e L − 2 = ( W L − 1 ) T e L − 1 e^{L-2}=(W^{L-1})^{\mathrm{T}}e^{L-1} eL−2=(WL−1)TeL−1, e i = ( W i + 1 ) T e i + 1 e^{i}=(W^{i+1})^{\mathrm{T}}e^{i+1} ei=(Wi+1)Tei+1, e 1 = ( W 2 ) T e 2 e^{1}=(W^{2})^{\mathrm{T}}e^{2} e1=(W2)Te2。又因为 a 0 = x a^{0}=x a0=x, a 1 = W 1 x a^{1}=W^{1}x a1=W1x, a 2 = W 2 W 1 x a^{2}=W^{2}W^{1}x a2=W2W1x, a i = W i W i − 1 ⋅ ⋅ ⋅ W 1 x a^{i}=W^{i}W^{i-1} \cdot\cdot\cdot W^{1}x ai=WiWi−1⋅⋅⋅W1x, a L − 2 = W L − 2 W L − 3 ⋅ ⋅ ⋅ W 1 x a^{L-2}=W^{L-2}W^{L-3} \cdot\cdot\cdot W^{1}x aL−2=WL−2WL−3⋅⋅⋅W1x,则梯度的通项公式为 ∂ F s ( θ ) ∂ W i = e i ( a i − 1 ) T , i = 1 , ⋅ ⋅ ⋅ , L − 1 (20) \tag{20} \frac{\partial F_s(\theta)}{\partial W^{i}}= e^{i} (a^{i-1})^{\mathrm{T}}, i= 1,\cdot\cdot\cdot ,L-1 ∂Wi∂Fs(θ)=ei(ai−1)T,i=1,⋅⋅⋅,L−1(20)
根据公式 ( 20 ) (20) (20)将L层无激活函数的BP原理可以形象地表示为下图所示:
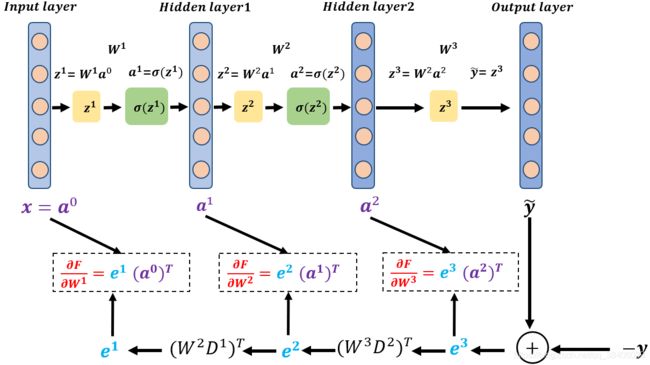
4层含激活函数的神经网络

上图表示的是4层含激活函数神经网络的前向传播过程,其中损失函数如下所示: F s ( θ ) = ∣ ∣ y − y ~ ∣ ∣ 2 = ∣ ∣ y − W 3 σ ( W 2 σ ( W 1 x ) ) ∣ ∣ 2 F_s({\theta})=||y-\tilde{y}||^2=||y-W^{3}\sigma(W^{2}\sigma(W^{1}x))||^2 Fs(θ)=∣∣y−y~∣∣2=∣∣y−W3σ(W2σ(W1x))∣∣2令 e = y − W 3 σ ( W 2 σ ( W 1 x ) ) e = y-W^{3}\sigma(W^{2}\sigma(W^{1}x)) e=y−W3σ(W2σ(W1x)),根据预备知识的推导形式2的公式 ( 7 ) (7) (7), ( 8 ) (8) (8)可求得: ∂ F s ( θ ) ∂ W 3 = − 2 e ( σ ( W 2 σ ( W 1 x ) ) ) T \frac{\partial F_s(\theta)}{\partial W^{3}}=-2 e (\sigma(W^{2}\sigma(W^{1}x)))^{\mathrm{T}} ∂W3∂Fs(θ)=−2e(σ(W2σ(W1x)))T ∂ F s ( θ ) ∂ W 2 = − 2 ( W 3 D 2 ) T e ( σ ( W 1 x ) ) ) T \frac{\partial F_s(\theta)}{\partial W^{2}}=-2 (W^{3}D^{2})^{\mathrm{T}} e (\sigma(W^{1}x)))^{\mathrm{T}} ∂W2∂Fs(θ)=−2(W3D2)Te(σ(W1x)))T ∂ F s ( θ ) ∂ W 1 = − 2 ( W 2 D 1 ) T ( W 3 D 2 ) T e x T \frac{\partial F_s(\theta)}{\partial W^{1}}=-2 (W^{2}D^{1})^{\mathrm{T}} (W^{3}D^{2})^{\mathrm{T}} e x^{\mathrm{T}} ∂W1∂Fs(θ)=−2(W2D1)T(W3D2)TexT其中 D 1 = d i a g { σ ′ ( W 1 x ) } D^1=diag\{\sigma^{'}(W^1x)\} D1=diag{ σ′(W1x)}和 D 2 = d i a g { σ ′ ( W 2 σ ( W 1 x ) ) } D^2=diag\{\sigma^{'}(W^2\sigma(W^1x))\} D2=diag{ σ′(W2σ(W1x))}为对角矩阵,令 e 3 = − 2 e e^{3}=-2e e3=−2e,则有 e 2 = ( W 3 D 2 ) T e 3 e^2=(W^{3}D^{2})^{\mathrm{T}} e^3 e2=(W3D2)Te3, e 1 = ( W 2 D 1 ) T e 2 e^1= (W^{2}D^{1})^{\mathrm{T}} e^2 e1=(W2D1)Te2;令 a 0 = x a^0=x a0=x, a 1 = σ ( W 1 x ) a^1=\sigma(W^1x) a1=σ(W1x) a 2 = σ ( W 2 σ ( W 1 x ) ) a^2=\sigma(W^2\sigma(W^1x)) a2=σ(W2σ(W1x))。综上所述有:
∂ F s ( θ ) ∂ W 3 = e 3 ( a 2 ) T (25) \tag{25} \frac{\partial F_s(\theta)}{\partial W^{3}}=e^{3} (a^{2})^{\mathrm{T}} ∂W3∂Fs(θ)=e3(a2)T(25) ∂ F s ( θ ) ∂ W 2 = e 2 ( a 1 ) T (26) \tag{26} \frac{\partial F_s(\theta)}{\partial W^{2}}=e^{2} (a^{1})^{\mathrm{T}} ∂W2∂Fs(θ)=e2(a1)T(26) ∂ F s ( θ ) ∂ W 1 = e 1 ( a 0 ) T (27) \tag{27} \frac{\partial F_s(\theta)}{\partial W^{1}}=e^{1} (a^{0})^{\mathrm{T}} ∂W1∂Fs(θ)=e1(a0)T(27)根据公式 ( 25 ) (25) (25), ( 26 ) (26) (26), ( 27 ) (27) (27)将4层含激活函数的BP原理可以形象地表示为下图所示,跟4层无激活函数BP原理示意图的差异在于后向传播的误差信息需要多乘一个对角矩阵 D i D^i Di。
L层含激活函数的神经网络

上图表示的是L层含激活函数神经网络的前向传播过程,其中损失函数如下所示: F s ( θ ) = ∣ ∣ y − y ~ ∣ ∣ 2 = ∣ ∣ y − W L − 1 σ ( W L − 2 ⋅ ⋅ ⋅ W 2 σ ( W 1 x ) ⋅ ⋅ ⋅ ) ∣ ∣ 2 F_s({\theta})=||y-\tilde{y}||^2=||y-W^{L-1}\sigma(W^{L-2} \cdot\cdot\cdot W^{2}\sigma(W^{1}x)\cdot\cdot\cdot)||^2 Fs(θ)=∣∣y−y~∣∣2=∣∣y−WL−1σ(WL−2⋅⋅⋅W2σ(W1x)⋅⋅⋅)∣∣2令 e = y − W L − 1 σ ( W L − 2 ⋅ ⋅ ⋅ W 2 σ ( W 1 x ) ⋅ ⋅ ⋅ ) e=y-W^{L-1}\sigma(W^{L-2} \cdot\cdot\cdot W^{2}\sigma(W^{1}x)\cdot\cdot\cdot) e=y−WL−1σ(WL−2⋅⋅⋅W2σ(W1x)⋅⋅⋅),根据预备知识的推导形式2的公式 ( 7 ) (7) (7), ( 8 ) (8) (8)可求得:
∂ F s ( θ ) ∂ W L − 1 = − 2 e ( σ ( W L − 2 ⋅ ⋅ ⋅ W 2 σ ( W 1 x ) ⋅ ⋅ ⋅ ) T \frac{\partial F_s(\theta)}{\partial W^{L-1}}=-2 e (\sigma(W^{L-2} \cdot\cdot\cdot W^{2}\sigma(W^{1}x)\cdot\cdot\cdot)^{\mathrm{T}} ∂WL−1∂Fs(θ)=−2e(σ(WL−2⋅⋅⋅W2σ(W1x)⋅⋅⋅)T ∂ F s ( θ ) ∂ W 1 = − 2 ( W L − 1 D L − 2 ⋅ ⋅ ⋅ W 2 D 1 ) T e x T \frac{\partial F_s(\theta)}{\partial W^{1}}= -2(W^{L-1}D^{L-2} \cdot\cdot\cdot W^{2}D^{1})^{\mathrm{T}} e x^{\mathrm{T}} ∂W1∂Fs(θ)=−2(WL−1DL−2⋅⋅⋅W2D1)TexT ∂ F s ( θ ) ∂ W i = − 2 ( W L − 1 D L − 2 ⋅ ⋅ ⋅ W i + 1 D i ) e ( σ ( W i − 1 ⋅ ⋅ ⋅ W 2 σ ( W 1 x ) ⋅ ⋅ ⋅ ) T \frac{\partial F_s(\theta)}{\partial W^{i}}=-2(W^{L-1}D^{L-2} \cdot\cdot\cdot W^{i+1}D^{i})e (\sigma(W^{i-1} \cdot\cdot\cdot W^{2}\sigma(W^{1}x)\cdot\cdot\cdot)^{\mathrm{T}} ∂Wi∂Fs(θ)=−2(WL−1DL−2⋅⋅⋅Wi+1Di)e(σ(Wi−1⋅⋅⋅W2σ(W1x)⋅⋅⋅)T其中, D i = d i a g { σ ′ ( ⋅ ) } , i = 1 , ⋅ ⋅ ⋅ , L − 1 D^{i}=diag\{\sigma^{'}(\cdot)\},i = 1, \cdot\cdot\cdot, L-1 Di=diag{ σ′(⋅)},i=1,⋅⋅⋅,L−1为对称矩阵。 e L − 1 = − 2 e e^{L-1}=-2e eL−1=−2e,则 e L − 2 = ( W L − 1 D L − 2 ) T e L − 1 e^{L-2}=(W^{L-1}D^{L-2})^{\mathrm{T}}e^{L-1} eL−2=(WL−1DL−2)TeL−1, e i = ( W i + 1 D i ) T e i + 1 e^{i} = (W^{i+1}D^{i})^{\mathrm{T}}e^{i+1} ei=(Wi+1Di)Tei+1, e 1 = ( W 2 D 1 ) T e 2 e^{1}=(W^{2}D^{1})^{\mathrm{T}}e^{2} e1=(W2D1)Te2; a 0 = x a^{0}=x a0=x, a 1 = σ ( W 1 x ) a^{1}=\sigma(W^{1}x) a1=σ(W1x), a i = σ ( W i a i − 1 ) a^{i}=\sigma(W^{i}a^{i-1}) ai=σ(Wiai−1), a L − 2 = σ ( W L − 2 a L − 1 ) a^{L-2}=\sigma(W^{L-2}a^{L-1}) aL−2=σ(WL−2aL−1)。综上所述可知梯度的通项公式为: ∂ F s ( θ ) ∂ W i = e i ( a i − 1 ) T , i = 1 , ⋅ ⋅ ⋅ , L − 1 (32) \tag{32} \frac{\partial F_s(\theta)}{\partial W^{i}}=e^{i} (a^{i-1})^{\mathrm{T}}, i = 1, \cdot\cdot\cdot, L-1 ∂Wi∂Fs(θ)=ei(ai−1)T,i=1,⋅⋅⋅,L−1(32)根据公式 ( 32 ) (32) (32)将L层含激活函数的BP原理可以形象地表示为下图所示:

验证BP矩阵推导
本节主要是对吴恩达机器学习讲义中(ML-AndrewNg-Notes:Coursera)关于BP原理结论部分的验证,所以本文的主要目的是验证吴中的关于BP结论与本文的的结论是否一致。由于符号和表示形式的差异,一个4层的神经网络,具体示意图如下所示:

从最后一层的误差开始计算,误差是激活单元的预测 a k ( 4 ) a^{(4)}_k ak(4)与实际值 y k y_k yk之间的误差。用 δ \delta δ来表示误差,则:
δ ( 4 ) = a ( 4 ) − y (33) \tag{33} \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y(33) 利用误差值 δ ( 4 ) \delta^{(4)} δ(4)来计算前一层的误差: δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) ∗ g ′ ( z ( 3 ) ) (34) \tag{34} \delta^{(3)}=\left(\Theta^{(3)}\right)^{T} \delta^{(4)} * g^{\prime}\left(z^{(3)}\right) δ(3)=(Θ(3))Tδ(4)∗g′(z(3))(34)
其中 g ′ ( z ( 3 ) ) g^{\prime}\left(\mathrm{z}^{(3)}\right) g′(z(3))是 g ( z ( 3 ) ) g\left(\mathrm{z}^{(3)}\right) g(z(3))导数, ( Θ ( 3 ) ) T δ ( 4 ) \left(\Theta^{(3)}\right)^{T} \delta^{(4)} (Θ(3))Tδ(4)是经权重 Θ ( 3 ) \Theta^{(3)} Θ(3)而导致的误差。 第二层的误差为: δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) ∗ g ′ ( z ( 2 ) ) (35) \tag{35} \delta^{(2)}=\left(\Theta^{(2)}\right)^{T} \delta^{(3)} * g^{\prime}\left(z^{(2)}\right) δ(2)=(Θ(2))Tδ(3)∗g′(z(2))(35)因为第一层是输入变量,不存在误差,有了所有的误差表达式之后,便可以计算各个层权重的偏导数为:
∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i ( l + 1 ) (36) \tag{36}\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=a_{j}^{(l)} \delta_{i}^{(l+1)} ∂Θij(l)∂J(Θ)=aj(l)δi(l+1)(36)
l l l代表目前所计算的第几层, j j j代表目前计算层中的激活单元的下标,也是下一层的第 j j j个输入变量的下标。 i i i代表下一层中误差单元的下标,是受到权重矩阵中的第 i i i行影响的下一层中的误差单元的下标。
验证:
吴恩达的这个讲义中关于BP推导中只展示出矩阵推导出的结果,略出了中间证明的部分,其中的证明过程可以类比本文中证明过程,为了能够让验证BP推导过程更清楚,我将吴恩达机器学习讲义中的推导符号与本文中层含激活函数的神经网络的符号进行类比如下表所示:
对比可以发现,验证的重点在于证明 δ ( 4 ) = e 3 \delta^{(4)}=e^{3} δ(4)=e3, δ ( 3 ) = e 2 \delta^{(3)}=e^{2} δ(3)=e2, δ ( 2 ) = e 1 \delta^{(2)}=e^{1} δ(2)=e1。
1)证明: δ ( 4 ) = e 3 \delta^{(4)}=e^{3} δ(4)=e3
因为 δ ( 4 ) \delta^{(4)} δ(4), e 3 e^{3} e3都为最后一层的误差,所以 δ ( 4 ) = e 3 \delta^{(4)}=e^{3} δ(4)=e3,证毕
2)证明: δ ( 3 ) = e 2 \delta^{(3)}=e^{2} δ(3)=e2
由上表几的转换可知: δ ′ ( 3 ) = e 2 = ( W 3 D 2 ) T e 3 = ( D 2 ) T ( Θ ( 3 ) ) T δ ( 4 ) (37) \tag{37} \delta^{'(3)} = e^{2}=(W^{3}D^{2})^{\mathrm{T}} e^3 = (D^{2})^{\mathrm{T}}(\Theta^{(3)})^{\mathrm{T}} \delta^{(4)} δ′(3)=e2=(W3D2)Te3=(D2)T(Θ(3))Tδ(4)(37)
其中, ( D 2 ) T = d i a g { g ′ ( z ( 3 ) ) } (D^2)^{\mathrm{T}}=diag\{g^{'}(z^{(3)})\} (D2)T=diag{ g′(z(3))},对比公式 ( 34 ) (34) (34)和公式([37])可以很容易的发现这两个公式是等价的,具体的证明如下:令 g ′ ( z ( 3 ) ) g^{'}(z^{(3)}) g′(z(3))为 m × 1 m \times 1 m×1的列向量,即: p m × 1 = g ′ ( z ( 3 ) ) = ( p 1 ⋮ p m ) (38) \tag{38} p_{m \times 1} = g^{'}(z^{(3)})=\left (\begin{array}{c} p_1 \\ \vdots\\ p_m \end{array}\right) pm×1=g′(z(3))=⎝⎜⎛p1⋮pm⎠⎟⎞(38)可以容易推知 ( Θ ( 3 ) ) T δ ( 4 ) (\Theta^{(3)})^{\mathrm{T}} \delta^{(4)} (Θ(3))Tδ(4)也是一个 m × 1 m \times 1 m×1的列向量,令
h m × 1 = ( Θ ( 3 ) ) T δ ( 4 ) = ( h 1 ⋮ h m ) (39) \tag{39}h_{m \times 1} = (\Theta^{(3)})^{\mathrm{T}} \delta^{(4)}=\left (\begin{array}{c} h_1 \\ \vdots\\ h_m \end{array}\right) hm×1=(Θ(3))Tδ(4)=⎝⎜⎛h1⋮hm⎠⎟⎞(39)则公式 ( 37 ) (37) (37)可以重新整理为如下形式: h m × 1 ∗ p m × 1 = ( h 1 ⋅ p 1 ⋮ h m ⋅ p m ) (40) \tag{40} h_{m \times 1} * p_{m \times 1} = \left (\begin{array}{c} h_1 \cdot p_1 \\ \vdots\\ h_m \cdot p_m \end{array}\right) hm×1∗pm×1=⎝⎜⎛h1⋅p1⋮hm⋅pm⎠⎟⎞(40)
因为, p m × 1 = g ′ ( z ( 3 ) ) p_{m \times 1} = g^{'}(z^{(3)}) pm×1=g′(z(3)),则公式([37])中的矩阵 D 2 D^{2} D2可以写成:
D 2 = d i a g { p 1 , ⋅ ⋅ ⋅ , p m } = ( p 1 ⋅ ⋅ ⋅ 0 ⋮ ⋱ ⋮ 0 ⋅ ⋅ ⋅ p m ) (41) \tag{41} D^{2} = diag\{p_1, \cdot \cdot \cdot , p_m\}=\left (\begin{array}{ccc} p_1 &\cdot\cdot\cdot & 0 \\ \vdots & \ddots & \vdots\\ 0 &\cdot\cdot\cdot & p_m \end{array}\right) D2=diag{ p1,⋅⋅⋅,pm}=⎝⎜⎛p1⋮0⋅⋅⋅⋱⋅⋅⋅0⋮pm⎠⎟⎞(41)则公式 ( 34 ) (34) (34)可以重新整为如下形式: ( D 2 ) T ⋅ h m × 1 = ( p 1 ⋅ ⋅ ⋅ 0 ⋮ ⋱ ⋮ 0 ⋅ ⋅ ⋅ p m ) ⋅ ( h 1 ⋮ h m ) = ( h 1 ⋅ p 1 ⋮ h m ⋅ p m ) (42) \tag{42} (D^{2})^{\mathrm{T}} \cdot h_{m \times 1} = \left (\begin{array}{ccc} p_1 &\cdot\cdot\cdot & 0 \\ \vdots & \ddots & \vdots\\ 0 &\cdot\cdot\cdot & p_m \end{array}\right) \cdot \left (\begin{array}{c} h_1 \\ \vdots\\ h_m \end{array}\right)=\left (\begin{array}{c} h_1 \cdot p_1 \\ \vdots\\ h_m \cdot p_m \end{array}\right) (D2)T⋅hm×1=⎝⎜⎛p1⋮0⋅⋅⋅⋱⋅⋅⋅0⋮pm⎠⎟⎞⋅⎝⎜⎛h1⋮hm⎠⎟⎞=⎝⎜⎛h1⋅p1⋮hm⋅pm⎠⎟⎞(42)
根据公式([40])和([42])可知, δ ( 3 ) = e 2 \delta^{(3)}=e^{2} δ(3)=e2,证毕。
3)证明: δ ( 2 ) = e 1 \delta^{(2)}=e^{1} δ(2)=e1
证明 δ ( 2 ) = e 1 \delta^{(2)}=e^{1} δ(2)=e1过程跟证明 δ ( 3 ) = e 2 \delta^{(3)}=e^{2} δ(3)=e2方法一致,在此不过多赘述,证毕。
综上所述,我们可以发现讲义中的结论与本文中有如下等价关系: ∂ J ( Θ ) ∂ Θ ( l ) = δ ( l + 1 ) ( a ( l ) ) T ↔ ∂ F s ( θ ) ∂ W l = e l ( a l − 1 ) T (43) \tag{43} \frac{\partial J(\Theta)}{\partial \Theta^{(l)}} = \delta^{(l+1)} (a^{(l)})^{\mathrm{T}} \leftrightarrow \frac{\partial F_s(\theta)}{\partial W^{l}}=e^{l} (a^{l-1})^{\mathrm{T}} ∂Θ(l)∂J(Θ)=δ(l+1)(a(l))T↔∂Wl∂Fs(θ)=el(al−1)T(43)
其中, l = 1 , 2 , 3 l=1,2,3 l=1,2,3。对于权重矩阵 Θ ( l ) \Theta^{(l)} Θ(l)的第i行和第j列元素的偏导数即为:
∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i ( l + 1 ) (44) \tag{44} \frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=a_{j}^{(l)} \delta_{i}^{(l+1)} ∂Θij(l)∂J(Θ)=aj(l)δi(l+1)(44)
此公式就是讲义中最后给出的结果,这也就完美的验证了我之前的推导是正确的。

