pytorch实现YoloV3模型
yoloV3的学习笔记
以下内容是学习Bubbliiiing大佬,自己整理的笔记
大佬的CSDN链接 点击这里
YOLOv3
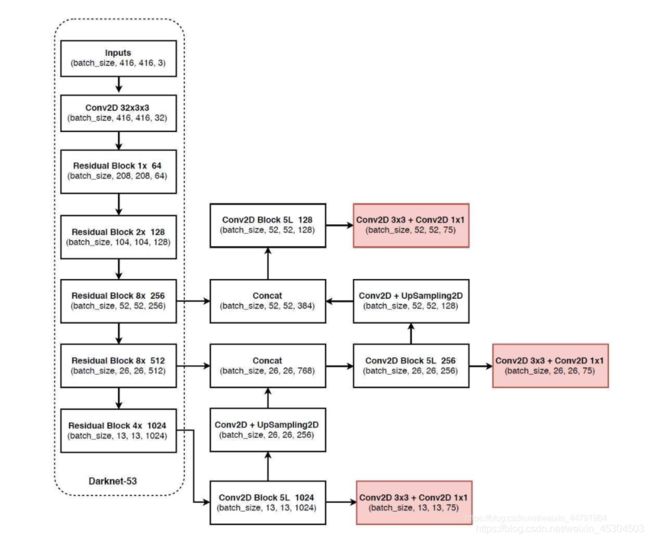
yolov3主要主要就是通过Darknet-53的主干网络进行特征的提取。首先是进行输入的数据的大小—>先是进行一次卷积的处理,增加通道数,
主干部分Darknet-53
主干网络是Darknet53,其重要特点是使用了残缺网络Residual。darknet53中的残差卷积就是进行一次3*3,步长为2的卷积,然后保存该卷积layer,再进行一次1 x 1的卷积和一次3x3的卷积
1.Darknet-53 主干部分
def darknet53(pretrained, **kwargs):
LoopList = [1, 2, 8, 8, 4] # 每一个残差网络块训练迭代的次数
model = DarkNet(LoopList)
if pretrained:
if isinstance(pretrained, str):
model.load_state_dict(torch.load(pretrained))
else:
raise Exception("darknet request a pretrained path. got[{}]".format(pretrained))
return model
class DarkNet(nn.Module): # 主干DarkNet53
def __init__(self, layers):
super(DarkNet, self).__init__()
self.inplanes = 32 # 通道数
# 416*416*3--->416*416*32 扩充通道数,即使扩充其中的特征图
"""1.卷积"""
self.conv1 = nn.Conv2d(3, self.inplanes, kernel_size=3, stride=1, padding=1, bias=False)
# 输入图像的深度-->3(一开始的RGB) 输出图像的深度-->后来变成了32
# kernel_size卷积核大小3*3 stride 步长1 padding 卷积是否造成尺寸丢失,1为不丢失
"""2.标准化"""
self.bn1 = nn.BatchNorm2d(self.inplanes)
# 对通道数进行标准化,还可以加一个参数表示进行百分之多少的标志化
"""3.激活函数"""
self.relu1 = nn.LeakyReLU(0.1)
# torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)
# negative_slope:控制负斜率的角度,默认等于0.01
# inplace-选择是否进行覆盖运算
# 1.能解决深度神经网络(层数非常多)的"梯度消失"问题,浅层神经网络(三五层那种)才用sigmoid 作为激活函数。
# 2.它能加快收敛速度。
"""Residual Block的不断堆叠"""
# 这些残差块的堆叠是为了进行特征的提取
# 416*416*32--->208*208*64
self.layerFirst = self._make_layer([32, 64], layers[0])
# 输入的通道数,输出的通道数,进行多少次类似的操作,即使传入进来的数组
# 208*208*64--->104*104*128
self.layerSecond = self._make_layer([64, 128], layers[1])
# 104*104*128--->52*52*256
self.layerThird = self._make_layer([128, 256], layers[2])
# 52*52*256--->26*26*512
self.layerFouth = self._make_layer([256, 512], layers[3])
# 26*26*512--->13*13*1024
self.layerFifth = self._make_layer([512, 1024], layers[4])
self.layers_out_filters = [64, 128, 256, 512, 1024]
for m in self.modules(): # 权值的初始化
if isinstance(m, nn.Conv2d):
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
def _make_layer(self, planes, blocks):
# 在每一个layer里面,首先利用一个步长为2的3*3的卷积进行下采样
# 然后再进行残差结构的堆叠
layers = []
layers.append(("ds_conv", nn.Conv2d(self.inplanes, planes[1], kernel_size=3, stride=2, padding=1, bias=False)))
layers.append(("ds_bn", nn.BatchNorm2d(planes[1]))) # 类似上面的卷积部分,提取特征
layers.append(("ds_relu", nn.LeakyReLU(0.1)))
# 加入残差
self.inplanes = planes[1]
for i in range(0, blocks):
layers.append(("residual_{}".format(i), BasicBlock(self.inplanes, planes)))
return nn.Sequential(OrderedDict(layers))
# 这是一个有顺序的容器,将特定神经网络模块按照在传入构造器的顺序依次被添加到计算图中执行
def forward(self,x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu1(x)
x = self.layerFirst(x)
x = self.layerSecond(x)
outThird = self.layerThird(x)
outForth = self.layerFouth(outThird)
outFifth = self.layerFifth(outForth)
return outThird, outForth, outFifth
2.残差块(基本组成)
class BasicBlock(nn.Module): # 主体的残差网络
def __init__(self, inplanes, planes):
super(BasicBlock, self).__init__()
# 两次的卷积操作
# 先是利用一个1*1的卷积下降通道数。进行一次整理浓缩。
self.conv1 = nn.Conv2d(inplanes, planes[0], kernel_size=1, stride=1, padding=0, bias=False)
self.bn1 = nn.BatchNorm2d(planes[0])
self.relu1 = nn.LeakyReLU(0.1)
# 然后利用一个3*3卷积提取特征并且提取特征并且上升通道数。将浓缩的部分扩大,使其变成了更加具有特征的东西。
self.conv2 = nn.Conv2d(planes[0], planes[1], kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes[1])
self.relu2 = nn.LeakyReLU(0.1)
def forward(self, x):
residual = x # 残差边
out = self.conv1(x)
out = self.bn1(out)
out = self.relu1(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu2(out)
out += residual
return out
特征提取部分(右边)
1.右边部分的红色部分
进行特征的提取以及预测
"""make_last_layers里面一共有七个卷积,前五个用于特征提取。后面两个用于获得yolo网络的预测结果"""
# 就是红色的框框以及其上层
def make_last_layers(filters_list, in_filters, out_filter):
m = nn.ModuleList([
# 特征提取
conv2d(in_filters, filters_list[0], 1), # 1*1卷积 压缩通道数
conv2d(filters_list[0], filters_list[1], 3), # 3*3卷积提取特征
conv2d(filters_list[1], filters_list[0], 1), # 更加高效,更少参数
conv2d(filters_list[0], filters_list[1], 3),
conv2d(filters_list[1], filters_list[0], 1),
# 用于yolo的预测
conv2d(filters_list[0], filters_list[1], 3),
nn.Conv2d(filters_list[1], out_filter, kernel_size=1, stride=1, padding=0, bias=True)
])
return m
2.concat 堆叠过程
网络之间紧密的相连,形成特征金字塔,使得特征变得更加明显。
class YoloBody(nn.Module):
def __init__(self, config):
super(YoloBody, self).__init__()
self.config = config
"""生成darknet53的主干模型"""
# 获取三个有效特征层,shape分别是
# 53*52*256
# 26*26*512
# 13*13*1024
# 用于堆叠
self.backbone = darknet53(None) # 获取darknet53的结构
# out_filters : [64,128,256,512,1024]
out_filters = self.backbone.layers_out_filters
# 计算yolo_head的输入通道数,对于voc数据集而言, 75 = 3*25 = 3*(20+1+4) 20个类
# final_out_filter_zero = final_out_filter_one = final_out_filters = 75
# 75 = 3*25 = 3*(20+1+4) 20个类
final_out_filter_zero = len(config["yolo"]["anchors"][0]) * (5 + config["yolo"]["classes"])
# len(config["yolo"]["anchors"][0]) 3个先验框 5=(1+4) config["yolo"]["classes"] =20 个类
self.last_layer_zero = make_last_layers([512, 1024], out_filters[-1], final_out_filter_zero)
# 七次卷积的操作
"""进行的第一次卷积+上采样的过程,为后面Concat堆叠成特征金字塔"""
final_out_filter_one = len(config["yolo"]["anchors"][1]) * (5 + config["yolo"]["classes"])
self.last_layer_one_conv = conv2d(512, 256, 1) # 1*1的卷积调整通道数
self.last_layer_one_upsample = nn.Upsample(scale_factor=2, mode='nearest') # 上采样
self.last_layer_one = make_last_layers([256, 512], out_filters[-2]+256, final_out_filter_one) # 得到特征.与其他堆叠
"""进行的第二次卷积+上采样的过程,为后面Concat堆叠成特征金字塔"""
final_out_filter_two = len(config["yolo"]["anchors"][2]) * (5 + config["yolo"]["classes"])
self.last_layer_two_conv = conv2d(256, 128, 1) # 1*1的卷积调整变成128的通道数
self.last_layer_two_upsample = nn.Upsample(scale_factor=2, mode='nearest')
self.last_layer_two = make_last_layers([128, 256], out_filters[-3] + 128, final_out_filter_two) # 得到特征.与其他堆叠
def forward(self, x): # 向前传递
def _branch(last_layer, layer_in): # 将5次卷积的结果保存,因为make_last_layers是七次的,把5次和2次分开。
for i, e in enumerate(last_layer):
layer_in = e(layer_in)
if i == 4:
out_branch = layer_in
return layer_in, out_branch
# 获取三个有效的特征层,他们的shape分别是:
# 52*52*256 26*26*512 13*13*1024
x_two, x_one, x_zero = self.backbone(x) # 将这个输入的x通过darknet提取三个特征层,用作堆叠。
"""第一个特征层 out_zero = (batch_size,255,13,13)"""
# 13,13,1024 -> 13,13,512 -> 13,13,1024 -> 13,13,512 -> 13,13,1024 -> 13,13,512
out_zero, out_zero_branch = _branch(self.last_layer_zero, x_zero)
# 13,13,512 -> 13,13,256 -> 26,26,256 # 卷积
x_one_in = self.last_layer_one_conv(out_zero_branch)
x_one_in = self.last_layer_one_upsample(x_one_in)
# 26,26,256 + 26,26,512 -> 26,26,768 # 堆叠过程
x_one_in = torch.cat([x_one_in, x_one], 1)
"""第二个特征层 out_one = (batch_size,255,26,26)"""
# 26,26,768 -> 26,26,256 -> 26,26,512 -> 26,26,256 -> 26,26,512 -> 26,26,256
out_one, out_one_branch = _branch(self.last_layer_one, x_one_in)
# 26,26,256 -> 26,26,128 -> 52,52,128 # 卷积
x_two_in = self.last_layer_two_conv(out_one_branch)
x_two_in = self.last_layer_two_upsample(x_two_in)
# 52,52,128 + 52,525,256 --->52,52,384 # 堆叠过程
x_two_in = torch.cat([x_two_in, x_two], 1)
"""第三个特征层 out_two = (batch_size ,255,52,52)"""
# 52,52,384 -> 52,52,128 -> 52,52,256 -> 52,52,128 -> 52,52,256 -> 52,52,128
out_two, _ = _branch(self.last_layer_two, x_two_in) # 最后一次只是需要其中的第一个预测这一部分
return out_zero, out_one, out_two
其他知识点
1.关于池化层(下采样层)
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合。简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像。
下采样层也叫池化层,其具体操作与卷积层的操作基本相同,只不过下采样的卷积核为只取对应位置的最大值、平均值等(最大池化、平均池化),即矩阵之间的运算规律不一样,并且不经过反向传播的修改。
主要是两个作用:
1.invariance(不变性),这种不变性包括translation(平移),rotation(旋转),scale(尺度)
2.保留主要的特征同时减少参数(降维,效果类似PCA)和计算量,防止过拟合,提高模型泛化能力
特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用
(1) translation invariance:(特征不变性)
这里举一个直观的例子(数字识别),假设有一个16x16的图片,里面有个数字1,我们需要识别出来,这个数字1可能写的偏左一点(图1),这个数字1可能偏右一点(图2),图1到图2相当于向左向右平移了一个单位,但是图1和图2经过max pooling之后它们都变成了相同的8x8特征矩阵,主要的特征我们捕获到了,同时又将问题的规模从16x16降到了8x8,而且具有平移不变性的特点。图中的a(或b)表示,在原始图片中的这些a(或b)位置,最终都会映射到相同的位置。
(2) rotation invariance:(特征降维)
下图表示汉字“一”的识别,第一张相对于x轴有倾斜角,第二张是平行于x轴,两张图片相当于做了旋转,经过多次max pooling后具有相同的特征
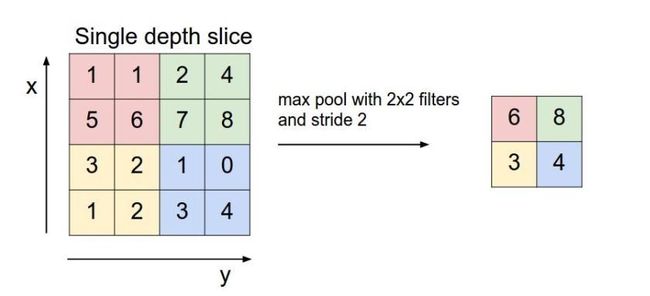
池化层用的方法有Max pooling 和 average pooling,而实际用的较多的是Max pooling。
这里就说一下Max pooling,其实思想非常简单。

对于每个2x2的窗口选出最大的数作为输出矩阵的相应元素的值,比如输入矩阵第一个2*2窗口中最大的数是6,那么输出矩阵的第一个元素就是6,如此类推。
2.关于通道数
在计算机视觉处理中,一般图片数据除了是单通道的灰度图片外,就是RGB通道的彩色图片了,对RGB图片进行卷积操作后,根据过滤器的数量就可以产生更多的通道。事实上,多数情况还是叫后面的卷积层中的通道为,特征图。但实际上在张量表示下,特征图和前面提到的通道差不多,有时候后面的也都叫通道了。一种卷积核得到一个通道,所以特征图个数=输出通道数=卷积核个数。
这样看来,图片中的通道就是某种意义上的特征图。一个通道是对某个特征的检测,通道中某一处数值的强弱就是对当前特征强弱的反应。
如一个蓝色通道中,如果是256级的话,那么一个像素如果是255的话那么就表示蓝色度很大。从这个角度来看灰度图片的话,就会发现其实灰度图片就是一个白色过滤器生成的特征图。于是卷积网络中的特征图,也能够很直接地理解为通道了。
之后通过对一定范围的特征图进行卷积,可以将多个特征组合出来的模式抽取成一个特征,获得下一个特征图。
再继续,对特征图进行卷积,特征之间继续组合,获得更复杂的特征图。
又因为池化层的存在,会不断提取一定范围内最强烈的特征,并且缩小张量的大小,使得大范围内的特征组合也能够捕捉到。
3.关于1x1卷积的作用
通过特征角度来看卷积网络的话,那么1x1卷积也就很好理解了。即使1x1卷积前后的张量大小完全不变,比如说16x16x64 -> 16x16x64这样的卷积,看上去好像是没有变化。但实际上,可能通过特征之间的互动,已经由之前的64个特征图组成了新的64个特征图。有时候我理解一个这样的1x1卷积操作,就会把它当成是一次对之前特征的整理。
这样子不停卷积下去,直到最后一层,剩下一个一维向量时,每个标量代表着一个通道,捕捉到的特征又是什么呢。如果是物体分类任务的话,就正是我们需要输出判别的一个个物体类别。
比如说第一个数是代表猫特征,第二个数代表狗特征,第三个代表人… 这个时候去从里面选数值最大那个当做分类的种类就好了。到这里可能仔细的人会注意,最后几层不是没卷积操作吗,而是全连接网络。
一个概念上需要澄清的是,虽然说1x1卷积,而且也从融合特征角度,给了它特殊的理解。但如果再仔细看看的话,就会发现实际上1x1卷积就是全连接网络。所以我们可以把最后的1x1网络当成某种程度上的1x1卷积。
上面的网络最后几层,将张量展平然后输入全连接网络。因为剩下的特征图中都保留了很重要的信息,为了利用所有的信息,并且让它们获得足够的交互,所以直接输入全连接网络,获得最后的特征向量。
4.关于非极大值抑制(Non-Maximum Suppression,NMS)
顾名思义就是抑制不是极大值的元素,可以理解为局部最大搜索。这个局部代表的是一个邻域,邻域有两个参数可变,一是邻域的维数,二是邻域的大小
目标是去除冗余的先验框,保留其中最好的一个
![]()
NMS原理
对于Bounding Box的列表B及其对应的置信度S,采用下面的计算方式。选择具有最大score的检测框M,将其从B集合中移除并加入到最终的检测结果D中。通常将B中剩余检测框中与M的IoU大于阈值Nt的框从B中移除。重复这个过程,直到B为空。
重叠率(重叠区域面积比例IOU)阈值
常用的阈值是 0.3 ~ 0.5。其中用到排序,可以按照右下角的坐标排序或者面积排序,也可以是通过SVM等分类器得到的得分或概率,R-CNN中就是按得分进行的排序。

就像上面的图片一样,定位一个车辆,最后算法就找出了一堆的先验框,我们需要判别哪些先验框是没用的。非极大值抑制的方法是:先假设有6个矩形框,根据分类器的类别分类概率做排序,假设从小到大属于车辆的概率 分别为A、B、C、D、E、F。
(1)从最大概率矩形框F开始,分别判断A~E与F的重叠度IOU是否大于某个设定的阈值;
(2)假设B、D与F的重叠度超过阈值,那么就扔掉B、D;并标记第一个矩形框F,是我们保留下来的。
(3)从剩下的矩形框A、C、E中,选择概率最大的E,然后判断E与A、C的重叠度,重叠度大于一定的阈值,那么就扔掉;并标记E是我们保留下来的第二个矩形框。
遍历其余的框,如果和当前最高分框的重叠面积(IOU)大于一定阈值,我们就将框删除。就这样一直重复,找到所有被保留下来的矩形框