现代数字信号处理课后作业【第七章】&IIR巴特沃兹&FIR数字滤波器设计

现代数字信号处理课后作业【第七章】

窗函数设计原理：
$设希望逼近的滤波器频率响应函数为H_d(e^{jw})$，$其单位脉冲响应是h_d(n)$。$$\begin{gathered} H_d(e^{jw})=\sum _{n=-\infty }^{\infty }{h}_d(n)e^{-jwn} \\ {h}_d(n)=\frac{1}{2\pi }{\int }_{-w_c}^{w_c}{H}_d(e^{jw})dw \end{gathered}$$$h_d(n)是无限时宽，且是非因果序列。$
$$\begin{gathered} 第一类线性相位FIR滤波器当序列长度N为奇数时，可实现：低通、高通、带通、带阻滤波器 \\ 当N为偶数时，可实现：低通、带通滤波器。 \end{gathered}$$
$为了构造第一类线性相位FIR滤波器，则需要将h_d(n)截取一段，并保证截取的一段关于n=\frac{N-1}{2}偶对称，即h(n)=h_d(n)w(n)，其中w(n)为窗函数。$
$设H_d(e^{jw})=H_{dg}(w)e^{-jw\alpha }，其中\alpha 为群延时，H_{dg}(w)为数字滤波器的幅度特性。$
$当\alpha =\frac{N-1}{2}，截取的一段h(n)关于n=\frac{N-1}{2}偶对称，保证所设计的滤波器具有线性相位。$

窗函数设计步骤：
$①：构造希望逼近的频率响应函数H_d(e^{jw})=H_{dg}(w)e^{-jw(N-1)/2}$
$②：确定滤波器频带边界条件，计算h_d(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{H}_d(e^{jw})e^{jwn}dw$
$③：加窗得到设计结果h(n)=h_d(n)w(n)$

7-1 要求设计一个线性相位数字滤波器（矩形窗）。$H_d(e^{jw})=\{\begin{array}{ll}{e}^{-jw\alpha }& w_1⩽|w|⩽w_2\\ 0& 其它\end{array}$

(1) N为奇数，求$h(n)$

 $\alpha =\frac{N-1}{2}$

 $h_d(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{H}_d(e^{jw})e^{jwn}dw$

$=\frac{1}{2\pi }[{\int }_{-w_2}^{-w_1}{e}^{-jw\alpha }\cdot e^{jwn}dw+{\int }_{w_1}^{w_2}{e}^{-jw\alpha }\cdot e^{jwn}dw]$

 $=\frac{sin[w_2(n-\alpha )]-sin[w_1(n-\alpha )]}{\pi (n-\alpha )}$

 $h(n)=h_d(n)R_N(n)$

 $=\frac{sin[w_2(n-\frac{N-1}{2})]-sin[w_1(n-\frac{N-1}{2})]}{\pi (n-\frac{N-1}{2})}\cdot R_N(n)$

 $=\frac{1}{\pi }\{w_{2}Sa[w_2(n-\frac{N-1}{2})]-w_{1}Sa[w_1(n-\frac{N-1}{2})]\}\cdot R_N(n)$

 $当N为奇数时：$

 $h(n)=\{\begin{array}{ll}\frac{w_2-w_1}{\pi }\cdot R_N(n)=\frac{w_2-w_1}{\pi }& n=\frac{N-1}{2}\\ & \\ \frac{sin[w_2(n-\frac{N-1}{2})]-sin[w_1(n-\frac{N-1}{2})]}{\pi (n-\frac{N-1}{2})}\cdot R_N(n)& n\ne \frac{N-1}{2}\end{array}$

(2) N为偶数，求$h(n)$

 $h(n)=\frac{sin[w_2(n-\frac{N-1}{2})]-sin[w_1(n-\frac{N-1}{2})]}{\pi (n-\frac{N-1}{2})}\cdot R_N(n)$

(3) 若用布莱克曼窗设计，求出以上两种形式的$h(n)$表达式

 $布莱克曼窗w_{Bl}(n)=[0.42-0.5cos(\frac{2\pi n}{N-1})+0.08cos(\frac{4\pi n}{N-1})]R_N(n)$

 $当N为奇数时：$

 $h(n)=\{\begin{array}{ll}\frac{w_2-w_1}{\pi }\cdot w_{Bl}(n)=\frac{w_2-w_1}{\pi }& n=\frac{N-1}{2}\\ \frac{1}{\pi }\{w_{2}Sa[w_2(n-\frac{N-1}{2})]-w_{1}Sa[w_1(n-\frac{N-1}{2})]\}\cdot w_{Bl}(n)& n\ne \frac{N-1}{2}\end{array}$

 $当N为偶数时：$

 $h(n)=\frac{sin[w_2(n-\frac{N-1}{2})]-sin[w_1(n-\frac{N-1}{2})]}{\pi (n-\frac{N-1}{2})}\cdot W_{Bl(n)}$

7-2 按$H_d(e^{jw})=\{\begin{array}{ll}0& w_1⩽|w|⩽w_2\\ e^{-jw\alpha }& 其它\end{array}$，设计一个带阻滤波器。

(1) N为奇数，求$h(n)$

 $\alpha =\frac{N-1}{2}$

 $h_d(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{H}_d(e^{jw})e^{jwn}dw$

$=\frac{1}{2\pi }[{\int }_{-\pi }^{-w_2}{e}^{-jw\alpha }{e}^{jwn}dw+{\int }_{-w_1}^{w_1}{e}^{-jw\alpha }{e}^{jwn}dw+{\int }_{w_2}^{\pi }{e}^{-jw\alpha }{e}^{jwn}dw]$

 $=\frac{sin[w_1(n-\alpha )]-sin[w_2(n-\alpha )]+sin[\pi (n-\alpha )]}{\pi (n-\alpha )}$

 $h(n)=h_d(n)R_N(n)$

 $当N为奇数时：$

 $h(n)=\{\begin{array}{ll}\frac{w_1-w_2+\pi }{\pi }\cdot R_N(n)=\frac{w_1-w_2+\pi }{\pi }& n=\frac{N-1}{2}\\ \frac{sin[w_1(n-\alpha )]-sin[w_2(n-\alpha )]+sin[\pi (n-\alpha )]}{\pi (n-\alpha )}\cdot R_N(n)& n\ne \frac{N-1}{2}\end{array}$

(2) N为偶数，求$h(n)$

 $h(n)=\frac{sin[w_1(n-\alpha )]-sin[w_2(n-\alpha )]+sin[\pi (n-\alpha )]}{\pi (n-\alpha )}\cdot R_N(n)$

(3) 若用布莱克曼窗设计，求出以上两种形式的$h(n)$表达式

 $布莱克曼窗w_{Bl}(n)=[0.42-0.5cos(\frac{2\pi n}{N-1})+0.08cos(\frac{4\pi n}{N-1})]R_N(n)$

 $当N为奇数时：$

 $h(n)=\{\begin{array}{ll}\frac{w_1-w_2+\pi }{\pi }\cdot w_{Bl}(n)=\frac{w_1-w_2+\pi }{\pi }注：w_{Bl}(\frac{N-1}{2})=1& n=\frac{N-1}{2}\\ \frac{sin[w_1(n-\alpha )]-sin[w_2(n-\alpha )]+sin[\pi (n-\alpha )]}{\pi (n-\alpha )}\cdot w_{Bl}(n)& n\ne \frac{N-1}{2}\end{array}$

 $当N为偶数时：$

 $h(n)=\frac{sin[w_1(n-\alpha )]-sin[w_2(n-\alpha )]+sin[\pi (n-\alpha )]}{\pi (n-\alpha )}\cdot w_{Bl}(n)$

7-5 用频率采样法设计一个线性相位低通滤波器，N=15时幅度采样为：$$H_{dg}(k)=\{\begin{array}{ll}1& k=0\\ 0.5& k=1,14\\ 0& k=2,3,...,13\end{array}$$

频率采样法设计FIR滤波器的基本思想：
$设希望逼近的滤波器的频响函数用H_d(e^{jw})表示，对H_d(e^{jw})在w=0到2\pi 之间等间隔采样N点，得到H_d(k):$$$H_d(k)=H_d(e^{jw}){|}_{w=\frac{2\pi k}{N}}k=0,1,2,...,N-1$$
$设H_d(e^{jw})=H_{dg}(w)e^{-jw\alpha }，其中\alpha =\frac{N-1}{2}为群延时，H_{dg}(w)为数字滤波器的幅度特性。$
$$H_d(k)=H_{dg}(k)e^{-j\frac{2\pi k\alpha }{N}}=H_{dg}(k)e^{-j\frac{N-1}{N}\pi k}$$
$再对H_d(k)进行N点IDFT，得到h(n):$$$h(n)=\frac{1}{N}\sum _{k=0}^{N-1}{H}_d(k)W_N^{-kn}n=0,1,2,...,N-1$$
$将h(n)作为所设计的FIR滤波器的单位脉冲响应，其系统函数H(z)为:$$$H(z)=\sum _{n=0}^{N-1}h(n)z^{-n}(该式适合FIR直接型网络结构)$$
$根据频率域采样理论，得到H(z)的内插表示形式：$ $$\begin{array}{rl}H(z)& =\frac{1}{N}\sum _{n=0}^{N-1}\sum _{k=0}^{N-1}{H}_d(k)W_N^{-kn}{z}^{-n}\\ & =\frac{1}{N}\sum _{k=0}^{N-1}{H}_d(k)\sum _{n=0}^{N-1}{W}_N^{-kn}{z}^{-n}\\ & =\frac{1}{N}\sum _{k=0}^{N-1}{H}_d(k)\frac{1-W_N^{-kN}{z}^{-N}}{1-W_N^{-k}{z}^{-1}}\\ & =\frac{1-z^{-N}}{N}\sum _{k=0}^{N-1}\frac{H_d(k)}{1-W_N^{-k}{z}^{-1}}(该式适合频率采样结构)\end{array}$$

(1) 求$h(n)、H(e^{jw})$的表达式

 $H_d(k)=H_{dg}(k)e^{-j\frac{N-1}{N}\pi k}=\{\begin{array}{ll}{e}^{-j\frac{14}{15}\pi k}& k=0\\ 0.5e^{-j\frac{14}{15}\pi k}& k=1,14\\ 0& k=2,3,...,13\end{array}$

 $h(n)=\frac{1}{N}\sum _{k=0}^{N-1}{H}_d(k)W_N^{-kn}=\frac{1}{15}(W_{15}^0+0.5W_{15}^{-n}{e}^{-j\frac{14}{15}\pi }+0.5W_{15}^{-14n}{e}^{-j\frac{14^2}{15}\pi })$

 $=\frac{1}{15}[1+0.5e^{\frac{j2\pi (n-7)}{15}}+0.5e^{\frac{-j2\pi (n-7)}{15}}]$

 $=\frac{1+cos[\frac{2\pi (n-7)}{15}]}{15}$

 $H(z)=\frac{1-z^{-N}}{N}\sum _{k=0}^{N-1}\frac{H_d(k)}{1-W_N^{-k}{z}^{-1}}$

 $H(z)=\frac{1-z^{-15}}{15}\sum _{k=0}^{14}\frac{H_d(k)}{1-W_{15}^{-k}{z}^{-1}}$

 $=\frac{1-z^{-15}}{15}(\frac{1}{1-z^{-1}}+\frac{0.5e^{-j\frac{14}{15}\pi }}{1-W_{15}^{-1}{z}^{-1}}+\frac{0.5e^{-j\frac{14^2}{15}\pi }}{1-W_{15}^{-14}{z}^{-1}})$

 $=\frac{1-z^{-15}}{15}(\frac{1}{1-z^{-1}}+\frac{0.5e^{-j\frac{14}{15}\pi }}{1-e^{j\frac{2\pi }{15}}{z}^{-1}}+\frac{0.5e^{j\frac{14}{15}\pi }}{1-e^{-j\frac{2\pi }{15}}{z}^{-1}})$

 $H(e^{jw})=H(z){|}_{z=e^{jw}}=\frac{1-e^{-j15w}}{15}(\frac{1}{1-e^{-jw}}+\frac{0.5e^{-j\frac{14}{15}\pi }}{1-e^{j\frac{2\pi }{15}}{e}^{-jw}}+\frac{0.5e^{j\frac{14}{15}\pi }}{1-e^{-j\frac{2\pi }{15}}{e}^{-jw}})$

(2) 用直接型及频率采样型两种结构实现这一滤波器，画出结构图

• 直接型：

 $H(z)=\sum _{n=0}^{N-1}h(n)z^{-n}=\sum _{n=0}^{14}\frac{1+cos[\frac{2\pi (n-7)}{15}]}{15}{z}^{-n}$

• 直接型结构图：

• 频率采样型：

 $H(z)=\frac{1-z^{-N}}{N}\sum _{k=0}^{N-1}\frac{H_d(k)}{1-W_N^{-k}{z}^{-1}}$

 $H(z)=\frac{1-z^{-15}}{15}\sum _{k=0}^{14}\frac{H_d(k)}{1-W_{15}^{-k}{z}^{-1}}$

 $=\frac{1-z^{-15}}{15}(\frac{1}{1-z^{-1}}+\frac{0.5e^{-j\frac{14}{15}\pi }}{1-W_{15}^{-1}{z}^{-1}}+\frac{0.5e^{-j\frac{14^2}{15}\pi }}{1-W_{15}^{-14}{z}^{-1}})$

 $=\frac{1-z^{-15}}{15}(\frac{1}{1-z^{-1}}+\frac{0.5e^{-j\frac{14}{15}\pi }}{1-e^{j\frac{2\pi }{15}}{z}^{-1}}+\frac{0.5e^{j\frac{14}{15}\pi }}{1-e^{-j\frac{2\pi }{15}}{z}^{-1}})$

• 频率采样型结构图：

7-8 用窗函数法设计FIR线性相位数字低通滤波器LPF，已知：$w_c=0.5\pi ，N=21$，求$h(n),H(e^{jw})$并画出图形。

 $H_d(e^{jw})=\{\begin{array}{ll}{e}^{-jw\alpha }& |w|⩽w_c\\ 0& 其它\end{array}$

 $\alpha =\frac{N-1}{2}$

 $h_d(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{H}_d(e^{jw})e^{jwn}dw$

 $=\frac{1}{2\pi }{\int }_{-w_c}^{w_c}{e}^{jw(n-\alpha )}dw$

 $=\frac{sin[w_c(n-\alpha )]}{\pi (n-\alpha )}$

 $h(n)=h_d(n)R_N(n)$

 $=\frac{sin[w_c(n-\frac{N-1}{2})]}{\pi (n-\frac{N-1}{2})}\cdot R_N(n)$

 $=\frac{sin[0.5\pi (n-10)]}{\pi (n-10)}\cdot R_{21}(n)$

 $H(e^{jw})=\sum _{n=0}^{N-1}h(n)e^{-jwn}=\sum _{n=0}^{20}\frac{sin[0.5\pi (n-10)]}{\pi (n-10)}{e}^{-jwn}=\sum _{n=0}^{20}0.5sinc[0.5(n-10)]e^{-jwn}$

• 幅频特性图：

• Matlab代码块：

B=zeros(1,21);
A=1;
for n=1:21
   B(n)=0.5*sinc(0.5*((n-1)-10));    
end

figure;
subplot(2,1,1);
stem(0:20,B,'r.');
xlabel('n');ylabel('h(n)');grid on;title('h(n)');
[H,w]=freqz(B,A,'whole');
subplot(2,1,2);
plot(w/pi,abs(H));
xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');grid on;title('幅频特性');

实验题：50Hz,1KHz两路1：1混合信号，设计滤波器

(1) IIR滤波器，低通获得50Hz，1KHz衰减>100倍

题意解读：
$衰减倍数与dB的关系：20lg(\frac{V_o}{V_i})$
$所以此题衰减大于100倍，即20lg(\frac{1}{100})=-40dB$
$设输入信号：s(t)=sin(2\pi f_{1}t)+sin(2\pi f_{2}t)f_1=50Hz，f_2=1000Hz，F_s=4000Hz$

$IIR模拟巴特沃兹低通滤波器:通带截止频率200Hz，阻带截止频率1000Hz，通带波纹最大衰减为1dB阻带衰减为40dB$

• Matlab代码块：原始信号及FFT谱分析

clc;
clear;
close all;

Fs=4000; % 采样频率4000Hz  
t=0:1/Fs:1;  
s50=sin(2*pi*50*t); % 产生50Hz正弦波  
s1000=sin(2*pi*1000*t); % 产生1000Hz正弦波  
s=s50+s1000; % 混合信号：信号叠加
  
figure; % 画图  
subplot(2,1,1);plot(s);grid on;  
axis([0 1000 -2 2]);
title('原始信号50Hz和1000Hz正弦波混合');  


% -----------------FFT分析信号频谱----------------------  
len = 1024;    
y=fft(s,len);  % 对原始输入信号做len点FFT变换  
f=Fs*(0:len/2 - 1)/len;  
  
subplot(2,1,2);plot(f,abs(y(1:len/2)));grid on;  
title('原始信号频谱')  
xlabel('Hz');ylabel('幅值');  

• 运行结果：

• IIR模拟巴特沃兹低通滤波器设计：

% ------------------------IIR模拟低通滤波器设计---------------------------  
Fp=200; % 通带截止频率200Hz  
Fc=1000; % 阻带截止频率1000Hz  
Rp=1; % 通带波纹最大衰减为1dB  
Rs=40; % 阻带衰减为40dB    20lg(1/100)=40dB   
%-----------------------计算最小滤波器阶数-----------------------------  
na=sqrt(10^(0.1*Rp)-1);  
ea=sqrt(10^(0.1*Rs)-1);  
N=ceil(log10(ea/na)/log10(Fc/Fp));   %巴特沃兹阶数  
%----------------------巴特沃兹低通滤波器------------------------------  
Wn=Fp*2/Fs;  
[Bb Ba]=butter(N,Wn,'low'); % 调用MATLAB butter函数快速设计滤波器  
[BH,BW]=freqz(Bb,Ba); % 绘制频率响应曲线

figure;
A1 = BW*Fs/(2*pi);
plot(A1,abs(BH));
grid on;xlabel('频率／Hz'); ylabel('频率响应幅度'); 
title('巴特沃兹低通滤波器');

• 运行结果：

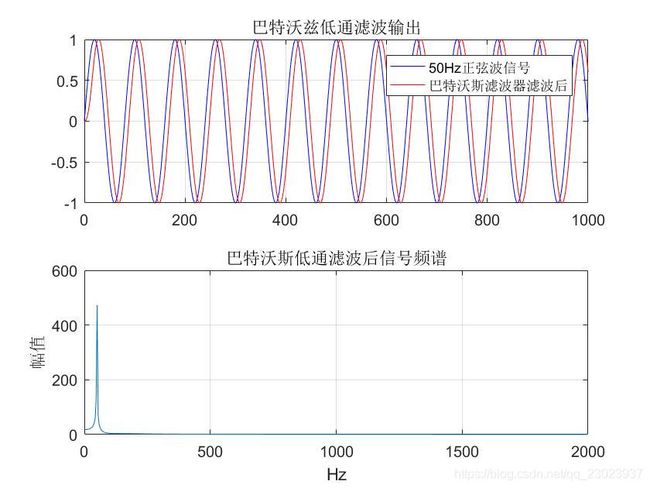
• 对原始信号进行低通滤波输出并分析频谱：

Bf=filter(Bb,Ba,s); % 进行低通滤波  
By=fft(Bf,len);  % 对滤波输出信号做len点FFT变换  

figure; % 画图  
subplot(2,1,1);plot(t*Fs,s50,'blue',t*Fs,Bf,'red');grid on;  
axis([0 1000 -1 1]);title('巴特沃兹低通滤波输出');
legend('50Hz正弦波信号','巴特沃斯滤波器滤波后');  
subplot(2,1,2);plot(f,abs(By(1:len/2)));grid on;  
title('巴特沃斯低通滤波后信号频谱');  
xlabel('Hz');ylabel('幅值');  

• 运行结果：

(2）FIR滤波器，高通获得1kHz，50Hz衰减>100倍

$FIR数字高通滤波器，由于阻带衰减大于40dB，因此选择汉宁窗$
$通带截止频率w_p=2\pi f_2/F_s$
$阻带截止频率w_s=2\pi f_1/F_s，由于该处w_s<\frac{\pi }{4}，故选择w_s=\frac{\pi }{4}$
$过渡带B=w_p-w_s$

• FIR数字高通滤波器设计：(汉宁窗)

%-----------------------确定相应的FIR数字滤波器指标-------------------------
wp=2*pi*1000/Fs;  %通带截止频率
% ws=2*pi*50/Fs;
ws=pi/4;      %阻带截止频率
Bt=wp-ws;     %过渡带带宽
N0=ceil(6.2*pi/Bt);  %汉宁窗窗长
N=N0+mod(N0+1,2);    %由于是高通滤波器，所以窗长N必须为奇数
wc=(wp+ws)/(2*pi);   %计算理想高通滤波器通带截止频率（关于pi归一化）
%----------------------FIR数字高通滤波器(汉宁窗)-------------------------
hn=fir1(N-1,wc,'high',hanning(N));  
[BH,BW]=freqz(hn,1); % 绘制频率响应曲线  

figure;
A1 = BW*Fs/(2*pi);
plot(A1,abs(BH));
grid on;xlabel('频率／Hz'); ylabel('频率响应幅度'); title('采用汉宁窗设置高通FIR数字滤波器');

• 运行结果：

• 对原始信号进行低通滤波输出并分析频谱：

Bf=filter(hn,1,s); % 进行高通滤波  
By=fft(Bf,len);  % 对高通滤波输出信号做len点FFT变换

figure; % 画图  
subplot(3,1,1);plot(t*Fs,s1000,'blue');grid on;  
axis([0 400 -1 1]);
title('原1000Hz正弦信号');
subplot(3,1,2);plot(t*Fs,Bf,'red');grid on;
axis([0 400 -1 1]);
title('FIR数字高通滤波后');
subplot(3,1,3);plot(f,abs(By(1:len/2)));grid;  
title('高通FIR数字滤波器滤波后信号频谱');  
xlabel('Hz');ylabel('幅值'); 

• 运行结果：