现代数字信号处理课后作业【完结篇】

---

感谢大家的陪伴，学无止境。

---

1、设各态历经平稳随机信号的观测值$x(n)=${1，-1，2，-2；n=0~3}；试用周期法和相关法求其功率谱估计值$P_N(w)$，验证其一致性。

周期图法：
①先求信号频谱函数$X_N(e^{jw})=\sum _{n=0}^{N-1}x(n)e^{-jwn}$
②再求功率谱密度$P_N(w)=\frac{1}{N}|X_N(e^{jw}){|}^2$

自相关法：
①首先在时域求序列自相关函数$r_N(m)=\frac{1}{N}{x}_N(m)\ast x_N^{\ast }(-m)=\frac{1}{N}\sum _{n=0}^{N-1}{x}_N(n)x_N(n-m)$
②再求其傅里叶变换得到功率谱密度$P_N(w)=\sum _{m=1-N}^{N-1}{r}_N(m)e^{-jwn}$

周期图估计法：

$x_4(n)=\{1,-1,2,-2\}N=4$

$X_4(e^{jw})=\sum _{n=0}^{3}x(n)e^{-jwn}=1-e^{-jw}+2e^{-j2w}-2e^{-j3w}$

$=(1-cosw+2cos2w-2cos3w)+j(sinw-2sin2w+2sin3w)$

$P_4(w)=\frac{1}{4}[(1-cosw+2cos2w-2cos3w{)}^2+(sinw-2sin2w+2sin3w{)}^2]$

$通过积化和差：cos\alpha cos\beta +sin\alpha sin\beta =cos(\alpha -\beta )$

$最后可化简得：P_4(w)=\frac{1}{4}(-4cos3w+8cos2w-14cosw+10)$

自相关估计法

$由于x_4(n)为实序列，所以x^{\ast }(-n)=x(-n)$

$r_4(m)=x(m)\ast x(-m)=\frac{1}{4}\sum _{n=0}^3{x}_4(n)x_4(n-m)$

$r_4(m)=\frac{1}{4}\{-2,4,-7,10,-7,4,-2\}m=-3,-2,...,2,3$

$P_4(w)=\sum _{m=-3}^3{r}_4(m)e^{-jwm}$

$=\frac{1}{4}\cdot (-2e^{j3w}+4e^{j2w}-7e^{jw}+10-7e^{-jw}+4e^{-j2w}-2e^{-j3w})$

$=\frac{1}{4}[-2(e^{j3w}+e^{-j3w})+4(e^{j2w}+e^{-j2w})-7(e^{jw}+e^{-jw})+10]$

$=\frac{1}{4}(-4cos3w+8cos2w-14cosw+10)$

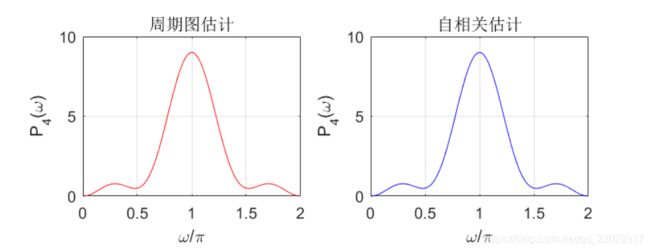
Matlab绘图验证二者功率谱图像：

Matlab代码：

clc;
clear;
close all;
 
xn=[1,-1,2,-2];
N=length(xn);
rm=xcorr(xn); %计算自相关

figure('name','功率谱估计');
B=xn;
A=1;
[H1,w]=freqz(B,A,'whole');
subplot(2,2,1);
plot(w/pi,1/N*(abs(H1)).^2,'r');
xlabel('\omega/\pi');ylabel('P_4(\omega)');grid on;title('周期图估计');

B=rm/N;
A=1;
[H2,w]=freqz(B,A,'whole');
subplot(2,2,2);
plot(w/pi,abs(H2),'b');
xlabel('\omega/\pi');ylabel('P_4(\omega)');grid on;title('自相关估计');

P1=0.25*((1-cos(w)+2*cos(2*w)-2*cos(3*w)).^2+(-sin(w)+2*sin(2*w)-2*sin(3*w)).^2); %周期图估计结果
P2=0.25*(-4*cos(3*w)+8*cos(2*w)-14*cos(w)+10); %自相关估计结果

subplot(2,2,3);plot(w/pi,P1,'r');
xlabel('\omega/\pi');ylabel('P_4(\omega)');grid on;title('周期图估计');
subplot(2,2,4);plot(w/pi,P2,'b');
xlabel('\omega/\pi');ylabel('P_4(\omega)');grid on;title('自相关估计');