图解算法:递归回溯分治
目录
- 第一章 递归算法介绍
- 第二章 递归算法应用
-
- 2.1、求阶乘
- 2.2、求年龄
- 第三章 回溯算法介绍
- 第四章 回溯算法应用
-
- 4.1、走迷宫
- 4.2、八皇后
- 第五章 分治算法介绍
- 第六章 分治算法应用
-
- 6.1、汉诺塔
- 6.2、棋盘覆盖
项目地址:https://gitee.com/caochenlei/algorithms
第一章 递归算法介绍
递归算法(recursion algorithm)又称递归法,简单的来说,就是函数自己调用自己。绝大多数编程语言中都支持函数的自调用,在这些语言中函数是可以通过调用自身来进行递归的。计算理论可以证明递归的作用可以完全取代循环,因此在很多函数编程语言中习惯用递归来实现循环。
那么“递归”和“循环”如何形象的描述呢?
- 递归: 你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开它。若干次之后,你打开面前的门后,发现只有一间屋子,没有门了。然后,你开始原路返回,最终还是可以返回到原点。一般来说,递归需要有边界条件(这里指最后那间屋子)、递归前进段(这里指去的过程)和递归返回段(这里指返回的过程)。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
- 循环: 在你打开门之前,手里就已经拿了若干把钥匙,每一把钥匙可以打开一道门,当你一扇一扇门打开过去,最终手里的钥匙就会全部用掉,最终成功的从房间里出去,也就是一去不复返,这里不考虑死循环。
第二章 递归算法应用
2.1、求阶乘
计算阶乘的程序在数学上定义为:
而使用代码来实现却也是很简单:
public class Factorial {
public static void main(String[] args) {
System.out.println("5的阶乘:" + fact(5));
}
//求阶乘
public static int fact(int n) {
if (n == 0) {
return 1;
}
return n * fact(n - 1);
}
}
5的阶乘:120
2.2、求年龄
有5个人坐在一起,问第5个人多少岁,他说比第4个人大2岁。问第4个人多少岁,他说比第3个人大2岁。问第3个人多少岁,他说比第2个人大2岁。问第2个人多少岁,他说比第1个人大2岁。最后问第1个人,他说是10岁。请问第5个人多大?
计算年龄的程序在数学上定义为:
而使用代码来实现却也是很简单:
public class Age {
public static void main(String[] args) {
System.out.println(age(5));
}
//求年龄
public static int age(int n) {
if (n == 1) {
return 10;
}
return age(n - 1) + 2;
}
}
18
第三章 回溯算法介绍
回溯算法(backtracking algorithm)又称试探法,实际上是一个类似枚举搜索尝试的过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
我们实际上可以这么想,如果现在有一个迷宫,有一个入口,有一个出口,也只有一条路可以走出去,如果这个迷宫并没有规律,而是随机生成的,这个时候,一般来说,我们就会每一条路不停的尝试,发现这条路走不通,就会回退到某一点,然后继续尝试,直到最终走出去,其实这就是回溯的一种应用。
第四章 回溯算法应用
4.1、走迷宫
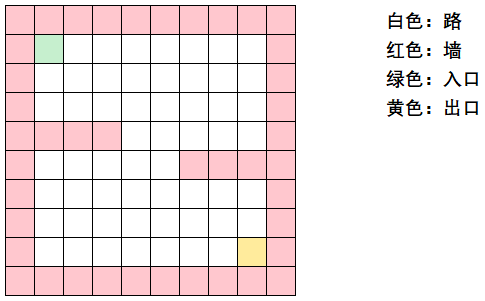
首先我们需要创建一张地图,这里使用二维数组来代替地图中的数据,没有走过的路为0,红色墙的挡板为1,可以走的通路为2,走不通的路为3。上图的绿色方块和黄色方块并没有特殊意义,只是为了告诉大家迷宫入口和出口在哪里。当然了,地图可以设计的很复杂,里边的挡板也可以设计的很复杂,但是为了很好的让大家接受大家暂且和我保持一致,我们就使用上边那张地图。生成地图的代码如下:
public class Maze {
public static void main(String[] args) {
//1.创建地图
int[][] map = createMap(10, 10);
//2.打印地图
System.out.println("初始化地图:");
displayMap(map);
//3.走迷宫
//4.打印地图
}
//创建地图
public static int[][] createMap(int rows, int cols) {
//...
}
//打印地图
//走迷宫
}
//创建地图
public static int[][] createMap(int rows, int cols) {
//创建地图
int[][] map = new int[rows][cols];
//建立围墙
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
//绘制第一行和最后一行的墙
if (i == 0 || i == rows - 1) {
map[i][j] = 1;
}
//绘制第一列和最后一列的墙
if (j == 0 || j == cols - 1) {
map[i][j] = 1;
}
}
}
//添加挡板
map[4][0] = 1;
map[4][1] = 1;
map[4][2] = 1;
map[4][3] = 1;
map[5][6] = 1;
map[5][7] = 1;
map[5][8] = 1;
map[5][9] = 1;
//返回地图
return map;
}
生成完地图后,我们需要打印一下地图的数据来查看一下地图是否生成正确。打印地图的代码如下:
//打印地图
public static void displayMap(int[][] map) {
//地图行数
int rows = map.length;
//地图列数
int cols = map[0].length;
//打印地图
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 1 1 1 0 0 0 0 0 1
1 0 0 0 0 0 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1
看着上边的地图,从绿色的入口出发,我们只能进行上下左右四个方向的走,因此,我们并不能确定先走哪一个方向比较好,并且上下左右有很多组合:
上 下 左 右
上 下 右 左
上 左 下 右
上 左 右 下
上 右 下 左
上 右 左 下
下 上 左 右
下 上 右 左
下 左 上 右
下 左 右 上
下 右 上 左
下 右 左 上
左 上 下 右
左 上 右 下
左 下 上 右
左 下 右 上
左 右 上 下
左 右 下 上
右 上 下 左
右 上 左 下
右 下 上 左
右 下 左 上
右 左 上 下
右 左 下 上
我们可以先观察地图,发现往右走和往下走比较好,所以,我们先指定一个走迷宫的策略:下->右->上->左,先往下走,往下走不通,往右走,往右走不通,往上走,往上走不通,往左走,我们就把这个点标记为3,直到我们走到迷宫的终点也就是黄色的方块处就可以了。
public class Maze {
public static void main(String[] args) {
//1.创建地图
int[][] map = createMap(10, 10);
//2.打印地图
System.out.println("初始化地图:");
displayMap(map);
//3.走迷宫
walkMap(map, 1, 1);
//4.打印地图
System.out.println("走迷宫打印:");
displayMap(map);
}
//创建地图
//代码省略
//打印地图
//代码省略
/**
* 走迷宫
*
* @param map 要走的地图
* @param x 起始位置x坐标
* @param y 起始位置y坐标
* @return
*/
public static boolean walkMap(int[][] map, int x, int y) {
//如果走出迷宫,则返回true
if (map[8][8] == 2) {
return true;
}
//如果没有走出,则继续走迷宫
if (map[x][y] == 0) {
//假定该点可以走
map[x][y] = 2;
//按照策略继续走
if (walkMap(map, x + 1, y)) {
//往下走
return true;
} else if (walkMap(map, x, y + 1)) {
//往右走
return true;
} else if (walkMap(map, x - 1, y)) {
//往上走
return true;
} else if (walkMap(map, x, y - 1)) {
//往左走
return true;
} else {
//走不通
map[x][y] = 3;
return false;
}
}
//如果这个方块不能再走(如:1遇墙、2已走过、3走不通)
else {
return false;
}
}
}
初始化地图:
1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 1 1 1 0 0 0 0 0 1
1 0 0 0 0 0 1 1 1 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1 1
走迷宫打印:
1 1 1 1 1 1 1 1 1 1
1 2 0 0 0 0 0 0 0 1
1 2 0 0 0 0 0 0 0 1
1 2 2 2 2 0 0 0 0 1
1 1 1 1 2 0 0 0 0 1
1 0 0 0 2 0 1 1 1 1
1 0 0 0 2 0 0 0 0 1
1 0 0 0 2 0 0 0 0 1
1 0 0 0 2 2 2 2 2 1
1 1 1 1 1 1 1 1 1 1
我们发现程序已经找到了出去迷宫的路了,那一条全是2的路就是赶往出口的路,当然了,你选择的行走策略不一样这个结果也有可能会不一样,我们目前选择的是下->右->上->左,而如果你想要找到路径最小的一条,那就需要把上边所有的行走策略全部走一遍,才能找到最小的一条,这里就不演示了。
4.2、八皇后
八皇后问题(Eight queens),是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出的问题,是回溯算法的典型案例。
问题表述为:在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转,和对角线对称变换的摆法看成一类,共有42类。计算机发明后,有多种计算机语言可以编程解决此问题。
解决八皇后的具体思路:
- 第一个皇后先放第一行第一列。
- 第二个皇后放在第二行第一列、然后判断是否 OK, 如果不 OK,继续放在第二列、第三列、依次把所有列都放完,找到一个合适。
- 继续第三个皇后,还是第一列、第二列……直到第 8 个皇后也能放在一个不冲突的位置,算是找到了一个正确解,然后输出当前8个皇后的位置。
- 当得到一个正确解时,在栈回退到上一个栈时,就会开始回溯,即将第一个皇后,放到第一列的所有正确解, 全部得到。
- 然后回头继续第一个皇后放第二列,后面继续循环执行 1,2,3,4 的步骤,直到找到所有的解。
在这个过程中,如何判断是否在同一行、同一列比较容易判断,但是如何判断在同一斜线是一个麻烦的问题,假设一个点A的坐标是[ a , b ],那么和该点在同一斜线上的点A有四种分别是:
![]()
前两种点横纵坐标相减和A点横纵坐标相减后一样,后两种点横纵坐标相加和A点横纵坐标相加一样。
因此,根据这个我们就可以很方便的判断两个点是否在同一斜线上,只要两个点横纵坐标相加结果相等或者相减结果相等,就可以判断两个点在同一斜线上。
public class EightQueens {
private static int max = 8; //代表8个皇后的数量
private static int[] arr = new int[8]; //代表8个皇后的下标
public static void main(String[] args) {
check(0);
}
//开始摆放八个皇后
public static void check(int n) {
//如果n=8则表明8个皇后已经放好,放好了就直接输出数组信息
if (n == max) {
print();
return;
}
//从当前行的第一列(0)开始逐一放八皇后并判断该皇后是否合法
for (int i = 0; i < max; i++) {
//把当前列下标放到对应皇后的下标
arr[n] = i;
//下标是放好了但是合不合法需判断
if (judge(n)) {
check(n + 1);
}
}
}
//判断位置是否合法
public static boolean judge(int n) {
//i代表皇后下标
for (int i = 0; i < n; i++) {
//array[n] == array[i]代表:第n个皇后和第i个皇后是否在同一列
//这里不用判断是不是在同一行,因为完全没有必要,8个皇后分别在8行上
//Math.abs(n - i) == Math.abs(array[n] - array[i])代表:第n个皇后和第i个皇后是否在同一斜线
if (arr[n] == arr[i] || Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
//输出8个皇后的位置
public static void print() {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
0 4 7 5 2 6 1 3
0 5 7 2 6 3 1 4
0 6 3 5 7 1 4 2
0 6 4 7 1 3 5 2
1 3 5 7 2 0 6 4
1 4 6 0 2 7 5 3
1 4 6 3 0 7 5 2
1 5 0 6 3 7 2 4
1 5 7 2 0 3 6 4
1 6 2 5 7 4 0 3
1 6 4 7 0 3 5 2
1 7 5 0 2 4 6 3
2 0 6 4 7 1 3 5
2 4 1 7 0 6 3 5
2 4 1 7 5 3 6 0
2 4 6 0 3 1 7 5
2 4 7 3 0 6 1 5
2 5 1 4 7 0 6 3
2 5 1 6 0 3 7 4
2 5 1 6 4 0 7 3
2 5 3 0 7 4 6 1
2 5 3 1 7 4 6 0
2 5 7 0 3 6 4 1
2 5 7 0 4 6 1 3
2 5 7 1 3 0 6 4
2 6 1 7 4 0 3 5
2 6 1 7 5 3 0 4
2 7 3 6 0 5 1 4
3 0 4 7 1 6 2 5
3 0 4 7 5 2 6 1
3 1 4 7 5 0 2 6
3 1 6 2 5 7 0 4
3 1 6 2 5 7 4 0
3 1 6 4 0 7 5 2
3 1 7 4 6 0 2 5
3 1 7 5 0 2 4 6
3 5 0 4 1 7 2 6
3 5 7 1 6 0 2 4
3 5 7 2 0 6 4 1
3 6 0 7 4 1 5 2
3 6 2 7 1 4 0 5
3 6 4 1 5 0 2 7
3 6 4 2 0 5 7 1
3 7 0 2 5 1 6 4
3 7 0 4 6 1 5 2
3 7 4 2 0 6 1 5
4 0 3 5 7 1 6 2
4 0 7 3 1 6 2 5
4 0 7 5 2 6 1 3
4 1 3 5 7 2 0 6
4 1 3 6 2 7 5 0
4 1 5 0 6 3 7 2
4 1 7 0 3 6 2 5
4 2 0 5 7 1 3 6
4 2 0 6 1 7 5 3
4 2 7 3 6 0 5 1
4 6 0 2 7 5 3 1
4 6 0 3 1 7 5 2
4 6 1 3 7 0 2 5
4 6 1 5 2 0 3 7
4 6 1 5 2 0 7 3
4 6 3 0 2 7 5 1
4 7 3 0 2 5 1 6
4 7 3 0 6 1 5 2
5 0 4 1 7 2 6 3
5 1 6 0 2 4 7 3
5 1 6 0 3 7 4 2
5 2 0 6 4 7 1 3
5 2 0 7 3 1 6 4
5 2 0 7 4 1 3 6
5 2 4 6 0 3 1 7
5 2 4 7 0 3 1 6
5 2 6 1 3 7 0 4
5 2 6 1 7 4 0 3
5 2 6 3 0 7 1 4
5 3 0 4 7 1 6 2
5 3 1 7 4 6 0 2
5 3 6 0 2 4 1 7
5 3 6 0 7 1 4 2
5 7 1 3 0 6 4 2
6 0 2 7 5 3 1 4
6 1 3 0 7 4 2 5
6 1 5 2 0 3 7 4
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
第五章 分治算法介绍
分治算法(divide and conquer algorithm)又称分治法,他的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分解目标完成程序算法,简单问题可用二分法完成。利用分治策略求解时,所需时间取决于分解后子问题的个数、子问题的规模大小等因素,而二分法,由于其划分的简单和均匀的特点,是经常采用的一种有效的方法,例如二分法检索。
当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止,这就是分治策略的基本思想。
第六章 分治算法应用
6.1、汉诺塔
法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔(Tower of Hanoi),又称河内塔。
不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
不管这个传说的可信度有多大,如果考虑一下把64片金片,由一根针上移到另一根针上,并且始终保持上小下大的顺序,这需要多少次移动呢?假设有n片,移动次数是f(n),显然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时,需要移动18446744073709551615次。假如每秒钟一次,那就是18446744073709551615秒。这表明移完这些金片需要5845.42亿年以上,而地球存在至今不过45亿年,太阳系的预期寿命据说也就是数百亿年。真的过了5845.42亿年,不说太阳系和银河系,至少地球上的一切生命,连同梵塔、庙宇等,都早已经灰飞烟灭。
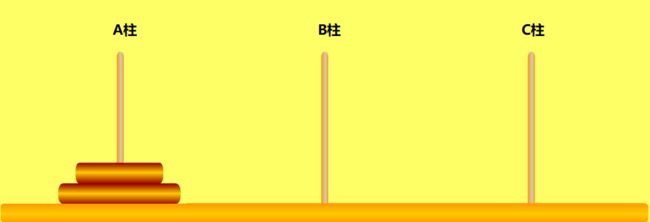
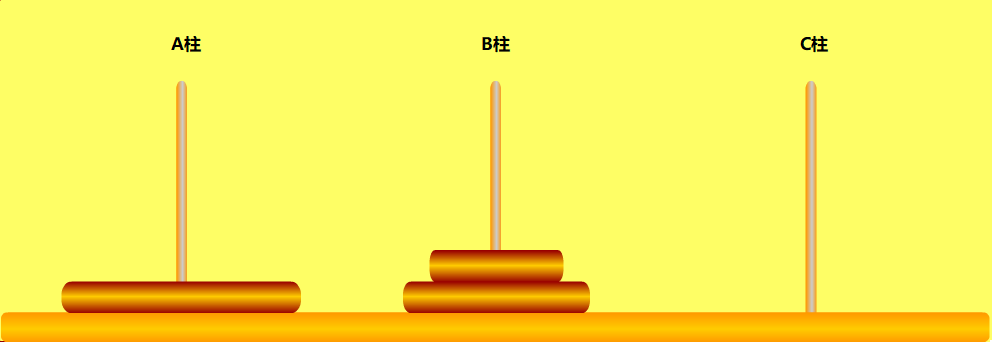
当n=1时,我们直接把这个金片由A柱移动到C柱即可。
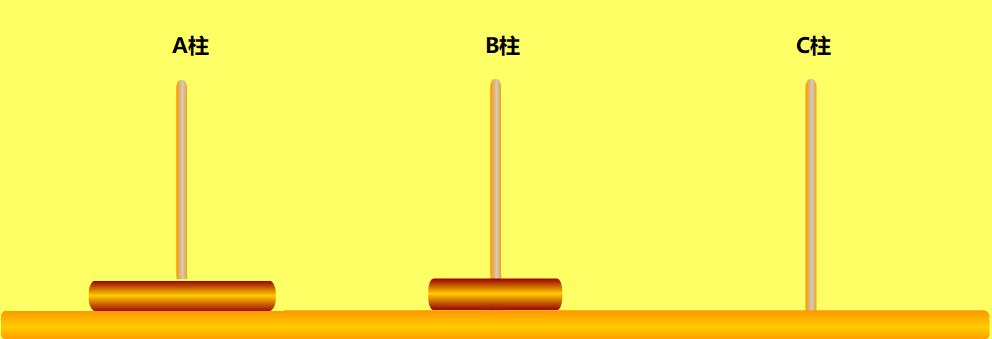
当n=2时,我们首先把最小的金片由A柱移动到B柱,然后把A柱的金片移动到C柱,最后把B柱最小的金片移动到C柱。
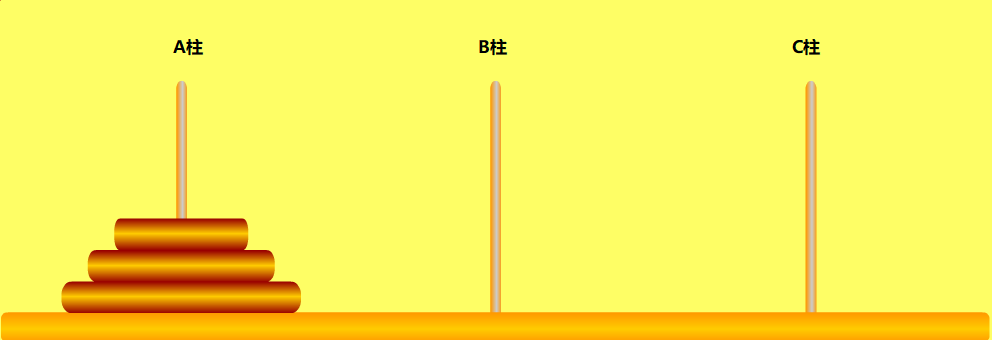
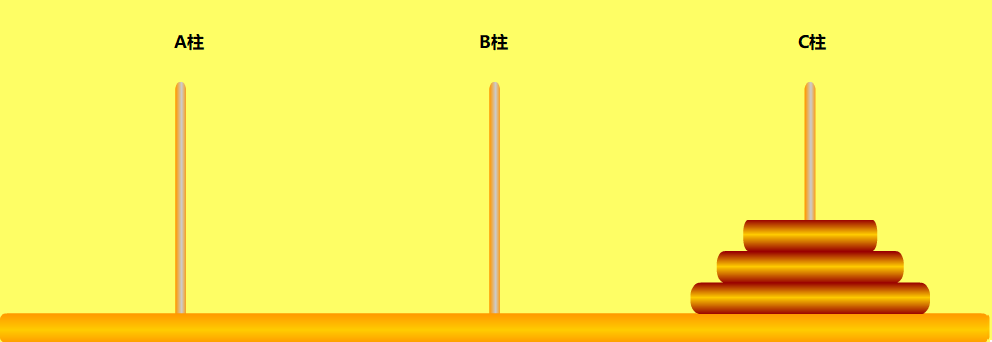
当n=3时,这时候步骤比较多,我就直接贴出移动步骤图了。
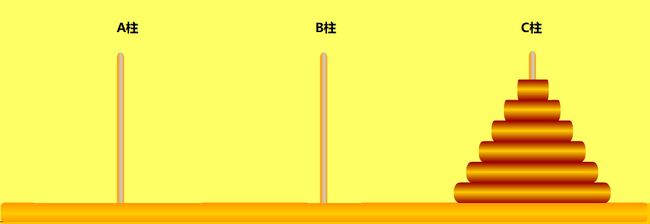
当n=k时,这时候我们会发现移动盘子的步骤越来越复杂,我们可以把这一个问题进行拆分,当n=1和当n=2时,几步就搞定了,要是把这么复杂的问题抽成n=1时,直接把金片由A柱移动到C柱即可,当n=2时,一共三步的事情,那我们有没有一种可能,当n大于或者等于2的时候,我们把一堆金片分成两部分,最顶上的最小的那一片是一部分,其余剩下的是另外一部分。把第二部分看成一个整体来进行移动,具体细节不用管,因为我们会递归调用,计算机会帮我们逐渐将问题进行分解,最后分解成两部分的情况,然后我们就按照n=2这种情况来进行处理。
上边讲解了很多,但是真正实现的代码却并不多,比较容易实现,代码如下:
public class Hanoi {
public static void main(String[] args) {
int n = 3;//我们这里金片假设为3片
hanoi(n, 'A', 'B', 'C');
}
public static void move(char from, char to) {
System.out.printf("%c to %c\n", from, to);
}
public static void hanoi(int n, char a, char b, char c) {
//当只剩下一个金片的时候直接从A柱移动到C柱
if (n == 1) {
move(a, c);
}
//当n>=2时就拆成两部分(n-1)代表第二部分
else {
//将第二部分由A柱移动到B柱
hanoi(n - 1, a, c, b);
//将第一部分由A柱移动到C柱
move(a, c);
//将第二部分由B柱移动到C柱
hanoi(n - 1, b, a, c);
}
}
}
A to C
A to B
C to B
A to C
B to A
B to C
A to C
6.2、棋盘覆盖
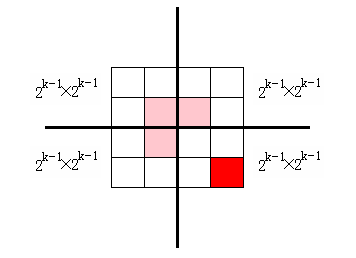
在一个2k×2k (k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为特殊方格。显然,特殊方格在棋盘中可能出现的位置有4k种,因而有4k种不同的棋盘,以下是几种情况的图示。棋盘覆盖问题要求用4种不同形状的L型骨牌覆盖给定棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
首先我们通过观察这些棋盘会发现这是一个四四方方的正方形,并且边长是2的倍数,我们可以通过这一点进行入手,当k非常大的时候,我们自己可能用手写不出来,但是,当k=1时,也就是一个2×2的棋盘,正好可以使用4种L型骨牌中的一种刚好把棋盘覆盖,我们是不是可以这么想,无论你的棋盘有多大,通过不停的二分法,将一个大的棋盘拆分成无数个2×2的棋盘,也就是分而治之,这完全符合分治算法的理念。
当k=2时,我们再来分析一下,在棋盘里只有一块特殊的方格,而且棋盘的大小也比较特殊,2的K次方,非常适合切分成一半。又因为棋盘是个方形的,所以思路可以使将棋盘分成大小相同的四份。当我们将有特殊方格的棋盘分割成4个相同的子棋盘时,4个棋盘分成两类:有特殊方格和没有特殊方格。我们用到的L型骨牌刚好是三个方格的,也就是说可以用一个L型骨牌将其余的三个没有特殊方格的棋盘变成有特殊方格的。
在进行算法设计的时候,我们首先要明白,这个特殊的方格(红色),在一个棋盘中可能出现的位置有4k种,所以,我们必须自己指定这个特殊方格所在的位置,只要是在这个棋盘中,这个特殊方格都可以存放到任何位置,这里我们使用变量dr代表特殊方格横坐标,变量dc代表特殊方格纵坐标。
public class CheckerBoard {
private static int num = 0; //用于存放L型骨牌编号
private static int[][] arr = new int[100][100]; //用于存放棋盘数组信息
public static void main(String[] args) {
//设置棋盘大小
int k = 2;
int size = (int) Math.pow(2.0, k);
//开始棋牌覆盖
checkerBoard(0, 0, size - 1, size - 1, size);
//打印二维数组
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
/**
* 棋盘覆盖
*
* @param tr 当前棋盘左上角的行号
* @param tc 当前棋盘左上角的列号
* @param dr 特殊方格所在的行号
* @param dc 特殊方格所在的列号
* @param size 当前棋盘的大小2^k
*/
public static void checkerBoard(int tr, int tc, int dr, int dc, int size) {
int s, t; //临时变量
if (size == 1) return; //临界条件
s = size / 2; //分割棋盘
t = ++num; //骨牌编号
//覆盖左上角子棋盘
if (dr < tr + s && dc < tc + s) {
//特殊方格在此棋盘中
checkerBoard(tr, tc, dr, dc, s);
} else {
//此棋盘中无特殊方格,用t号L型骨牌覆盖右下角
arr[tr + s - 1][tc + s - 1] = t;
//覆盖其余方格
checkerBoard(tr, tc, tr + s - 1, tc + s - 1, s);
}
//覆盖右上角子棋盘
if (dr < tr + s && dc >= tc + s) {
//特殊方格在此棋盘中
checkerBoard(tr, tc + s, dr, dc, s);
} else {
//此棋盘中无特殊方格,用t号L型骨牌覆盖左下角
arr[tr + s - 1][tc + s] = t;
//覆盖其余方格
checkerBoard(tr, tc + s, tr + s - 1, tc + s, s);
}
//覆盖左下角子棋盘
if (dr >= tr + s && dc < tc + s) {
//特殊方格在此棋盘中
checkerBoard(tr + s, tc, dr, dc, s);
} else {
//此棋盘中无特殊方格,用t号L型骨牌覆盖右上角
arr[tr + s][tc + s - 1] = t;
//覆盖其余方格
checkerBoard(tr + s, tc, tr + s, tc + s - 1, s);
}
//覆盖右下角子棋盘
if (dr >= tr + s && dc >= tc + s) {
//特殊方格在此棋盘中
checkerBoard(tr + s, tc + s, dr, dc, s);
} else {
//此棋盘中无特殊方格,用t号L型骨牌覆盖左上角
arr[tr + s][tc + s] = t;
//覆盖其余方格
checkerBoard(tr + s, tc + s, tr + s, tc + s, s);
}
}
}
2 2 3 3
2 1 1 3
4 1 5 5
4 4 5 0