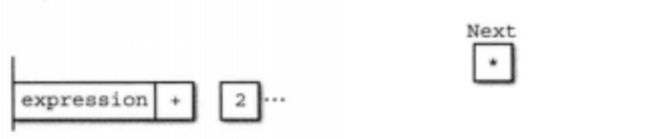借助yacc和lex自制计算器——《自制编程语言》一

《自制编程语言》学习记录，内容基本是摘抄原书

其实原书并不是从头讲怎么写一个计算器的，而是上来就给了代码，对着代码讲解。计算器代码的名字为mycalc，内部完全使用double进行运算。

1.基础概念介绍

1.1 编程语言的语法处理一般有以下的过程：

1.1.1 词法分析

    将源代码分割成若干个记号(token)的处理。

1.1.2 语法分析

    即从记号构建分析树（parse tree）的处理。分析树也叫作语法树（syntax tree）或抽象语法树（abstract syntax tree, AST）。

1.1.3 语义分析

    经过语法分析生成的分析树，并不包含数据类型等语义信息。因此在语义分析阶段，会检查程序中是否含有语法正确但是存在逻辑问题的错误。

1.1.4 生成代码

    如果是C语言等生成机器码的编译器或Java这样生成字节码的编译器，在分析树构建完毕后悔进入代码生成阶段。

比如如下的代码：

if (a == 10) {
    printf("hoge\n");
} else {
    printf("piyo\n");
}

执行词法分析后，将被分割成如下图所示的记号(token):

对此进行语法分析后构建的分析树如下图：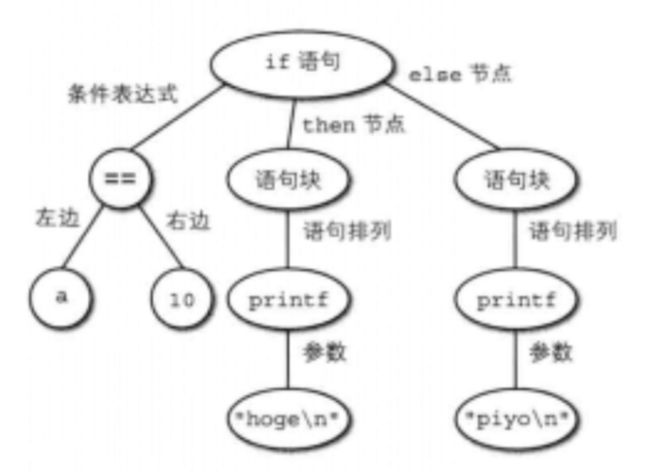

执行词法分析的程序称为 词法分析器（lexical analyzer）， lex就是根据词法规则自动生成词法分析器
执行语法分析的程序称为 解析器（parser）， yacc就是能根据语法规则自动生成解析器的程序
yacc和 lex在mac上已经预装。

1.2 lex：

    lex 是自动生成词法分析器的工具，通过输入扩展名为.l的文件，输出词法分析器的C语言代码。
    词法分析器是将输入的字符串分割成记号的程序，因此必须首先定义mycalc所用到的记号。
    mycalc所用到的记号包括如下：
      ○ 运算符。在mycalc中可以使用四则运算，即+、-、*、\。
      ○ 整数。如1、2、3等。
      ○ 实数。如123.456等。
      ○ 换行符。一个算式输入后，接着输入换行符就会执行计算，因此这里的换行符也应设置为记号

    在lex中，使用正则表达式定义记号。

1.3 yacc：

    yacc是自动生成语法分析器的工具，输入扩展名为.y的文件，就会输出语法分析器的C语言代码。

2.试做一个计算器

mycalc的实际运行效果如下（%是命令提示符）：

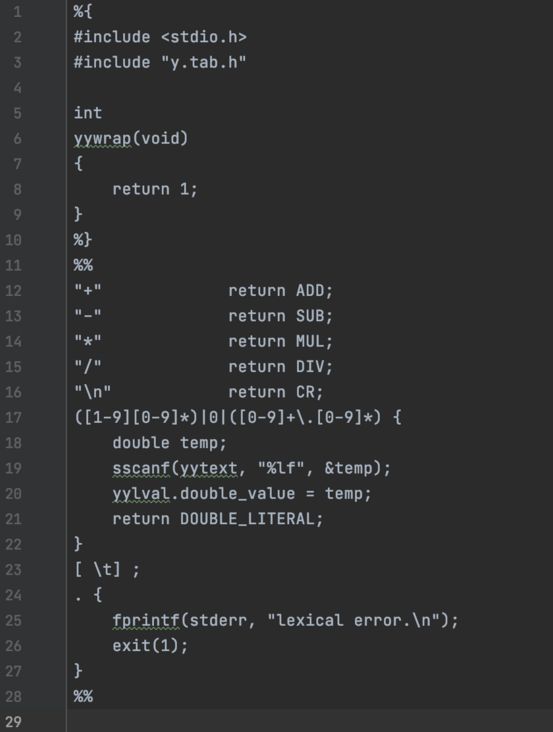
2.1 为mycalc所编写的输入文件mycalc.l如下（用lex解析）：

• 第11行%%，此行之前的部分叫作定义区块。在定义区块内，可以定义初始状态或者为正则表达式命名。
• 第2行到第9行，使用%{和%}包裹的部分，是想让生成的词法分析器将这个部分代码原样输出。后续程序所需的头文件等都包含在这里。比如第3行用#include包含进来的y.tab.h头文件，就是之后yacc自动生成的头文件。下面的ADD、SUB、MUL、DIV、CR、DOUBLE_LITERAL等都是在y.tab.h中用#define定义的宏。

• 第5行到第9行定义了一个名为yywrap()的函数。如果没有这个函数的话，就必须手动链接lex的库文件。
• 第12行到第27行是规则区块。这一部分是使用正则表达式*去描述记号。

在规则区块中遵循如下的书写方式：一个正则表达式的后面紧跟若干个空格，后接C代码。如果输入的字符串匹配正则表达式，则执行后面的C代码。

• 第12行到第16行，找到四则运算符以及换行符，然后通过return返回其特征符（就是在y.tab.h的宏定义）。

上面提到很多次 记号（token），包含三部分含义：

对于 +或 -这样的记号来说，只需要关注其记号种类就可以了，而如果 DOUBLE_LITERAL记号，记号的种类和值都必须传递给解析器

• 第17行的正则表达式是一个匹配“数值”的表带是。表达式匹配成功的结果（即上面列举的记号三要素），“记号的原始字符”会在相应的动作中被名为yytext的全局变量引用。并进一步使用第19行的sscanf()解析

关于第17行正则表达式的解释见 这里

• 第23行的正则表达式[ \t]是对空格以及制表符进行匹配，对应动作为空，因此可以忽略每一行的空白字符。
• 第24行的 .会匹配任意一个字符，这里用于检测是否输入了程序不允许的字符。
• 第28行的%%表示规则区块的结束，这之后的代码被称为用户代码区块。用户代码区块可以编写任意的C代码。

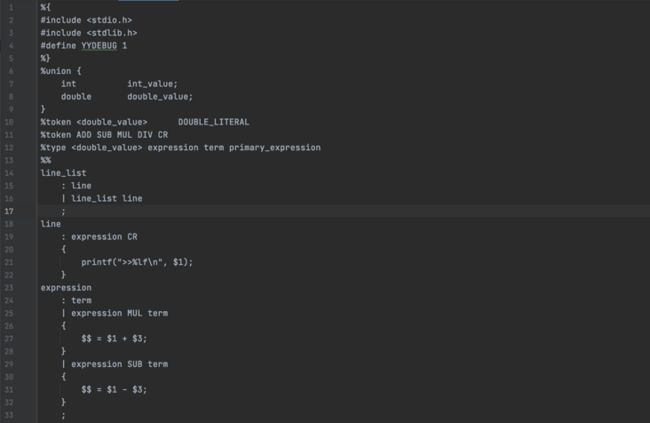
2.2 为mycalc所辨析的输入文件mycalc.y如下（用yacc解析）：

• 第1行到第5行与lex相同，使用%{ %}包裹了一些C代码
• 第4行有一句#define YYDEBUG 1，这样将全局变量yydebug设置为一个非零值后会开启Debug模式，可以看到程序运行中语法分析的状态。
• 第6行到第9行声明了记号以及非终结符的类型。非终结符是由多个记号共同构成，即代码证的line_list、line、expression、term这些部分。为了分割非终结符，非终结符最后都会以一个特殊的记号结尾。这种记号称作终结符
• 第10行到第11行是记号的声明。myclac所用到的记号类型都在这里定义。ADD、SUB、MUL、DIV、CR等记号只需要包含记号的类型就可以，而值DOUBLE_LITERAL的记号，其类型被指定为。这里的double_value是来自上面代码中%union集合的一个成员名（第8行）。
• 第12行声明了非终结符的类型。
• 第13行的%%是分界，之后的是规则区块。yacc的规则区块由语法规则以及C语言编写的相应动作两部分构成。

语法规则

    在yacc中，会使用类似BNF(巴克斯范式)的规范来编写语法规则。将上图的规则代码抽出并注释如下：

// 语法规则代码 2-0
line_list                   /* 多行的规则 */
    : line                  /* 单行 */
    | line_list line        /* 或者是一个多行后接单行 */
    ;
line                        /* 单行的规则 */
    : expression CR         /* 一个表达式后接换行符 */
    ;
expression                  /* 表达式的规则 */
    : term                  /* 和项 */
    | expression MUL term   /* 或 表达式 + 和项 */
    | expression SUB term   /* 或 表达式 - 和项 */
    ;
term                        /* 和项的规则 */
    : primary_expression            /* 一元表达式 */
    | term MUL primary_expression   /* 或 和项 * 一元表达式 */
    | term DIV primary_expression   /* 或 和项 / 一元表达式 */
    ;
primary_expression          /* 一元表达式的规则 */
    : DOUBLE_LITERAL        /* 实数的字面常量 */
    ;

   为了看得更清楚，可以将愈发规则简化成下面的格式：

A
 : B C
 | D
 ;

    即A的定义是B与C的组合，或者为D。
    第1行到第4行的书写方式，表示该语法规则在程序中可能会出现一次以上。mycalc中，输入一行语句然后回车后会执行运算，之后还可以继续输入语句，所以设计成支持出现一次以上的模式。

请注意上面的计算器语法规则，语法规则本身就包含了运算符的优先顺序以及结合规律。如果不考虑运算法的优先顺序，上文的语法规则应该如下：

expression                  /* 表达式的规则 */
    : term                  /* 和项 */
    | expression ADD term   /* 或 表达式 + 和项 */
    | expression SUB term   /* 或 表达式 - 和项 */
    | expression MUL term   /* 或 表达式 * 和项 */
    | expression DIV term   /* 或 表达式 / 和项 */
    ;
primary_expression          /* 一元表达式的规则 */
    : DOUBLE_LITERAL        /* 实数的字面常量 */
    ;

yacc解析流程

    对照语法规则代码 2-0跟踪下解析1 + 2 * 3的执行流程

   首先，yacc生成的解析器会保存在程序内部的栈。在这个栈中，记号会像俄罗斯方块中的方块一样，一个个堆积起来。
    词法分析器分出来的记号（最初是1）会由右边入栈并堆积到左边。

像这样一个记号进入并堆积的过程叫作 移进（shift)

    mycalc所有的计算都是采用double类型，所以记号1即是DOUBLE_LITERAL。当记号进入的同时，会触发我们定义的规则:

primary_expression
    : DOUBLE_LITERAL
    ;

    然后记号会被换成primary_expression。

类似这样触发某个规则并进行置换的过程叫作 归约（reduce）

    primary_expression进一步触发规则：

term
    : primary_expression

    然后被归约成term。

    再进一步根据规则：

expression
    : term

    最终被归约为一个expression。

    接下来，记号+进入，在进入过程中，由于没匹配到任何一个规则，所以只进行移进不做任何归约。

    接下来是记号2进入。

    经过上述同样的规则，记号2(DOUBLE_LITERAL)会经过primary_expression被归约为term。

    这里记号2本应该匹配到如下的规则：

expression
    | expression ADD term

    yacc预先读取下一个要进入的记号，这里我们主动下一个进入的会是*，因此应当考虑到记号2会匹配到term规则的可能性。

term
    | term MUL primary_expression

    归约完毕后再一次移进。

    接下来记号3进入。

    被归约为primary_expression后，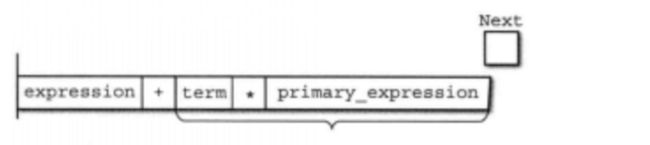

    term、*、primary_expression这一部分将匹配规则：

term
    | term MUL primary_expression

    被归约为term。

    之后，expression、+、term匹配规则：

expression
    | expression ADD term

    最终被归约为expression。

    每次触发归约时，yacc都会执行该规则的相应动作。比如乘法对应的执行规则：

term
    | term MUL primary_expression 
    {
        $$ = $1 * $3;
    }

    $1、$3的意思分别保存了term与primary_expression的值。即yacc输出解析器的代码时，栈中相应位置的元素会转换为一个能表达元素特征的数组引用。这里的$2是乘法运算符（*），并不存在记号值，所以这里引用$2的话会报错。
    $1与$3进行乘法运算，然后将结果赋给$$，这个结果值保留在栈中。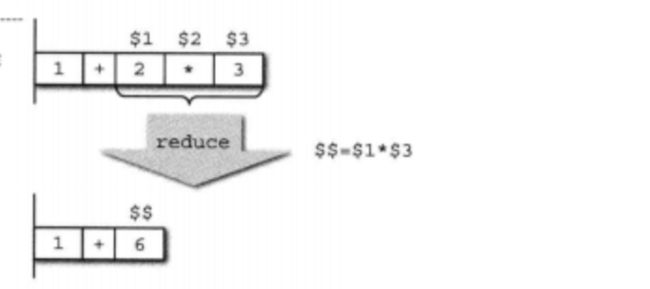

如果没有书写动作，yacc会自动补全一个 { $$ = $1 }的动作。当 DOUBLE_LITERAL被归约为 primary_expression、 primary_expression被归约为 term的时候， DOUBLE_LITERAL包含的数值也会被继承。

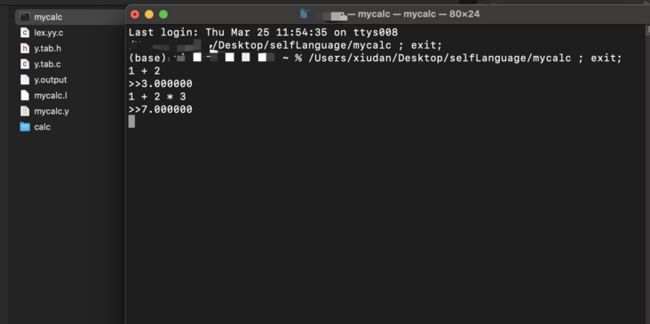
2.3 生成执行文件

    mac下按顺序执行如下命令，就会输出名为mycalc的执行文件

yacc -dv mycalc.y   // 运行yacc
lex mycalc.l       // 运行lex
cc -o mycalc y.tab.c lex.yy.c  //使用C编译器编译

注意：按照上述的命令，在新款的MacOS上在最后一步编译时会报错， 类似问题看这。
所以想要正常编译我们需要改一下mycalc.y的前面部分：

%{
#include 
#include 
#define YYDEBUG 1
int yylex();  // 增加声明
int yyerror(const char *str); // 增加声明
%}

    最终的可执行文件打开之后如下图：

    整个过程会生成若干文件：

    y.tab.c中包含yacc生成的语法分析器的代码，lex.yy.c是词法分析器的代码。y.tan.h是为了将mycalc.y中定义的记号及联合体(union)传递给lex.yy.c。

2.4 冲突

    实际用yacc试做一下解析器，可能会被冲突（conflict）困扰。所谓冲突，就是遇到语法中模糊不清的地方时，yacc报出呃错误。
    比如C语言的if语句，就有很明显的语法模糊问题：

if (a == 0)
    if (b== 0)
        printf(在这里a和b都为0n);
else 
    printf(这里a非0n);

    上面的代码中，else对应的if是不清晰的。这就会引起冲突。

yacc运行时，遇到下面任意一种情况都会发生冲突。

1. 同时可以进行多个归约。称为归约/归约冲突。
2. 满足移进的规则，同时又满足归约的规则。称为移进/归约冲突

即便发生冲突，yacc仍会生成解析器。如果存在归约/归约冲突，则优先匹配前面的语法规则，移进/归约冲突则会优先匹配移进规则。

    将mycalc.y做如下修改：

// 原代码
expression
    : term
    | expression ADD term

    更为：

// 原代码
expression
    : term
    | expression MUL term

    变更后悔产生3个移进/归约冲突：

yacc -dv mycalc.y            
conflicts: 3 shift/reduce

    再看y.output文件，前半部分：

Terminals which are not used  //没有使用 ADD 的警告
   ADD
State 5 conflicts: 1 shift/reduce  // 冲突信息（见下文）
State 14 conflicts: 1 shift/reduce
State 15 conflicts: 1 shift/reduce
Grammar
    0 $accept: line_list $end
    1 line_list: line
    2          | line_list line
    3 line: expression CR
    4 expression: term
    5           | expression MUL term
    6           | expression SUB term
    7 term: primary_expression
    8     | term MUL primary_expression
    9     | term DIV primary_expression
   10 primary_expression: DOUBLE_LITERAL
Terminals, with rules where they appear

    mycalc.y中使用|（竖线，表示或）书写下面的语法规则:

1 line_list: line
2          | line_list line

    实际上与下面的写法一样：

1 line_list: line
2 line_list: line_list line

    y.output文件中会给每一行规则附上编号。

    上面的规则0，是yacc自动附加的规则，$accept代表输入的内容，$end代表输入结束。

    y.output文件的后半部分会将解析器可能遇到的所有"状态"全部列举出来：

state 0
    0 $accept: . line_list $end
    DOUBLE_LITERAL  shift, and go to state 1
    line_list           go to state 2
    line                go to state 3
    expression          go to state 4
    term                go to state 5
    primary_expression  go to state 6
state 1
   10 primary_expression: DOUBLE_LITERAL .
    $default  reduce using rule 10 (primary_expression)
state 2
    0 $accept: line_list . $end
    2 line_list: line_list . line
    $end            shift, and go to state 7
    DOUBLE_LITERAL  shift, and go to state 1
    line                go to state 8
    expression          go to state 4
    term                go to state 5
    primary_expression  go to state 6
state 3
    1 line_list: line .
    $default  reduce using rule 1 (line_list)
state 4
    3 line: expression . CR
    5 expression: expression . MUL term
    6           | expression . SUB term
    SUB  shift, and go to state 9
    MUL  shift, and go to state 10
    CR   shift, and go to state 11
state 5
    4 expression: term .
    8 term: term . MUL primary_expression
    9     | term . DIV primary_expression
    MUL  shift, and go to state 12
    DIV  shift, and go to state 13
    MUL       [reduce using rule 4 (expression)]
    $default  reduce using rule 4 (expression)
    
下略

    yacc生成解析器的阶段，将解析器所能遇到的所有状态都列举出来，并做成一个解析对照表（Parse Table），表中记录了“状态A下某幢记号进入后会转换成状态B”这样的映射关系。

    根据y.output开头的信息：

State 5 conflicts: 1 shift/reduce
State 14 conflicts: 1 shift/reduce
State 15 conflicts: 1 shift/reduce

    可以看到state 5引起了冲突：

state 5
    4 expression: term .
    8 term: term . MUL primary_expression
    9     | term . DIV primary_expression
    MUL  shift, and go to state 12
    DIV  shift, and go to state 13
    MUL       [reduce using rule 4 (expression)]
    $default  reduce using rule 4 (expression)

    第一行state 5为状态编号，接下来的3行是y.output前半部分中输出的语法规则（4，8，9）。语法规则中间的.代表记号在当前规则下呗转换到哪个程度。比如state 5状态下，记号最多被转换成term，然后需要等待下一个记号进行归约。

    再下面，记录的是当前状态下，下一个记号进入时如何变化。具体来讲，当MUL(*)记号进入后悔进行移进并转换到state 12，如果进入的是DIV(/)，则进行移进并转移到state 13。

    再下面：

    MUL       [reduce using rule 4 (expression)]

    意思当MUL进入后，可以按照state 4进行归约。这就是移进/归约冲突。

    yacc默认移进优先，所以MUL进入后悔转移到state 12:

state 12
    8 term: term MUL . primary_expression
    DOUBLE_LITERAL  shift, and go to state 1
    primary_expression  go to state 16

    如果是归约的话，参照的规则是这样的:

4 expression: term

    上述演示的一个冲突，正是由于我们将ADD改为MUL后，*运算优先级被降低导致的。

2.5 错误处理

    可以利用yacc的功能给mycalc.y实现一个简单的错误恢复机制：

// 修改后的代码
line
    : expression CR
    {
        printf(">>%lfn", $1);
    }
    | error CR
    {
        yyclearin;
        yyerrok;
    }

这个错误处理的函数，我没能测试出什么结果。所以只放这段代码。

3 结束

    以上结束了一个mycalc计算器的代码流程，编译完之后确实有一个终端计算器。但是实际上代码都是原书提供的，跟着思路走了一遍。还是没能了解太对自制编程语言知识，算是对词法分析等基础概念有点了解。后续会不借助jacc和lex重新制作一个计算器。本文结束。