原文链接:http://tecdat.cn/?p=11974
R2WinBUGS软件包提供了从R调用WinBUGS的便捷功能。它自动以WinBUGS可读的格式写入数据和脚本,以进行批处理(自1.4版开始)。WinBUGS流程完成后,可以通过程序包本身将结果数据读取到R中(这提供了推断和收敛诊断的紧凑图形摘要),也可以使用coda程序包的功能对输出进行进一步分析。
WinBUGS软件可从http://www.mrc-bsu.cam.ac.uk/...。
R是一种“用于数据分析和图形处理的语言”,是一种实现该语言的开放源代码和免费提供的统计软件包,请参见http://www.R-project.org/。 R和R2WinBUGS可从CRAN 获得,即http://CRAN.R-Project.org或其...。 如果可以使用Internet连接,则可以在R命令提示符下键入install.packages(“ R2WinBUGS”)来安装R2WinBUGS。别忘了用library(R2WinBUGS)
例子
学校数据
学术能力测验(SAT)衡量高中生的能力,来帮助大学做出入学决定。 我们的数据来自1970年代后期进行的一项实验,来自八所高中的SAT-V(学业能力测试语言)。SAT-V是由教育测试服务局管理的标准多项选择测试。该服务对所选学校中每所学校的教练计划的效果很感兴趣。
实现
R2WinBUGS软件包的实现非常简单。 main“函数bugs() 由用户调用。原则上,它是对 其中逐步调用的其他几个函数的包,如下:
- bugs.data.inits()写入数据文件' data.txt”和“ inits1.txt”,“ inits2.txt” ...进入 工作目录。
- bugs.script()写入WinBUGS用于批处理的文件“ script.txt”。
- bugs.run()更新WinBUGS注册表 ,调用WinBUGS,并使用 'script.txt' 以批处理模式运行它。
- bugs.sims()如果参数codaPkg已设置为false(默认值)才调用。
否则,bugs()返回存储数据的文件名。例如,这些可以通过打包的coda 导入,该软件包提供了收敛诊断,蒙特卡洛估计的计算,迹线图等功能。
bugs.sims()函数将WinBUGS中的模拟读取到R中,将其格式化,监视收敛,执行收敛检查并计算中位数和分位数。它还为bugs()本身准备输出。
这些功能不由用户直接调用。参数将从bugs()传递给其他函数。
例子
我们将 R2WinBUGS提供的功能应用于示例数据并分析输出。
学校数据
示例数据 :
> schools 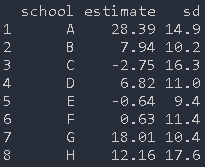
为了对这些数据进行建模,我们使用了Gelman等人提出的分层模型。 我们假设每所学校的观测估计值具有正态分布,且均值theta 和方差tau.y,逆方差为1 =σ.y2,其先验分布在(0,1000)上是均匀的。对于均值theta,我们采用另一个正态分布 平均为mu.theta和逆方差为tau.theta。有关其先验分布,请参见以下WinBUGS代码:
model {
for (j in 1:J)
{
y[j] ~ dnorm (theta[j], tau.y[j])
theta[j] ~ dnorm (mu.theta, tau.theta)
tau.y[j] <- pow(sigma.y[j], -2)
}
mu.theta ~ dnorm (0.0, 1.0E-6)
tau.theta <- pow(sigma.theta, -2)
sigma.theta ~ dunif (0, 1000)
}此模型必须存储在单独的文件中,例如'schools.bug'2,在适当的目录中,例如c:/ schools /。在R中,用户必须准备bugs()函数所需的数据输入。这可以是包含每个数据向量名称的列表,例如
> J <- nrow(schools) 使用这些数据和模型文件,我们可以运行MCMC模拟以获取theta, mu.theta和sigma.theta的估计值。在运行之前,用户必须确定要运行多少个链 (n.chain = 3)和迭代次数(n.iter = 1000)。另外,用户必须指定链的初始值,例如通过编写函数:
> inits <- function(){
+ list(theta = rnorm(J, 0, 100), mu.theta = rnorm(1, 0, 100),
+ sigma.theta = runif(1, 0, 100))
+ }可以开始MCMC模拟,R中的参数bugs.directory必须指向WinBUGS的安装目录。可以通过print(schools.sim)方便地输出school.sim对象中的结果。
对于此示例,将获得类似的结果
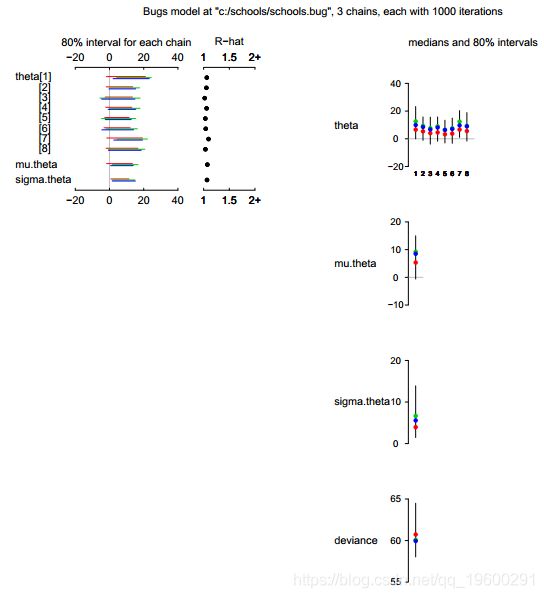
Inference for Bugs model at "c:/schools/schools.bug"
3 chains, each with 1000 iterations (first 500 discarded)
n.sims = 1500 iterations saved
mean sd 2.5% 25% 50% 75% 97.5% Rhat n.eff
theta[1] 11.1 9.1 -3.0 5.0 10.0 16.0 31.8 1.1 39
theta[2] 7.6 6.6 -4.7 3.3 7.8 11.6 21.1 1.1 42
theta[3] 5.7 8.4 -12.5 0.6 6.1 10.8 21.8 1.0 150
theta[4] 7.1 7.0 -6.6 2.7 7.2 11.5 21.0 1.1 42
theta[5] 5.1 6.8 -9.5 0.7 5.2 9.7 18.1 1.0 83
theta[6] 5.7 7.3 -9.7 1.0 6.2 10.2 20.0 1.0 56
theta[7] 10.4 7.3 -2.1 5.3 9.8 15.3 25.5 1.1 27
theta[8] 8.3 8.4 -6.6 2.8 8.1 12.7 26.2 1.0 64
mu.theta 7.6 5.9 -3.0 3.7 8.0 11.0 19.5 1.1 35
sigma.theta 6.7 5.6 0.3 2.8 5.1 9.2 21.2 1.1 46
deviance 60.8 2.5 57.0 59.1 60.2 62.1 66.6 1.0 170
pD = 3 and DIC = 63.8 (using the rule, pD = var(deviance)/2)
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC is an estimate of expected predictive error (lower deviance is better).此外,用户可以通过输入plot(schools.sim)生成结果图。 结果图如图所示。在该图中,左列显示了以下内容的快速摘要:
推论和收敛(所有参数的Rb都接近1.0,表明三个链的良好混合,因此近似收敛);右列显示每组参数的推论。从右栏中可以看到,R2WinBUGS使用 WinBUGS中的参数名称将输出构造为标量,向量和参数数组。