HashMap之Hash解读

HashMap基础源码阅读

最近又看了一下hashMap的源码，发现了一些之前没有关注到的内容，比如Hash为什么要这么设计？后续的很多功能都会基于这个Hash算法进行延伸，比如扩容等等，今天重新再来认识一遍hash的算法。

首先展示代码:

// 构建hash
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
// 计算hash下标
int n = tab.length;
// 将(tab.length - 1) 与 hash值进行&运算
int index = (n - 1) & hash;

这里一共做了3步骤:

先拿到hashCode的值
将hashCode的高16位参与运算
将数组长度与hash做位于运算

首先带着问题来看这一部分代码:

为什么数组长度要 - 1，直接数组长度&key.hash不行吗
为什么右移 16 位，为什么要使用 ^ 位异或?
为什么要使用位与运算代替取模运算？
为什么扩容要按照2倍?数据如何迁移的
为什么大部分 hashcode 方法使用 31?
为什么选择红黑树作为链表过长的替代方案?

1. 为什么数组长度要 - 1，直接数组长度&key.hashCode不行吗

我们这里可以做个试验来看看如果不这么做的情况

log.info("数组长度不-1：{}", 16 & "郭德纲".hashCode());
log.info("数组长度不-1：{}", 16 & "彭于晏".hashCode());
log.info("数组长度不-1：{}", 16 & "李小龙".hashCode());
log.info("数组长度不-1：{}", 16 & "蔡徐鸡".hashCode());
log.info("数组长度不-1：{}", 16 & "唱跳rap篮球鸡叫".hashCode());

log.info("数组长度-1但是不进行异或和>>>16运算：{}", 15 & "郭德纲".hashCode());
log.info("数组长度-1但是不进行异或和>>>16运算：{}", 15 & "彭于晏".hashCode());
log.info("数组长度-1但是不进行异或和>>>16运算：{}", 15 & "李小龙".hashCode());
log.info("数组长度-1但是不进行异或和>>>16运算：{}", 15 & "蔡徐鸡".hashCode());
log.info("数组长度-1但是不进行异或和>>>16运算：{}", 15 & "唱跳rap篮球鸡叫".hashCode());

log.info("数组长度-1并且进行异或和>>>16运算：{}", 15 & ("郭德纲".hashCode()^("郭德纲".hashCode()>>>16)));
log.info("数组长度-1并且进行异或和>>>16运算：{}", 15 & ("彭于晏".hashCode()^("彭于晏".hashCode()>>>16)));
log.info("数组长度-1并且进行异或和>>>16运算：{}", 15 & ("李小龙".hashCode()^("李小龙".hashCode()>>>16)));
log.info("数组长度-1并且进行异或和>>>16运算：{}", 15 & ("蔡徐鸡".hashCode()^("蔡徐鸡".hashCode()>>>16)));
log.info("数组长度-1并且进行异或和>>>16运算：{}", 15 & ("唱跳rap篮球鸡叫".hashCode()^("唱跳rap篮球鸡叫".hashCode()>>>16)));

得到的hash计算结果:

数组长度不-1：0
数组长度不-1：0
数组长度不-1：16
数组长度不-1：16
数组长度不-1：16
-------------------------------------
数组长度-1但是不进行异或和>>>16运算：8
数组长度-1但是不进行异或和>>>16运算：14
数组长度-1但是不进行异或和>>>16运算：8
数组长度-1但是不进行异或和>>>16运算：2
数组长度-1但是不进行异或和>>>16运算：14
-------------------------------------
数组长度-1并且进行异或和>>>16运算：4
数组长度-1并且进行异或和>>>16运算：14
数组长度-1并且进行异或和>>>16运算：7
数组长度-1并且进行异或和>>>16运算：13
数组长度-1并且进行异或和>>>16运算：2

你会发现越往下得到的值越分散，一旦hash冲突过多，就会导致所有的值怼到一个桶下标中，极其不分散。后续转换红黑树会更多，结构更复杂，这对性能有很大的影响。

我们知道HashMap的数组初始长度是16，但最终计算是-1之后的15来做运算的，为什么会这么做呢？

首先明确一点，hashCode函数返回类型是int类型，也就是32位；

之前一直以为数组长度-1是为了防止数组越界。

其实这和它的二进制码和与运算有很大关系

log.info("16的二进制码：{}",Integer.toBinaryString(16));  
//16的二进制码：10000
log.info("15的二进制码：{}",Integer.toBinaryString(15));  
//15的二进制码：1111

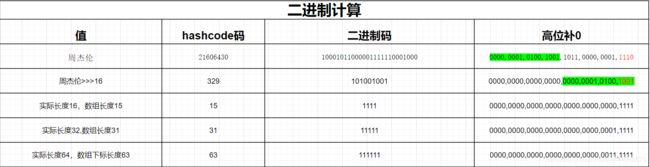
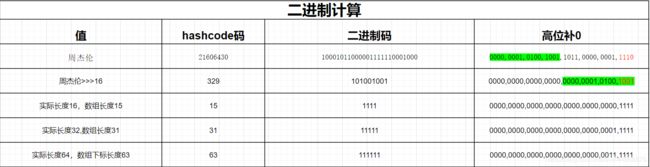
log.info("key的二进制码：{}",Integer.toBinaryString("周杰伦".hashCode()));
//key的二进制码：0000,0001,0100,1001,1011,0000,0001,1110

> &运算规则是第一个操作数的的第n位于第二个操作数的第n位都为1才为1，否则为0

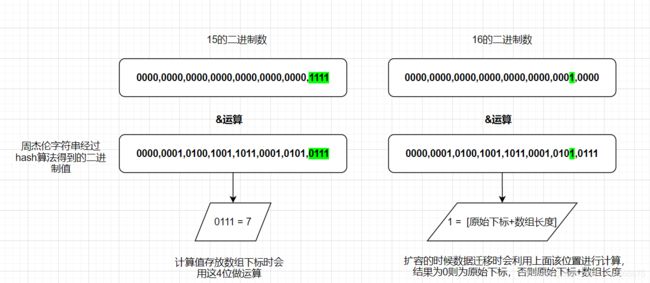
// 如果拿16的二进制码去运算,这里的结果是进行高位补0后的值
0000,0000,0000,0000,0000,0000,0000,1111 -- 15长度的二进制
0000,0000,0000,0000,0000,0000,0001,0000 -- 16长度的二进制
0000,0001,0100,1001,1011,0000,0001,1110 -- 周杰伦的hashcode的二进制
如果两者做&运算你会发现16长度的二进制运算只有倒数第5位才能参与运算,
也就是说得到的可能就两个结果0,16 这碰撞的概率可想而知

从这个案例可以看出15的二进制参与运算的更多，得到的hash结果更均匀。

还有一个参考因素就是这个公式：x mod 2^n = x & (2^n - 1)等于 h & (table.length - 1) ，也是正好切合底层数组的长度总是2的n次方

2. 为什么右移 16 位，为什么要使用 ^ 位异或?

其实上面的案例也关系到了第2个问题，我们发现>>>16之后然后异或之后下标冲突的情况真的减少了，说明这种做法有利于减少hash冲突。然而为什么会减少hash冲突呢?

我们再来一个案例,如果不这么做的话,直接拿hashcode去和长度做与运算的话会发生什么结果呢?

0000,0000,0000,0000,0000,0000,0000,1111 -- 15长度的二进制
0000,0001,0100,1001,1011,0000,0001,1110 -- 周杰伦的hashcode的二进制

我们知道15的二进制码是1111，这个时候拿周杰伦的hashcode直接去运算的话，你会发现他只会拿最后四位做运算。会带来的问题:

一旦后四位相等的，经过位与运算肯定会得到同一个下标，碰撞概率还是会高，这对散列表来说是很严重的。
32位只有最后4位参与运算的话，前面28位都浪费了。

这个时候(h = key.hashCode()) ^ (h >>> 16)这里发挥作用了，它干了什么？
首先它将hashcode的高16位截取过来和hashcode的低16位做异或运算。

|       高位        |     低位      
0000,0001,0100,1001,1011,0000,0001,1110         - 原始hashcode
0000,0000,0000,0000,0000,0001,0100,1001         - 将上面的高16位截取过来之后,作为低位与原始hashcode做一次翻转
------------------1001-----------------         - 后四位结果
1101,0101,1001,1110,0010,0110,1101,1110
0000,0000,0000,0000,1101,0101,1001,1110
------------------1110-----------------

这样就将前面的hashcode给利用起来了，所以：

右移>>>16位就是为了将hashcode的高位截取出来
而^异或运算就是将高位和低位再进行运算得到hash值

总的来说还是为了减少碰撞的概率

3. 为什么要使用与运算代替取模运算？

(leng-1)&hash与hashcode % length的结果是一样的.【上面的公式可以回看一下(h = key.hashCode()) ^ (h >>> 16)】
当长度只有为2的n次方时才满足1的条件，还有就是位运算可以很轻松计算出扩容后下标的值【这里可以往下看】。
很重要的一点就是与运算的效率是高于取模运算的.

4. 为什么扩容要按照2倍?数据如何迁移的?

hash 算法的目的是为了让hash值均匀的分布在桶中（数组），那么，如何做到呢？试想一下，如果不使用 2 的幂次方作为数组的长度会怎么样？
假设我们的数组长度是10，还是上面的公式：

// 这里就是后四位进行计算
1010 & 101010100101001001000 结果：1000 = 8
1010 & 101000101101001001001 结果：1000 = 8
1010 & 101010101101101001010 结果：1010 = 10
1010 & 101100100111001101100 结果：1000 = 8

看到结果我们惊呆了，这种散列结果，会导致这些不同的key值全部进入到相同的插槽中，形成链表，性能急剧下降。

所以说，我们一定要保证 & 中的二进制位全为 1，才能最大限度的利用 hash 值，并更好的散列，只有全是1 ，才能有更多的散列结果。

与运算的特性: 只有当运算的两个值都为1时才为1 , 否则为0

如果是 1010，有的散列结果是永远都不会出现的，比如 0111，0101，1111，1110…….，只要 & 之前的数有 0，对应的 1 肯定就不会出现（因为只有都是1才会为1）。大大限制了散列的范围。

下表也可以说明为什么要以2的倍数：

长度	二进制码
16 - 1 =15	1111
32 - 1 = 31	11111
64 - 1 = 63	111111
长度 * 2 - 1	1111111....

成倍增长的好处就是可以方便扩容.

HashMap扩容的时候会构建一个2倍长度的数组，这个时候需要从老的数组往新的数组进行迁移，它的做法是将当前老数组下标的链表进行遍历，然后根据每个值的hash&oldCap==0满足条件则还是在新的数组中的原索引下标进行存放，不满足则放入原索引下标+oldCap的位置。

比如原始下标为15，老的数组长度oldCap为16，扩容的时候只会迁移到15或者31.
所以只可能存在两个位置，不会在均匀放入其他位置。

如果用二进制表示的话:
假设老的长度为16，那么它的二进制为：10000
计算下标的长度为15，那么它的二进制为：1111

计算描述

总的来说就是:

15是位与运算存放的值
16是用来扩容后新数组计算下标的值

以此类推后续31/32,63/64...

对应这个图去看

对应代码:


Node loHead = null, loTail = null;
Node hiHead = null, hiTail = null;
Node next;
do {
    next = e.next;
    // 将当前值的hash与当前老的数组长度做与运算
    if ((e.hash & oldCap) == 0) {
        if (loTail == null)
            loHead = e;
        else
            loTail.next = e;
        loTail = e;
    }else {
        if (hiTail == null)
            hiHead = e;
        else
            hiTail.next = e;
        hiTail = e;
    }
} while ((e = next) != null);
if (loTail != null) { // 老的原始下标位置
    loTail.next = null;
    newTab[j] = loHead;
}
if (hiTail != null) {// 新的原始下标位置
    hiTail.next = null;
    newTab[j + oldCap] = hiHead;
}

5. 为什么大部分 hashcode 方法使用 31?

选择31是因为可以用移位和减法运算来代替乘法，从而得到更好的性能。

在这里插入图片描述

说到这里你可能已经想到了：31 * num 等价于(num << 5) – num，左移5位相当于乘以2的5次方再减去自身就相当于乘以31，现在的VM都能自动完成这个优化。

位运算是 JVM 里最有效的计算方式：

【左移 <<】左边的最高位丢弃，右边补全0(把 << 左边的数据*2的移动次幂)。
【右移 >>】把>>左边的数据/2的移动次幂。
【无符号右移 >>>】无论最高位是 0 还是 1，左边补齐 0。
所以：31 * i = (i << 5) - i【例如：312=62 转换为 22^5-2=62】

所以总的来说有以下几点:

首先31是质数，可以降低hash冲突的概率
31可以被jvm优化，做位运算的时候效率会很高

6. 为什么选择红黑树作为链表过长的替代方案?

看过源码的同学可能会知道，当桶中链表元素个数大于等于8时，链表转换成树结构；若桶中链表元素个数小于等于6时，树结构还原成链表。

为什么是8?
红黑树的平均查找长度，也就是时间复杂度是log(n)，长度为8，查找长度为log(8)=3，因为2的3次方是8。
链表的平均查找长度为n/2，当长度为8时，平均查找长度为8/2=4，这才有转换成树的必要。
因为log(8)比8/2小，用树结构需要的查找步数更少；

链表长度如果是小于等于6，6/2=3，2

所以最终选择8是从时间复杂度考虑的结果，从8开始用树效率更好。

还有选择6和8，中间有个差值7可以有效防止链表和树频繁转换。假设一下，如果设计成链表个数超过8则链表转换成树结构，链表个数小于8则树结构转换成链表，如果一个HashMap不停的插入、删除元素，链表个数在8左右徘徊，就会频繁的发生树转链表、链表转树，效率会很低。

另外为什么选择红黑树而不是AVL平衡二叉树?

AVL树是一种高度平衡的二叉树，所以查找的非常高，但是，有利就有弊，AVL树为了维持这种高度的平衡，就要付出更多代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用AVL树的代价就有点高了。

红黑树只是做到了近似平衡，并不严格的平衡，所以在维护的成本上，要比AVL树要低。

所以，红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，我们更倾向于这种性能稳定的平衡二叉查找树。

感谢您的阅读，如果有写的不好的地方欢迎指正留言。

以下是参考资料，都写的挺棒的
真正搞懂hashCode和hash算法
史上最详细的 JDK 1.8 HashMap 源码解析
java工程师必知必会的 hashcode 和 hash 算法
为什么HashMap链表长度超过8会转成树结构？
在Java8中为什么要使用红黑树来实现的HashMap？