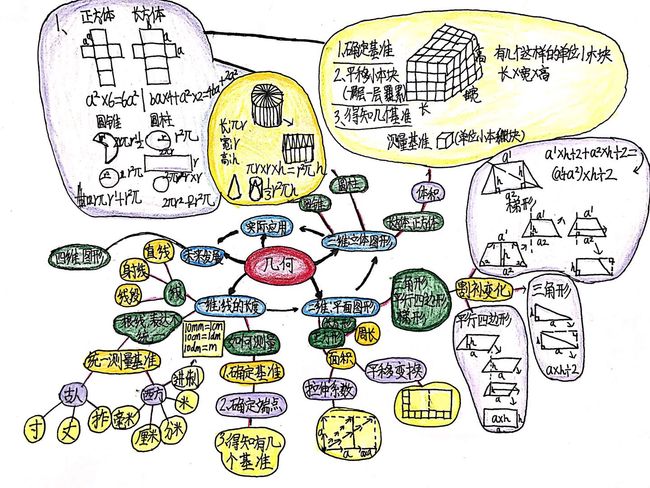
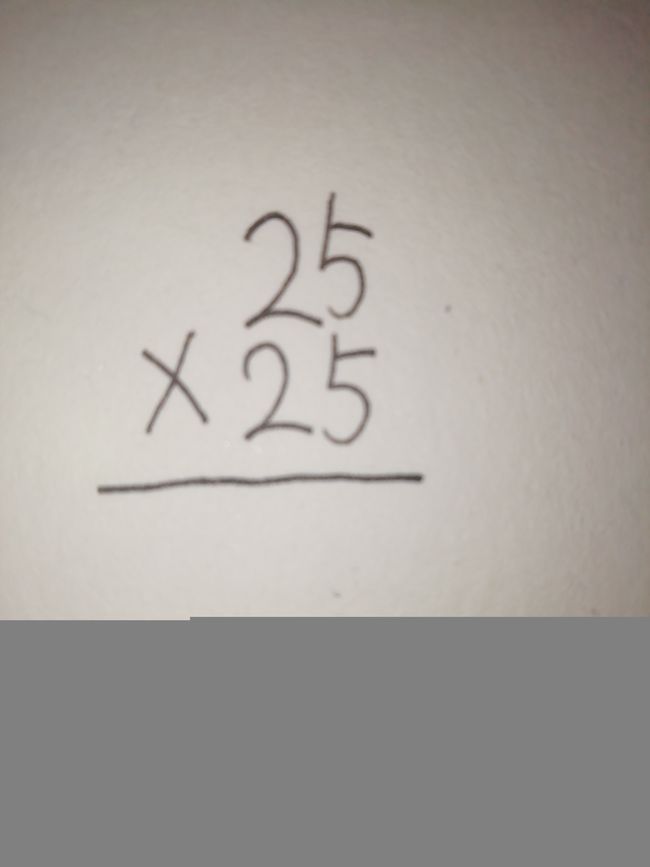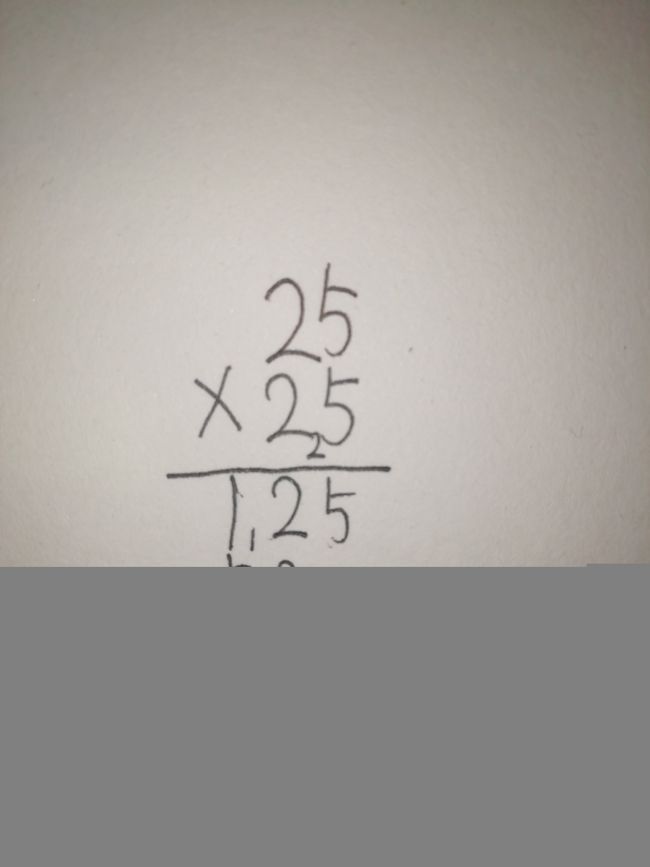1到6年级,也就是我们所说的小学,在这个阶段,学了非常多的数学知识,今天我就来做一个总结,如果要你把小学数学所学的知识分成几类,那么你会怎么分?我们的分类范围就在我们小学所学的东西,还要做到不重不漏,当然,如果分类标准不同,分出的类别也就不一样,现在我把小学数学分成了三大板,就是算数、几何、统计与概率,我们做到了不重不漏,所以,我们今天就来讨论一下小学数学这三大板块。
算术:
现在所说的算数,不是运算,不是加减乘除,不是让你计算一道题,而是数字,下面是我做的算术的综合脑图,如下图。
现在就是要把数字分类,最后我们把数字分成了三大类,第一大类是自然数,第二大类是小数,第三大类是分数,第四大类是负数,(我现在是六上的同学,六下我们会学到负数,负数是我写脑图后期才开始挑战的,所以脑图上没有)现在由我挨个来给大家讲解。
自然数是什么?我们如何定义自然数呢?自然数其实就是整数,就是我们生活中经常说到的12345…,但是自然数是怎么诞生的呢?一个数系是不可能凭空出现,他肯定在生活中有一些缺少的东西,然后才开始发明,那么自然数是如何被发明出来的呢?比如这里有一个苹果,你该如何表示一个苹果,这时候就有了分歧,而祖先就发明了整数,就是表示一个整的东西的数系,自然数也可以运用到我们生活的测量中,比如测量一件物体的长度,还有非常多的例子。最后慢慢演变就成了现在的自然数。而我们还可以把这些自然数分成好几类,如果要分类的话,就得有分类标准,还要有分类范围,我们已经确定了分类范围,就是自然数,而分类标准可以有很多,你有不同的分类标准,就有不同分的类,现在我们来看第一种分类。
奇数与偶数:
我们可以把自然数分别除以二,那么你会得到两种情况,第一种就是余一,第二种就是可以被二整除,然后我们随之而然的就分成了两类,第一种是奇数,就是自然数除以二余下来一的数字,第二种是偶数,就是自然数除以二被整除的数字,我们就分成两类了。
但是……,
你仔细想想,我们有没有做到不重不漏呢?好像没有做到,1和0,他们怎么分类呢?令它可以被二整除,因为0÷2=0,所以林我们把它归到整数类,1不可以被二整除,换一种说法就是,一不是二的倍数,所以呢,我们把1归到奇数类。
但是……,
刚才说的都是特例,我们可不可以用字母来表示奇数和偶数呢?我们如何用字母来表示偶数?我们知道偶数,它可以被二整除也就是二的倍数,所以呢,我们可以用2n来表示,嗯,是随便的一个数字,如果它是奇数的话,乘一个二就是一个偶数,如果是一个偶数的话,乘一个二还是个偶数,所以我们用2n来表示一个偶数,那么奇数呢?你看一个偶数,随便加一个一,还有减去一个一,就是一个奇数,每一个奇数相隔一个数都是还是奇数,所以我们可以用2n-1,来表示一个奇数,当然你用2n+1也可以。这就是奇数和偶数。
因数与倍数:
范围还是自然数,但是我们要把零排除在外,因为零除以任何数还是零,那我们如何定义因数与倍数呢?举一个特例,比如说15÷5=3,那么在这个算式中,我们可以得出,15是3和5的倍数,5和3是15的因数,也就是说,只要任何一个数,他可以整除另一个数时,那么,那么那个数,就是除数还有商的倍数,那么商还有除数,就是被除数的因数,这就是倍数和因数的定义。
但是……,
我们怎么用字母表示呢?比如a÷b=c,那么a就是b和c的倍数,B和c就是a的因数,还有,1可以成为任何数的因数,因为所有数(零除外)除以一都等于那个数本身,所以一是任何数(除零外)的因数。
质数与合数
范围还是自然数,但是我们排除掉1和0,至于为什么要排除1和0呢?我们先继续往下看。
质数与合数,其实和因数有关,那我们怎么定义质数与合数呢?你看,一个数(我们说的所有数都不包括0和1)它的因数除了一和它本身外,有没有其他的因数,如果没有的话,它就是质数,如果有的话,就是合数,我举一个特例,比如三,他除了因数1和3外,没有其他的因数,所以三就是质数,比如四,他除了因数1和4外,他还有因数二,所以四就是合数。
我把自然数分成了这些类,当然你可能会有其他的分类标准,那么分出的类也就不一样,欢迎在下方留言,说说你的分类。
运算
现在我们已经清楚了,自然数的分类,自然数既然是数字,那么它就可以计算,我们可以把自然数进行加减乘除。加,我可以举一个例子,比如4+5,这也是一个自然数的加法运算,那它的含义是什么??也就是集合四家集合五,我们可以用另一种方法来解释,这个方法有了一个基准,就是一,四就是四个一,五就是五个一,四个一加上五个一,那么就是九个一,所以4+5就等于9,那我们如何用字母来表示呢?也就是a+b。减,比如5-4,这是一个自然数的减法运算,那它的含义是什么?就是一个大集合,在这个大集合中拿走一个小集合,还剩下一个小集合,我们还可以用一来解释,实际上是一个基准,也就是五个一减去四个一,最后还剩下多少个一?也就是一个一,那么5-4就是1,那我们该如何用字母表示?也就是A-b,但是还有一个前提,A大于b,在低段年级,这个代数式才成立。而且加减还是互逆的,比如5+4=9,那么9-4就等于五,9-5就等于四,所以加减法,它们之间是有联系的,也就是互逆关系。那么接下来就是乘除法。乘,比如4×5,这个算式的含义是什么呢?其实它有三种含义,第一种含义是几个几,那么4×5,就是四个五,或者五个四,第二种含义就是几个几相加,那么4×5,就是四个五相加,或者是五个四相加,第三个含义就是倍数,四的五倍,但是在不同的情况下,就是用于不同的含义,比如在一到实际应用的题中,你要随机应变,不要总想着一个含义,那么根据这些含义,我们就可以得出,4×5=20,我们可不可以用一个简单的式子,来解决这道题呢,有,那么我们怎么用竖式来表示这个乘法算式呢?比如25×25,其实我们可以把这个25×25分解一下,就变成了5×5+20×5+20×5+20×20,我们可以这样子写。
然后我们一步一步的计算,首先5×5,等于25,2×5(2在十位上),然后2×5(2在十位上),最后2×2(两个2都在十位上),那么整个过程的图就如下。
但是我们得到的两个数字,就放在那吗?那两个数字就是这道题的答案吗?不对,我们要把两个数字加起来,最后等于625,过程如下。
那我们该如何用代数来表示呢?,也就是a×b,但是在我们写的时候,一般都会把乘号给省略了,那么就是AB了。现在就是除,举一个例,比如6÷2,这个算式的含义是什么呢?其实有两种涵义,第一种含义是平均分,就是把六平均分成两份,其中的一份是多少,第二种含义就是包含除,也就是六里包含着几个二,那么我们根据这两种含义,最后就可以得出,6÷2=3,那么除法,我们怎么用竖式来表示?我们先列出来竖式,也就是如下图。
那我们该如何计算?七不能整除三,所以首先要看7内三最大的倍数,那就是六,那几乘3等于6呢?就是2,然后我们把2写到7上面横杠的正上方,余下来1,那么十位上的一加上个位上的二,就是十二,那12以内三最大的倍数是多少?就是12,那么几乘3等于12?就是4,那么把四写到二上面横杠的正上方,那么最后的答案就是24,这也就是除法的竖式,如下图。
所以你以后就可以用除法竖式来解决除的算式了。那么如何用代数来表示呢?也就是a÷b,但是还得有一个前提,A大于b,这样在低段年级的孩子才适用。这就是自然数与自然数之间的运算。
在小学阶段,自然数还可以跟小数分数进行运算。
解方程
自然数也可以融入到我们的方程里,比如ax=b等等等。
实际应用
自然数也可以融入到我们的生活中,也就是实际应用,比如一根铅笔,它的价钱我们就可以用自然数来表示,自然数还可以参与测量,还有表达一个物体的数量,还可以用来解决问题,所以自然数他还有实际应用。
好了,这就是小学阶段,我们学的自然数,我们有可能到初中,高中大学就会对自然数有一个全新的认知,那有谁知道呢?
好,那么这就是自然数了,接下来我们来看一下小数。
小数是什么?我们先要认识一下小数,小数要有一个小数点,后面就是小数位了,第一位是十分位,第二位是百分位,第三位是千分位,第四位是万分位…,比如0.36,它的意义就是36个0.01,也就是摆一平均分成100份,其中的36份就是0.36,所以每个小数位就是一个基准,十分位就是0.1,百分位就是0.01。
我们已经认识了小数,那我们该如何用字母来表示呢?我们可以用一个a.b(b不等0)来表示,因为字母,它可以代表任何的一个数字,那么字母就具有普遍性,所以我们用a.b来表示一个小数。
好,那我们已经认识了小数,我们下一步要做什么呢?就是要把小数分类。
有限小数与无限小数
我们可以把小数有一类分成有限小数,有限小数也是我们生活中常见的一种小数,有限小数有固定的值,它也可以用分数表示,比如0.6,0.74,1.95,都是有限小数,那我们用字母表示就是a.b。
接下来一类就是无限小数,无限小数,顾名思义,就是这个小数是无限的,所以小数又多了一个循环节,比如我有一个0.3循环,也就是0.333…,这个循环节就是一个点,加在第一个三上,那么就代表这个小数是无限循环的,无限小数这个类,还分为无限循环小数,还分为无限不循环小数,它们有什么区别呢?无限循环小数,这个小数是无限的,而且这个小数它是循环的,但是无限不循环小数,他也是无限,但它不循环,也就是在小数点,后面有无数个数位,无限不循环小数其实也有,比如我们常说的兀、根号二(我没有找到那个符号,所以就写出来),他们就属于无限不循环小数,无限不循环,小数还被称为无理数,因为他们没个道理,他们是无限的,还没有一个规律。
运算
小数既然是数字,那么他就可以运算,可以参与四则运算,进行加减乘除,现在我就来讲一下。加法,比如3.4+5.3,这个小数加法算式我们该如何计算呢?你看,我们用自然数加法的内涵来解释这个小数算式的,完全解释不通,因为3.4个5.3相加,5.3个3.4相加,所以我们得用另一种方法,也就是这样,你把3.4变成34,也就是把3.4乘了一个10,同时把5.3也乘一个10,那么这个小数加法算式,就变成了34+53,整数的加法,我们已经会了,那34+53就是87,但是这就是3.4+5.3的答案吗?不是因为我们把每个数字都乘了一个十,两个数字,一共乘的是100,(因为10x10),那么我们就要把87再除一个100,小数点往左移动两位,那么最后得到的答案就是0.87,我们可以用这样的方法来求出一个小数加法的问题,其实这其实这个方法可以在竖式上来表达,还拿3.4和5.3举例子,出来的竖式也就是这个样子的,
签名你可以当成一个整数的乘法算式来算,最后你还得看你一共乘了多少?最后一除,在这个过程中,我们发现了一条规律,在你到最后除你乘了多少的那个部分,你的这个小数乘法算式,小数位有几位,那么最后的得出来的结果就往左移几位,因为你每往右移一格就是乘了一个十,所以这个办法是成立的,那么最后得到的结果就是18.02,如下图。
还剩下一个除法,这个我就不细讲了,因为你列出来除法算式以后,把小数变成整数,然后继续计算,最后记得把结果改正,就可以了,那么加减乘除算式如下图(直接用字母表示)
小数的加减乘除的含义跟自然数一样,所以我就不细说了,小数可以跟小数运算,那么也可以跟自然数分数运算,等我们再大一点,还可以跟复数,其他数字运算。
解方程
小数也可以参与到解方程,比如3.8a=42,等等。
实际应用
在生活中,小数还是非常常见,比如一根棒棒糖就0.5元,小数也可以参与到测量中,还有表达一个物体的重量,…还有好多。
好了,这就是小学阶段,我们学的小数,我们有可能到初中,高中大学就会对小数有一个全新的认知,那有谁知道呢?
这就是小数了,我们现在来看一下分数。
分数是什么?如果我们要研究这个数系的话,先要认识一下分数,分数他有分母也有分子,最重要的还有一个分号,也就是下面的这个样子,下面的这个数字也就是一个分数。
好,那分数的含义是什么呢?每个数字都有它的含义啊!我们来举一个特别经典的一个例子,今天小明过生日,爸爸妈妈为她买了一个蛋糕,到了晚上他们要吃蛋糕了,他们该怎么分这个蛋糕呢?我们都知道,要不然这个蛋糕平均分成三份,这样的话,每个人吃到的蛋糕才一样,那我们该如何表达?每个人吃到的蛋糕呢?其实蛋糕就是一个整体,也就是单位一,然后我们把这个整体平均分成三份,那么其中的一份就占这个整体的1/3,那其中两份就占这个整体的2/3那么再来一个蛋糕,其中的四份就占一个蛋糕,一个整体的4/3。我现在再举一例子,比如3/4,我们是把它理解成把整体一平均分成四份,其中的三份就占原来的整体的3/4,但是它还有另一种含义,就是整体一平均分成四份,其中的一份就占这个整体的1/4,现在有三个这个整体,那么一共有多少份呢?,也就是有三个这个单位1/4,最后还是3/4,现在我们就理解丰富的含义了,其中的一个意义就是部分与整体的关系,然还有另一含义,就是一个具体的量,有1/3也可以表达一个量,所以分数有两种含义。而我后来发现,1/4,也就是1÷4的结果,所以分数还和除法有密不可分的关系,在1÷4这个算式中,一也就是我们最后得到的分数结果的分子,四也就是我们最有得到的分数的结果的分母。
分类
现在就是要把分数给分类了,分类的范围就是分数,按照分类标准分出来的类还要做到不重不漏。
最后我把分数分成了假分数,真分数,带分数,还有百分数。
你可能要问了,为什么分数还有真假呢?还有带分数呢?其实,真分数就是一个分数,它的分子小于它的分母,没有满足一个单尾一,比如1/3,1/4,4/5,这就是真分数,那我们怎么用字母来表示呢?就是b/a,但是它也是有限制,就是b小于a,A不等于零,这样这个代数才是一个真分数,那么假,分数是什么呢?就是一个分数的分子,大于它的分母,或者等于它的分母,这样的话,这个分数就是一个假分数,那我们怎么用字母表示呢?就是b/a,A等于b,b大于a,a不等于零,这样的话才成立。那么带分数是什么呢?其实带分数也是假分数,他有两个部分构成,一个是整数部分,另一个是真分数部分,比如这个假分数,5/4,那么带分数就是11/4,我们把它读成一又1/4,因为5/4满一了,那么4/4,我们就用一来表示,那么我们用字母表示就是,AC /B,前提是a和b不等于零,还有c小于b。百分数,就是一种特殊的分数,它的分母永远是100,不用约分,但是通常我们把那个百,用另种符号来表示,百分号,就是这个%,分子就在这个百分号前面,那么我们用字母表示就是a%,那么这就是分数的分类了。
那么分类完成,下一步就是运算了。
运算
分数的加法也是分为两类,第一类是同分母的分数加法,第二类是异分母的分数加法,同分母的分数加法其实就是把分子相加,比如2/3+1/3,意义就是两个1/3,加上一个1/3,最后就等于三个1/3。异分母的分数加法,比如2/6+1/3,你可以把2/6约分成1/3,这样就变成了同分母的加法,有时也可以通分,比如5/6加2/3,这个5/6就无法约分,那么我们就要通分2/3,分子和分母同时乘以一个数,最后变成这两个分数的分母的最小公倍数,那么2/3,2和3都要乘一个,就是4/6,4/6+5/6,就等于9/6,最后再约分,就是3/2。如果是一个整数和分数进行加减的话,你就可以把这个整数化成一个分数,然后继续和分数进行加减,这就是分数的加法。
接下来学习的就是分数的减法,分子减法以分为两类异分母的分数减法和同分母的分数减法,同分母的分数减法,比如说2/3-1/3,意义就是两个1/3减去一个1/3,最后,也就等于一个1/3,异分母的分数减法,也就是把分数通分或者约分,这就是从分母的分数减法。
分数乘法也可以分为两类,一类就是分数乘整数,另类就是分数乘分数。
分数乘整数,比如1/3×2,他的意义就是两个1/3,有两个一个1/3,也可以画图表示,如下图。
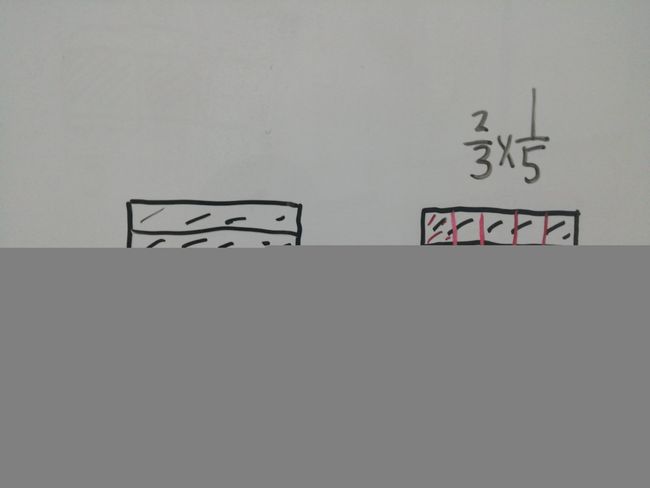
接下来我们要知道的就是分数乘分数,如果你不画图,表示团是特别难理解的,所以我画了一个图,如下图。
这道题的意义,也就是有两个在2/3的1/5,最后也就是2/15了,所以分数乘分数没有必要分同分母和异分母的,我们也得到了一个法则,分母乘分母,分子乘分子,这就是分数乘法的法则。
分数除法,我们也可以分成两类来讲,第一类是分数与整数,第二类是分数与分数。
分数与整数,比如1/3÷3,这道题的结果是什么呢?现在用我们的自然数的除法含义,就非常难解释,平均分还有包含图都不适用,最后经过我们的讨论,发现除以三就等于乘以1/3,其实是1/3,乘了三的倒数,三我们也可以用分数来表示,就是3/1,那么乘以3/1的倒数就是乘以1/3,最后的结果就是1/9了,所以分数除以整数,就是等于分数乘以整数的倒数,那如果是整数除以分数呢?就是整数乘以分数的倒数。
分数与分数,我来举一个例子,比如3/4除以1/2,他的结果是多少呢?我来画一个图,你就明白了。
这张图也印证了刚才我们所说的乘以倒数的方法,那么3/4÷1/2,等于3/4×1/2的倒数,也就是3/4×2,我们也就会了。这就是分数的除法。
分数也可以参与到我们的实际应用,还有解方程,这里我就不细讲了。
这就是分数了,我们现在来看一下负数。
负数是一个非常神奇的数系,负数是小于零的数字,而整数就是大于零的自然数,负数我们还没有学过,但是我已经对他有了一个非常大的兴趣,所以今天我们就来谈一下负数。
负数的诞生
一个数系他是不可能凭空出现的,肯定是在实际中遇到什么问题,然后来解决它,最后就有了一个新的数系,负数也一样,那么负数,他是如何诞生的呢?
负数肯定是根据我们的生活需要才诞生,比如你去东北,那里的温度是多少呢?温度已经在0度以下,那么我们该如何表示这个温度呢?比如零下10度,我们就可以用-10。C来表示(句号在上面),表示温度的那个数字,就是一个负数。
这就是负数的诞生,在我们的生活中,时时刻刻都有负数的存在,我们同样也需要负数。那我们该如何确定一个数字?他是不是负数呢?其实1的正确的表达方法是+1,但是我们经常都把那个加号给省略,而负数呢?它的数字前面有一个减号(-),所以如果你要确定一个数字,他是不是负数的话,只看它前面有没有减号就可以了。
负数该如何比大小?
接下来我们进入此篇论文的第二部分,复数该如何比大小?
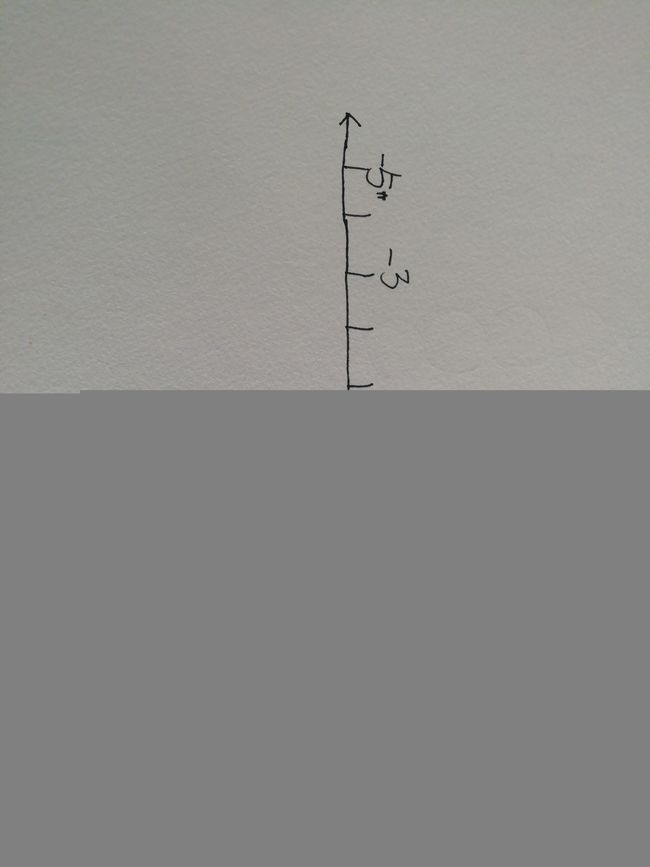
现在我来举一个特例,-3和-5,他们两个之间谁更大?如果是3和5,我们知道是5更大,我们可以画图来解释。
我们知道,在数轴上,一个数字,越靠右边,它就越大,那我们先看3和5,5比3靠右,所以呢,5比3大,那么我们再来看-5、-3,是谁更靠右呢?是-3更靠右,所以-3比-5大。
但是我刚才举的都是特例,不能代表所有的负数,那我给你一个-a,还有-b,哪个更大呢?
当我们在比较-3还有-5谁更大的时候,你可能总结出来了一条规律,整数比大小,谁数字大谁就大。负数比大小,谁的数字越小,谁就越大,谁的数字越大,谁就越小,因为数字越小的负数,他就更接近于零,数字越大的负数,就更远离零,所以在我们比较-a还有-b大小的时候,A和b比较,谁更大,谁就越小。
运算
在负数的运算中,我分了两类,第一类是负数与负数,也就是负数与负数运算,第二类是负数与整数,也就是负数与整数运算,所以我会分两大部分来给大家讲加法。
加法一:(负数与负数)
我来举一个特例,比如-2+(-3),这个算式等于等于多少?这个问题我们可以用画图来解释,也就是画数轴,该怎么画数轴,我现在再举一个特例来对比一下,2+3。
上面的那个数轴是来表示2+3,零为开始往右跳,每一格是1,第一次跳两格,跳到二的位置,第二次再往后跳三格,跳了三,一共跳了五格(2+3格),这是整数的加法,那复数的加法呢?也就是零为开始,往左跳,每隔是-1,第一次跳两格,跳到-2的位置,第二次再往后跳三格,跳了-3,一共跳了多少?这时候你数下格数,就知道我们一共跳了五格,而五格在这个数轴中就是-5,你会发现好像就是负号后面的数字相加了,那我再举一个例子,比如-4+-6,也就是-(4+6),最后得到的答案也就是-10。
而上面说的也都是特例,不能代表所有的负数,所以-a+-b等于多少呢?按照我们刚才得到的结论,也就是-(a+b),这个式子可以解决任何的加法,所以负数的加法,我们已经知道该如何解决了。
加法二:(负数与整数)
我们还是举一个例子来解答,比如-2+3,这个算式等于几?这就是一个负数与整数的加法算式,而像这种类型的算式,我可以举一个实际例子来解答。
小明在家,到了周末他要去小刚家玩(小明在a地,小刚在b地),小刚家在小明家出门正右方(正东方,)小明出门后去正左方(正西方)二公里的便利店买了些水果要带去小刚家,买完水果后,往小刚家方向走了三公里,这时到了小刚家,请问小刚家离小明家的位置是多少公里?(故事可能不合理,凑合凑合看)故事图如下。
如果小明家所在的位置是零的话,要往右走,那么便利店的位置就在-2(公里),在王小刚家方向走3公里,这个过程我们就可以列出一个算式,-2+3,那么最后等于几?我们可以结合这个故事来求出,先是两公里,再走三公里,三公里的,其中两公里就抵消了,最后只剩下一公里,那么-2+3就是等于1。
在我们求出这个算式的时候,你可能会觉得,整数的一,和负数的负一,它们的值是一样,我用图来表示。
所以负一还有一的量,很有可能是一样,但是我现在还不能确定,因为我们还没有学负数,我现在是在挑战,所以我们可以暂且这么认为,所以你碰到一个负数加法算式,就可以运用这样的方法来计算,最终得到他的结果。
这就是加法部分的复数的运算,我们现在就要进入减法的负数运算了!
减法一:(负数与负数,减数大于被减数)
举一个特例,举一个特例,-3-(-2)等于多少?我们可以用单位来解释,我们把负一看成一个单位,那么负三就有三个负一这个单位,负二就有两个负一这个单位,那-3--2,就是3个-1剪去2个负一,那最后只剩下一个负一了,所以答案就是-1。
这种题型的问题非常简单,我们直接用上面的方法来解释就可以了。
但是这种类型的题还可以用另一种方法来解释,其实每一个负数他应该都加一个括号的,那么这个算式列出来也就是这个样子。
负二还有另种方式来表达,就是0-2,那我们可以把刚才的算式转化成如下图
这时候如果我们要继续进行运算的话,就要把括号给去了,在我们三年级的时候就讨论了,该如何去括号,括号中如果是减号的话,把括号去了,就把减号变成加号,那么这个算式也就变成了这个样子。
现在我们可以继续往下进行运算,-3-0,等于没有减任何东西,所以最后就变成了-3+2,-3+2,像这种算式,我们已经在前面的加法中讨论过,该如何计算了,那么最后的答案就是负一,跟我们刚才得到结果一样,不过这个办法更麻烦了一点。
而我们说的也都是特例,不能代表所有的负数,我现在就列一个代数,用我的第二种方法来解释,那么最后就是如下图。
减法二:(负数与整数,整数是被减数)
来举一个特例,比如3-(-2),这道题我们该如何算呢?其实我们可以用我们刚才的方,也就是把负二表示成0-2,那我们看看该如何计算。如下图。
我们现在就是去括号,那把括号去了,括号中的减法已经变成加法,如下图。
我们现在继续计算,如下图。
好,那么这道算式我们就会求了,最后的结果是五。
但是我们举的仍然是特例,我们必须得用代数来表示,才能证明它的普遍性,如下图。
那么这一类的题我们就会解决了。
减法三:(负数与整数,负数是被减数)
举一个特例,比如-2-3,前面我们已经讨论过,副号其实就是减号,减号也可以成为负号,就像负二,那么在这个例子中,有两个减号,一个是我们的负二的负号,另一个是减号,但是减号我们可不可以把它看成负号呢?如果把减号看成负号的,那么减三就是负三,那么在这道题中就有两个集合,一个是负二,一个负三,现在就差的是他们两个相加,-2+-3我们已经会求了,就是-5。
那我们现在用代数来表示,就是这个样子。
乘法一:(负数与负数)
你有没有听过负负得正?他就向我们所学的语文,一个否定句,有两个否定词,那就是一个肯定句了,那么负数的负负得正是什么意思?就是负数乘以负数,最后得到的答案是一个整数,我不知道这是人类验证的,还是规定,那我们来举一个特例,比如-3×-2,负负得正,把负号减了,就是三乘二,那么最后的结果就是六。
乘法二:(负数与整数)
举一个特例,比如-3×2,那么它的结果是多少呢?这道题的含义,我们可以用自然数的含义来解释,两个负三相加,加法红们已经会了,就是负六,还有另一种含义,就是负三的2倍,还是两个负三,最后的结果也是负六,那么你会总结出一条规律,就是负数上的数字乘以你要乘的整数,前面再加一个负号就可以了。这就是我认为的复数的乘法。
除法一:(负数与整数)
复数的除法,我来举一个特例,-3÷2,我们可以利用分数的除法来计算,那么就是-3×2的倒数,也就是-3×2,-3×1/2,我有一个猜想,就是-3/2,因为我们还没有学,但是我感觉应该是这样子的。
除法二:(负数与负数)
举一个特例,比如-3÷-2,这个算式,我们该如何求呢?我们还可以利用刚才的方法,把除以负二等于乘以-1/2,负二的倒数应该就是-1/2吧,那么也就是-3×-1/2,但是我们刚才说了,负负得正,是复数乘法的法则,那么应该就是3/2了。这就是我认为的复数的除法。
好,这四个小部分我们讲完了,算数还剩下未来,你认为有什么呢?
接下来,就是第二大板块——
几何
这是我写的几何的综合脑图,如下图。
一维~线
首先我们来确定什么是线,线是直的,线具体分为线段、直线、射线,那么这三条线又是什么概念呢?直线,它没有一个准确的端点,它可以两边无限延长的的,这就是直线的性质。射线,它是有一个端点,然后另一条边可以无限地延长,我们生活中有很多射线,比如在灯光秀中,你看见灯光,它其实就是一条射线,红外线,绿外线,手电筒,也是射线,这就是射线的性质。线段,它有两个端点,这条线是有限制,不能无限延长。这就是三条性质不一的线。
假如你的面前有一条线,你会怎么来表达这条线的长度呢?在古代,还没有,现在西方统一标准的基准单位,那他们怎么表达这条线的长度呢?所以我们就遇到了问题,一条线,我们表达会不统一。其实在古代,他们也有表示的方法,寸、拃、丈,这三个单位就是他们测量一条线的基准,但是他们是怎么得来的呢?其实原本只有一个计量单位,在实际使用中,肯定会有一些问题,就是一条线的长度不满足这个单位,那么他们就得发明单位更小的基准,所以就有了进置,比如十拃就是一仗,所以每一个测量基准中都是有进置的。那么在现代,我们用什么基准呢?在西方,他们用了厘米毫米、米、分米,他们的国家相对于其他国家来说都要强盛,所以他们的计量方法就成了国际的标准,所以现代的已经统一了基准,就是厘米、毫米…,现在我们采用的是十进制,十毫米等于一厘米,十厘米等于一分米,十分米等于一米。
那我们现在已经有了一个统一的测量基准,那么如何测量呢?第一肯定是需要确定一条线的起点,就是端点,然后我们来测量这条线,看这条线有几个这样的基准,这样我就可以得知一条线的长度。
这就是一维~线的长度。
二维~平面图形
平面图形的定义是什么?就是一个部分,如果在这个平面内,他就是一个平面图形,比如长方形,他有长和宽,在这个平面内,他就是一个平面图形。
那么你学过哪些平面图形?
有长方形,正方形,在我们学这些图形的时候,有两个重要的部分,就是周长和面积,现在先来看看正方形和长方形的周长面积。长方形的周长,其实就是它的四条边的长度加起来,就是这个平面内它的边缘的长度就是这个图形的周长,那么我们只要把长方形它的长和宽的长度量出来,加起来就是正长方形的周长,正方形,那我们量出它的边长,然后加起来就是正方形的周长了。那我们现在来看它们的面积。正方形和长方形面积,我们可以用两种方法来解释,就是拉伸系数和平移变换,现在我们有一个小正方形,然后我们把这个图形拉伸,我们是把这个正方形拉伸了,那我们先把它横向拉伸a倍,再向纵向拉伸b倍,那么他一共拉伸了多少倍?就是a乘b倍,也就是运用了乘法。平移变化,就是一个单位小正方形,用它来摆成了一个长方形,那我们怎么算这个长方形的面积?就是看他这个长方形,一共有几个这个单位小正方形?,一个一个数,用的就是加法,但是拉伸系数用的就是乘法,这就是求长方形和正方形的面积方法。
接下来就是平行四边形梯形三角形的面积,其实它们的面积运用的是割补方法,比如一个直角三角形,你可以再补一个跟它相同的直角三角形,那么就可以拼成一个长方形或者正方形,长方形面积就是长乘宽,再除以二就是这个三角形的面积,那么在这个三角形中,长方形的长和宽,就是三角形的底和高,所以三角形面积就是底乘高除以二。平行四边形,沿着平行四边形高切意切一刀,然后就是两个梯形,这两个梯形的斜边是一样的,就可以把它拼成一个长方形,长乘宽,长和宽在这个平行四边形中就是底和高,所以平行四边形面积就是底乘高。梯形,我们找一个一般梯形,沿着它相对的对角线切一刀,就是两个三角形,三角形的面积,我们已经知道该如何求了,底乘高除以二,这两个三角形的底和高,就是梯形的上底和下底,三角形的高就是梯形的高,所以梯形面积就是(下底加上底)乘高除以二,我们运用勾股求出这些图形的面积。
然后我们在六上学习了圆的面积,我们把圆分割成近似的三角形,然后把分割成近似三角形后的圆展开,就是两个部分,这时我突然发现,可以买那两个部分,拼成一个长方形,长方形的面积,我们已经会求了,就是长乘宽,那么这个长方形的长和宽在这个圆中是什么呢?长就是周长的一半,宽就是圆的半径,长是兀r,宽就是r,那么圆的面积就是兀r2,但是这个方法有什么不好的地方呢?就是我们无法做到把这个圆分割成三角形,只能分割成近似的三角形,但是如果我们用大脑使用极限思想,想象把这个圆分割成无数份,那么分割出来的图形就是三角形,它的底边也就是直的,那么这个方法就成立了。
三维~立体图形
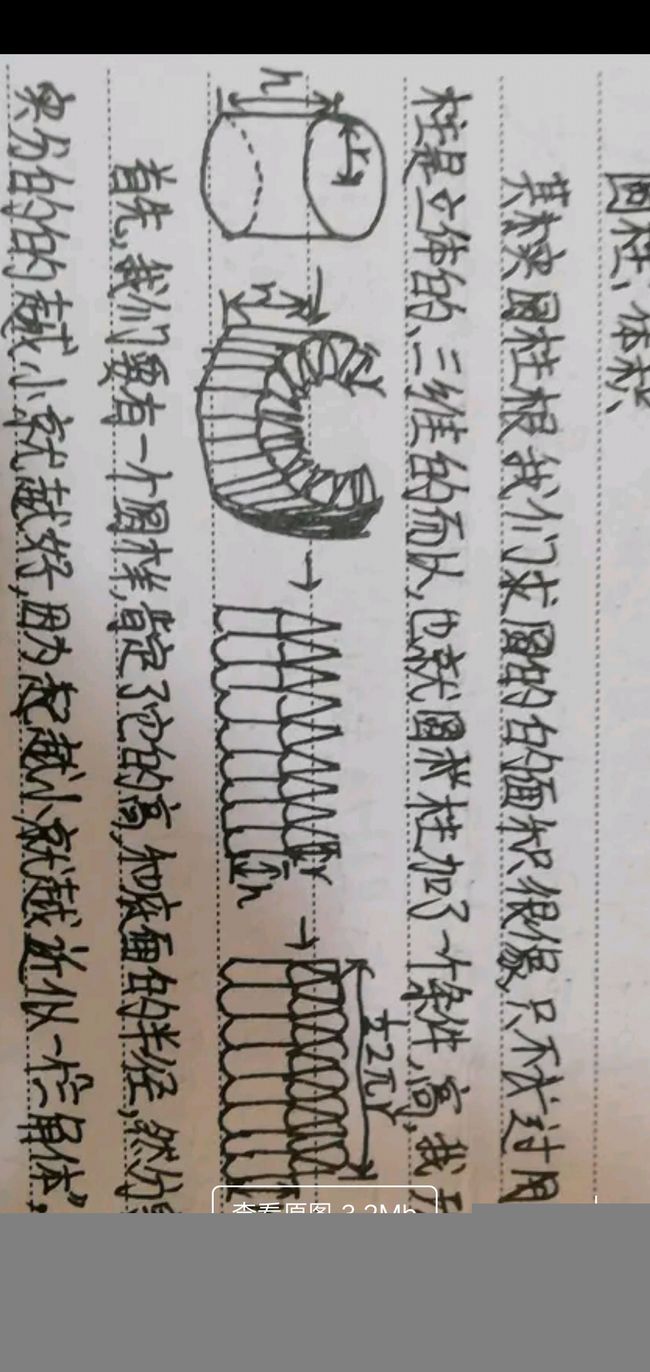
立体图形就像现实生活中的,是个三维世界,我们就像一个立体图形,不过是一个不规则的,立体图形最重要的两个点就是体积和表面积,一个长方体表面积就是它,每个面的面积加起来,就是他的表面积,现在我们来算一下圆锥的表面积,我的方法是把圆柱展开,展开之后也就是两个大小同样的圆,和一个长方形,现在我们设圆的半径是r,那圆的面积就是r2兀,(r的平方乘以兀),有两个相同的圆,就是2×r2兀,现在如果我们要算长方形的面积话,需要长和宽,宽在这个圆柱中就是高h,那么长是什么呢?你会发现长就是围成底面的周长,所以长就是圆的周长,圆的半径是r,周长就是2兀r,长方形的长和宽有了,就知道它的面积该怎么算了,面积也就是2兀r×h,那圆柱的表面积也就是2兀rh+2r2兀,等于说要想知道圆柱的表面积,只用知道半径和高就行了。现在就是圆锥的表面积。我们想象把这个圆锥展开,最后想到圆锥展开以后是一个扇形,和一个圆形,圆形也就是圆锥的底面。我们算出圆的面积和扇形的面积,那我们现在要知道弧AB的长度了,其实弧就是圆的周长,因为是弧围成了底面,也就是边缘,半径就是R,这个扇形的半径还被称作为母线,那扇形的面积就是,那么扇形的面积就是1/22兀r×R,那么圆锥的表面积就是1/22兀r×R+r2兀。
接下来就是体积,我们可以用拉伸系数和单位小木块来得知这个长方体的体积,比如这里有一个单位基准小正方体,然后把这个正方体三维拉伸,拉伸a倍,拉伸b倍,拉伸c倍,那他一共拉伸了多少倍?就是a×b×c,我们算它的体积,运用到了乘法。另一种就是单位基准小正方体,来铺满这个长方体,看有多少个这个单位基准小正方体,运用到了加法,这就是这个长方体的体积,正方体同理。
接下来就是圆锥,还有圆柱的体积了。
我这样分割一个圆柱,其实分的越小越好,越小就越近似一个三角体,但是我们是做不到把应援的周长分成三角形的底,我们想象一下,分出来的就是三角体,然后把它展开,把这些三角体拼成一个长方体,我们知道长方体的体积怎么算,就是长乘宽乘高,那么这个长方体的长是多少呢?长方体的宽是多少呢?长方体的长呢?长也是圆的周长的一半,所以是1/22兀r,宽就是图中的半径,r,那么长方体的高是什么呢?,长方体的高就是圆柱的高h,三个条件都有了,那么体积是什么呢?就是长乘宽乘高,也就是1/22兀r×r×h,我们来化解一下,就是1/22兀r×r×h=r兀×r×h=r2兀h,你会发现就是圆柱的底面积乘高,这就是圆柱体积的法则。
然后就是圆锥的体积了,我有一个猜想,就是圆锥的体积和它同底面积等高的圆柱的体积的1/3,所以我们就做了这样的一对圆锥和圆柱,我们就去操场上弄些土,我们先装满圆锥,然后把圆锥上的土倒入圆柱,最后我们倒了三次,差不多就把圆柱倒满了,所以可能圆锥的体积就是和他同底面积等高的圆柱体积的1/3,事实上就是这样,我们只能用物理实验来证明,不能用数学来推理,所以圆锥的体积就是它的底面积乘高乘以1/3。
因为我们学的统计与概率的内容比较少,所以我就不细讲了。
好,那么这就是小学数学所学的三大板块,我们就讲完了,你还有什么疑惑可以写到下方留言区,喜欢这篇文章的话,可以点赞分享哦!拜拜!!!