1.案例说明
通过已知获救数据,预测乘客生存情况
2.查看数据
#读取数据
data = pd.read_csv('train.csv')
#查看数据
data.head()
#数据类型
data.info()
字符串类型变量有Name(文本格式,需从中提取有效信息),Sex(二分类变量),Ticket(票根号,无意义),Cabin(无序分类变量),Embarked(无序分类变量),其余数值型变量为连续变量
3.数据预处理
#定义连续自变量,和连续因变量
cols = data.columns.tolist()
cols.remove('PassengerId')
cols.remove('Survived')
var_c = ['Age','SibSp','Parch','Fare']
var_d = list(set(cols) - set(var_c))
#缺失值处理
data.isnull().sum()/len(data)
其中Age,Cabin,Embarked有缺失值
Age变量缺失率19%,填充中位数
Cabin缺失率较大,根据对数据的理解,填充N表示无船舱
Embarked(登船口岸)为分类变量,缺失量较小,填充众数(出现频率最高的值)
#age属性填充中位数
Age_fillna = data['Age'].median()
data['Age'].fillna(Age_fillna,inplace = True)
#Cabin缺失率较大,根据对数据的理解,填充N表示无船舱
data['Cabin'].fillna('N',inplace = True)
#Embarked(登船口岸)为分类变量,缺失量较小,填充众数(出现频率最高的值)
Embarked_fillna = data['Embarked'].mode()[0]
data['Embarked'].fillna(Embarked_fillna,inplace = True)
#将清洗变量添加入列表
dataclean =[]
dataclean.append({'Age':Age_fillna})
dataclean.append({'Cabin':'U'})
dataclean.append({'Embarked':Embarked_fillna})
利用众数减去中位数的差值距离四分卫距来查找是否有可能存在异常值(高频值)
#各变量小于0.8无高频值
4.修改变量及探索性分析
分类变量
对文本类变量,提取有效信息
Name变量 姓名前的前缀表示乘客的身份,如Braund, Mr. Owen Harris,Mr表示乘客是已婚男士
data['Name'] = data['Name'].str.split(',').str[1].str.split('.').str[0].str.strip()
data['Name'].value_counts()
对提取出来的身份进行分类
title_mapDict = {
"Capt": "Officer",
"Col": "Officer",
"Major": "Officer",
"Jonkheer": "Royalty",
"Don": "Royalty",
"Sir" : "Royalty",
"Dr": "Officer",
"Rev": "Officer",
"the Countess":"Royalty",
"Dona": "Royalty",
"Mme": "Mrs",
"Mlle": "Miss",
"Ms": "Mrs",
"Mr" : "Mr",
"Mrs" : "Mrs",
"Miss" : "Miss",
"Master" : "Master",
"Lady" : "Royalty"
}
data['title'] = data['Name'].map(title_mapDict)
dataclean.append({'name':title_mapDict})
Cabin(船舱号)开头字母表示所在区域,提取该变量
data['Cabin'] = data['Cabin'].str[0]
查看个分类变量分类水平
data['Pclass'].value_counts()
data['Embarked'].value_counts()
data['Cabin'].value_counts()
data['title'].value_counts()
探查分类自变量与因变量相关性
title变量
import seaborn as sns
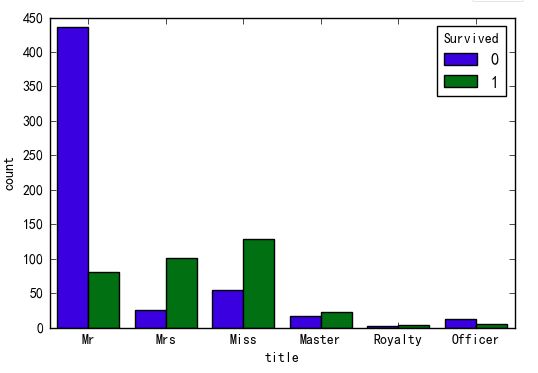
sns.countplot(x='title',hue='Survived',data=data)
卡方检验
from scipy.stats import chi2_contingency
ct_title = pd.crosstab(data.title,data.Survived)
print('p-value:%f'%chi2_contingency(ct_title)[1])
p-value:0.000000
title身份变量与是否存活有显著相关性
Mrs已婚女性,Miss未婚女性,Master有技能的人存活概率更高
Pclass变量
sns.countplot(x='Pclass',hue='Survived',data=data)
ct_Pclass = pd.crosstab(data.Pclass,data.Survived)
print('p-value:%f'%chi2_contingency(ct_Pclass)[1])
p-value:0.000000
Pclass客舱等级变量与是否存活有显著相关性
高等级客舱乘客存活概率更高
Cabin变量
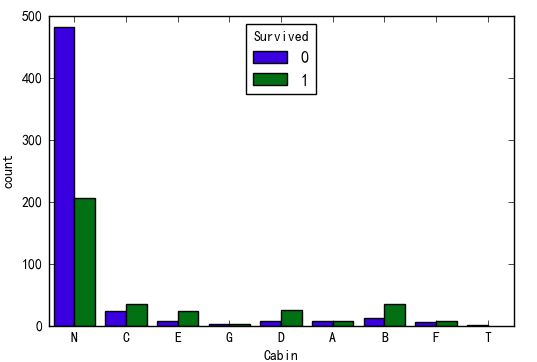
sns.countplot(x='Cabin',hue='Survived',data=data)
ct_Cabin = pd.crosstab(data.Cabin,data.Survived)
print('p-value:%f'%chi2_contingency(ct_Cabin)[1])
p-value:0.000000
Cabin船舱号变量与是否存活有显著相关性
船舱号为N(无船舱号,代表乘客可能居住在底层无船舱)获救几率很低
Embarked变量
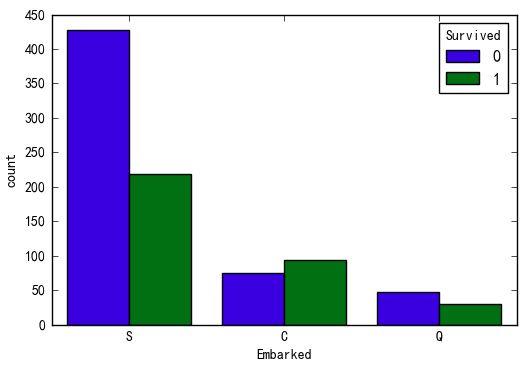
sns.countplot(x='Embarked',hue='Survived',data=data)
ct_Embarked = pd.crosstab(data.Embarked,data.Survived)
print('p-value:%f'%chi2_contingency(ct_Embarked)[1])
p-value:0.000002
Embarked登船口岸变量与是否存活有显著相关性
在C口岸登船的乘客生存几率较高,可能C口岸登船的身份较显贵
Sex变量
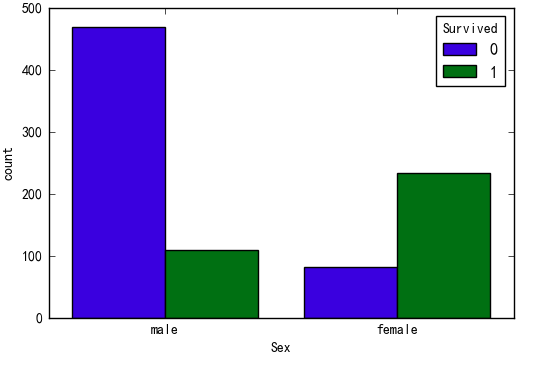
sns.countplot(x='Sex',hue='Survived',data=data)
ct_Sex = pd.crosstab(data.Sex,data.Survived)
print('p-value:%f'%chi2_contingency(ct_Sex)[1])
p-value:0.000000
Sex船舱号变量与是否存活有显著相关性
女性获救几率明显高于男性
连续变量修改
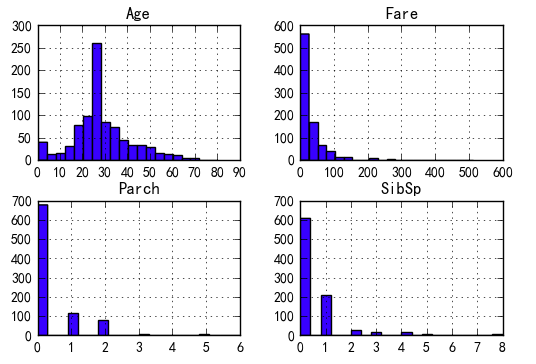
连续变量分布
data[var_c].hist(bins=20)
plt.show()
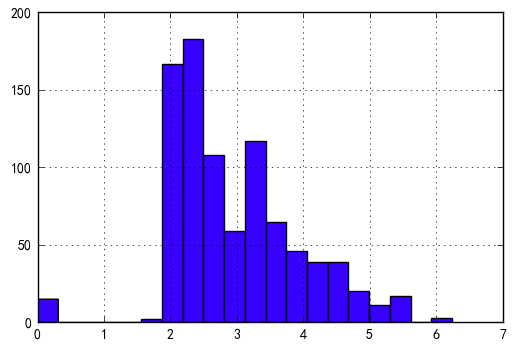
Fare呈偏态分布,正太转化
data['Fare_log'] = np.log1p(data['Fare'])
data['Fare_log'].hist(bins=20)
plt.show()
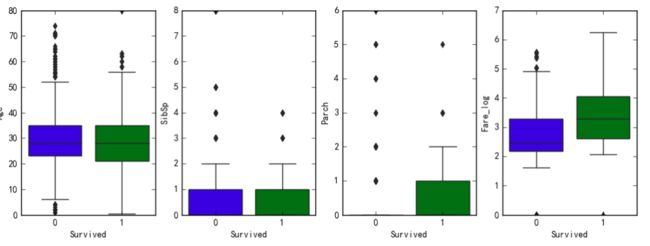
分类变量探索性分析
fig,ax=plt.subplots(ncols=4,figsize=(12,4))
sns.boxplot(x='Survived',y='Age',data=data,ax=ax[0])
sns.boxplot(x='Survived',y='SibSp',data=data,ax=ax[1])
sns.boxplot(x='Survived',y='Parch',data=data,ax=ax[2])
sns.boxplot(x='Survived',y='Fare_log',data=data,ax=ax[3])
双样本t检验
Age变量
age_0 = data['Age'][data['Survived']==0]
age_1 = data['Age'][data['Survived']==1]
#方差齐性检验
stats.levene(age_0,age_1)
#方差不相同
s,p = stats.ttest_ind(age_0,age_1,equal_var=False)
print('p-value:%6.4f'%p)
p-value:0.0583
存活与否的年龄差别不显著
Fare变量
Fare_0 = data['Fare_log'][data['Survived']==0]
Fare_1 = data['Fare_log'][data['Survived']==1]
#方差齐性检验
s,p =stats.levene(Fare_0,Fare_1)
print('p-value:%6.4f'%p)
#方差不相同
s1,p1 = stats.ttest_ind(Fare_0,Fare_1,equal_var=True)
print('p-value:%6.4f'%p1)
p-value:0.0000
存活与票价有显著关系
相关性分析
sns.heatmap(data[var_c].corr(),vmax=1,annot=True)
变量间无高相关性
5.构建模型
重新定义进入模型内变量
var_c =['Age', 'SibSp', 'Parch','Fare_log']
var_d = ['title', 'Pclass', 'Embarked', 'Cabin', 'Sex']
cols_f = []
for col in var_d:
col_f = 'C(%s)'%col
cols_f.append(col_f)
cols_f = cols_f+var_c
将数据拆分成测试集和训练集
from sklearn.model_selection import train_test_split
train,test = train_test_split(data,test_size=0.3, random_state=1234)
训练集和测试集比例7:3
使用向前法筛选变量
定义向前法
def forward_select(data,cols,y):
remaining = cols.copy()
current_score,best_score =float('inf'),float('inf')
selected = []
while remaining:
aiclst = []
for i in remaining:
formula = '%s~%s'%(y,'+'.join(selected+[i]))
aic = glm(formula=formula,data=data,family = sm.families.Binomial(sm.families.links.logit)).fit().aic
aiclst.append((aic,i))
aiclst.sort(reverse=True)
best_new_score,best_i = aiclst.pop()
if current_score > best_new_score:
remaining.remove(best_i)
selected.append(best_i)
current_score = best_new_score
print('aic is %f,coutinuing'%current_score)
else:
print('forward_select over')
break
return(selected)
筛选变量
import warnings
warnings.filterwarnings('ignore')
cols_f_m = forward_select(train,cols_f,'Survived')
筛选后变量:['C(title)', 'C(Pclass)', 'SibSp', 'Age', 'Fare_log', 'Parch']
构建模型
formula = 'Survived~' +'+'.join(cols_f_m)
lg_m1 = glm(formula=formula,data=train,family = sm.families.Binomial(sm.families.links.logit)).fit()
lg_m1.summary()
模型P值小于0.05
6.模型评估
roc
from sklearn.metrics import roc_curve,auc
test_y = test['Survived']
pred_y = lg_m1.predict(test)
fpr, tpr, threshold = roc_curve(test_y, pred_y)
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, color='darkorange',label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC_curve')
plt.legend(loc="lower right")
plt.show()
ROC:0.85 模型效果较好
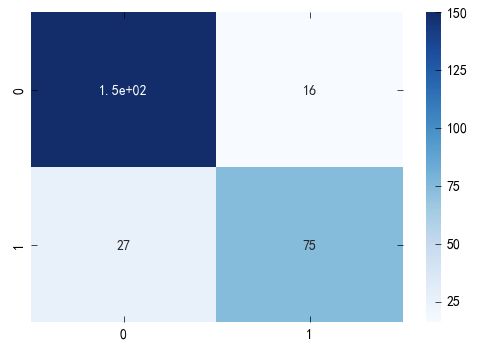
混淆矩阵
#以0.5为阈值
#混淆矩阵图
pred_y_p = pred_y.map(lambda x:1 if x>0.5 else 0)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(test_y, pred_y_p)
sns.heatmap(cm,annot=True,vmax=150,cmap='Blues')
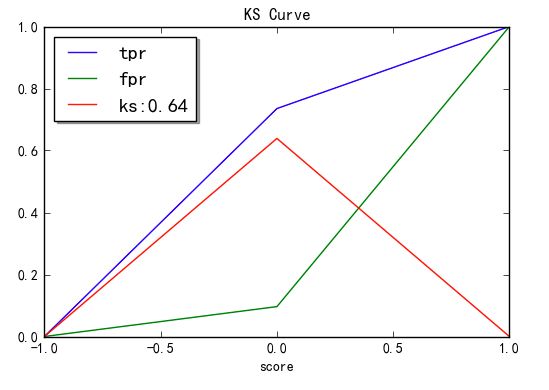
KS值
fig, ax = plt.subplots()
fpr, tpr, threshold = roc_curve(test_y, pred_y_p)
ax.plot(1 - threshold, tpr, label='tpr') # ks曲线要按照预测概率降序排列,所以需要1-threshold镜像
ax.plot(1 - threshold, fpr, label='fpr')
ax.plot(1 - threshold, tpr-fpr,label='ks:%.2f'%np.max(tpr-fpr))
plt.xlabel('score')
plt.title('KS Curve')
plt.figure(figsize=(20,20))
legend = ax.legend(loc='upper left', shadow=True, fontsize='x-large')