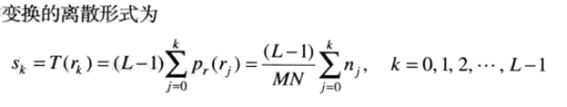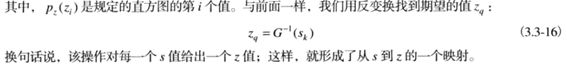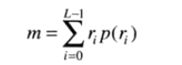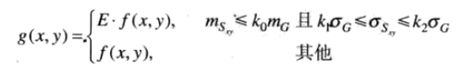第三章 灰度变换与空间滤波（1）

一，基本的灰度变换函数
图像增强常用的三类基本函数：线性函数（反转和恒定变换）、对数函数（对数和反对数函数）和幂律函数（n次幂和n次根变换）。恒等函数是最一般的情况，其输出灰度等于输入灰度的变换。

1.1图像反转：
如图所示的反转函数，可得到灰度级范围为[0, L-1]的一幅图像的反转图像，该反转图像由下式给出：
s = L-1-r
这种类型的处理特别适用于增强嵌入在一幅图像的暗区域中的白色或灰色细节。贴别是当黑色编辑在尺寸上占主导地位时。

1.2对数变换
如图对数变换的通用形式为： s=c log(1+r) c:常数并假设r>=0
由上图对数曲线的形状表明，该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值，相反的，对高的输入灰度值也是如此。我们使用这种类型的变换来扩展图像中的暗像素的值，同时压缩更高灰度级的值。反对数变换的作用与此相反。

1.3幂律（伽马）变换
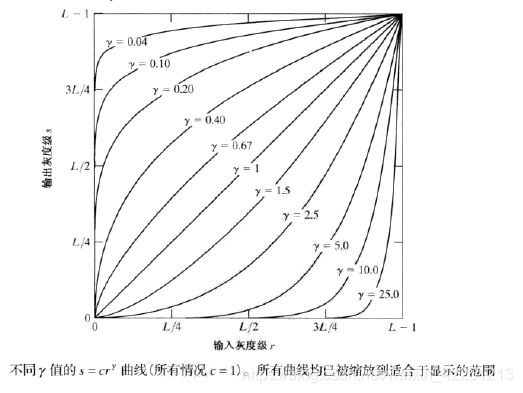
幂律变换的基本形式为： s = cr^γ 其中c和γ 为正常数
该变换将输入中范围较窄的低灰度值映射为输出中较宽范围的灰度值，相反的，对高的输入灰度值也是如此。

1.4分段线性变换函数
对上述三种方法的补充。
1.4.1对比度拉伸
对比度拉伸是扩展图像灰度级动态范围的处理，因此它可以跨越记录介质和装置的全部灰度范围。
1.4.2灰度级分层
一种方法是将感兴趣范围内的所有灰度值显示为一个值，而将其他灰度值显示为另一个值，如二值图像。另一种方法为，是感兴趣范围灰度变亮或变暗，而保持图像中的其他灰度级不变。
1.4.3比特平面分层
像素是由比特组成的数字，例如：256级灰度图像中，每个像素的灰度由8比特组成。

二、直方图处理
2.1直方图均衡变换函数：

n_j=n_k/MN 其中n_k为占比

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

"""
*    Function:            计算新灰度值数组
*    parameter:        
*        pixels           原始像素数组
*    return: 
"""

def getHistogram(pixels):
    GrayValuesCounts = np.zeros(256)
    for rows in pixels:
        for value in rows:
            GrayValuesCounts[value] = GrayValuesCounts[value] + 1
    #data = range(0, 256)
    #if isDisplsy:
    #    plt.bar(data, GrayValuesCounts)
    #    plt.show()

    return GrayValuesCounts

def getGrayValuesChange(pixels):
    sp = pixels.shape
    GrayValuesCounts = getHistogram(pixels)

    temps = np.zeros(256)
    for i in range(0, len(temps)):
        for j in range(0, i + 1):
            temps[i] += 255.0 * GrayValuesCounts[j] / (sp[0] * sp[1])

    return np.round(temps)

"""
*    Function:                  灰度均衡函数
*    parameter:        
*        pixels                 原始像素数组
*        grayValuesNew          灰度值数组
"""
def grayEqualize(str, grayValuesNew):
    out = str
    sp = str.shape

    for i in range(0, sp[0]):
        for j in range(0, sp[1]):
            out[i][j] = grayValuesNew[str[i][j]]

    return out

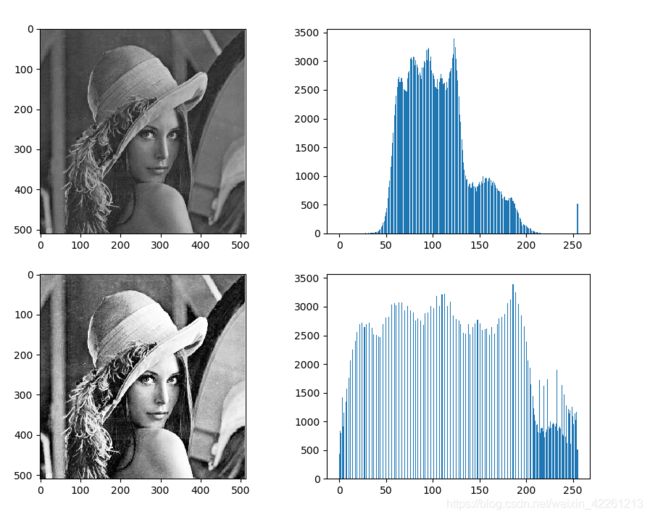
if __name__ == '__main__':
    pic = cv.imread('picture/histogram.png', 0)

    grayValuesNew = getGrayValuesChange(pic)
    data = range(0, 256)

    plt.subplot(2, 2, 1)
    plt.imshow(pic, cmap='gray')

    plt.subplot(2, 2, 2)
    plt.bar(data, getHistogram(pic))

    imag = grayEqualize(pic, grayValuesNew)

    plt.subplot(2, 2, 3)
    plt.imshow(imag, cmap='gray')

    plt.subplot(2, 2, 4)
    plt.bar(data, getHistogram(imag))

    plt.show()

2.2直方图匹配（规定化）

#直方图规定化的实现可以分为一下三步：
#- 计算原图像的累积直方图
#- 计算规定直方图的累积直方图
#- 计算两累积直方图的差值的绝对值
#- 根据累积直方图差值建立灰度级的映射
"""
*    Function:                  直方图规划函数
*    parameter:        
*        strPath                   源图像路径
*        dirPath                   目标图像路径
"""
def histogramMatch(strPath, dirPath):
    strPic = cv.imread(strPath, 0)
    dirPic = cv.imread(dirPath, 0)

    strEqualizeFunc = getEqualizeFunc(strPic)
    dirEqualizeFunc = getEqualizeFunc(dirPic)

    for i in(range(0, len(strEqualizeFunc))):
        index = 0;
        min = np.abs(dirEqualizeFunc[0] - strEqualizeFunc[i])
        for j in (range(0, len(dirEqualizeFunc))):
            if (np.abs(dirEqualizeFunc[j] - strEqualizeFunc[i]) < min):
                min = np.abs(dirEqualizeFunc[j] - strEqualizeFunc[i])
                index = j

        strEqualizeFunc[i] = index
        
    pic = grayEqualize(strPic, strEqualizeFunc)
    
    data = range(0, 256)
    plt.subplot(1, 2, 1)
    plt.imshow(pic, cmap='gray')
    plt.subplot(1, 2, 2)
    plt.bar(data, getHistogram(pic))
    plt.show()

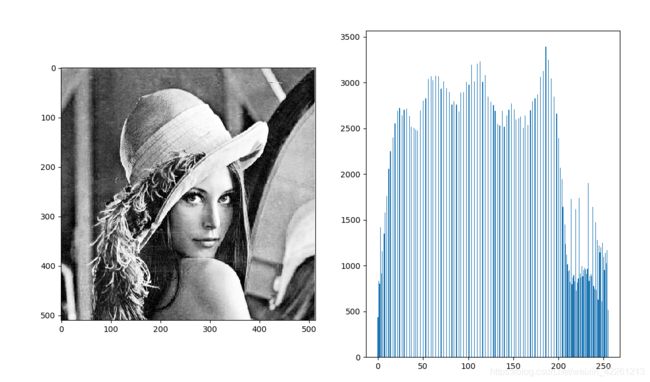
opencv函数：
void calcHist( const Mat* images, int nimages, const int* channels, InputArray mask, OutputArray hist, int dims, const int* histSize, const float** ranges, bool uniform = true, bool accumulate = false );
其参数如下：
images，输入图像的数组，这些图像要有相同大大小，相同的深度（CV_8U CV_16U CV_32F）.
nimages ，输入图像的个数
channels，要计算直方图的通道个数。
mask，可选的掩码，不使用时可设为空。要和输入图像具有相同的大小，在进行直方图计算的时候，只会统计该掩码不为0的对应像素
hist，输出的直方图
dims，直方图的维度
histSize，直方图每个维度的大小
ranges，直方图每个维度要统计的灰度级的范围
uniform，是否进行归一化，默认为true
accumulate，累积标志，默认值为false。

来自 https://www.cnblogs.com/wangguchangqing/p/7098213.html

2.3 局部直方图处理

全局直方图处理可能会导致增强图像中小区域的细节被忽略。解决方法是以图像中每个像素的领域中的灰度分布为基础设计变换函数。

2.4 图像增强中使用直方图统计

直接从直方图获得的统计参数可用于图像增强。令r表示在区间 [r, L-1] 上代表灰度值的一个离散随机变量，并令P(r_i)表示对应于r_i值的归一化直方图分量。可以把P(r_i)看成是得到直方图的那副图像的灰度r_i出现的概率的估计。
r关于其均值的n阶矩定义为：

其中m是r的均值：

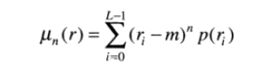
当n=2时，我们将表达式成为灰度方差，通常用σ^2表示。均值是平均灰度的表示，方差是图像对比度的度量。

局部增强公式为：


经验值