概述
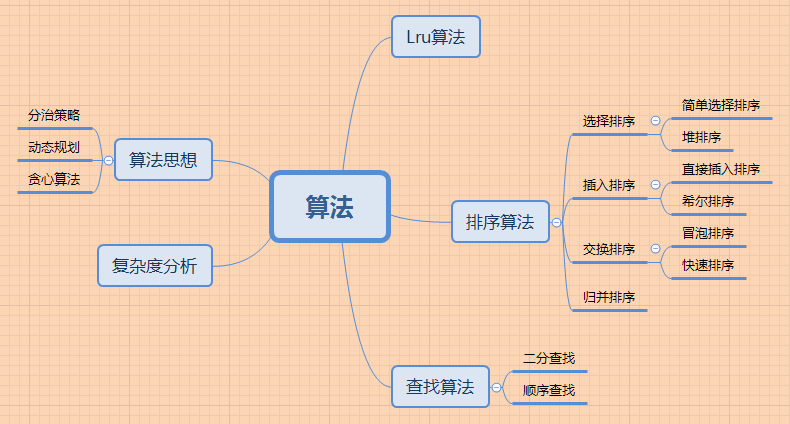
前面花了很多时间研究数据结构,就是为算法的分析作铺垫,从今天开始打算分析一下算法,先看一下算法的整体分类:
Android中其实平时用到的算法比较少,因为JDK跟SDK都帮我封装好了,在看Java源码跟Android源码的时候,里面实际上用到了很多算法,比如集合中查找算法就有二分查找,还有图片加载框架中常用的LruCache,查找算法比较简单,Lru算法是基于LinkedHashMap的,前面已经分析过LinkedHashMap的源码,通过插入和使用的顺序,当内存或者硬盘空间超过之前设定的时候,会自动移除掉最近最少使用的对象,所以重点还是分析一下经典的排序算法。
正文
常见的排序算法可以分为四大类,选择排序,插入排序,交换排序以及归并排序,下面就一一来看一下他们的各自的特点及实现
选择排序
1、简单选择排序:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
步骤
- 1.在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 2.再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 3.以此类推,直到所有元素均排序完毕。
代码实现:
public static > void sort(T[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
// 寻找[i, n)区间里的最小值的索引
int minIndex = i;
for (int j = i + 1; j < n; j++)
// 使用compareTo方法比较两个Comparable对象的大小
if (arr[j].compareTo(arr[minIndex]) < 0)
minIndex = j;
swap(arr, i, minIndex);
}
}
排序测试
public static void main(String[] args) {
// 测试排序算法辅助函数
int N = 10;
//生成10个0到100的随机数
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
//进行排序
SelectionSort.sort(arr);
//打印数组
SortTestHelper.printArray(arr);
}
排序结果:11 16 19 28 43 47 59 72 94 96
2、堆排序:采用二叉堆的数据结构来实现的,虽然实质上还是一维数组。二叉堆是一个近似完全二叉树
步骤
- 1.构造最大堆(Build_Max_Heap):若数组下标范围为0~n,考虑到单独一个元素是大根堆,则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始,向前依次构造大根堆,这样就能保证,构造到某个节点时,它的左右子树都已经是大根堆。
- 2.堆排序(HeapSort):由于堆是用数组模拟的。得到一个大根堆后,数组内部并不是有序的。因此需要将堆化数组有序化。思想是移除根节点,并做最大堆调整的递归运算。第一次将heap[0]与heap[n-1]交换,再对heap[0...n-2]做最大堆调整。第二次将heap[0]与heap[n-2]交换,再对heap[0...n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间,故操作完后整个数组就是有序的了。
- 3.最大堆调整(Max_Heapify):该方法是提供给上述两个过程调用的。目的是将堆的末端子节点作调整,使得子节点永远小于父节点 。
代码实现:
public static void main(String[] args) {
MaxHeap maxHeap = new MaxHeap(100);
int N = 10; // 堆中元素个数
int M = 100; // 堆中元素取值范围[0, M)
for (int i = 0; i < N; i++)
maxHeap.insert((int) (Math.random() * M));
}
排序测试:
Integer[] arr = new Integer[N];
// 将maxheap中的数据逐渐使用extractMax取出来
// 取出来的顺序应该是按照从大到小的顺序取出来的
for (int i = N - 1; i > 0; i--) {
arr[i] = maxHeap.extractMax();
System.out.print(arr[i] + " ");
}
排序结果:99 93 82 82 81 77 64 47 39
插入排序
直接插入排序:对于每个未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
步骤
- 1.从第一个元素开始,该元素可以认为已经被排序
- 2.取出下一个元素,在已经排序的元素序列中从后向前扫描
- 3.如果被扫描的元素(已排序)大于新元素,将该元素后移一位
- 4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 5.将新元素插入到该位置后
- 6.重复步骤2~5
代码实现
public static void sort(Comparable[] arr) {
int n = arr.length;
for (int i = 0; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
// 写法1
for (int j = i; j > 0; j--)
if (arr[j].compareTo(arr[j - 1]) < 0)
swap(arr, j, j - 1);
else
break;
}
}
排序测试:
public static void main(String[] args) {
int N = 10;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
sort(arr);
SortTestHelper.printArray(arr);
}
排序结果:3 8 13 15 34 40 65 72 77 95
希尔排序:也称递减增量排序算法,实质是分组插入排序。由 Donald Shell 于1959年提出。希尔排序是非稳定排序算法
步骤
- 1.获得一个无序的序列 T0 = [4, 3, 6, 5, 9, 0, 8, 1, 7, 2],并计算出当前序列状态下的步长 step = length / 3 + 1
- 2.对序列 T0 按照步长周期分组
- 3.对每个子序列进行插入排序操作
- 4.判断此时的步长 step 是否大于 1?如果比 1 小或是等于 1,停止分组和对子序列的插入排序,否则,就继续;
- 5.修改此时的步长 step = step / 3 + 1,并继续第 2 到第 4 步;
- 6.排序算法结束,序列已是一个整体有序的序列。
代码实现
public static void sort(Comparable[] arr){
int n = arr.length;
for( int i = 0 ; i < n ; i ++ ){
// 寻找[i, n)区间里的最小值的索引
int minIndex = i;
for( int j = i + 1 ; j < n ; j ++ )
// 使用compareTo方法比较两个Comparable对象的大小
if( arr[j].compareTo( arr[minIndex] ) < 0 )
minIndex = j;
swap( arr , i , minIndex);
}
}
排序测试
public static void main(String[] args) {
int N = 10;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
sort(arr);
SortTestHelper.printArray(arr);
}
排序结果:1 10 13 33 39 40 47 56 90 93
交换排序
冒泡排序:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
步骤
- 1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 2.对第0个到第n-1个数据做同样的工作。这时,最大的数就“浮”到了数组最后的位置上。
- 3.针对所有的元素重复以上的步骤,除了最后一个。
- 4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
代码实现
public static void sort(Comparable[] arr){
int n = arr.length;
for( int i = 1 ; i < n ; i ++ )
for (int j = i; j < arr.Length; j++){
if( arr[i-1].compareTo(arr[i]) > 0 ){
swap( arr , i-1 , i );
}
}
}
排序测试
public static void main(String[] args) {
int N = 10;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
sort(arr);
SortTestHelper.printArray(arr);
}
排序结果:6 6 29 31 34 35 52 67 75 100
快速排序:通常明显比同为Ο(n log n)的其他算法更快,因此常被采用,而且快排采用了分治法的思想,所以在很多笔试面试中能经常看到快排的影子。可见掌握快排的重要性。
步骤
- 1.从数列中挑出一个元素作为基准数。
- 2.分区过程,将比基准数大的放到右边,小于或等于它的数都放到左边。
- 3.再对左右区间递归执行第二步,直至各区间只有一个数。
代码实现
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r) {
if (l >= r)
return;
int p = partition(arr, l, r);
sort(arr, l, p - 1);
sort(arr, p + 1, r);
}
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(Comparable[] arr, int l, int r) {
Comparable v = arr[l];
int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
for (int i = l + 1; i <= r; i++)
if (arr[i].compareTo(v) < 0) {
j++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
排序测试
// 测试 QuickSort
public static void main(String[] args) {
// Quick Sort也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 10;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
sort(arr, 0, arr.length - 1);//
// SortTestHelper.testSort("bobo.algo.QuickSort", arr);
}
排序结果:13 17 18 28 38 39 45 61 71 78
归并排序
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。先考虑合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
步骤
- 1.将数组从中间分开,对两边分别排序。
- 2.将两个有序的数组进行合并。
代码实现:
// 递归使用归并排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r) {
// 对于小规模数组, 使用插入排序
if (r - l <= 15) {
InsertionSort.sort(arr, l, r);
return;
}
int mid = (l + r) / 2;
sort(arr, l, mid);
sort(arr, mid + 1, r);
// 对于arr[mid] <= arr[mid+1]的情况,不进行merge
// 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
if (arr[mid].compareTo(arr[mid + 1]) > 0)
merge(arr, l, mid, r);
}
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
private static void merge(Comparable[] arr, int l, int mid, int r) {
Comparable[] aux = Arrays.copyOfRange(arr, l, r + 1);
// 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1
int i = l, j = mid + 1;
for (int k = l; k <= r; k++) {
if (i > mid) { // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j - l];
j++;
} else if (j > r) { // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i - l];
i++;
} else if (aux[i - l].compareTo(aux[j - l]) < 0) { // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i - l];
i++;
} else { // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j - l];
j++;
}
}
}
排序测试:
public static void main(String[] args) {
int N = 10;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100);
sort(arr, 0, arr.length - 1);
SortTestHelper.printArray(arr);
}
排序结果:6 9 16 24 38 55 57 66 67 86