计算领域中的数学知识都有哪些?
二进制是计算机系统的基础,余数被运用在很多常见的算法和数据结构中,而布尔代数是编程中控制逻辑的灵魂。
二进制、余数和布尔代数
1 二进制
许多专业人士都认为计算机的起源来自数学中的二进制计数法。这样的观点颇有道理。可以说,没有二进制,就没有如今的计算机系统。那么什么是二进制呢?为什么计算机要使用二进制而不是我们日常生活中的十进制呢?如何在代码中操作二进制呢?在这里我们将从计算机的起源——二进制出发,讲解它在计算机中的“玄机”。
2 余数
余数就是指整数除法中被除数未被除尽的部分,且余数的取值范围为0到除数之间(不包括除数自身)。例如,27除以11,商为2,余数为5。可能你会纳闷,小学生就能懂的内容,还需要在这里专门拿出来说吗?可不要小看余数,无论是在日常生活中,还是计算机领域中,它都发挥着重要的作用。
3 布尔代数
在实际生活中,需要遵守各种各样的规则。那么,如何将这些规则表述清楚并且没有异议呢?逻辑和集合就是我们最好的帮手。它们可以消除自然语言所产生的歧义,并严格准确地描述事物。对于以“严谨”而著称的计算机,逻辑命题及其相关的运算就更显得意义重大了。作为程序员,如果不能很好地理解这些概念,就会对计算机无从下手。所以,很有必要来讲一下逻辑和集合,以及它们的基础——布尔代数。
排列、组合和动态规划
1 排列
“田忌赛马”的故事大家都听过,田忌是齐国有名的将领,他常常和齐王赛马,可是总是败下阵来,心中非常不悦。孙膑想帮田忌。他将这些马分为上、中、下三等。他让田忌用自己的下等马来应战齐王的上等马,用上等马应战齐王的中等马,用中等马应战齐王的下等马。3场比赛结束后,田忌只输了第一场,赢了后面两场,最终赢得与齐王的整场比赛。孙膑每次都从田忌的马匹中挑选出一匹,一共进行3次,排列出战的顺序,这其实就是数学中的排列过程。从
![]()
个不同的元素中取出
![]()
(1
![]()
![]()
![]()
![]()
)个不同的元素,按照一定的顺序排成一列,这个过程就叫排列(permutation)。当出现
![]()
这种特殊情况的时候,例如,在田忌赛马的故事中,田忌的3匹马必须全部出战,这就是全排列(all permutation)。如果选择出的这
![]()
个元素可以有重复的,这样的排列就是可重复排列(permutation with repetition),否则就是不可重复排列(permutation without repetition)。
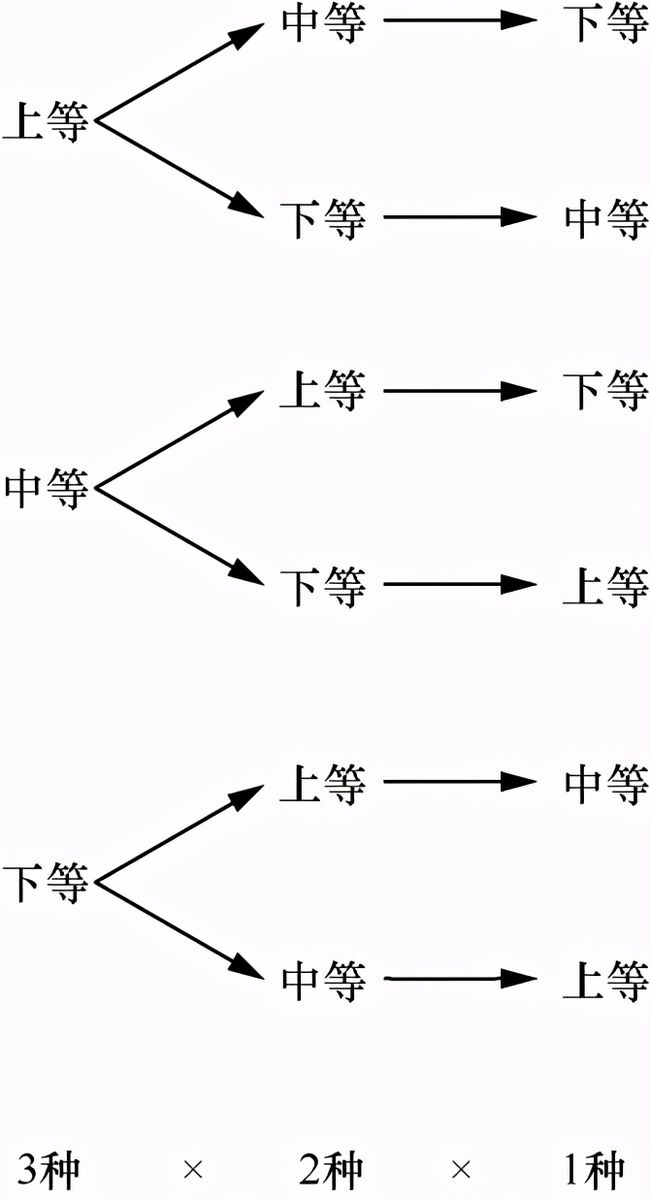
图3-1展示了田忌赛马案例中的排列情况。
图3-1 田忌赛马中的排列情况
从图3-1可以看出,所有可能性通过一个树状结构表达。从树的根结点到叶结点,每种路径都是一种排列。有多少个叶结点就有多少种全排列,最终叶结点的数量是
![]()
,所以最终排列的数量为6。我们用
![]()
、
![]()
和
![]()
分别表示田忌的上、中、下等马跑完全程所需的时间,用
![]()
、
![]()
和
![]()
分别表示齐王的上、中、下等马跑完全程所需的时间,设定为
![]()
。如果你将这些可能的排列,仔细地和齐王的上、中、下等马进行对比,只有{下等, 上等, 中等}这一种可能战胜齐王,也就是
![]()
,
![]()
,
![]()
。
对于通用案例中最终排列的数量,我们可以得到如下结论。
- 对于个元素的全排列,所有可能的排列数量就是,也就是;
- 对于从个元素里取出(0<)个元素的不重复排列数量是 ,也就是。
这两点都是可以用数学归纳法证明的,有兴趣的话你可以自己尝试一下。
我们刚才讨论了3匹马的情况,如果有30匹马、300匹马,会发生什么呢?30的阶乘已经是天文数字了。更糟糕的是,如果两组马之间的速度关系也是非常随机的,例如
![]()
,那就不能再使用“己方最差的马和对方最好的马比赛”这种战术了。手工计算肯定是算不过来了,这个时候计算机可以帮大忙。我们将使用代码来展示如何生成所有的排列。如果你细心的话,就会发现在新版舍罕王赏麦的案例中,其实已经涉及了排列的思想,不过那个案例不是以“选取多少个元素”为终止条件,而是以“选取元素的总和”为终止条件。尽管这样,我们仍然可以使用递归的方式来快速地实现排列。
首先,在不同的选马阶段,我们都要保存已经有几匹马出战、它们的排列顺序以及还剩几匹马没有选择。我使用变量result来存储到当前函数操作之前已经出战的马匹及其排列顺序,而变量horses存储到当前函数操作之前还剩几匹马尚未出战。变量new_result和rest_horses分别从result和horses克隆而来,保证不会影响上一次的结果。其次,孙膑的方法之所以奏效,是因为他看到每一等马中,田忌的马只比齐王的差一点点。如果相差太多,可能就会有不同的胜负结果。所以,在设定马匹跑完全程的时间上,我特意设定为
![]()
,只有这样才能保证计算机得出和孙膑相同的结论。基于这两点,代码清单3-1展示了实现细节。
代码清单3-1 田忌赛马中排列的实现
# 齐王赛马及其跑完全程所需的时间
q_horses = ['q1', 'q2', 'q3']
q_horses_time = {'q1': 1.0, 'q2': 2.0, 'q3': 3.0}
# 田忌赛马及其跑完全程所需的时间
t_horses = ['t1', 't2', 't3']
t_horses_time = {'t1': 1.5, 't2': 2.5, 't3': 3.5}
# 找出所有的排列
def permutate(horses, selection):
# 没有多余的马匹供选择
if len(horses) == 0:
print(selection)
# 比较田忌和齐王的马匹,看哪方获胜
compare(selection, q_horses)
for each in horses:
# 从剩余的未出战马匹中,选择一匹,加入结果
new_selection = selection.copy()
new_selection.append(each)
# 将已选择的马匹从未出战的列表中移出
rest_horses = horses.copy()
rest_horses.remove(each)
# 递归调用,对于剩余的马匹继续生成排列
permutate(rest_horses, new_selection)
# 比较田忌和齐王的马匹,看哪方获胜
def compare(t, q):
t_won_cnt = 0
for i in range(0, len(t)):
print(t_horses_time[t[i]], ' ', q_horses_time[q[i]])
if t_horses_time[t[i]] < q_horses_time[q[i]]:
t_won_cnt += 1
if t_won_cnt > (len(t) / 2):
print('田忌获胜!')
else:
print('齐王获胜!')
if __name__ == '__main__':
# 下面是测试代码。当然你可以设置更多的马匹,并增加相应的马匹跑完全程的时间
permutate(t_horses, [])从最终的运行结果可以看出,6种排列中只有一种情况是田忌获胜的。如果田忌不听从孙膑的建议,而是随机安排马匹出战,那么他只有1/6的获胜概率。如果齐王也是随机安排他的马匹出战顺序,又会是怎样的结果呢?如果手工来实现的话,大体思路是为田忌和齐王双方都生成他们各自马匹的全排列,然后再做交叉对比,看哪方获胜。这个交叉对比的过程也是一个排列的问题,田忌这边有6种顺序,而齐王这边也有6种顺序,所以一共的可能性是
![]()
种。代码清单3-2对整个过程进行了模拟。
代码清单3-2 田忌和齐王都随机安排赛马的模拟
# 找出并保存所有的排列组合,selection保存一个排列,result_set保存所有可能的排列
def permutate_and_save(horses, selection, result_set):
# 没有多余的马匹供选择,记录排列
if len(horses) == 0:
result_set.append(selection)
for each in horses:
# 从剩余的未出战马匹中,选择一匹,加入结果
new_selection = selection.copy()
new_selection.append(each)
# 将已选择的马匹从未出战的列表中移出
rest_horses = horses.copy()
rest_horses.remove(each)
# 递归调用,对于剩余的马匹继续生成排列
permutate_and_save(rest_horses, new_selection, result_set)
if __name__ == '__main__':
t_result_set = []
permutate_and_save(t_horses, [], t_result_set)
q_result_set = []
permutate_and_save(q_horses, [], q_result_set)
print(t_result_set)
print(q_result_set)
# 两两比较看输赢
for each_t in t_result_set:
for each_q in q_result_set:
compare(each_t, each_q)因为交叉对比时只需要选择2个元素,分别是田忌的出战顺序和齐王的出战顺序,所以这里使用2层循环的嵌套来实现。从最后的结果可以看出,田忌获胜的概率仍然是1/6。在概率中,排列有很大的作用,因为排列会帮助我们列举出随机变量取值的所有可能性,用于生成这个变量的概率分布,之后在第二篇“概率统计”中还会具体介绍。此外,排列在计算机领域中有着很多应用场景。这里讲讲最常见的密码的暴力破解。先来看2017年网络安全界的两件大事。第一件发生在2017年5月,新型蠕虫式勒索病毒WannaCry爆发。当时这个病毒蔓延得非常迅速,计算机被感染后,其中的文件会被加密锁住,黑客以此会向用户勒索比特币。第二件和美国的信用评级公司Equifax有关。仅在2017年内,这个公司就被黑客盗取了大约1.46亿用户的数据。黑客攻击的方式多种多样,手段变得越来越高明,但是窃取系统密码仍然是最常用的攻击方式。有时候,黑客们并不需要真的拿到你的密码,而是通过“猜”,也就是列举各种可能的密码,然后逐个地去尝试密码的正确性。如果某个尝试的密码正好和原先管理员设置的一样,那么系统就被破解了。这就是常说的暴力破解法。
假设一个密码是由英文字母组成的,那么每位密码有52种选择,也就是大小写字母加在一起的数量。那么,生成
![]()
位密码的可能数量就是
![]()
种。也就是说,从
![]()
(这里
![]()
为52)个元素取出
![]()
(0<
![]()
![]()
![]()
)个元素的可重复全排列,总数量为
![]()
。如果你遍历并尝试所有的可能性,就能破解密码了。不过,即使存在这种暴力破解法,你也不用担心自己的密码很容易被人破解,因为我们平时需要使用密码登录的网站或者移动端App基本上都限定了一定时间内尝试密码的次数,例如1天之内只能尝试5次等。这些次数一定远远小于密码排列的可能数量。这也是有些网站或App要求你一定使用多种类型的字符来创建密码的原因,如字母加数字加特殊符号。因为类型越多,
![]()
中的
![]()
越大,可能数量就越多。如果使用英文字母的4位密码,就有
![]()
种,超过了730万种。如果在密码中再加入0~9这10个阿拉伯数字,那么可能数量就是
![]()
种,超过了1400万种。同理,也可以增加密码长度,也就是用
![]()
中的
![]()
来实现这一点。如果在英文字母和阿拉伯数字的基础上,将密码的长度增加到6位,就是
![]()
种,已经超过568亿种了!这还没有考虑键盘上的各种特殊符号。有人估
算了一下,如果用上全部256个ASCII码字符,设置长度为8的密码,那么一般的黑客需要10年左右的时间才能暴力破解这种密码。
2 组合
2018世界杯足球赛的激烈赛况大家现在还记忆犹新吧?你知道这场足球盛宴的比赛日程是怎么安排的吗?如果现在你是组委会成员,会怎么安排比赛日程呢?可以用上一节的排列思想,让全部的32支入围球队都和其他球队进行一次主客场的比赛。自己不可能和自己比赛,因此在这种不可重复的排列中,主场球队有32种选择,而客场球队有31种选择。那么一共要进行多少场比赛呢?很简单,就是
![]()
场!这个数字非常夸张,即使一天看2场,也要1年多才能看完。即使球迷开心了,可是每队球员要踢主客场共62场,早已累趴下了。既然这样,是否可以取消主客场制,让任意两个球队之间只踢1场呢?取消主客场,这就意味着两个球队之间的比赛由2场降为1场,那么所有比赛场数就是
![]()
场,还是很多。这就是要将所有32支球队分成8个小组先进行小组赛的原因。一旦分成小组,每个小组的比赛场数就是
![]()
场。所有小组赛就是
![]()
场。再加上在16强阶段开始采取淘汰制,两两淘汰,所以需要
![]()
场淘汰赛(最后一次加2是因为还有3、4名的比赛),那么整个世界杯决赛阶段就有
![]()
场比赛。当然,说了这么多,你可能会好奇,这两两配对比赛的场次,我是如何计算出来的?让我引出本节要讲的概念——组合(combination)。
组合可以说是排列的兄弟,两者类似但又有所不同,这两者的区别在于:组合是不考虑每个元素出现的顺序的。从定义上来说,组合是指,从
![]()
个不同元素中取出
![]()
(1
![]()
![]()
![]()
![]()
)个不同的元素。例如,前面说到的世界杯足球赛的例子,从32支球队里找出任意2支球队进行比赛,就是从32个元素中取出2个元素的组合。如果将上一讲中田忌赛马的规则改一下,改为从10匹马里挑出3匹比赛,但是并不关心这3匹马的出战顺序,那么这也是一个组合的问题。对于所有
![]()
取值的组合之全集合,可以叫作全组合(all combination)。例如,对集合{1, 2, 3}而言,全组合就是{空集, {1}, {2}, {3}, {1, 2}, {1, 3} {2, 3}, {1, 2, 3}}。
如果安排足球比赛时不考虑主客场,也就是不考虑两支球队的顺序,两支球队之间只要踢一场就行了。那么从
![]()
个元素取出
![]()
个的组合,有多少种可能数量呢?假设某项运动需要3支球队一起比赛,那么32支球队就有
![]()
种排列,如果3支球队在一起只要比一场,那么我们要抹除多余的比赛。3支球队按照任意顺序的比赛有
![]()
场,所以从32支球队里取出3支球队的组合是
![]()
。基于此,我们可以扩展成以下两种情况。
(1)
![]()
个元素里取出
![]()
个的组合,其可能数量就是从
![]()
个里取
![]()
个的排列数量除以
![]()
个全排列的数量,也就是
![]()
。
(2)对全组合而言,可能数量为
![]()
种。例如,当
![]()
的时候,全组合包括了8种情况。
这两点都可以用数学归纳法证明,有兴趣的话你可以自己尝试一下。
在3.1节中我们用递归实现了全排列。全组合就是将所有元素列出来,没有太大意义,所以这里阐述如何使用递归从3个元素中选取2个元素的组合。我们假设有3支球队,即
![]()
、
![]()
和
![]()
。从图3-2可以看出,对组合而言,{
![]()
,
![]()
}已经出现了,因此无需{
![]()
,
![]()
}。同理,{
![]()
,
![]()
}已经出现了,因此无需{
![]()
,
![]()
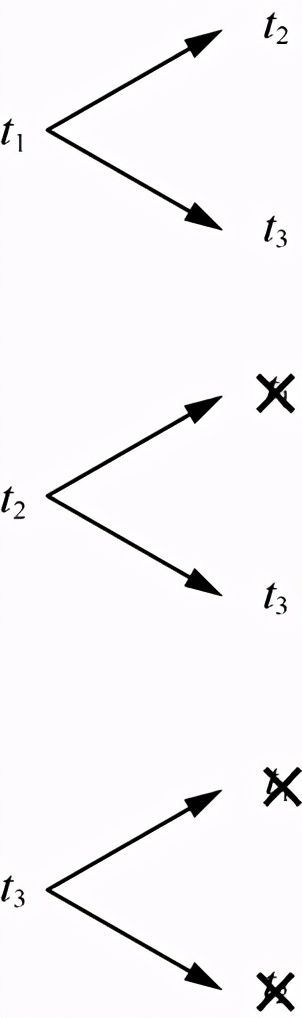
}等。对于重复的组合,图3-2用叉划掉了。这样,最终只有3种组合了。
图3-2 田忌赛马中的组合情况
那么,如何使用代码来实现呢?下面是一种最简单粗暴的做法。
(1)先实现排列的代码,输出所有的排列。例如,{
![]()
,
![]()
}, {
![]()
,
![]()
}。
(2)针对每种排列,对其中的元素按照一定的规则排序。上述两种排列经过排序后就是{
![]()
,
![]()
}, {
![]()
,
![]()
}。
(3)对排序后的排列,去掉重复的那些排列。上述两种排列最终只保留一个{
![]()
,
![]()
}。
这样做效率就会比较低,很多排列生成之后,最终还是要被当作重复的结果去掉。显然,还有更好的做法。从图3-2可以看出,被划掉的那些元素都是那些出现顺序和原有顺序颠倒的元素。例如,在原有集合中,
![]()
在
![]()
的前面,所以我们划掉了{
![]()
,
![]()
}的组合。这是因为,我们知道
![]()
出现在
![]()
之前,
![]()
的组合中一定已经包含了
![]()
,所以
![]()
的组合就无须再考虑
![]()
了。因此,我只需要在原有的排列代码上稍作修改,每次传入嵌套函数的剩余元素,即不再是所有的未选择元素,而是出现在当前被选元素之后的那些元素。具体如代码清单3-3所示。
代码清单3-3 球队组合的实现
# 使用函数的递归(嵌套)调用,找出所有可能的组合
# teams保存了目前还未参与组合的球队,selection保存了当前已经组合的球队,m表示要选择的球队数量
def combine(teams, selection, m):
# 挑选完了m个球队,输出结果
if len(selection) == m:
print(selection)
return
for i in range(0, len(teams)):
new_selection = selection.copy()
new_selection.append(teams[i])
rest_teams = teams[i + 1:len(teams)]
combine(rest_teams, new_selection, m)
if __name__ == '__main__':
# 这段测试代码,从3个元素中选择2个元素的所有组合
teams = ['t1', 't2', 't3']
combine(teams, [], 2)组合在计算机领域中也有很多的应用场景,例如大型比赛中赛程的自动安排、多维度的数据分析以及自然语言处理的优化等。这里用组合的思想来提升自然语言处理的性能。在搜索引擎中,通常会将每篇很长的文章分割成一个个的单词,然后对每个单词进行索引,便于日后的查询。但是很多时候,光有单个的单词是不够的,还要考虑多个单词所组成的词组。例如,“red bluetooth mouse”这样的词组。处理词组最常见的一种方式是多元文法,也就是将临近的几个单词合并起来,形成一个新的词组。例如,可以将“red”和“bluetooth”合并为“red bluetooth”,还可以将“bluetooth”和“mouse”合并为“bluetooth mouse”。设计多元文法只是为了方便计算机的处理,而不考虑组合后的词组是不是有正确的语法和语义。例如“red bluetooth”,从语义的角度来看,这个词组就很奇怪。但是毕竟还会生成很多合理的词组,例如“bluetooth mouse”。所以,如果不进行深入的语法分析,其实没办法区分哪些多元词组是有意义的,哪些是没有意义的,因此最简单的做法就是保留所有词组。
普通的多元文法本身存在一个问题,那就是定死了每个元组内单词出现的顺序。例如,原文中可能出现的是“red bluetooth mouse”,可是用户在查询的时候可能输入的是“bluetooth mouse red”。这么输入肯定不符合语法,但实际上互联网上的用户经常会这么做。在这种情况下,如果只保留原文的“red bluetooth mouse”,就无法将其和用户输入的“bluetooth red mouse”匹配了。如果不要求查询词组中单词出现的顺序和原文一致,那么该怎么办呢?一种做法是,将每个二元组或三元组进行全排列,得到所有的可能,但是这样的话,二元组的数量就会增加1倍,三元组的数量就会增加5倍,一篇文章的数据保存量就会增加3倍左右。另一种做法是,对用户查询做全排列,将原有的二元组查询变为2个不同的二元组查询,将原有的三元组查询变为6个不同的三元组查询,但是事实是,这样会增加实时查询的耗时。这时可以运用组合。多个单词出现时,我们并不关心它们的顺序(也就是不关心排列),而只关心它们的组合。无须关心顺序就意味着可以对多元组内的单词进行某种形式的标准化。即使原来的单词出现顺序有所不同,经过这个标准化过程之后,也会变成唯一的顺序。例如,“red bluetooth mouse”,这3个词排序后就是“bluetooth, mouse, red”,而“bluetooth red mouse”排序后也是“bluetooth, mouse, red”,自然两者就能匹配上了。我们所需要做的事情,就是在保存文章多元组和处理用户查询这两个阶段分别进行这种排序。这样既可以减少保存的数据量,同时又可以减少查询的耗时。这个问题很容易就解决了。
此外,组合思想还广泛应用在多维度的数据分析中。例如,我们要设计一个连锁店的销售业绩报表,这张报表含有若干属性,包括分店名称、所在城市、销售品类等。其中,最基本的汇总数据包括每个分店的销售额、每个城市的销售额、每个品类的销售额。除了这些最基本的数据,还可以利用组合的思想生成更多的筛选条件。
组合和排列有相似之处,都是从
![]()
个元素中取出若干元素。不过,排列考虑了取出的元素之间的顺序,而组合无须考虑这种顺序,这是排列和组合最大的区别。因此,组合适合找到多个元素之间的联系而并不在意它们之间的先后顺序,例如多元文法中的多元组,这有利于避免不必要的数据保存或操作。具体到编程,组合和排列两者的实现非常类似。区别在于,组合并不考虑挑选出来的元素是如何排序的。所以,在递归的时候,传入下一个嵌套调用函数的剩余元素中只需要包含当前被选元素之后的那些元素,以避免重复的组合。
3 动态规划
排列和组合会列举全部可能的情况,经常被用在穷举算法之中。不过,有的时候并不需要暴力地查找所有可能,而只要找到最优解,那么就可以考虑另一种数学思想——动态规划(dynamic programming)。本节我将通过文本搜索的话题来讲一下查询推荐(query suggestion)的实现过程,以及它所使用的动态规划思想。
树和图
1 图和树的概念
简单地说,图由边和结点组成。如果一个图里所有的边都是有向边,那么这个图就是有向图。如果一个图里所有的边都是无向边,那么这个图就是无向图。既包含有向边又包含无向边的图称为混合图。在有向图中,以结点
![]()
为出发点的边的数量,叫作
![]()
的出度;以
![]()
为终点的边的数量,叫作
![]()
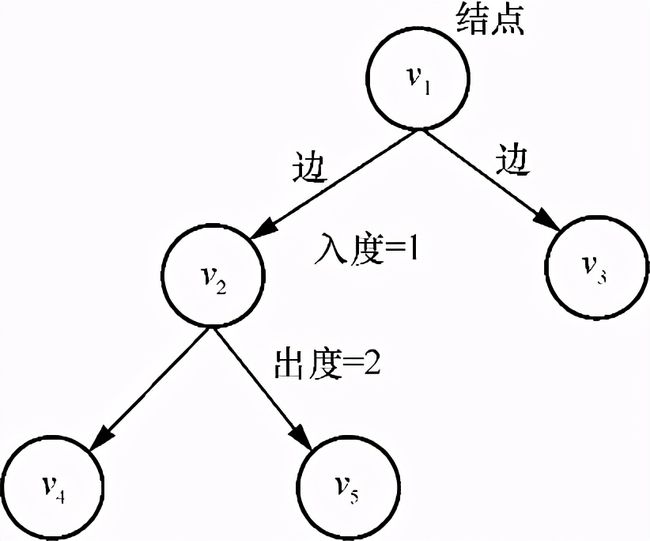
的入度。在图4-1展示的有向图中,结点
![]()
的入度是1,出度是2。
图4-1 结点、边、出度和入度
另外几个和图有关的概念是通路、回路和连通。结点和边交替组成的序列就是通路。所以,通路上的任意两个结点是互为连通的。如果一条通路的起始结点
![]()
和终止结点
![]()
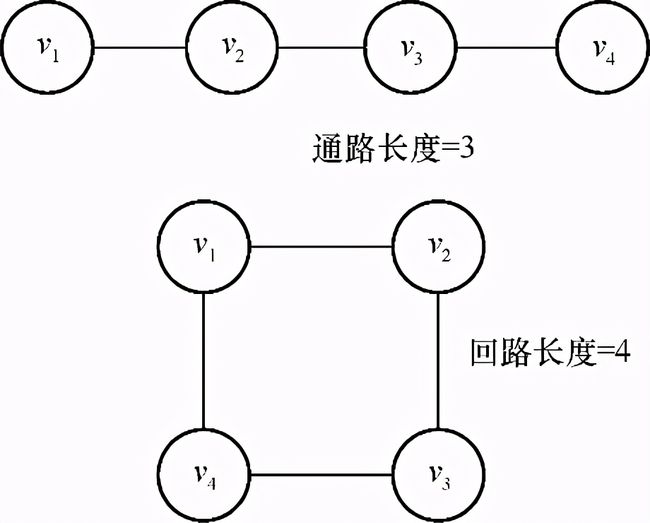
相同,这种特殊的通路就叫作回路。从起始结点到终止结点所经过的边之数量,就是通路的长度。图4-2展示了一条通路和一条回路,第一条非回路通路的长度是3,第二条回路的长度是4。
图4-2 长度为3的通路和长度为4的回路
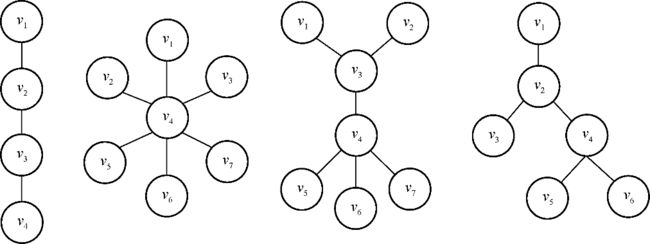
理解了图的基本概念,再来看树和有向树。树是一种特殊的图,它是没有简单回路的连通无向图。这里的简单回路其实就是指,除了第一个结点和最后一个结点相同外,其余结点不重复出现的回路。可以参考图4-3展示的几种树的结构。
图4-3 几种树的结构
接下来我们将重点介绍计算机领域中最常用的树结构——有向树。有向树是一种树,特殊的是,它的边是有方向的,并且满足以下几个条件。
(1)有且仅有一个结点的入度为0,这个结点称为根。
(2)除根以外的所有结点的入度都为1。从树根到任一结点有且仅有一条有向通路。
(3)除了这些基本定义,有向树还有几个重要的概念,包括父结点、子结点、兄弟结点、前辈结点、后辈结点、叶结点、结点的高度(或深度)、树的高度(或深度)。图4-4展示了这些概念,其中根结点的高度被设置为0,根据需要也可以将其设置为1。
图4-4 有向树的基本概念
讲述了有向树的概念,你会发现它的应用是非常广泛的,包括前面在介绍递归和排列组合的章节中你都会发现树的身影。
本文截选自《程序员的数学基础课 从理论到Python实践》
本书紧贴计算机领域,从程序员的需求出发,精心挑选了程序员真正用得上的数学知识,通过生动的案例来解读知识中的难点,使程序员更容易对实际问题进行数学建模,进而构建出更优化的算法和代码。
本书共分为三大模块:“基础思想”篇梳理编程中常用的数学概念和思想,既由浅入深地精讲数据结构与数学中基础、核心的数学知识,又阐明数学对编程和算法的真正意义;“概率统计”篇以概率统计中核心的贝叶斯公式为基点,向上讲解随机变量、概率分布等基础概念,向下讲解朴素贝叶斯,并分析其在生活和编程中的实际应用,使读者真正理解概率统计的本质,跨越概念和应用之间的鸿沟;“线性代数”篇从线性代数中的核心概念向量、矩阵、线性方程入手,逐步深入分析这些概念是如何与计算机融会贯通以解决实际问题的。除了理论知识的阐述,本书还通过Python语言,分享了通过大量实践积累下来的宝贵经验和编码,使读者学有所用。
本书的内容从概念到应用,再到本质,层层深入,不但注重培养读者养成良好的数学思维,而且努力使读者的编程技术实现进阶,非常适合希望从本质上提升编程质量的中级程序员阅读和学习。