前言
高级数据结构难点很多,而且小编接近一年没有碰过代码了,一天能发布的文章数目有限,所以今天决定爆肝一个晚上来一个超长的博客。
但小编能力有限,只会讲解下列几个部分:
- 树、图遍历的基础——搜索
- 队列
- 树的基本知识
- 二叉树
- 二叉排序树
- 平衡树Treap
- 红黑树(待更中……)
- 树状数组
- 线段树
- 图论(待更中……)
实际上这都是我从网上找来的一大堆看似很高级,实则很高级的东西,但是小编会非常详细的记录经验和讲解知识,以及一些实际的例题。
不过图论内容较多,图论将会另更一篇(不过如果想立刻学的话可以看一下我昔日的博客:传送门),届时在章末补上链接。
一、树、图遍历的基础——搜索
在此部分,我们先讲解深度优先搜索(dfs),广度优先搜索就放到队列里面讲。
搜索是至关重要的,因为树,图在遍历时,使用的就是搜索算法,遍历是它们的基本操作之一。
1)前置基础
务必学会递归
2)核心思想
如果你现在正身处一个迷宫中,你想走出迷宫,那么方法主要有两种
-
1>一条路走到黑,不撞南墙不回头,只要认定一个方向,就一直走到边界才掉头
-
2>环顾四周,不停向外扩展,先看离自己近的是不是出口,再看远的
第一种办法靠碰运气,说不准第一次方向就蒙对了,但也有可能运气差到遍历整个地图才能找到。
第二种情况也靠碰运气,说不准终点就在起点旁边,但是也可能运气差到终点在边界处。
我们现在将要讲解的就是第一种办法。
3)谈谈怎么代码实现吧
整个过程是这样的:
void dfs(一些需要传递的信息,来唯一识别当前的状态,例如当前走的次数,当前的位置等)
{
if(判断当前状态是否是目标状态) 如果是就存下这个答案,返回
for(逐个枚举可能的状态)
{
扩展新状态;
if(新状态可以使用)
{
有时需要做标记;
dfs(新状态);
回溯,即撤回标记,防止下次不能再到达这个状态(有时不需要回溯)
}
}
}
具体一点,对于迷宫,要求输出最小步数,可以修改成这样:
void dfs(横坐标,纵坐标,当前步数)
{
if(横坐标==终点横坐标&&纵坐标==终点纵坐标)
{
ans=min(ans,当前步数);
return;
}
for(枚举四个方向,即上下左右)
{
扩展出下一步的横坐标,纵坐标;
if(横坐标、纵坐标没有超出地图范围且这个新地方没有走过)
{
标记这个点走过了;
dfs(新横坐标,新纵坐标,步数+1);
标记这个点没有走过;
}
}
}
例题
例1
对于上面的迷宫,正好小编最近刷了一道规规矩矩的迷宫题。
题目链接:https://www.luogu.com.cn/problem/P1605
对于不想抬起宝贵的手点击链接(因为这样手移动会做功消耗动能,与空气摩擦还要生热)的同志,直接看题吧:
P1605 迷宫
题目背景
给定一个N*M方格的迷宫,迷宫里有T处障碍,障碍处不可通过。给定起点坐标和终点坐标,问: 每个方格最多经过1次,有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
题目描述
无
输入格式
第一行N、M和T,N为行,M为列,T为障碍总数。第二行起点坐标SX,SY,终点坐标FX,FY。接下来T行,每行为障碍点的坐标。
输出格式
给定起点坐标和终点坐标,问每个方格最多经过1次,从起点坐标到终点坐标的方案总数。
输入输出样例
输入 #1
2 2 1
1 1 2 2
1 2
输出 #1
1
说明/提示
【数据规模】
1≤N,M≤5
AC代码
#include
using namespace std;
int n,m,t,ans,sx,sy,fx,fy,a,b;
int edge[100][100],mapp[100][100];
int next[4][2]={{1,0},{-1,0},{0,1},{0,-1}};//下一步怎么走
void dfs(int x,int y)
{
if(x==fx&&y==fy) //判断目标状态
{
ans++;//解的个数增加
return;
}
for(int i=0;i<4;i++)
{
int tx=x+next[i][0];
int ty=y+next[i][1];//扩展出下一步的位置
if(tx<1||ty<1||tx>n||ty>m||mapp[tx][ty]==1||edge[tx][ty]==1) continue; //判断下一步走这个点是否成立
mapp[tx][ty]=1;//标记走过了,防止同一路径重复走造成死循环
dfs(tx,ty);
mapp[tx][ty]=0;//标记回没走过,因为可能另一条路径需要经过这个点
}
}
int main()
{
cin>>n>>m>>t;
cin>>sx>>sy>>fx>>fy;
for(int i=1;i<=t;i++)
{
cin>>a>>b;
edge[a][b]=1;//标记障碍物
}
mapp[sx][sy]=1;
dfs(sx,sy);
cout< 例2
题目链接:https://www.luogu.com.cn/problem/P1135
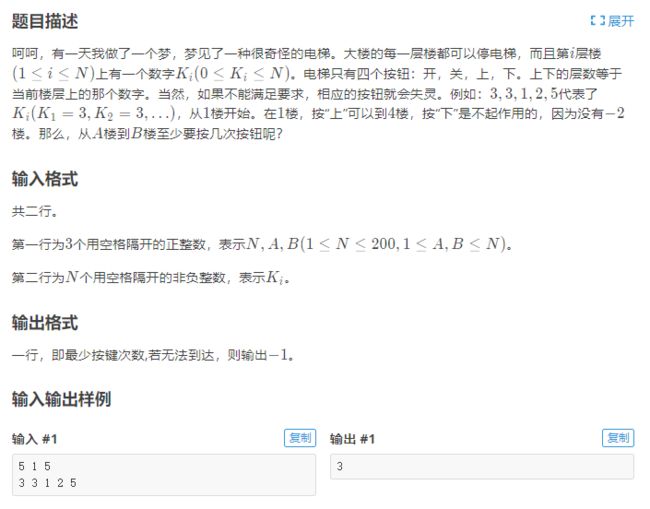
P1135 奇怪的电梯
解析
当然,深度优先搜索(DFS)不局限于迷宫一类的问题,凡是这种有其实状态和目标状态的,往往都可以套用之前的模板,将上下左右改为电梯的上升和下降就可以了。
错误的代码
#include
using namespace std;
int a,b,n,ans=999999;
int skill[210];
int sign[210];
void dfs(int now,int step)
{
if(now==b) //判断是否到达目标的那一层,并记录步数
{
ans=min(step,ans);
return;
}
if(sign[now+skill[now]]==0&&now+skill[now]>0&&now+skill[now]<=n)//上升
{
sign[now+skill[now]]==1;//标记这一层来过了
dfs(now+skill[now],step+1);
sign[now+skill[now]]==0;//重置标记
}
if(sign[now-skill[now]]==0&&now-skill[now]>0&&now-skill[now]<=n)//下降
{
sign[now-skill[now]]==1;//标记这一层来过了
dfs(now-skill[now],step+1);
sign[now-skill[now]]==0;//重置标记
}
}
int main()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++)
cin>>skill[i];
dfs(a,0);
if(ans==999999) cout<<-1;
else cout< 为什么我说它是错误的代码呢?因为它没有AC,让你们看一下我光荣的战绩。
实际上,虽然深搜很简单,但是很多情况下不宜使用,因为递归涉及到爆栈的问题,如果你什么RE,什么MLE什么乱起八糟的,一般都是递归爆栈了,所以有必要使用广搜。
本题题解将在队列中呈现。
二、队列
1)核心思想
队列其实正如其名,就是排队吗,与栈(你们都这么强是吧,默认你们会了,不过不会也丝毫不影响阅读下文)不同的是,队列有两个关键点:队首和队尾。
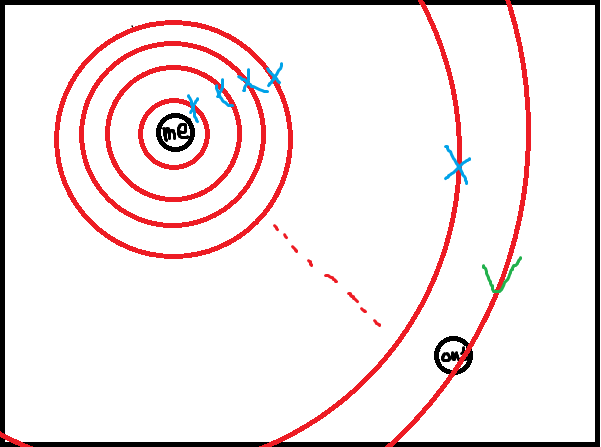
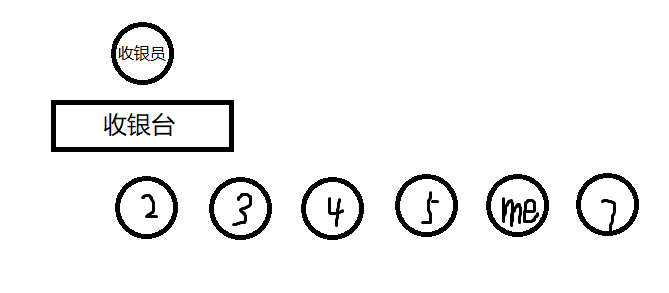
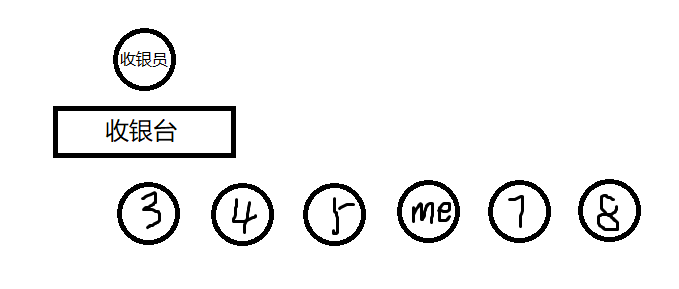
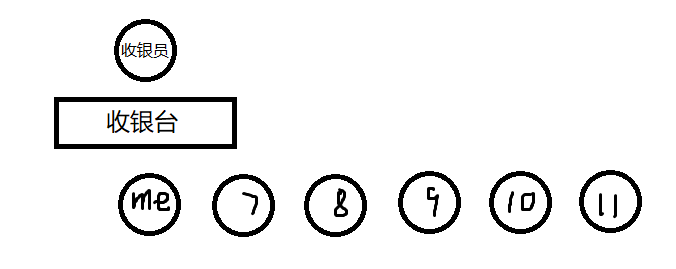
例如我要去买一份麻辣拌,那么在购买时一定是这样的:
然后……
……(繁琐的等待)
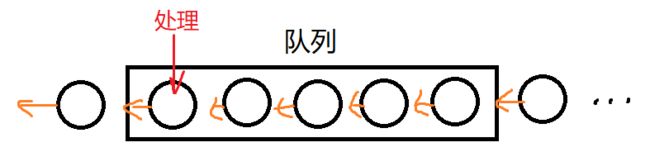
显然我们会发现收银员会优先处理在队首的人的订单,后来的人则插入队尾。
队列也是这样的处理模式,时刻处理队首元素,然后队首元素出队,新元素在队尾入队。
学到一个新的数据结构或算法,我们势必要考虑学习它的意义,它能解决什么样的问题。
2)广度优先搜索
这是运用队列最为标志性的一种算法,为什么广搜要用到队列呢?
显然,例如我们处于状态2时,对于状态2的处理,深搜会直接进行,而广搜会延后进行,先寻找状态3。
这样我们就不能直接想深搜一样递归了,但是这恰巧符合队列,从状态1扩展出状态2,3,4,5,这四个元素先入队,那么这四个元素就先处理,这样就解决了处理状态顺序的问题,然后再处理这四个子状态分别的子状态就可以了。
3)广度优先搜索的实现方法
- 1>手写实现,也就是根据原理自行实现
- 2>stl队列,本身C++里面是有专门的队列的,无需手写
主要懒得写,详细参见:我们延老师的博客
为了方便大家理解,实际上是我用惯手写的了,所以小编按照手写队列来说明。
4)例题
例1
刚才还留着一道没有说了,先搞完这个: https://www.luogu.com.cn/problem/P1135
P1135 奇怪的电梯
AC代码
#include
using namespace std;
struct node{
int now;//当前位置
int step;//到达这一位置的步数
}q[1000000];
int n,a,b,skill[210000],head=0,tail=1,ans=999999,mapp[100000];//head是队首指针,tail是队尾指针(此处指针不是语法的指针,而是一种比喻)
void bfs()
{
q[tail].now=a;
q[tail].step=0;//初始元素入队
while(tail>head)//判断队列内是否还有元素
{
head++;
int now=q[head].now;
int step=q[head].step;//队首出队
int now1,step1;
for(int i=1;i<=2;i++)
{
if(i==1) now1=now+skill[now];//上升
else now1=now-skill[now];//下降
step1=step+1;//走了这一步
if(now1>n||now1<1||mapp[now1]==1) continue;//判断新位置是否可行
q[++tail].now=now1;
q[tail].step=step1;//新元素入队
mapp[now1]=1;//标记走过此地
if(now1==b)//按照广搜的原理:先找近的再找远的,所以第一个找到的就是最优解,无需回溯
{
ans=step1;
break;
}
}
}
}
int main()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++)
cin>>skill[i];
if(a==b) cout<<0;
else
{
bfs();
if(ans==999999) cout<<-1;
else cout< 例2
题目链接:https://www.luogu.com.cn/problem/P1443
P1443 马的遍历
题目描述 输入格式 输出格式 输入输出样例 首先,这道题变了,不是迷宫那种上下左右的那种走法,所以对于每次扩展坐标的更改方法,需要改动; emmmmm,树好麻烦的,一上来就是无数个新的需要掌握的关键词,小编当年被整出心理阴影了。 首先,这是我们生活中常见的树该有的形状: 这是数据结构中树的形状: 倒不是不能像正常的生活中的树一样正放,但是还是图二在讲解中看的更方便。 最重要的几个术语 在树最顶端的节点叫做根节点; 每个节点又生出若干个子节点; 而这个节点又叫做这些子节点的父亲节点; 没有子节点的节点叫做叶子节点; 树的层次:从根节点开始算,根节点算第一层,如上图有3层; 树的高度:从叶子节点开始,自底向上增加; 树的深度:与树的深度相反,自顶向下增加; 二叉树与普通的树不同的是,二叉树是指每一个节点的子节点个数都小于等于2的树。 具体二叉树有什么特殊意义,在讲二叉排序树时再仔细讲。 对于树的存储,很麻烦;但是二叉树就不同了,它能确定每个节点的子节点的个数,那么我们可以用一个结构体来表示。 这样,在访问每一个节点的时候,就能快速知道其子节点的编号,并进入其左子树或右子树继续访问。 二叉树既然建立了,就要有什么查找,修改之类的操作,那么遍历就是最为基础的。 先说层序遍历,就是下面这一个二叉树,一共有四层: 那么就一层一层搜,从根节点开始由近到远,这像极了什么呢?广度优先搜索! 然后就是先序遍历、中序遍历、后序遍历了,其实他们的本质都是深度优先搜索。 所以说先、中、后其实就是指根节点的顺序。 就这个二叉树,代入进去之后顺序就是这样的: 其中我的完整代码如下: 什么也别说,敢在这一部分混得先做好心里准备,因为从这里开始,各种操作都上线了,代码量不仅大还不易查错,所以这里的东西尽量练出自己的模板并背会。 之前我们学了二叉树,但是二叉树“每一个节点的子节点个数都小于等于2的树”的定义貌似没有什么实际意义,但是在二叉排序树上,就能看出它的好处。 然后是3,3<8,放在左子树 这种方法有点类似于二分,查询次数不会超过树的深度,时间复杂度大约就是O(log n)。 题目链接:https://www.luogu.com.cn/problem/P5076 因为通常我们都会用到二分,代码量很少,但是一扯到树,代码量就上来了。 前言:事先说明一点,平衡树treap是二叉排序树的升级版,但在使用过程中有使用到随机数生成器,NOIP/CSP不能使用,所以小编会简要说明,不会贴上代码。此部分的作用在于为红黑树做铺垫。 首先,二叉排序树存在严重的缺陷。 左旋:将原根节点变成新左子树的节点,将原右子树节点变成新根节点 右旋:讲原根节点变成新右子树的节点,将原左子树节点变成新根节点 举个麻烦一点的例子: 先讲一下最小堆,就像摞东西一样,不过是一种树,这种树要求子节点的值都大于父节点的值。 首先,我们就像堆一样构建这棵树,随时保证这棵树的优先级的分布是最小堆。(反正这也没有什么原因,就是为了看起来更随机一点) 好了,我懒得配图了,一下图解来源于《信息学奥赛一本通(提高篇)》,此处致敬作者 4)删除 至于图解吗,就再次致敬作者吧: 好了,平衡树treap就到此位置吧。 未完待续…… 很多东西都是明摆着要用一棵树来维护的,但是树状数组正如其名,是为了优化暴力做法而构建的树,因为这样的数组就像树一样(其实就是树),因此得名。 直接上问题,要求:给出数列,支持单点加,求区间和 咱们先放个图,先看看它的样子。 其中最下面灰色,标注着A的是原数组,橙色的部分是另一个新开的数组,通常名称为C。 这种棘手的问题一定不会有十全十美的做法,既然现在要优化区间和,那么单点加就麻烦了。 只要找出前缀和后就能差分得到区间和,所以当务之急是求出前缀和。 不过由于区间的长度不一定是2的整数次幂,所以,i循环时一定要从大到小。 这已经是模板了,那么呈上完整代码: 其实树状数组的能力不局限于此,可以实现: (其中区间修改只支持可逆操作,例如加减乘除,但最大值最小值等不可以,否则无法查询) 处理一下上面没有解决的问题,最大最麻烦的问题有两个,一个是树状数组不支持不可逆操作,另一个是区间修改,区间查询。 这很简单的吧,只要找到叶子节点就把数列中对应的数插入进去就可以了。 那么这个东西就作为一个函数提出来: 于是这个建立过程就是这样的: 单点加太简单了,就不说了,不过区间加呢? 我就总想着很懒,下一次查询区间和一定不会查询到我的~~~ 这样就能得到区间加的代码了: 最终,标记会一直下放到叶子节点的子节点,即空白节点,空白的节点是永远不会访问到的,无需考虑。 查询部分就很简单了,直接呈上代码: 题目链接:https://www.luogu.com.cn/problem/P3372 划分树是线段树的升级版,比线段树要快一些。 未完待续……
有一个n*m的棋盘(1
一行四个数据,棋盘的大小和马的坐标
一个n*m的矩阵,代表马到达某个点最少要走几步(左对齐,宽5格,不能到达则输出-1)
输入 #1
3 3 1 1
输出 #1
0 3 2
3 -1 1
2 1 4解析
其次,这道题不同的是,没有一个确定的结束位置,深搜难以实现,而广搜就是单纯的由近到远,全搜一遍,所以此题适宜使用广搜。AC代码
#include三、树的基本知识
所以一些不怎么常用的,要么是懒的写,要么是懒得学,小编就不讲解了。
非要学的话,看百度吧:https://baike.baidu.com/item/%E6%A0%91/2699484?fr=aladdin
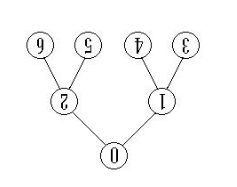
如图2所示,0节点是根节点,1是0的子节点,0是1的父亲节点,3,4,5,6都是叶子节点;
还有:
不过后续用树时小编懒得用这三个词,太高级,我不配使用……四、二叉树
1)定义
如果某一棵二叉树每一个节点(不包括叶子节点)都有左子树和右子树,那么则称这个二叉树为满二叉树。
例如
之前这个图二就是一个满二叉树。
但是这个就不是满二叉树:
2)二叉树的存储与建立
struct node{//定义每个节点的一些必要的信息
int left;//左子树编号
int right;//右子树编号
}tree[10000];
二叉树的建立,就不需要我多说了吧,直接代码呈上:void build()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x>>l>>r;
tree[x].left=l;
tree[x].right=r;
}
}
3)二叉树的遍历
对于二叉树的遍历,最常见的也就是以下几种:
只要一层一层放入队列里面,再一个一个扩展出子节点就可以了,但是层序遍历貌似不怎么常用,广搜的代码已经讲过了,所以小编就不提供代码了。
按照这个原理,写成代码:void first_order(int i)
{
if(i==0) return;
cout<
#include五、二叉排序树
1)引入
二叉排序树的原理很简单,就是把一堆数据放到一棵树中,起初树是空的,任一元素为树的根节点,然后不停的执行这样的操作:小于当前节点的放在左子树上,否则放在右子树上。
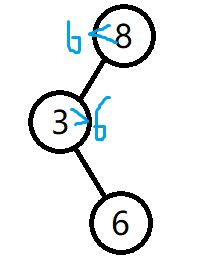
例如这串数据:8,3,6,5,10,12,9,13
首先,8为根节点
然后是6
……
这样查询的话只要从根节点开始一路比大小就可以了,比如我想知道9是否存在,9>8,所以访问根节点的右子树,9<10,所以访问10的左子树,9=9,说明9存在在这一串数中。
2)例题
P5076 【深基16.例7】普通二叉树(简化版)
恕小编无此能耐,如果后面改好了代码我会更新的,先看看别人的题解吧: 传送门
小编的代码不是MLE就是TLE,不知道哪里的问题,望大佬看到评论区留言。
#include早知道我就找个模板题了……
不过写了这么多代码,我才发现这道题没必要用二叉排序树……
看看人家的博客,AC的多轻松:https://www.luogu.com.cn/blog/yuan-xin/solution-p5076#3)为什么需要使用二叉排序树
二分和二叉排序树都要求数据有序,但是二分时刻要求数列有序,二叉排序树时刻要求树本身有序。
所以二分的缺点在于动态插入效率不高,每新插入一个数,就要重新排序一次,时间复杂度为O(n);
二叉排序树在插入一个数时,只要将这个节点找到正确位置插入就可以了,时间复杂度为O(log n)。六、改进型1:*平衡树Treap
1)引入
对于以下数据:
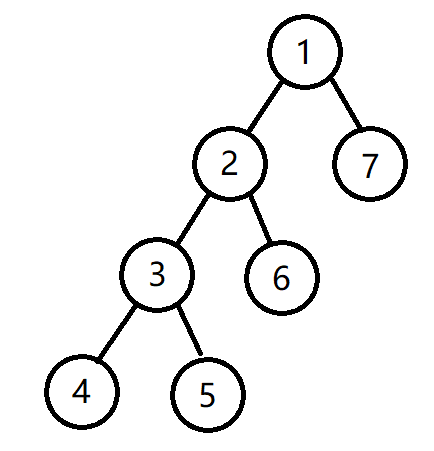
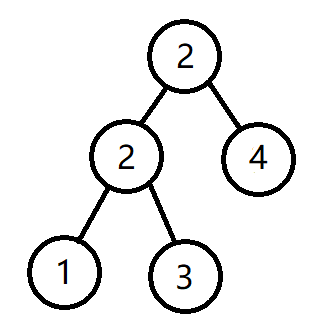
3,2,4,1,7,8,6,5
按顺序组成的二叉排序树长这样:
但是如果我是从小到大按顺序输入呢?:1,2,3,4,5,6,7,8
显然,按照顺序输入的二叉排序树会退化成链状,查询的时间复杂度就从O(log n)变成了O(n)。
辛辛苦苦多年写了不少代码建起来的代码,和人家直接for循环的时间复杂度一致,所以就得想办法改变一下。
比较一下之前两个图,第一个图是我很随机的打乱了这组数的顺序,所以树状结构很明显,而第二个图就是刻意输入的有序数据,那么说明:
数据的顺序越随机,二叉排序树就越不容易退化成链。
怎样做到随机呢?一定要把数组打乱,但为了防止链的情况尽量不发生,平衡树treap用到了
优先级这一方法,优先级是用随机数生成器随机生成的,每一个点都有自己的优先级。
平衡树有很多种,现在讨论的只是其中一种,但是凡是平衡树一般都要在插入时进行改变树结构的操作,以维持树的平衡,几乎都需要
左旋和
右旋这两种最重要的操作。
2)左旋&右旋
就这棵树,右旋一下:
首先如图所示挪位置:
然后左子树的地方把左子树的左子树补上去:
左子树的右子树补到右子树的左子树;
和根的右子树补到右子树的右子树:
多试几次,就会发现这个移法一定在操作后这棵树仍是一棵二叉排序树。
因此,左旋和右旋都不会改变这棵树本质是二叉排序树这一事实。
听起来感觉很麻烦,其实代码很简单,
小编懒得整了,自己去搜吧,反正noip也不能用。
3)插入
例如:
那么具体方法如下:
当我们遇到一个节点想要删除它的时候,我们需要考虑实际情况,其实归纳下来只有这三种:
七、改进型2:红黑树
先看一篇很敷衍的吧:传送门八、树状数组
1)引入
只有单点加不难,O(1)就可以了
只求区间和也不难,用前缀和查分一下就ok了,照样O(1)
但是两个如果放在一起就不能用前缀和了,单点加照样O(1),但是区间和就变成了O(n),当询问次数多了的时候就超时了……
所以我们就请出了树状数组。2)核心原理
虽然是一个一个橙条,但是其实是每一个节点保存着对应橙条内的区间和(每个节点的编号为区间的结束编号,仔细观察,就会发现各区间的结束位置编号都各不相同),并且只靠橙条,就可以拼出区间内任意数的前缀和,例如随便找个数:7,对应的就是下面三部分:
将这三个值拼起来,就是这一前缀和。
3)单点加
原来只需要加一次,加在原数组上,但是现在需要修改log n次,例如我要修改a[1],那么我就要一路扶摇直上,因为上面的区间和也需要刷新:
看到这里,觉得很麻烦吗?不代码很简单,因为任何数都可以分解为的形式,例如还是a[1],那么它需要修改的区间长度很直观,分别是:
...
1需要加的区间长度很容易看出来在不停乘以2,但是其他的显然不完全符合,例如3。
渐渐地,我们会发现一个规律:设我们现在在n号节点所代表的区间,下一次区间增加的长度就是,这个大小记为lowbit(n),例如3吧,二进制下是,那么lowbit(n)=,(以下二进制忽略下标2和括号,
原因:懒得写,好麻烦)然后,11+1=100,十进制表示数为4,接着lowbit(4)=100,100+100=1000,十进制为8,然后……
所以这个顺序就是3=>4=>8=>16,恰好和图上是一致的。
接下来的问题:lowbit怎么求?听好,
前方高能
假设要求lowbit的这个数是x,假设x最小的一位1是在第k位,那么对x取反,此时:k+1位及之前全部1变0,0变1,第k位变成了0,第k-1位及以后全部0变1;此时再+1,k+1位及之前不变,第k-1位及以后所有1遇见加的1不断进位至第k位,第k位由于进位变成了1。整个操作过程数学语言为:~x+1。
用这玩意去&x,就会发现k+1位及之前恰好相反(因为之前有过取反操作),于是抵消全部为0;第k-1位及以后两者全部是0,于是这一部分也全是0;只有第k位,x中是1,~x+1中也是1,&运算后这一位就是1,再看其它位,全部是0,于是这个1就提出来了,表示成10进制的值就已经是2的次幂。
在二进制补码中,~x+1写作-x。
于是:lowbit(x)=x&-x 。
于是就有了超级简洁的代码实现
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=y;
}
4)前缀和
根据单点的方法,同理就有前缀和的求法:int pre(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=c[i];
return ans;
}
5)上例题
P3374 【模板】树状数组 1
AC代码
#include
但是剩下没讲的两种实现起来都很麻烦,不过我们可以使用线段树。九、线段树
1)核心思想
先放个图(这是特殊情况下的线段树):
显然,这棵树的存储更占空间,树状数组只需要开n那么大,但是线段树通常要开到4×n。
对于各节点的编号,由于线段树的原理是分治,所以线段树是
完全二叉树,不懂的去看看百度吧: 传送门
可以把完全二叉树当作满二叉树,把不存在的节点当作不留信息的空节点,此时满足左子节点编号=当前节点
2,右子节点编号=当前节点2+1,尽管浪费了很多编号,但是这样能快速准确地找到某个节点的左子节点和右子节点。
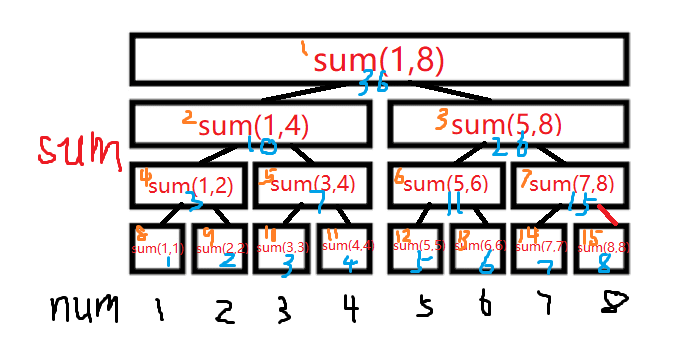
我们约定sum(l,r)表示数列num区间[l,r]的区间和/区间最小值/最大值等(线段树支持不可逆操作),此处及以后以区间和为例。
那么每一个节点的信息分别是:
其中:红色代表这个节点是怎么算的,蓝色代表该节点的准确值,黄色代表该节点编号。
由此可见:线段树的规律就是,根节点的值=左子节点的值(任意操作,例如:+,max,min等)右子节点的值。
2)建立
不过,有一个频繁使用的操作就是在回溯的过程中更新根节点的值,因为我们是先知道叶子节点的值的,然后再向上更新。
void pushup(int i) {sum[i]=sum[i*2]+sum[i*2+1];}
void build(int i,int l,int r)
{
if(l==r)
{
sum[i]=num[l];
return;
}
int mid=(l+r)/2;
build(i*2,l,mid);
build(i*2+1,mid+1,r);
pushup(i);
}
3)区间加
难道是要遍历一遍区间,然后不断单点加吗?这样的时间复杂度还不如暴力解决。
我们只能找其他办法解决这个问题————懒!
整个程序当然有大量节点等待更新信息,我们的一致处理方法就是能不更新就不更新,非要更新的时候把多年来没有更新的一次性全部更新了。
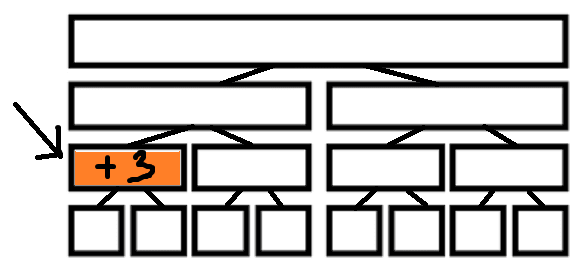
怎样能尽量不更新呢,那么当然是打标记(可以称之为懒标记),比如说我要给这个节点所代表的区间整个加3:
于是我停止向下继续让子树内各节点区间加3,打个标记:+3,记录一下我身上的任务sum[i]=3*区间长度。
这时,假如这个节点很不幸,正好在区间查询或区间加发现它懒到没有让子树的节点们增加,就要赶在没有发生什么错误之前,标记下放:
void pushdown(int i,int l,int r)
{
if(tag[i])//tag用来标记
{
int mid=(l+r)/2;
tag[i*2]+=tag[i];//同一个节点只要不被调用,就可以一直被标记,所以不是赋值,而是+=
sum[i*2]+=(long long)(tag[i]*(mid-l+1));//让左子节点处理这件事
tag[i*2+1]+=tag[i];
sum[i*2+1]+=(long long)(tag[i]*(r-mid));//让右子节点处理这件事
tag[i]=0;//然后自己又是一个干净的结点啦,无官一身轻
}
}
void update(int i,int l,int r,int L,int R,int x)
{
if(l>=L&&r<=R)//当当前区间正好在给定区间内时
{
tag[i]+=x;//放个懒标记
sum[i]+=(long long)(x*(r-l+1));//再暂时处理一下自己的信息
return;//然后就罢工了
}
pushdown(i,l,r);//若正好路过,以后需要调用到当前这个点的子树的信息,那么立刻标记下放
int mid=(l+r)/2;
if(mid>=L) update(i*2,l,mid,L,R,x);
if(mid4)区间查询
long long query(int i,int l,int r,int L,int R)
{
if(l>=L&&r<=R) return sum[i]; //叶子节点直接返回
int mid=(l+r)/2;
long long ans=0;//有时可能返回值很大,建议用long long
pushdown(i,l,r);//标记下放
if(mid>=L) ans+=query(i*2,l,mid,L,R);
if(mid5)例题
P3372 【模板】线段树 1
AC代码
#include6)划分树
传送门十、基础图论
不过你可以在这里寻宝:传送门
这是我曾经写过的有关图的博客。