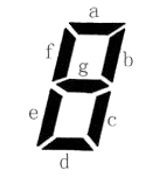第十一届蓝桥杯大赛软件类省赛第二场 C/C++ 大学 B 组

试题 A: 门牌制作 本题总分：5 分

【问题描述】
小蓝要为一条街的住户制作门牌号。 这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。 小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字 符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、0、1、7，即需要 1 个 字符 0，2 个字符 1，1 个字符 7。 请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

题解

直接手推，100以内个位数有10个2，十位数有10个2，所以100以内共有20个2；1000以内有10个100，所以有1020=200个2，在百位上有100个2，所以1000以内共有300个2；2000以内有2个1000，所以有2300个2，共有600个2；2020以内有21个千位的2以及1个十位的2和2个个位上的2，共24个2；综上，一共有624个2。

代码

略

---

试题 B: 既约分数 本题总分：5 分

【问题描述】
如果一个分数的分子和分母的最大公约数是 1，这个分数称为既约分数。 例如，$\frac{3}{4},\frac{5}{2},\frac{1}{8},\frac{7}{1}$ 都是既约分数。 请问，有多少个既约分数，分子和分母都是 1 到 2020 之间的整数（包括 1 和 2020）？
【答案提交】
这是一道结果填空题，你只需要算出结果后提交即可。本题的结果为一个 整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

题解

数据不大，直接枚举并求GCD统计合法的方案即可。

答案：2481215

代码

#include 

using namespace std;

int gcd(int a, int b) {
     
	if (b == 0) return a;
	return gcd(b, a%b);
}

int main() {
     
	int ans = 0;
	for (int i = 1; i <= 2020; i++) {
     
		for (int j = 1; j <= 2020; j++) {
     
			if (gcd(i, j) == 1) {
     
				ans ++;
			}
		}
	}
  printf("%d\n", ans);
  return 0;
}

---

试题 C: 蛇形填数 本题总分：10 分

【问题描述】
如下图所示，小明用从 1 开始的正整数“蛇形”填充无限大的矩阵。

容易看出矩阵第二行第二列中的数是 5。请你计算矩阵中第 20 行第 20 列 的数是多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

题解

直接模拟，可以利用每条直线内的点截距相同，相邻的直线截距差1的特征进行模拟；

找规律会快点，对于处在对角线的点所在的左上三角的边长为 $2(n-1)+1$，即 $2n-1$。我们把这个上三角的规模为 $Sn=\frac{t(t+1)}{2}$，其中，$t=2n-1$。我们计算前 $t-1$ 层的规模，然后加上第 $t$ 层的规模的一半上取整即可，上取整的原因是对角线层一定为奇数。
$$s1=\frac{38\ast (38+1)}{2}=741，s2=\lceil \frac{39}{2}\rceil =20，ans=s1+s2=761$$

答案：761

代码

略

---

试题 D: 跑步锻炼 本题总分：10 分

【问题描述】
小蓝每天都锻炼身体。 正常情况下，小蓝每天跑 1 千米。如果某天是周一或者月初（1 日），为了 激励自己，小蓝要跑 2 千米。如果同时是周一或月初，小蓝也是跑 2 千米。 小蓝跑步已经坚持了很长时间，从 2000 年 1 月 1 日周六（含）到 2020 年 10 月 1 日周四（含）。请问这段时间小蓝总共跑步多少千米？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

题解

模拟即可，注意闰年的情况。

答案：8879

代码

#include 

using namespace std;

int month[13] = {
     0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int main() {
     
  int y = 2000, m = 1, d = 1, w = 6, ans = 0;
  while(true) {
     
    ans += (d == 1 || w == 1) + 1;
    if (y == 2020 && m == 10 && d == 1) {
     
			break;
		}
    w = (w + 1) % 7;
    d = d + 1;
    if((y % 400 == 0 || y % 4 == 0 && y % 100 != 0) && m == 2) {
     
    	if (d > month[m] + 1) {
     
				d = 1;
				m += 1;
			}
    } else if (d > month[m]) {
     
			d = 1;
      m += 1;
		}
    if(m == 13) {
     
      y += 1;
      m = 1;
    }
  }
  printf("%d\n", ans);
	return 0;
}

---

试题 E: 七段码 本题总分：15 分

【问题描述】
小蓝要用七段码数码管来表示一种特殊的文字。

上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二 极管，分别标记为 a, b, c, d, e, f, g。 小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符 的表达时，要求所有发光的二极管是连成一片的。 例如：b 发光，其他二极管不发光可以用来表达一种字符。 例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上 一行的方案可以用来表示不同的字符，尽管看上去比较相似。 例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。 例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光 的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

题解

枚举子集，一共有 $2^7$ 种方案。当方案中联通块大于等于2时，非法。判断联通块可以用并查集或者dfs。建图的时候可以根据 7 管码的邻接情况建邻接矩阵或邻接表。

答案：80

代码

#include 

using namespace std;

int G[8][8], vis[8];
int pack[8], sz;
int ans;

void init() {
     
	G[1][2] = 1; G[1][6] = 1;
	G[2][3] = 1; G[2][7] = 1;
	G[3][4] = 1; G[3][7] = 1;
	G[4][5] = 1;
	G[5][6] = 1; G[5][7] = 1;
	G[6][7] = 1;

	for (int i = 1; i <= 7; i++) {
     
		for (int j = 1; j <= i; j++) {
     
			G[i][j] = G[j][i];
		}
	}
}

void dfs1(int u) {
     
	vis[u] = 0;
	for (int i = 1; i <= 7; i++) {
     
		if (i != u && G[u][i] == 1 && vis[i] == 1) {
     
			dfs1(i);
		}
	}
}

void dfs2(int index) {
      //枚举子集
	if (index == 8) {
     
		if (sz > 0) {
     
			dfs1(pack[1]); //处理连通块
			int flag = 1;
			for (int i = 1; i <= sz; i++) {
     
				if (vis[pack[i]] == 1) {
     
					flag = 0;
				} else {
     
					vis[pack[i]] = 1; //还原
				}
			}
			if (flag == 1) {
     
				ans ++;
			}
		}
		return ;
	}
	vis[index] = 1;
	pack[++sz] = index;
	dfs2(index + 1);
	vis[index] = 0;
	--sz;
 	dfs2(index + 1);
	return ;
}

int main() {
     
	init();
	dfs2(1);
	printf("%d\n", ans);
	return 0;
}

---

试题 F: 成绩统计 时间限制: 1.0s 内存限制: 256.0MB 本题总分：15 分

【问题描述】
小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是 一个 0 到 100 的整数。 如果得分至少是 60 分，则称为及格。如果得分至少为 85 分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整
数。
【输入格式】
输入的第一行包含一个整数 n，表示考试人数。 接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。
【输出格式】
输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分 四舍五入保留整数。
【样例输入】
7
80
92
56
74
88
100
0
【样例输出】
71%
43%
【评测用例规模与约定】
对于 50% 的评测用例，1≤n≤100。 对于所有评测用例，1≤n≤10000。

题解

简单题，先统计及格和优秀的人数，再计算相应的比例，注意四舍五入以及百分比的条件。还有就是优秀一定及格。

代码

#include 

using namespace std;

int main() {
     
	int n, pass = 0, excellent = 0;
	int score;
	double ans1, ans2;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
     
		scanf("%d", &score);
		if (score >= 85) {
     
			pass ++;
			excellent ++;
		} else if (score >= 60) {
     
			pass ++;
		}
	}
	ans1 = (100.0*pass/n+0.5);
	ans2 = (100.0*excellent/n+0.5);
	printf("%d%%\n%d%%\n", (int)ans1, (int)ans2);
	return 0;
}

---

试题 G: 回文日期 时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
2020 年春节期间，有一个特殊的日期引起了大家的注意：2020 年 2 月 2 日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202， 恰好是一个回文数。我们称这样的日期是回文日期。 有人表示 20200202 是 “千年一遇” 的特殊日子。对此小明很不认同，因为 不到 2 年之后就是下一个回文日期：20211202 即 2021 年 12 月 2 日。 也有人表示 20200202 并不仅仅是一个回文日期，还是一个 ABABBABA 型的回文日期。对此小明也不认同，因为大约 100 年后就能遇到下一个 ABABBABA 型的回文日期：21211212 即 2121 年 12 月 12 日。算不上 “千 年一遇”，顶多算 “千年两遇”。 给定一个 8 位数的日期，请你计算该日期之后下一个回文日期和下一个 ABABBABA 型的回文日期各是哪一天。
【输入格式】
输入包含一个八位整数 N，表示日期。
【输出格式】
输出两行，每行 1 个八位数。第一行表示下一个回文日期，第二行表示下 一个 ABABBABA 型的回文日期。
【样例输入】
20200202
【样例输出】
20211202
21211212
【评测用例规模与约定】
对于所有评测用例，10000101 ≤ N ≤ 89991231，保证 N 是一个合法日期的 8 位数表示。

题解

两种思路，第一种，直接模拟日期递增，然后再判断该日期是否为回文串，找到最近日期即可。直观地感觉日期地规模为 $8\ast 10^7$，但题目有提示规模在一千以内，所以放心模拟即可。

这里主要讲第二种，由于题目输出提示，我们可以得到年份一定为四位数，所以把所有可能的年份枚举处理，规模是 $10^4$ 。年份一出来，日期就已固定，然后把非法日期筛掉。最后去找最近的日期即可。注意，这里回文的类型有两种，分别存到不同的表中即可，当然 『ABABBABA』型是回文的子集。

这里似乎有个坑点，当 n 是最后一个 8 位的 ABABBABA 日期或者最后一个回文日期怎么办？不要怕，注意：10000101 ≤ N ≤ 89991231，所以两个答案均有解。

代码

#include 

using namespace std;

const int N = (int)1e4+5;

int month[13] = {
     0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

struct node {
     
	int y, m, d;
	bool operator < (const node& B) const{
     
		if (y == B.y) {
     
			if (m == B.m) return d < B.d;
			return m < B.m;
		}
		return y < B.y;
	}
	
	bool operator == (const node& B) const{
     
		return y == B.y && m == B.m && d == B.d;
	}
	
}tab1[N], tab2[N];

int n1, n2; //合法回文日期和ABABBABA回文的规模

//判断日期是否合法
bool judge(node& d) {
     
  if (d.m < 1 || d.m > 12) return false;
	int mlimit = month[d.m];
	if (d.m == 2 && (d.y % 400 == 0 || d.y % 4 ==0 && d.y % 100 != 0)) mlimit ++; //闰年
	if (d.d < 1 || d.d > mlimit) return false;
  return true;
}

int main() {
     
	int idx;
	char str[8];
	node in, cur;
	scanf("%s", str);
	in.y = (str[0]-'0')*1000+(str[1]-'0')*100+(str[2]-'0')*10+(str[3]-'0');
	in.m = (str[4]-'0')*10+(str[5]-'0');
	in.d = (str[6]-'0')*10+(str[7]-'0');
	n1 = n2 = 0;
	
	for (int i = 0; i < 10; i++) {
     
		for (int j = 0; j < 10; j++) {
     
			cur.y = i*1000+j*100+i*10+j;
			cur.m = cur.d = j*10+i;
			if (judge(cur)) tab2[n2++] = cur;
			for (int z = 0; z < 10; z++) {
     
				for (int k = 0; k < 10; k++) {
     
					cur.y = i*1000+j*100+z*10+k;
					cur.m = k*10+z; cur.d = j*10+i;
					if (judge(cur)) tab1[n1++] = cur;
				}
			}
		}
	}
	
	sort(tab1, tab1+n1);
	sort(tab2, tab2+n2);
	
	for (int i = 0; i < n1; i++) {
     
		if (tab1[i] == in) {
     
			printf("%d%d%d%d%d%d%d%d\n",
				tab1[i+1].y/1000,
				tab1[i+1].y/100 % 10,
				tab1[i+1].y/10 % 10,
				tab1[i+1].y % 10,
				tab1[i+1].m/10,
				tab1[i+1].m % 10,
				tab1[i+1].d/10,
				tab1[i+1].d % 10);
			break;
		}
	}
	for (int i = 0; i < n2; i++) {
     
		if (tab2[i] == in) {
     
			printf("%d%d%d%d%d%d%d%d\n",
				tab2[i+1].y/1000,
				tab2[i+1].y/100 % 10,
				tab2[i+1].y/10 % 10,
				tab2[i+1].y % 10,
				tab2[i+1].m/10,
				tab2[i+1].m % 10,
				tab2[i+1].d/10,
				tab2[i+1].d % 10);
			break;
		}
	}
	return 0;
}

---

试题 H: 子串分值和 时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
对于一个字符串 S，我们定义 S 的分值 f(S) 为 S 中出现的不同的字符个 数。例如 f(”aba”) = 2，f(”abc”) = 3, f(”aaa”) = 1。 现在给定一个字符串 S[0…n−1]（长度为 n），请你计算对于所有 S 的非空 子串 S[i…j](0≤i≤ j < n)，f(S[i…j]) 的和是多少。
【输入格式】
输入一行包含一个由小写字母组成的字符串 S。
【输出格式】
输出一个整数表示答案。
【样例输入】
ababc
【样例输出】
28
【评测用例规模与约定】
对于 20% 的评测用例，1≤n≤10； 对于 40% 的评测用例，1≤n≤100； 对于 50% 的评测用例，1≤n≤1000； 对于 60% 的评测用例，1≤n≤10000； 对于所有评测用例，1≤n≤100000。

【样例说明】

子串	f值
a	1
ab	2
aba	2
abab	2
ababc	3
b	1
ba	2
bab	2
babc	3
a	1
ab	2
abc	3
b	1
bc	2
c	1

题解

求 $\frac{n(n+1)}{2}$ 个非空子区间的区间种类数之和，直接枚举区间端点后计算区间种类数复杂度会比较高。我们换种思路，直接计算每个点对于它存在区间的贡献。对于一个区间多个相同的数字，其贡献归为第一个出现的数字或者最后一个出现的数字，如果是前者则要维护一个类似 序列自动机 中的索引数组，用来得到当前数字前缀中该数字只出现 1 次的区间长度，记为 prenum ；包括该前缀区间任意后缀的串的种类就可以直接计算出来，这是个分步乘法，后缀串的长度为 n-idx+1，记为 sufnum。综上，每个点的贡献我们就可以 $O(1)$ 时间内计算出来，所以总的复杂度为 $O(n)$。如果维护后缀第一次出现的位置则同理。

• 极限大小计算：
  $$ans=\sum _{i=1}^{n}i\ast (n-i+1)=n\ast \sum _{i=1}^{n}i-\sum _{i=1}^n{i}^2+\sum _{i=1}^{n}i=\frac{n(n+1)(n+2)}{6}$$

注意，根据这个算式我们可以得出答案量级在 $10^{15}$，所以用长整型存储足够。

代码

#include 

using namespace std;

const int N = (int)1e5 + 5;

char str[N];

int next[26]; //前索引

int main() {
     
	int n;
	long long ans = 0;
  scanf("%s", str);
  n = strlen(str);
	memset(next, -1, sizeof next);
  for(int i = 0; i < n; i++) {
     
      ans += 1LL * (i - next[str[i] - 'a']) * (n - i);
      next[str[i] - 'a'] = i;
  }
  printf("%lld\n", ans);
  return 0;
}

拓展

1. 多次查询的区间种类数：经典区间计数问题，用两次树状数组或者主席树就可以离线解决
2. 因为一开始审题有误，看出区间如果一种字母出现多于 1 次，则不造成贡献。如果设问是这样的话还要预处理一个后缀第一次出现该数字的位置，答案就是：
   $$ans=\sum _{i=1}^n(i-pre\_index(val(i)))\ast (suf\_index(val(i))-i+1)$$

---

试题 I: 平面切分 时间限制: 1.0s 内存限制: 256.0MB 本题总分：25 分

【问题描述】
平面上有 N 条直线，其中第 i 条直线是 y = Ai ·x + Bi。 请计算这些直线将平面分成了几个部分。
【输入格式】
第一行包含一个整数 N。 以下 N 行，每行包含两个整数 Ai,Bi。
【输出格式】
一个整数代表答案。
【样例输入】
3
1 1
2 2
3 3
【样例输出】
6
【评测用例规模与约定】
对于 50% 的评测用例，1≤ N ≤4, −10≤ Ai,Bi ≤10。 对于所有评测用例，1≤ N ≤1000, −100000≤ Ai,Bi ≤100000。

题解

观察结果，我们发现这样一个规律，每次添加一条新的直线进来，一定会多一个平面。如果与之前的直线产生一个新的交点，则又会多出一个平面出来，如果多两个交点则多两个平面，以此类推。故当新增一条直线则产生的新的平面数为 ：新增的交点数 + 1。这里的 1 可以理解为和无限远的一个边界所围成的。综上，总的平面数就是依次添加多条线的交点变化情况。当然，我们需要预先做一个去重的操作，因为两条重合的直线只能算一条。

对于新增的一条直线最多会产生当前的直线数 - 1 个交点，所以如果纯暴力操作地话则时间复杂度为 $O(n^3)$，显然会超时，我们可以对于交点的维护搞一个 set 集合优化。时间复杂度将为 $O(n^{2}logn)$，临界情况则只会到达 $1e7$ 。

在判断交点的时候，为了避免浮点数带来的误差，直接记分子和分母，但这样判断大小的时候可能会乘爆 int ，用 long long 存一下即可，根据交点范围显然不会乘爆 long long。

代码

#include 

using namespace std;

const int N = (int)1e3 + 5;

struct line {
     
	int A, B;
	bool operator < (const line& V) const{
     
		if (A == V.A) {
     
			return B < V.B;
		}
		return A < V.A;
	}
	bool operator == (const line& V) {
     
		return A == V.A && B == V.B;
	}
}arr[N];

struct ver {
     
	//x = (B2-B1)/(A1-A2)
	//y = A1x+B1
	int B2, B1;
	int A1, A2;
	
	bool operator < (const ver& V) const{
      //左下到右上
		if (1ll*(B2-B1)*(V.A1-V.A2)==1ll*(V.B2-V.B1)*(A1-A2)) {
      //x1==x2
			//y1 < y2
			if (1ll*(V.A1-V.A2)*(A1-A2) > 0ll)
				return 1ll*(A1*B2-A2*B1)*(V.A1-V.A2) < 1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2);
			else
				return 1ll*(A1*B2-A2*B1)*(V.A1-V.A2) > 1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2);
		} else {
     
			//x1
			if (1ll*(V.A1-V.A2)*(A1-A2)>0ll)
				return 1ll*(B2-B1)*(V.A1-V.A2) < 1ll*(V.B2-V.B1)*(A1-A2);
			else
				return 1ll*(B2-B1)*(V.A1-V.A2) > 1ll*(V.B2-V.B1)*(A1-A2);
		}
	}
	/*
	bool operator == (const ver& V) {
		if (1ll*(B2-B1)*(V.A1-V.A2)==1ll*(V.B2-V.B1)*(A1-A2) &&
				1ll*(A1*B2-A2*B1)*(V.A1-V.A2)==1ll*(V.A1*V.B2-V.A2*V.B1)*(A1-A2))
				return true;
		return false;
	}
	*/
};

int n, cn; //原始线的数目 去重线数的目
long long ans = 2;
set<ver> s;

int main() {
     
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
     
		scanf("%d%d", &arr[i].A, &arr[i].B);
	}

	sort(arr, arr+n);

	cn = 1;
	for (int i = 1; i < n; i++) {
      //去重
		if (arr[cn - 1] == arr[i]) continue;
		if (cn != i) arr[cn] = arr[i];
		cn ++;
	}
	
	ver cur;
	for(int i = 1; i < cn; i++) {
     
		s.clear();
		for (int j = 0; j < i; j++) {
     
			if (arr[i].A == arr[j].A) continue; //平行
			cur.A1 = arr[i].A; cur.B1 = arr[i].B;
			cur.A2 = arr[j].A; cur.B2 = arr[j].B;
      		if (!s.count(cur)) s.insert(cur); //出现新的交点
		}
		ans += s.size() + 1;
	}
	
	printf("%lld\n", ans);
  return 0;
}

---

试题 J: 字串排序 时间限制: 1.0s 内存限制: 256.0MB 本题总分：25 分

【问题描述】
小蓝最近学习了一些排序算法，其中冒泡排序让他印象深刻。
在冒泡排序中，每次只能交换相邻的两个元素。
小蓝发现，如果对一个字符串中的字符排序，只允许交换相邻的两个字符， 则在所有可能的排序方案中，冒泡排序的总交换次数是最少的。 例如，对于字符串 lan 排序，只需要 1 次交换。对于字符串 qiao 排序， 总共需要 4 次交换。 小蓝的幸运数字是 V，他想找到一个只包含小写英文字母的字符串，对这 个串中的字符进行冒泡排序，正好需要 V 次交换。请帮助小蓝找一个这样的字 符串。如果可能找到多个，请告诉小蓝最短的那个。如果最短的仍然有多个， 请告诉小蓝字典序最小的那个。请注意字符串中可以包含相同的字符。
【输入格式】
输入一行包含一个整数 V，为小蓝的幸运数字。
【输出格式】
输出一个字符串，为所求的答案。
【样例输入】
4
【样例输出】
bbaa
【样例输入】
100
【样例输出】
jihgfeeddccbbaa
【评测用例规模与约定】
对于 30% 的评测用例，1≤V ≤20。 对于 50% 的评测用例，1≤V ≤100。 对于所有评测用例，1≤V ≤10000。

题解

由于限定的的合法字符只有 26 个字母，假设没有这个约束可以直接按完全逆序排序使得长度最小，然后在消去部分逆序数。而对于这题，首先字母是可以重复的，并且在长度相同若要保证字典序更小显然要让较大的字母数量较少，此时只要让较小的字母较多即可。

这里可能会陷入一个可贪心的思维误区：这也是我下面展示的一个假算法的例子：错误点在字典序最优是一个全局的特性，局部字典序最优不能保证全局字典序最优，所以正解应该是搜索+剪枝。

代码

假算法：

#include 

using namespace std;

const int N = (int)1e4+5;

int num[N];

int main() {
     
	int n, m;
	int _max, id, len, sum;
	scanf("%d", &n);
	
	sum = 0; len = 0;
	while (sum < n) {
     
		id = 1;
		for (int i = 2; i <= 26; i++) {
      //找到s最小的点, 如果存在多个取字典序更小的
      if (num[i] < num[id]) id = i;
		}
		sum = sum + len - num[id];
		len ++;
		num[id] ++;
	}
	
	m = sum - n; //注意更新逆序数差值
	for (int i = 1; i <= 26; i++) {
     
		if (num[i]) {
     
			_max = i;
		}
	}
	
	for (int i = _max; i >= 1; i--) {
     
		for (int j = 0; j < num[i]; j++) {
     
			printf("%c", 'a'+i-1);
		}
	}
	printf("\n");
	
	for (int i = 1; i <= m; i++) {
     
		/*
		//尽量消去最大的数字，并且逆序数变化得最少，如果变化量相同则选择字典序较小的方案
		id = 0; sum = INT_MAX;
		for (int j = 1; j <= 26; j++) {
			if (m - i + num[_max] - num[j] >= 0) {
				if (sum > num[j] - num[_max] + 1) {
					sum = num[j] - num[_max] + 1;
					id = j;
				}
			}
		}
		if (id) {
			num[id] ++;
			num[_max] --;
			if (!num[_max]) _max--;
			i += sum - 1;
			printf("~%d\n", id);
			continue;
		}
		*/
		
		for (int j = _max; j >= 1; j--) {
     
			id = 0;
			while(num[++id]!= num[j]);
			if (id != j) {
     
				num[id] ++;
				num[j] --;
				break;
			}
		}

		if (!num[_max]) {
     
			_max--;
		}
	}
	
	for (int i = _max; i >= 1; i--) {
     
		for (int j = 0; j < num[i]; j++) {
     
			printf("%c", 'a'+i-1);
		}
	}
	printf("\n");
  return 0;
}

搜索+剪枝

#include 

using namespace std;

const int N = (int)1e4+5;

int num[N], res[N];
int n, m, _max, len;

bool judge(int letter) {
     
	int i = 26, j = letter;
	while (!res[i]) i--;
	if (i == j) {
     
		while (i > 0 && j > 0) {
     
			if (res[i] != num[j]) {
     
				return res[i] > num[j];
			} else {
     
				i--; j--;
			}
		}
	}
	return i > j;
}

void dfs(int letter, int curlen, int cursum, int l) {
     
	if (cursum > n) return ;
	if (letter > _max) return ;
	if (curlen > len) return ;
	
	if (curlen == len && cursum != n) return ;
	if (letter == _max && cursum != n) return ;
	
	if (cursum == n) {
     
		if (curlen < len || judge(letter)) {
      //长度减小或字典序减小更新结果
			len = curlen;
			for (int i = 1; i <= 26; i++) {
     
				res[i] = num[i];
			}
		}
		return ;
	}

	for (int i = 1; i <= l; i++) {
     
		num[letter + 1] = i;
		dfs(letter + 1, curlen + i, cursum + i * curlen, i);
	}
	num[letter + 1] = 0;
}

int main() {
     
	
	scanf("%d", &n);

	m = 0; len = 0;
	while (m < n) {
     
		int id = 1;
		for (int i = 2; i <= 26; i++) {
      //找到s最小的点, 如果存在多个取字典序更小的
      if (res[i] < res[id]) id = i;
		}
		m += len - res[id];
		_max = max(_max, id);
		len ++; res[id] ++;
	}
	
	dfs(0, 0, 0, 10);
	
	for (int i = _max; i >= 1; i--) {
     
		for (int j = res[i]; j > 0; j--) {
     
			printf("%c", i-1+'a');
		}
	}
	printf("\n");

  return 0;
}