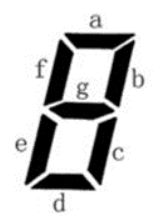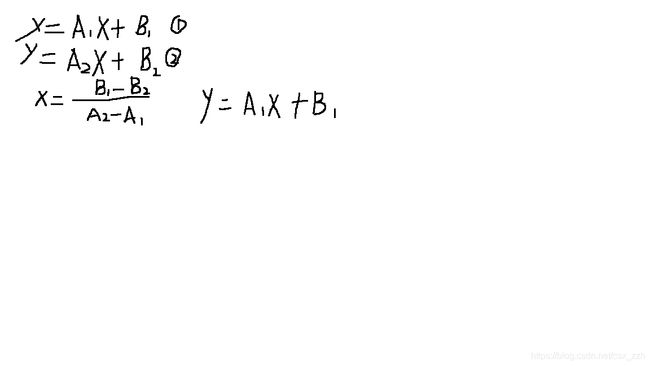2020第十一届蓝桥杯C/C++ B组省赛

结果填空题

试题A 门牌制作

【问题描述】
小蓝要为一条街的住户制作门牌号。
这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。
小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字
符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、 0、 1、 7，即需要 1 个
字符 0， 2 个字符 1， 1 个字符 7。
请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？

#include 
int main()
{
     
	int res=0;
	for(int i=1;i<=2020;i++)
	{
     
		int x=i;
		while(x)
		{
     
			if(x%10==2)  res++;
			x/=10;
		}
	}
	printf("%d\n",res);
}

/*
答案:  624
*/

试题B 既约分数

【问题描述】
如果一个分数的分子和分母的最大公约数是1，这个分数称为既约分数。例如，3/4 , 5/2 , 1/8 , 7/1都是既约分数。请问，有多少个既约分数，分子和分母都是1 到2020 之间的整数（包括1和2020）？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#include 
int gcd(int a,int b)
{
     
	if(b==0) return a;
	return gcd(b,a%b);
}
int main()
{
     
	int res=0;
	for(int i=1;i<=2020;i++)
	{
     
		for(int j=1;j<=2020;j++)
		{
     
			if(gcd(i,j)==1) res++;
		}
	}
	printf("%d\n",res);
}

/*
答案: 2481215
*/

试题C 蛇形填数

【问题描述】
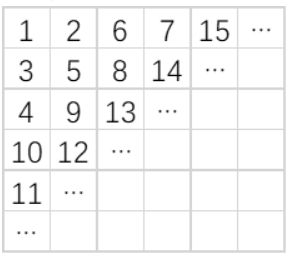
如下图所示，小明用从1 开始的正整数“蛇形”填充无限大的矩阵。

容易看出矩阵第二行第二列中的数是5。请你计算矩阵中第20 行第20 列的数是多少？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

方法一：

//找规律： 1 5 13 25 41 61
#include 
int main()
{
     
	int s=1,k=4;
	for(int i=2;i<=20;i++)
	{
     
		s+=k;
		k+=4;
	}
	printf("%d\n",s);
}

方法二：

//模拟:一次往左下,一次往右上
#include 
int a[100][100];
int cnt=1;
int main()
{
     
	int i;
	int x,y;
    for(i=1;i<=40;i++)
	{
     
        if(i%2==1)//左上
		{
     
            for(x=i,y=1;x>=1&&y<=i;x--,y++)//左上:x--,y++&&x>=1,y<=i&&初始值x=i,y=1;
                a[x][y]=cnt++;
        }
        else//右下
		{
     
            for(int x=1,y=i; x<=i&&y>=1;x++,y--)
                a[x][y]=cnt++;
        }
    }
    printf("%d\n", a[20][20]);
	return 0;
}

试题D 跑步锻炼

【问题描述】
小蓝每天都锻炼身体。
正常情况下，小蓝每天跑 1 千米。如果某天是周一或者月初（1 日），为了
激励自己，小蓝要跑 2 千米。如果同时是周一或月初，小蓝也是跑 2 千米。
小蓝跑步已经坚持了很长时间，从 2000 年 1 月 1 日周六（含）到 2020 年
10 月 1 日周四（含）。请问这段时间小蓝总共跑步多少千米？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

#include
using namespace std;
void xingQi(int &x)//&这个一定要加，不然不能修改x的值
{
     
    if(x == 8)
    {
     
        x = 1;
    }
}
int main()
{
     
    int ans = 0;
    int x = 6;
    int str[15] = {
     0,31,28,31,30,31,30,31,31,30,31,30,31};
    for(int i = 2000; i <= 2020; i++)//年
    {
     
        if((i%4==0 && i%100!=0) || (i%400==0))//判断是否闰年
        {
     
            str[2] = 29;
        }
        else
        {
     
            str[2] = 28;
        }
        for(int j = 1; j <= 12; j++)//月
        {
     
            for(int k = 1; k <= str[j]; k++)//日
            {
     
                ans++;//每天自加1公里
                xingQi(x);//判断是否是周一
                if(x == 1 || k == 1)//如果是周一或月初
                {
     
                    ans++;//再加一公里
                }
                x++;//星期加一
                if(i == 2020 && j == 10 && k == 1)//终止且输出
                {
     
                    cout<< ans << endl;
                }
            }
        }
    }
    return 0;
} 
/*
答案: 8879
*/

E 七段码

【问题描述】
小蓝要用七段码数码管来表示一种特殊的文字。

七段码上图给出了七段码数码管的一个图示，数码管中一共有7 段可以发光的二极管，分别标记为a, b, c, d, e, f, g。小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

方法一：

1:7种
2:10种
3:16种
4:20种
5:19种
6:7种
7:1种
res = 7 + 10 + 16 + 20 + 19 + 7 + 1 = 80

方法二：

#include
using namespace std;
const int N=10;
int use[N],ans,e[N][N],fa[N];
void init()
{
     
	//连边建图，e[i][j]==1表示i和j相邻
	//a b c d e f g
	//1 2 3 4 5 6 7
	e[1][2]=e[1][6]=1;
	e[2][1]=e[2][7]=e[2][3]=1;
	e[3][2]=e[3][4]=e[3][7]=1;
	e[4][3]=e[4][5]=1;
	e[5][4]=e[5][6]=e[5][7]=1;
	e[6][1]=e[6][5]=e[6][7]=1;
}
int find(int u)
{
     
	if(fa[u]==u)return u;    //并查集
	fa[u]=find(fa[u]);
	return fa[u];
}
void dfs(int d)
{
     
	if(d>7)
	{
     
		/* 并查集判联通 */
		for(int i=1; i<=7; i++)fa[i]=i;
		for(int i=1; i<=7; i++)
			for(int j=1; j<=7; j++)
				if(e[i][j]&&use[i]&&use[j])
				{
     
					int fx=find(i),fy=find(j);
					if(fx!=fy)
					{
     
						fa[fx]=fy;
					}
				}
		int k=0;
		for(int i=1; i<=7; i++)if(use[i]&&fa[i]==i)k++;
		if(k==1)ans++;
		return;
	}
	use[d]=1;//打开d这个灯，继续开关下一个灯
	dfs(d+1);
	use[d]=0;//关闭d这个灯，继续开关下一个灯
	dfs(d+1);
}
int main()
{
     
	init();
	dfs(1);
	cout<<ans;
}

程序设计题

F 成绩统计

【问题描述】
小蓝给学生们组织了一场考试，卷面总分为 100 分，每个学生的得分都是
一个 0 到 100 的整数。
如果得分至少是 60 分，则称为及格。如果得分至少为 85 分，则称为优秀。
请计算及格率和优秀率，用百分数表示，百分号前的部分四舍五入保留整
数。

【输入格式】
输入的第一行包含一个整数 n，表示考试人数。
接下来 n 行，每行包含一个 0 至 100 的整数，表示一个学生的得分。

【输出格式】
输出两行，每行一个百分数，分别表示及格率和优秀率。百分号前的部分
四舍五入保留整数。

【样例输入】
7
80
92
56
74
88
100
0
1
2
3
4
5
6
7
8
【样例输出】
71%
43%
1
2
【评测用例规模与约定】
对于50% 的评测用例， 1 ≤ n ≤ 100。
对于所有评测用例，1 ≤ n ≤10000。

#include
int main()
{
     
	double a1=0,a2=0;
	int n,i;
	scanf("%d",&n);
	for(i=0; i<n; i++)
	{
     
		int s;
		scanf("%d",&s);
		if(s>=60) a1++;
		if(s>=85) a2++;
	}
	a1=(a1/n+0.005)*100;
	a2=(a2/n+0.005)*100;
	printf("%d%%\n%d%%",(int)a1,(int)a2);
	return 0;
}

试题 G: 回文日期

时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
2020 年春节期间，有一个特殊的日期引起了大家的注意：2020 年 2 月 2日。因为如果将这个日期按 “yyyymmdd” 的格式写成一个 8 位数是 20200202，恰好是一个回文数。我们称这样的日期是回文日期。
有人表示 20200202 是 “千年一遇” 的特殊日子。对此小明很不认同，因为不到 2 年之后就是下一个回文日期：20211202 即 2021 年 12 月 2 日。
也有人表示 20200202 并不仅仅是一个回文日期，还是一个 ABABBABA型的回文日期。对此小明也不认同，因为大约 100 年后就能遇到下一个ABABBABA 型的回文日期：21211212 即 2121 年 12 月 12 日。算不上 “千年一遇”，顶多算 “千年两遇”。
给定一个 8 位数的日期，请你计算该日期之后下一个回文日期和下一个ABABBABA 型的回文日期各是哪一天。

【输入格式】
输入包含一个八位整数 N，表示日期。

【输出格式】
输出两行，每行 1 个八位数。第一行表示下一个回文日期，第二行表示下一个 ABABBABA 型的回文日期。

【样例输入】
20200202

【样例输出】
20211202
21211212

【评测用例规模与约定】
对于所有评测用例，10000101 ≤ N ≤ 89991231，保证 N 是一个合法日期的 8 位数表示。

#include 
using namespace std;
int months[13] = {
     0,31,28,31,30,31,30,31,31,30,31,30,31};
//判断日期是否合法
bool check(int date)
{
     
	int year = date/10000;
	int month = date/100%100;
	int day = date%100;
	if(!month || month>13 || !day)	return false;
	if(month != 2 && day > months[month])	return false;
	if(month == 2)
	{
     
		bool leap = year%4==0 && year%100 || year%400==0;
		if(day > 28+leap)	return false;
	}
	return true;
}
//判断日期是否为回文日期
bool Ishuiwen(int date)
{
     
	int temp = 0;
	while(date > temp)
	{
     
		temp = temp * 10 + date%10;
		date /= 10;
	}
	if(date == temp)	return true;
	return false;
}

//判断日期是否为ABABBABA型日期
bool IsABhuiwen(int date)
{
     
	int d,m;
	d = date%100;
	m = date/100%100;
	if(Ishuiwen(date) && d==m)	return true;
	return false;
}

int main()
{
     
	int N;
	cin >> N;
	for(int i=N+1; ; i++)
	{
     
		if(check(i) && Ishuiwen(i))
		{
     
			cout << i << endl;
			break;
		}
	}
	for(int i=N+1;; i++)
	{
     
		if(check(i) && IsABhuiwen(i))
		{
     
			cout << i << endl;
			break;
		}
	}
	return 0;
}

试题 H: 子串分值和

时间限制: 1.0s 内存限制: 256.0MB 本题总分：20 分

【问题描述】
对于一个字符串 S，我们定义 S 的分值 f(S ) 为 S 中出现的不同的字符个数。例如 f(”aba”) = 2，f(”abc”) = 3, f(”aaa”) = 1。现在给定一个字符串 S [0…n − 1]（长度为 n），请你计算对于所有 S 的非空子串 S [i… j](0 ≤ i ≤ j < n)，f(S [i… j]) 的和是多少。

【输入格式】
输入一行包含一个由小写字母组成的字符串 S。

【输出格式】
输出一个整数表示答案。

【样例输入】
ababc

【样例输出】
28

【样例说明】

子串 	f值
a 		 1
ab 		 2
aba 	 2
abab 	 2
ababc 	 3
 b 		 1
 ba 	 2
 bab 	 2
 babc 	 3
  a 	 1
  ab 	 2
  abc 	 3
   b 	 1
   bc 	 2
    c 	 1

【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ n ≤ 10；
对于 40% 的评测用例，1 ≤ n ≤ 100；
对于 50% 的评测用例，1 ≤ n ≤ 1000；
对于 60% 的评测用例，1 ≤ n ≤ 10000；
对于所有评测用例，1 ≤ n ≤ 100000。

计算每一个字母的贡献
对于整个的贡献值为与上一个相同字母的距离✖与末端的距离
时间复杂度O(n)

#include
#include
using namespace std;
long long last[26];
int main()
{
     
	string str;
	cin>>str;
	memset(last,-1,sizeof(last));
	int n=str.size();
	long long ans=0;
	int i;
	for(i=0;i<n;i++)
	{
     
		ans+=(i-last[str[i]-'a'])*(n-i);
		last[str[i]-'a']=i;
	}
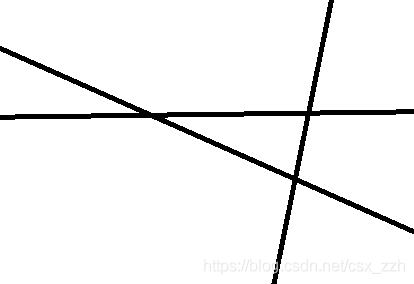
	cout<<ans<<endl;
}

试题I 平面切分

【问题描述】
平面上有 N 条直线，其中第 i 条直线是 y = Ai · x + Bi。
请计算这些直线将平面分成了几个部分。

【输入格式】
第一行包含一个整数 N。
以下 N 行，每行包含两个整数 Ai; Bi。

【输出格式】
一个整数代表答案。

【样例输入】

3
1 1
2 2
3 3

【样例输出】

6

【评测用例规模与约定】
对于 50% 的评测用例， 1 ≤ N ≤ 4, −10 ≤ Ai; Bi ≤ 10。
对于所有评测用例， 1 ≤ N ≤ 1000, −100000 ≤ Ai; Bi ≤ 100000。

题解

第一条直线把直线分成2部分；
第二条直线与现有直线可以有
1）0个交点 三平面 2+(0)+1(平行时) 重和时为2

2）1个交点 四平面 2+(1)+1 (相交时)

两条线时：
重合时平面没有增加------>重合时没有必要再计算
平行时平面+1
相交时平面+2

第三条直线与现有直线可以有
1）0个交点 四平面 3+(0)+1

2）2个交点 六平面=3+(2)+1

3）两个交点 七平面 =4+((2)+1)

三条线时:
当前两条线重合时------->判断两条线
当前两条线平行时
若第三条线与前两条线平行时 平面+1
若第三条线与前两条线相交时 平面+3
当前两条线相交时
若第三条线与前两条线有一个交点时 平面+2
若第三条线与前两条线有两个交点时 平面+3

两条直线求交点函数求出交点坐标
第n条直线与 已有区域 有 num 个交点，则多分（新增）出 num+1 个部分
则所求总区域数更新 ans += num + 1;

首先通过set容器对输入的数据进行去重，根据“每增加一条直线，对平面数增加的贡献值，是其与先前直线的交点数（不包括与已有交点重合的点）+1 ”的结论进行累加，最后输出结果即可

#include
using namespace std;

long double s[1010][2];//存储直线的A，B
long long ans;
bool st[1010]; //false表示不是重边
pair<double,double> p;

int main()
{
     
    int n;
    cin>>n;
    for(int i=0; i<n; i++)
    {
     
        cin>>s[i][0]>>s[i][1];
        set<pair<double,double> > points;
        for(int j=0; j<i; j++)
        {
     
            if(st[j])continue;//直线是重边，跳过
            if(s[i][0]==s[j][0]) //两条直线斜率相等时，判断是平行还是重合
            {
     
                if(s[i][1]==s[j][1])
                {
     
                    st[i]=true;//待添加直线是重边，退出循环
                    break;
                }
                else continue; //直线平行，不需要计算交点
            }
            p.first=(s[j][1]-s[i][1])/(s[i][0]-s[j][0]);//交点的x坐标
            p.second=s[i][0]*p.first+s[i][1];//交点的y坐标
            points.insert(p);
        }
        if(!st[i])ans+=points.size()+1;//若当前直线不是重边，更新答案
    }
    cout<<ans+1;
    return 0;
}

#include
using namespace std;
const int N = 1005;

int main()
{
     
	int n;
	scanf("%d", &n);
	int a, b;
	long double A[N], B[N];
	pair<long double, long double> p; 
	set<pair<long double, long double> > s;  //利用set自动去重功能筛选掉重边 
	for(int i = 0; i < n; i++)
	{
     
		scanf("%d %d", &a, &b);
		p.first = a;
		p.second = b;
		s.insert(p);
	}
	int i = 0;  //将去重后的直线数据放回A,B数组 
	for(set<pair<long double, long double> >::iterator it = s.begin(); it != s.end(); it++, i++)
	{
     
		A[i] = it -> first;
		B[i] = it -> second;
	}
	long long ans = 2;  //初始情况当只有一条直线时，有两个平面 
	for(int i = 1; i < s.size(); i++)  //从下标1开始，也就是第二条直线 
	{
     
		set<pair<long double, long double> > pos;  //记录第i条直线与先前的交点 
		for(int j = i-1; j >= 0; j--)
		{
     
			int a1 = A[i], b1 = B[i];
			int a2 = A[j], b2 = B[j];
			if(a1 == a2)  //遇到平行线无交点，跳出 
				continue; 
			p.first = 1.0*(b2-b1)/(a1-a2);
			p.second = 1.0*a1*((b2-b1)/(a1-a2)) + b1;
			pos.insert(p); 
		}
		ans += pos.size() + 1;  //根据结论，每增加一条直线，对平面数的贡献值是其与先前直线的交点数（不重合）+1 
	} 
	printf("%d\n", ans);
	return 0;
}

试题J 字串排序

【问题描述】
小蓝最近学习了一些排序算法，其中冒泡排序让他印象深刻。
在冒泡排序中，每次只能交换相邻的两个元素。小蓝发现，如果对一个字符串中的字符排序，只允许交换相邻的两个字符，则在所有可能的排序方案中，冒泡排序的总交换次数是最少的。
例如，对于字符串 lan 排序，只需要 1 次交换。对于字符串 qiao 排序，总共需要 4 次交换。
小蓝找到了很多字符串试图排序，他恰巧碰到一个字符串，需要 V 次交换，可是他忘了把这个字符串记下来，现在找不到了。
请帮助小蓝找一个只包含小写英文字母且没有字母重复出现的字符串，对该串的字符排序，正好需要 V 次交换。如果可能找到多个，请告诉小蓝最短的那个。如果最短的仍然有多个，请告诉小蓝字典序最小的那个。请注意字符串中可以包含相同的字符。

【输入格式】
输入的第一行包含一个整数V，小蓝的幸运数字。

【输出格式】
题面要求的一行字符串。

【样例输入】

4

【样例输出】

bbaa

【样例输入】

100

【样例输出】

jihgfeeddccbbaa

【评测用例规模与约定】
对于 30% 的评测用例， 1 ≤ V ≤ 20。
对于 50% 的评测用例， 1 ≤ V ≤ 100。
对于所有评测用例， 1 ≤ V ≤ 10000。

过了50%的样例

#include 
using namespace std;
const int N = 1e4 + 10;
char ans[N], res[N];
int n, len;
bool judge() 
{
     
	int i = len;
	while(ans[i] == res[i] && i) i--;
	return res[i] < ans[i];
}
void dfs(int now, int maxn, int m, int sum) {
     
	if(sum == n) 
	{
     
		if(m < len || (m == len && judge()))
		{
     
			len = m;
			for(int i = 1; i <= len; i++) 	ans[i] = res[i];
		}
		return;
	}
	if(now >= 26) return ;
	for(int i = 1; i <= maxn; i++) 
	{
     
		int temp = sum + m * i;
		if(temp > n) return ;
		res[m + i] = char(now + 'a');
		dfs(now + 1, i, m + i, temp);
	}
}

int main()
{
     
    len = 0x3f3f3f3f;
    scanf("%d", &n);
    dfs(0, 8, 0, 0);
    for(int i = len; i >= 1; i--)
		putchar(ans[i]);
	return 0;
}