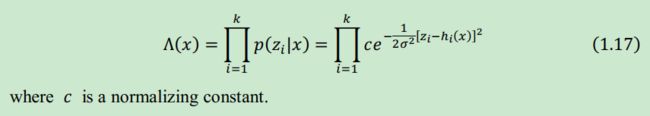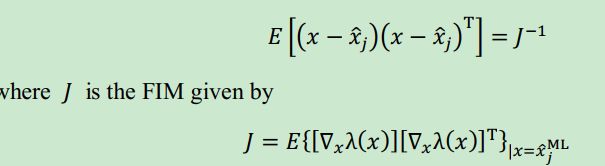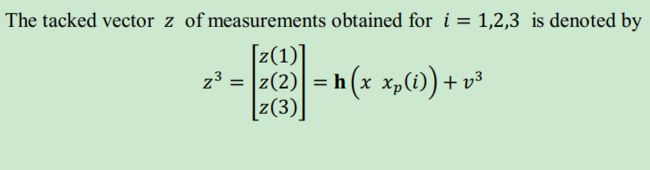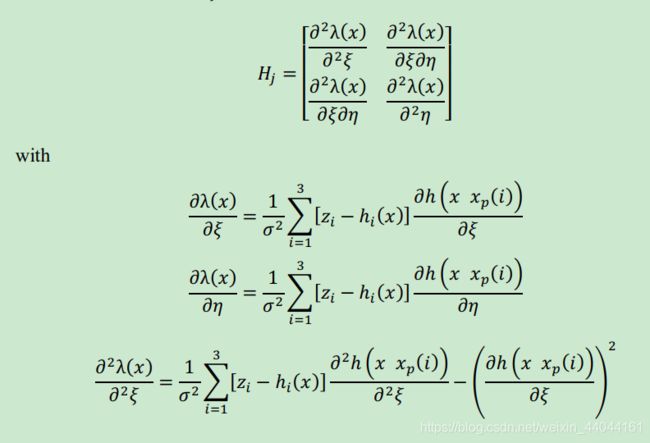角度测量(AOA/DOA)室内定位-迭代最小二乘和高斯牛顿法\MATLAB
角度测量(AOA/DOA)室内定位-迭代最小二乘和高斯牛顿法\MATLAB
原创不易,路过的各位大佬请点个赞
二维仅角度测量的定位问题;
方法:1-非线性最小二乘估计-迭代最小二乘求解
2-极大似然估计-高斯牛顿法求解
性能指标:RMSE(蒙特卡洛),CRLB**
目录
- 角度测量(AOA/DOA)室内定位-迭代最小二乘和高斯牛顿法\MATLAB
- 1. 算法原理
-
- 1.1 广义量测函数
- 1.2 迭代最小二乘
- 1.3 最大似然估计—高斯牛顿法
- 2. 量测方程(AOA定位)
-
- 2.1 雅可比矩阵
- 2.2 海森矩阵
- 3. 参考代码
1. 算法原理
1.1 广义量测函数
![]()
1.2 迭代最小二乘
![]()
CRLB:
![]()
1.3 最大似然估计—高斯牛顿法
2. 量测方程(AOA定位)
2.1 雅可比矩阵
2.2 海森矩阵
3. 参考代码
clc;
close all;
clear all;
N=50;%迭代次数
deta=0;
Runs=350;%Monte karlo
ml_runx=0;
ml_runy=0;
ls_runx=0;
ls_runy=0;
%%initial varient
ls_res=zeros(2,N);
ls_v=zeros(2,N);
ls_x=zeros(1,N);
ls_y=zeros(1,N);
%%ML变量定义
ml_res=zeros(2,N);
ml_v=zeros(2,N);
ml_x=zeros(1,N);
ml_y=zeros(1,N);
d0=0.5;%迭代终止条件
% T=1;%采样周期
%target
xp=20000;
yp=20000;%目标位置
vp=[xp;yp];
x=zeros(1,50);
y=zeros(1,50);
%sensor
x1=0;y1=0;
x2=15000;y2=5000;
x3=30000;y3=0;%传感器位置,三个
v1=[x1;y1];
v2=[x2;y2];
v3=[x3;y3];
y=[y1,y2,y3];
x=[x1,x2,x3];
Z=zeros(3,1);%传感器量测数据
z1=0;z2=0;z3=0;
Z(1,1)=z1;
Z(2,1)=z2;
Z(3,1)=z3;
%非线性函数
h01=0;h02=0;h03=0;
H0=zeros(3,1);
H=zeros(3,1);
%噪声
w=zeros(3,1);
Q=(pi/180)^2;%noise variance
% hatv=zeros(2,1);%v=[x;y]
%%
% nonlinear funchtion h() matraix
h01=atan2(yp-y1,xp-x1);
h02=atan2(yp-y2,xp-x2);
h03=atan2(yp-y3,xp-x3);%真实位置信息
H0(1,1)=h01;
H0(2,1)=h02;
H0(3,1)=h03;
for i=1:1:Runs;
%white gassian noise
w=sqrt(Q)*randn(3,1);
%measuremen z
Z=H0+w;
z1=Z(1,1);
z2=Z(2,1);
z3=Z(3,1);
%LS估计初值
ls_x0=(x3*tan(z3)-x1*tan(z1)-y3+y1)/(tan(z3)-tan(z1)); %20060;%初始位置
ls_y0=((x1-x3)*tan(z1)*tan(z3)-y1*tan(z3)+y3*tan(z1))/(tan(z1)-tan(z3)); %19770;y纵坐标初始位置
ls_v0=[ls_x0;ls_y0];
%ML估计初值
ml_x0=ls_x0;
ml_y0=ls_y0;
ml_v0=[ml_x0;ml_y0];
%ML迭代
for t=1:1:N;
if(t==1)
ml_res(:,t)=ml_v0;
ml_v(:,1)=ml_v0;
ml_x(t)=ml_x0;
ml_y(t)=ml_y0;
else
%H矩阵:ml_h
ml_h(1,1)=atan2(ml_y(t-1)-y1,ml_x(t-1)-x1);
ml_h(2,1)=atan2(ml_y(t-1)-y2,ml_x(t-1)-x2);
ml_h(3,1)=atan2(ml_y(t-1)-y3,ml_x(t-1)-x3);
%雅可比矩阵ml_J
ml_J(1,1)=-(ml_y(t-1)-y1)/((ml_x(t-1)-x1)^2+(ml_y(t-1)-y1)^2);
ml_J(1,2)=(ml_x(t-1)-x1)/((ml_x(t-1)-x1)^2+(ml_y(t-1)-y1)^2);
ml_J(2,1)=-(ml_y(t-1)-y2)/((ml_x(t-1)-x2)^2+(ml_y(t-1)-y2)^2);
ml_J(2,2)=(ml_x(t-1)-x2)/((ml_x(t-1)-x2)^2+(ml_y(t-1)-y2)^2);
ml_J(3,1)=-(ml_y(t-1)-y3)/((ml_x(t-1)-x3)^2+(ml_y(t-1)-y3)^2);
ml_J(3,2)=(ml_x(t-1)-x3)/((ml_x(t-1)-x3)^2+(ml_y(t-1)-y3)^2);
%函数h的二阶梯度ml_JJ
for i=1:3
ml_JJ(i,1)=(2*(ml_y(t-1)-y(i))*(ml_x(t-1)-x(i)))/((ml_y(t-1)-y(i))^2+(ml_x(t-1)-x(i))^2)^2;
ml_JJ(i,2)=-(2*(ml_y(t-1)-y(i))*(ml_x(t-1)-x(i)))/((ml_y(t-1)-y(i))^2+(ml_x(t-1)-x(i))^2)^2;
ml_JJ(i,3)=((ml_y(t-1)-y(i))^2-(ml_x(t-1)-x(i))^2)/((ml_y(t-1)-y(i))^2+(ml_x(t-1)-x(i))^2)^2;
end
%一阶梯度矩阵ml_F
ml_F(1,1)=1/Q*((z1-ml_h(1,1))*ml_J(1,1)+(z2-ml_h(2,1))*ml_J(2,1)+(z3-ml_h(3,1))*ml_J(3,1));
ml_F(2,1)=1/Q*((z1-ml_h(1,1))*ml_J(1,2)+(z2-ml_h(2,1))*ml_J(2,2)+(z3-ml_h(3,1))*ml_J(3,2));
%Hessian矩阵:ml_H
ml_H(1,1)=((z1-ml_h(1,1))*ml_JJ(1,1)-(ml_J(1,1))^2+(z2-ml_h(2,1))*ml_JJ(2,1)-(ml_J(2,1))^2+(z3-ml_h(3,1))*ml_JJ(3,1)-(ml_J(3,1))^2)/Q;
ml_H(2,2)=((z1-ml_h(1,1))*ml_JJ(1,2)-(ml_J(1,2))^2+(z2-ml_h(2,1))*ml_JJ(2,2)-(ml_J(2,2))^2+(z3-ml_h(3,1))*ml_JJ(3,2)-(ml_J(3,2))^2)/Q;
ml_H(1,2)=((z1-ml_h(1,1))*ml_JJ(1,3)-(ml_J(1,1))*(ml_J(1,2))+(z2-ml_h(2,1))*ml_JJ(2,3)-(ml_J(2,1))*(ml_J(2,2))+(z3-ml_h(3,1))*ml_JJ(3,3)-(ml_J(3,1))*(ml_J(3,2)))/Q;
ml_H(2,1)=ml_H(1,2);
%ML迭代
ml_v(:,t)=ml_v(:,t-1)-inv(ml_H)*ml_F;
end
ml_res(:,t)=ml_v(:,t);
ml_x(t)=ml_v(1,t);
ml_y(t)=ml_v(2,t);
end
for k=1:50;
ml_runx=ml_runx+(xp-ml_x(k))^2;
ml_runy=ml_runy+(yp-ml_y(k))^2;
end
%%LS迭代
for t=1:1:N;%迭代不超过50次
if(t==1)
ls_res(:,t)=ls_v0;
ls_v(:,1)=ls_v0;
ls_x(t)=ls_x0;
ls_y(t)=ls_y0;
else
%H矩阵
ls_h1=atan2(ls_y(t-1)-y1,ls_x(t-1)-x1);
ls_h2=atan2(ls_y(t-1)-y2,ls_x(t-1)-x2);
ls_h3=atan2(ls_y(t-1)-y3,ls_x(t-1)-x3);
ls_H(1,1)=ls_h1;
ls_H(2,1)=ls_h2;
ls_H(3,1)=ls_h3;
%J矩阵
ls_J(1,1)=-(ls_y(t-1)-y1)/((ls_x(t-1)-x1)^2+(ls_y(t-1)-y1)^2);
ls_J(1,2)=(ls_x(t-1)-x1)/((ls_x(t-1)-x1)^2+(ls_y(t-1)-y1)^2);
ls_J(2,1)=-(ls_y(t-1)-y2)/((ls_x(t-1)-x2)^2+(ls_y(t-1)-y2)^2);
ls_J(2,2)=(ls_x(t-1)-x2)/((ls_x(t-1)-x2)^2+(ls_y(t-1)-y2)^2);
ls_J(3,1)=-(ls_y(t-1)-y3)/((ls_x(t-1)-x3)^2+(ls_y(t-1)-y3)^2);
ls_J(3,2)=(ls_x(t-1)-x3)/((ls_x(t-1)-x3)^2+(ls_y(t-1)-y3)^2);
%噪声R
R=eye(3)*Q;
ls_v(:,t)=ls_v(:,t-1)+inv(ls_J'*inv(R)*ls_J)*ls_J'*inv(R)*(Z-ls_H);%最小二乘迭代位置状态拟合
end
% deta=hatx(t)-hatx(t-1);%判断迭代终止;
% if deta<=d0
% break;
% end
ls_res(:,t)=ls_v(:,t);
ls_x(t)=ls_v(1,t);
ls_y(t)=ls_v(2,t);
end
for k=1:50;
ls_runx=ls_runx+(xp-ls_x(k))^2;
ls_runy=ls_runy+(yp-ls_y(k))^2;
end
end
%Monte karlo runs
ml_Runs_x=sqrt(ml_runx/(Runs*N))
ml_Runs_y=sqrt(ml_runy/(Runs*N))
ls_Runs_x=sqrt(ls_runx/(Runs*N))
ls_Runs_y=sqrt(ls_runy/(Runs*N))
%fisher 信息
%J矩阵,代入真值
J(1,1)=-(yp-y1)/((xp-x1)^2+(yp-y1)^2);
J(1,2)=(xp-x1)/((xp-x1)^2+(yp-y1)^2);
J(2,1)=-(yp-y2)/((xp-x2)^2+(yp-y2)^2);
J(2,2)=(xp-x2)/((xp-x2)^2+(yp-y2)^2);
J(3,1)=-(yp-y3)/((xp-x3)^2+(yp-y3)^2);
J(3,2)=(xp-x3)/((xp-x3)^2+(yp-y3)^2);
% FI(1,1)=((z1-h01)*JI(1,1)+(z2-h02)*JI(2,1)+(z3-h03)*JI(3,1))/Q;
% FI(2,1)=((z1-h01)*JI(1,2)+(z2-h02)*JI(2,2)+(z3-h03)*JI(3,2))/Q;
FIM(1,1)=((J(1,1))^2+(J(2,1))^2+(J(3,1))^2)/Q;
FIM(2,2)=((J(1,2))^2+(J(2,2))^2+(J(3,2))^2)/Q;
FIM(1,2)=(J(1,1)*J(1,2)+J(2,1)*J(2,2)+J(3,1)*J(3,2))/Q;
FIM(2,1)=(J(1,1)*J(1,2)+J(2,1)*J(2,2)+J(3,1)*J(3,2))/Q;
ml_MSE=inv(FIM);
ml_CRLB_x=sqrt(ml_MSE(1,1))
ml_CRLB_y=sqrt(ml_MSE(2,2))
%LS:MSE
ls_MSE=inv(J'*inv(R)*J);
ls_CRLB_x=sqrt(ls_MSE(1,1))
ls_CRLB_y=sqrt(ls_MSE(2,2))
%结果比较
t=1:1:10;
figure(1);
plot(t,ls_res(1,t),t,ml_res(1,t),'r--')
title('Estimation of East Position')
xlabel('Iteration j'), ylabel('The East Position');
legend('ILS','ML')
hold on;
figure(2);
plot(t,ls_res(2,t),t,ml_res(2,t),'r--')
title('Estimation of North Position')
xlabel('Iteration j'), ylabel('The North Position');
legend('ILS','ML');
figure(3);
plot([x1 xp],[y1 xp],'-o');hold on;
plot([x2 xp],[y2 yp],'-o');hold on;
plot([x3 xp],[y3 yp],'-o');hold on;
plot(xp,yp,'*');
axis([-10000 50000 -10000 50000]);
xlabel('East(m)'), ylabel('North(m)');