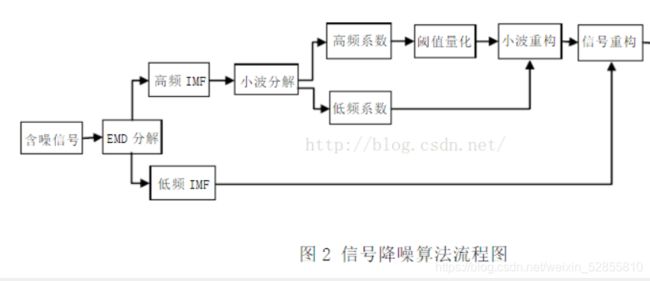
小波变换初学者笔记

小波变换–数据处理

在进行深度学习训练时会使用到大量的数据，这些数据中有会存在一些噪声，小波变换可以用来去除数据中的噪声。

一、什么是小波变换

关于小波变换的理解可以参考的资料有很多，这里放一个比较通俗易懂的链接。小波变换通俗理解
简单来说可以理解成和高数中的傅里叶变化类似的工具，把一个信号分解成多个，但是与傅里叶变换又有不同。
小波变换数学表达式

基本小波的函数作位移t后，再在不同尺度a下与待分析信号f(t)作内积。尺度函数从滤波器的角度来看是低通滤波器，而小波函数是高通滤波器。

（公式不好打，我直接上图了）

二、连续小波变换（CWT)和离散小波变换（DWT）

连续小波变换（CWT）
离散小波变换（DWT）

连续小波变换a,b都连续，离散小波变换a,b都不连续。因为离散小波变换的a经常是2的幂所以也叫二进制小波。

三、小波变换步骤

1、选取合适的wavelet function 和 scaling function，从已有的信号中反算出系数c, d
2、对系数做对应处理
3、从处理后的系数中重新构建信号

四、 CWT连续小波变换实例（python）

首先放从大佬那看到的代码，ecg心电信号去噪的例子。原博客链接

import matplotlib.pyplot as plt
import pywt

# Get data:
ecg = pywt.data.ecg()  # 生成心电信号
index = []
data = []
for i in range(len(ecg)-1):
    X = float(i)
    Y = float(ecg[i])
    index.append(X)
    data.append(Y)

# Create wavelet object and define parameters
w = pywt.Wavelet('db8')  # 选用Daubechies8小波
t = w.dec_len
maxlev = pywt.dwt_max_level(len(data), w.dec_len) #计算最大有用分解级别。 dwt_max_level(data_len, filter_len) filter_len : int, str or Wavelet小波滤波器的长度。 或者，可以指定离散小波或小波对象的名称。
print("maximum level is " + str(maxlev))
threshold = 0.04  # Threshold for filtering 过滤域值

# Decompose into wavelet components, to the level selected:分解为小波分量，达到所选水平
coeffs = pywt.wavedec(data, 'db8', level=maxlev)  # 将信号进行小波分解

plt.figure()
for i in range(1, len(coeffs)):
    coeffs[i] = pywt.threshold(coeffs[i], threshold*max(coeffs[i]))  # 将噪声滤波

datarec = pywt.waverec(coeffs, 'db8')  # 将信号进行小波重构
print(type(datarec))

mintime = 0
maxtime = mintime + len(data) + 1

plt.figure()
plt.subplot(2, 1, 1)
plt.plot(index[mintime:maxtime], data[mintime:maxtime])
plt.xlabel('time (s)')
plt.ylabel('microvolts (uV)')
plt.title("Raw signal")
plt.subplot(2, 1, 2)
plt.plot(index[mintime:maxtime], datarec[mintime:maxtime-1])
plt.xlabel('time (s)')
plt.ylabel('microvolts (uV)')
plt.title("De-noised signal using wavelet techniques")

plt.tight_layout()
plt.show()

运行结果图：

根据这个例子，对深度学习使用的数据进行处理。

from matplotlib import pyplot as plt
import pandas as pd
import pywt
import matplotlib

#我们在使用matplotliblib画图的时候经常会遇见中文或者是负号无法显示的情况，pylot使用rc配置文件来自定义图形的各种默认属性，称之为rc配置或rc参数
#matplotlib.rcParams['font.size']=40  #font.size’ 字体大小，整数字号或者’large’   ‘x-small’
matplotlib.rcParams['font.family']='Microsoft Yahei'  #‘font.family’ 用于显示字体的名字 font.style’ 字体风格，正常’normal’ 或斜体’italic’
matplotlib.rcParams['font.weight'] = 'bold'

SaveFile_Path = r'D:\Desktop\2018年5MW运行数据\2018年\处理后数据'  # 要读取和保存的文件路径
threshold = 0.04 # Threshold for filtering 过滤域值

def wavetransform(col):
    df = pd.read_csv(SaveFile_Path + '\\' + 'pre.csv', header=0, index_col=0, encoding='gbk')
    values = df.values

    # Create wavelet object and define parameters
    w = pywt.Wavelet('db8')  # 选用Daubechies8小波
    t = w.dec_len
    maxlev = pywt.dwt_max_level(df.shape[0], w.dec_len) #计算最大有用分解级别。 dwt_max_level(data_len, filter_len) filter_len : int, str or Wavelet小波滤波器的长度。 或者，可以指定离散小波或小波对象的名称。
    print("maximum level is " + str(maxlev))

    # Decompose into wavelet components, to the level selected:分解为小波分量，达到所选水平
    coeffs = pywt.wavedec(values[:, col], 'db8', level=maxlev)  # 将信号进行小波分解
    for j in range(1, len(coeffs)):
        coeffs[j] = pywt.threshold(coeffs[j], threshold * max(coeffs[j]))  # 将噪声滤波
    datarec = pywt.waverec(coeffs, 'db8')  # 将信号进行小波重构
    return values, datarec

def main():
    df = pd.read_csv(SaveFile_Path + '\\' + 'pre.csv', header=0, index_col=0, encoding='gbk')
    col = df.shape[1]
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    f1 = plt.figure()

    for i in range(0, col):
        values, datarec = wavetransform(i)
        plt.subplot(col, 2, 2*i + 1)
        plt.plot(values[:, i])
        plt.title(df.columns[i], y=0.5, loc='right')
        plt.subplot(col, 2, 2*i + 2)
        plt.plot(datarec)
        plt.title(df.columns[i] + '__小波变换', y=0.5, loc='right')

    plt.show()



if __name__ == '__main__':
    main()

运行结果：

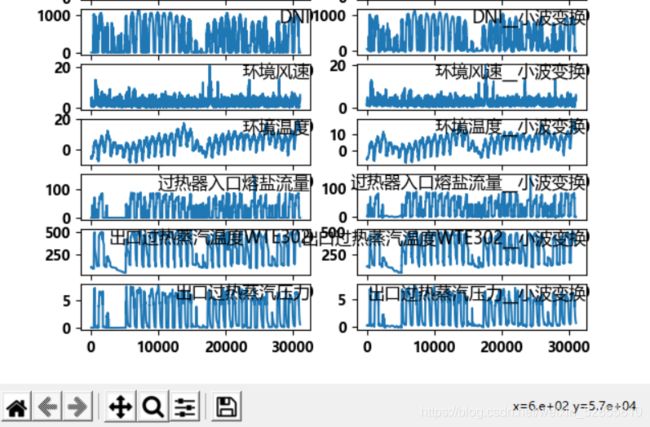
我这里对深度学习所使用的每个特征量都使用了小波变换去噪，代码中，threshold是阈值，使用pywt.threshold需要一个阈值，至于筛选的方式则按你所选择的模式，规则如下官方文档。阈值的选取非常重要，但是目前没有较好的确定阈值设为多大合理，只能自己慢慢试验。
其中pywt.dwt_max_level(data_len, filter_len)是求最大分解级别，data_len数据长度， filter_len分解滤波器长度。具体可以去官方文档看看。

五、离散小波变换（DWT）实例

仍旧先看大佬的，原博客链接
这里我以我的第一个特征量的数据为例，对单一个特征量进行一阶分解，这段代码并没有将分解后低频分量和高频分量进行重构，但是低频分量和原始数据的趋势大致相似。

from matplotlib import pyplot as plt
import pandas as pd
import pywt
import matplotlib

matplotlib.rcParams['font.family']='Microsoft Yahei'  #‘font.family’ 用于显示字体的名字 font.style’ 字体风格，正常’normal’ 或斜体’italic’
matplotlib.rcParams['font.weight'] = 'bold'

SaveFile_Path = r'D:\Desktop\2018年5MW运行数据\2018年\处理后数据'  # 要读取和保存的文件路径
threshold = 0.04 # Threshold for filtering 过滤域值
WAVES = 5


def plot_signal_decomp(data, w):
    mode = pywt.Modes.smooth
    """Decompose and plot a signal S.
    S = An + Dn + Dn-1 + ... + D1 #信号重构
    """
    w = pywt.Wavelet(w)#选取小波函数
    a = data
    ca = []#近似分量
    cd = []#细节分量
    for i in range(5):
        (a, d) = pywt.dwt(a, w, mode)#进行1阶离散小波变换
        ca.append(a)
        cd.append(d)

    rec_a = []
    rec_d = []
    for i, coeff in enumerate(ca):
        coeff_list = [coeff, None] + [None] * i #填充长度
        rec_a.append(pywt.waverec(coeff_list, w))#小波重构

    for i, coeff in enumerate(cd):
        coeff_list = [None, coeff] + [None] * i
        rec_d.append(pywt.waverec(coeff_list, w))

    print(len(rec_a))
    print(len(rec_d))
    fig = plt.figure()
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.subplot(3, 1, 1)
    plt.plot(data, label='原始数据曲线')
    plt.legend()

    plt.subplot(3, 1,2)
    plt.plot(rec_a[-1],'r', label='低频曲线趋势')
    plt.legend()

    plt.subplot(3, 1, 3)
    plt.plot(rec_d[0],'g', label='高频曲线噪声')
    plt.legend()
    plt.show()
datas = pd.read_csv(SaveFile_Path + '\\' + 'pre.csv', header=0, index_col=0, encoding='gbk')
values = datas.values
plot_signal_decomp(values[:, 0], 'db4')#这里选择sym5小波，小波还有

运行结果：

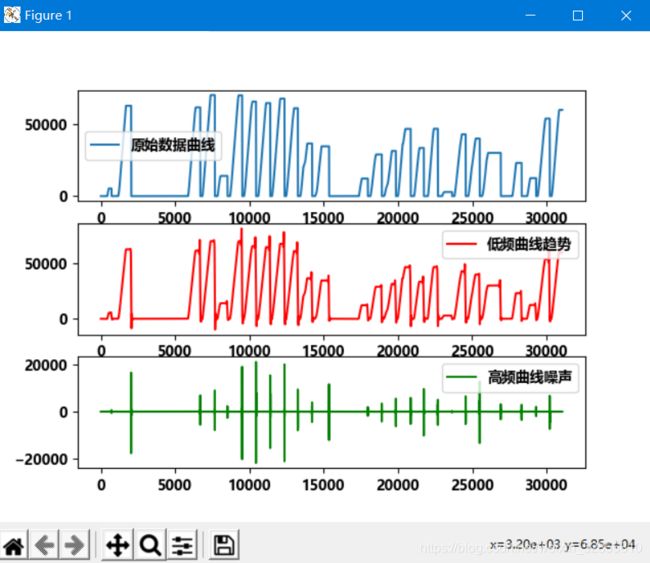
当进行多层分解时，每一层分解的结果都是上次分解的低频信号再分解成低频和高频两部分，D代表高频，A代表低频，第一层X=D1+A1，第二层，A1=D2+A2，第三层A2=D3+A3… X=D1+D2+D3+…+AN。一一段matlab代码为例我们来看看：

% By lyqmath
% DLUT School of Mathematical Sciences 2008
% BLOG：http://blog.sina.com.cn/lyqmath
clc; clear all; close all;
load leleccum; % 载入信号数据
s = leleccum;
Len = length(s);
[ca1, cd1] = dwt(s, 'db1'); % 采用db1小波基分解
a1 = upcoef('a', ca1, 'db1', 1, Len); % 从系数得到近似信号
d1 = upcoef('d', cd1, 'db1', 1, Len); % 从系数得到细节信号
s1 = a1+d1; % 重构信号
figure;
subplot(2, 2, 1); plot(s); title('初始电源信号');
subplot(2, 2, 2); plot(ca1); title('一层小波分解的低频信息');
subplot(2, 2, 3); plot(cd1); title('一层小波分解的高频信息');
subplot(2, 2, 4); plot(s1, 'r-'); title('一层小波分解的重构信号');

运行结果：

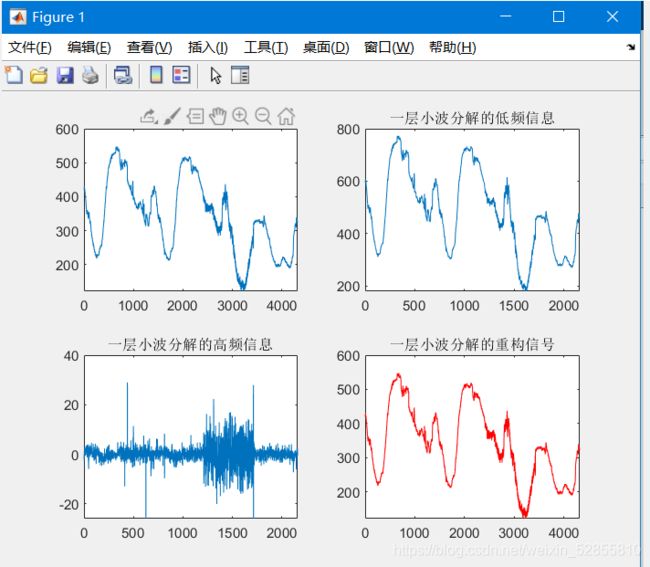
我们以多层分解继续来进行研究，还是以深度学习需要的多个特征量一起来进行研究，多个特征量一起分解，然后根据 X=D1+D2+D3+…+AN进行信号重构，得到去噪后的数据，（这里我也没有明白为什么不能直接用低频数据，要进行重构）。代码中，也没有对高频部分进行阈值量化，只是分解之后进行重构。

from matplotlib import pyplot as plt
import pandas as pd
import pywt
import matplotlib

SaveFile_Path = r'D:\Desktop\2018年5MW运行数据\2018年\处理后数据'  # 要读取和保存的文件路径
threshold = 0.04 # Threshold for filtering 过滤域值
WAVES = 5

data_list = []
a5_list = []
d1_list = []
d2_list = []
d3_list = []
d4_list = []
d5_list = []
d6_list = []

def plot_signal_decomp(data, wavelet, WAVES):
    """Decompose and plot a signal S.
    S = An + Dn + Dn-1 + ... + D1
    """
    w = pywt.Wavelet(wavelet)  # 选取小波函数
    a = data
    ca = []  # 近似分量
    cd = []  # 细节分量

    for i in range(WAVES):  # WAVES小波分解层数
        (a, d) = pywt.dwt(a, w, mode='sym')  # 进行5阶离散小波变换
        ca.append(a)
        cd.append(d)

    rec_a = []
    rec_d = []

    for i, coeff in enumerate(ca):  # enumerate(sequence, [start=0]),将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，一般用在 for 循环当中。
        coeff_list = [coeff, None] + [None] * i  #填充长度
        rec_a.append(pywt.waverec(coeff_list, w))  # 重构

    for i, coeff in enumerate(cd):
        coeff_list = [None, coeff] + [None] * i
        rec_d.append(pywt.waverec(coeff_list, w))

    data_list.append(data)
    a5_list.append(rec_a[-1])
    for i in range(1, WAVES + 1):
        globals()['d{}_list'.format(i)].append(rec_d[i - 1])

    return rec_d[0][:len(rec_d[0])] + rec_d[1][:len(rec_d[0])] + rec_d[2][:len(
        rec_d[0])]  # + rec_d[3][:len(rec_d[0])]+ rec_d[4][:len(rec_d[0])] #+ rec_d[5][:len(rec_d[0])]

def main():
    datas = pd.read_csv(SaveFile_Path + '\\' + 'pre.csv', header=0, index_col=0, encoding='gbk')
    dfNew = pd.DataFrame()
    num = datas.shape[1]
    values = datas.values
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.figure()
    i = 0

    for col in datas.columns[1:]:
        print('正在执行%s小波分解...'% col)
        cd = plot_signal_decomp(datas[col].values, 'db4', WAVES)
        dfNew[col] = cd
        plt.subplot(num, 2, 2 * i + 1)
        plt.plot(values[:, i])
        plt.title(datas.columns[i], y=0.5, loc='right')
        plt.subplot(num, 2, 2 * i + 2)
        plt.plot(cd)
        plt.title(datas.columns[i] + '__小波变换', y=0.5, loc='right')
        i += 1
    plt.show()

if __name__ == '__main__':
    main()

尺度与分解频率成反比，分解层数是对频率范围进行一定的划分。从论文中来看，用离散小波变换的显然更多，目前还没有搞清什么情景下适合使用连续小波变换。

六、总结

以上，就是目前学习小波变换的收获。还有如下疑惑没有解决：
1、小波变换可以只取低频部分不进行重构吗？或是舍去某些高频部分？
2、为什么
for i, coeff in enumerate(ca):
coeff_list = [coeff, None] + [None] * i #填充长度
rec_a.append(pywt.waverec(coeff_list, w))#小波重构
要有coeff_list = [None, coeff] + [None]*i填充长度？
3、什么情景下应该用CWT、什么情景下应该用DWT？
4、小波分解层数的影响？
5、只进行分解和重构不加阈值处理可以降噪吗？

还有以下博客的内容我觉得也很有用：
小波工具箱、小波阈值去噪的说明、Python小波分析库Pywavelets的一点使用心得、选择小波的方法、小波的选择和小波的分类、小波滤波及小波基函数的选择、
以上参考好多优秀的博客，主要是当作自己的笔记来看，如有侵权，马上就删，欢迎大家一起交流学习~

代码全上传github上了https://github.com/sw1122/wavetransform.git