基于极限学习机(ELM)的遗传算法(GA)优化:附Python完整代码【保姆教学超详细】
目录
- 一、前言
-
- 问题的引出
- ELM-GA模型的特点以及优势
- 二、基础知识
-
- ELM模型
- 目标函数/损失函数
- 遗传算法
- 三、代码的实现
-
- 构建神经网络
- 构建遗传算法
- 调控程序
- ELM-GA模型二分类及优化GA模型效果展示
- 四、总结与展望
-
- 本模型的不足之处
- 致谢与参考文献
- 五、附录:完整代码
-
- ELM
- GA
版权声明:如需对此文章代码进行转载请注明出处,若用于商业用途、论文写作请联系作者邮箱[email protected]
一、前言
问题的引出
极限学习机(ELM)算法,随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值,且在训练过程中无需调整,只需设置隐含层神经元的个数,便可获得唯一的最优解,与传统的BP神经网络算法相比,ELM方法学习速度快、泛化性能好。但和传统的神经网络相比一样容易陷入局部最优的问题,继而打算引入遗传算法GA,通过数据交叉、变异和可迭代收敛等特点达到全局最优解的效果。
ELM-GA模型的特点以及优势
- 本模型是基于极限学习机和遗传算法两种的优化和组合,结合了ELM的多层算法深度学习以及GA在进化过程中的多样性和收敛性。在实际训练后,得到了综合80%的预测成果。 本模型的创新和特点如下:
- ELM算法相比传统的BP神经网络,没有负反馈多层迭代的大量数学计算,极大的减少了算法的运算时间同时又满足了隐藏层进行非线性运算的需求。
- GA算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
- 在多层神经网络内的隐藏层和输出层运用了Evolutionary Extreme Learning Machine with novel activation function for credit scoring这一篇论文中对于ELM结合BA算法创建的的全新激活函数
- 在GA中生物选择过程中,优化了原有的“赌盘”选择方式。采用了独创的建立“死亡名单”并随机复制幸存者的方式进行挑选。
- 在GA中基因交叉部分和变异部分,都以对应的基因维度进行运算,达到了不同物种间在相同隐藏层和相同样本特征层进行交叉和变异。实现了GA算法中隐藏层参数矩阵的预测。
- 基于两种机器学习的模型的组合,对于很多样本能够达到迭代几次就产生不错结果的效果,对于数据预测可以节省很多的时间。
- 本版本的遗传算法可以直接计算逼近0的最小值的函数,而非像铺天盖地求最大值的算法,计算可以直接代替在任何求损失函数最小的环节,在机器学习的各类模型中通用型极强。
二、基础知识
ELM模型
极限学习机(ELM)用来训练单隐藏层前馈神经网络(SLFN)与传统的SLFN训练算法不同,极限学习机随机选取输入层权重和隐藏层偏置,输出层权重通过最小化由训练误差项和输出层权重范数的正则项构成的损失函数,依据Moore-Penrose(MP)广义逆矩阵理论计算解析求出。理论研究表明,即使随机生成隐藏层节点,ELM仍保持SLFN的通用逼近能力。在过去的十年里,ELM的理论和应用被广泛研究,从学习效率的角度来看,极限学习机具有训练参数少、学习速度快、泛化能力强的优点。
传统的ELM具有单隐含层,在与其它浅层学习系统,例如单层感知机(single layer perceptron)和支持向量(Support Vector Machine, SVM)相比较时,被认为在学习速率和泛化能力方面可能具有优势 。ELM的一些改进版本通过引入自编码器构筑或堆叠隐含层获得了深度结构,能够进行表征学习。以下我简单介绍一下它的结构:
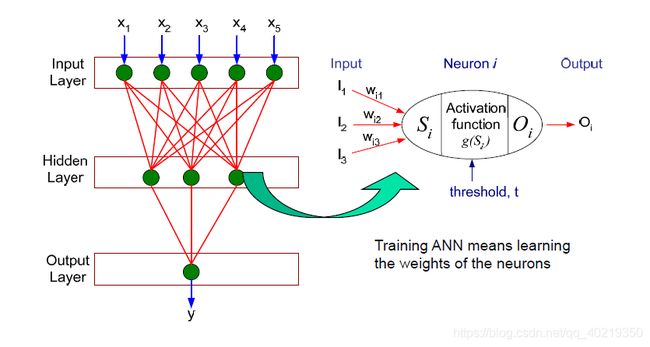
我们可以看到它主要分为输入层I,隐含层H,输出层O。在这个结构图中最重要的不是圆圈,而是其间的连线。下面用通俗的说一下:
输入层的圆圈代表了一个神经元,代表了每一个样本特征,也就是我们所收集到的每个样本的不同参数x1x2x3……。中间的隐含层则是我们俗称的黑箱子,神经网络会通过我们设置的隐含层层数N将这些不同的样本特征映射到一个新的N维空间,这也是隐含层圆圈的数量。最外面的输出层会把最后隐含层得到的相关数据最后打包通过运算让我们得到最终的预测结果。
我们来推导一下神经网络内部的计算过程:
- 首先我们获得M个样本,每个样本具有n个参数,我们设置N个隐藏层就会形成以下结构:
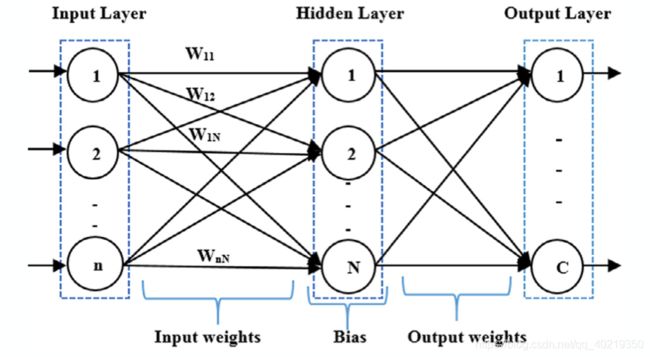
- 我们用W描述每条线段代表的权重,右下角表示连线两端代表所连接的神经元,用beta描述隐藏层的偏执那么就容易得到以下矩阵:
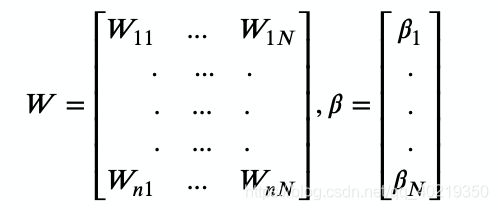
- 我们把每这些权重和偏执带入样本,就可以得到输入层传入隐藏层后的结果,隐藏层在接收到信号后,我们要对N个神经元用激活函数进行激活,激活后,我们就可以从隐藏层传递出去了,以下是描述这个过程的H矩阵:
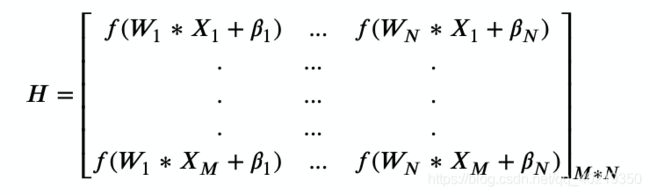
- 我们选用Evolutionary Extreme Learning Machine with novel activation function for credit scoring论文中使用的激活函数,p值反映了激活函数在x附近斜率变化的速度:
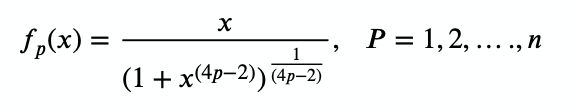
- 我们此时已经得到了隐藏层输出的数据,还需要最后的隐藏层权重,隐藏层权重可以通过最小二乘法得到,由于本文不是重点讨论这个问题,因此直接甩出公式,其中C代表的是约束系数,以免过于拟合:
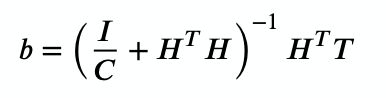
- 有了以上的到的信息,我们不难得到最后的输出值:
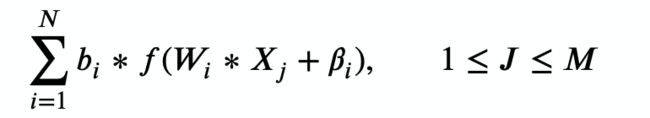
以上就是从输入层到输出层的推导,不过呢这也仅仅是一个样本,实际操作过程中,我们需要处理至少上百上千个样本。当数据集越多的时候,我们通过神经网络预测的也就越准。而对于隐藏层N的设置因处理的样本而异。
目标函数/损失函数
我们的预测模型虽然得出来了,但样本的权重,隐藏层权重从哪来的,而我们又怎么知道它算的准备准好不好呢?那么以下就是介绍的就是重点:
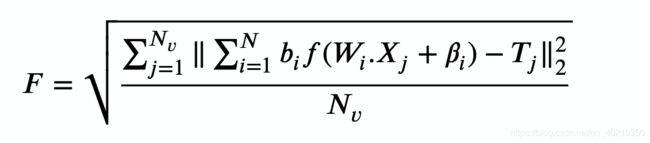
如果学过计量经济学的话应该知道,我们最终得到的残差即表示最终模型拟合的效果,残差越大说明模型效果越差,反之越好。通俗的来讲,我们通过计算得到一个值predict,我们那这个值和最后的真实值做对比我们就会得到一个差值,而这个就是所谓的残差。在ELM-GA中模型中,我们也采用了同样的方式衡量预测的误差。此函数也成为了我们的目标函数,也可以叫做损失函数,我们需要得到它取得最小时的b、W、以及beta参数。Nv即代表了样本值,为了方便大家解读,我把上面公式的符号的解释放在下面,大家好好品味
| 记号 | 表示内容 |
|---|---|
| X | 样本 |
| T | 真实值 |
| f(*) | 激活函数 |
| Nv | 样本数量 |
| N | 隐藏层数量 |
| b | 隐藏层输出时的权重 |
| W | 隐藏层输入时的权重 |
| || || | 范数运算 |
我们已经构建了一个神经网络,并且获得了损失函数,那么我们需要对目标函数进行求解,那么以下就自然引出了遗传算法。
遗传算法
遗传算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
相信大家还记得高中学过的生物。达尔文的进化论告诉了我们适者生存,我来带大家回忆一下,由于个人不是生物专业,如以下观点与生物知识有偏差,请批评指正。
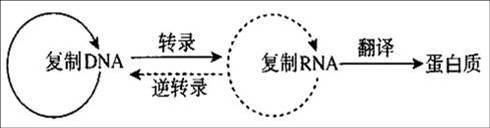
个体携带独一无二的DNA,在细胞内通过转录、翻译等步骤最终形成蛋白质,而不同的蛋白质最终会影响到个体的形状表现,比如肤色,单双眼皮。

在个体之间繁衍后代过程中,子代会得到父母双方一半的染色体数量作为子代个体的遗传代码,在这个过程中也不乏出现一些变异的情况。
个体相对环境而言是微不足道的,只有说个体去适应环境而不能说让环境去适应个体,常言道:改变社会不如改变自己。只有自己去适应环境才能更好的活下去。在遗传过程中也是一样,环境的变化会让一些物种消失,也会让一部分新物种出现,而种群中基因有缺陷的也会很难生存下去。
遗传算法(Genetic Algorithm, GA)正式是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。我们将目标函数当作这个生存的”环境“,将待求解W作为这个物种,使得目标函数值越小的就越容易活下来,反之越容易被淘汰,进而随着一代代的进化,优良的品种会越来越多直到最后充满整个物种数量,最终得到一个收敛的状态,也就是此时,找到那个最优秀的个体,它携带的基因组合所表达的内容就是我们所求解的W。
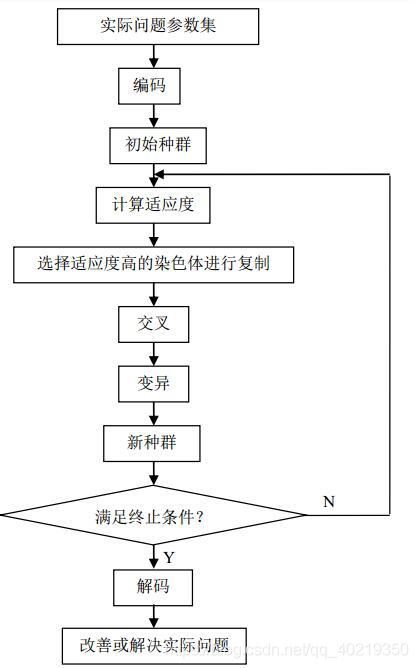
我们思路有了,为了让大家更清晰直观的了解遗传算法的整个过程,接下来放上整个遗传算法的流程图:
三、代码的实现
构建神经网络
- 定义激活函数
def fp(x,p=5):
exp1=4*p-2;exp2=1/(4*p-2)
return x/(0.000001+(1+x**(exp1))**exp2)
- 定义损失函数
#定义神经网络损失函数,输出为目标函数值以及对应的隐藏层偏执向量
#只能对一个个种群单独计算
def function1(W,C=0.1):#含有权重
H_in=X.dot(W)#计算输入隐藏层的数据,因为已经在样本中多添加了参数为1的一列,W也包含了了b的信息,所以H_in代表的是wx+b
H_out=fp(H_in)#在隐藏层中通过激活函数进行映射
HH= H_out.T.dot(H_out); HT = H_out.T.dot(y)
b=np.linalg.pinv(HH+np.identity(W.shape[1])/C).dot(HT)#通过伪逆计算权重beta值(不要和之前的b搞混)
sum2=0
for j in range(X.shape[0]):#通过循环计算残差
sum1=0
for i in range(W.shape[1]):#默认权重从w0常数项开始,包括了偏执b
sum1+=b[i]*fp(W[:,i].dot(X[j]))
error=sum1-y[j]
sum2+=(error)**2
F=np.sqrt(sum2/X.shape[0])#输出损失函数计算的结果
return (F,b)#输出F和b,后期通过列表方式提取
构建遗传算法
- 算法初始化
def __init__(self,objfunction,gen,population_size,hidden,weight,chromosome_length,max_value,death_rate,pc,pm,lower,upper):#定义初始化
self.objfunction=objfunction#目标函数,神经网络,接受的矩阵形式,种群数量*隐藏层*权重分布
self.weight=weight #所求参数的数量
self.population_size=population_size #种群数量
self.hidden=hidden#隐藏层数量
self.cl=chromosome_length#一个参数对应的基因数量
self.choromosome_length=chromosome_length*hidden*weight #基因的长度,单参数基因长度*隐藏层*权重层
self.max_value=max_value#适应度函数参数
self.death_rate=death_rate#自然淘汰率,这个比率代表了有多少种群要被淘汰
self.pc=pc#杂交率
self.pm=pm#变异率
self.gen=gen#迭代率
self.lower=lower#定义参数变量下界
self.upper=upper#定义参数变量上界
- 种群初始化
def species_origin(self):#定义population为种群数量*基因长度的矩阵
population=np.random.randint(0,2,size=(self.population_size,self.choromosome_length))#输出种群数量*基因长度
return population
- 定义DNA翻译函数
def translation(self,population): #定义对一个种群转换为对接神经网络的矩阵,输出为隐藏层*权重分布,
# print(po_ne)
population_3D=population.reshape(self.hidden,self.weight,self.cl)#输出矩阵形式:隐藏层*权重分布*基因向量
population_2D_decimal=np.zeros((self.hidden,self.weight))
for j in range(population_3D.shape[0]):#循环每个隐藏层
for m in range(self.weight):#循环每个权重
total1=0#计算每个权重的大小
for n in range(self.cl):#循环每一位基因进行二进制转十进制
total1+=population_3D[j][m][n]*(math.pow(2,n))
population_2D_decimal[j][m]=total1
for j in range(population_2D_decimal.shape[0]):
for m in range(population_2D_decimal.shape[1]):
population_2D_decimal[j][m]=self.lower+population_2D_decimal[j][m]*(self.upper-self.lower)*self.max_value/(math.pow(2,self.cl)-1)#此处函数为适应函数(不要跟目标函数搞混),分母部分是万年不变的,分子根据所求目标函数进行调整,具体可见[适应度函数](https://wenku.baidu.com/view/d4fd8ab20129bd64783e0912a216147917117e11.html)
return population_2D_decimal
#经过函数转换后,输出了2D形态poputation[i]的十进制表示,population_2D_decimal矩阵的形式为:隐藏层*权重分布
- 定义适应性函数
def fitnessfunc(self,population,fitness):#fitnessfuc计算population的适应能力,返回一维数据,种群数量*1,
for i in range(population.shape[0]):#在此处循环每一个种群
fitness[i]=self.objfunction(self.translation(population[i]).T)[0]#先转换成权重*隐藏层进入神经网络再计算
return (fitness)
- 定义自然选择函数
def selection(self,population,fitness,death_rate):
rat_fitness=np.zeros(fitness.size)#适应度权重初始化
sum_fitness=np.sum(abs(fitness))#适应度求和
for i in range(fitness.size):#在每个种群中迭代
rat_fitness[i]=abs(fitness[i])/sum_fitness#计算每个种群适应度权重
death_idx=np.random.choice(a=population.shape[0], size=math.ceil(death_rate*population.shape[0]),
replace=False, p=rat_fitness)#确定死亡名单,death_idx代表了要删除的序号,权重越高越容易死
new_population=np.delete(population,death_idx,0)#删除死亡名单上的种群
empty_space=population.shape[0]-new_population.shape[0] #计算相比原来种群数量还空缺的位置
for i in range(empty_space):#依次在空缺位置填补,复制原来筛选下来的种群,确保前后数量一致
temp=random.randint(0,new_population.shape[0])-1#随机生成复制目标行的序号
new_population=np.row_stack((new_population,new_population[temp]))#添加复制行
population=new_population#完成自然选择与淘汰
return population
6.定义基因交叉函数
def crossover(self,population):
population_4D=population.reshape(self.population_size,self.hidden,self.weight,self.cl)#输出矩阵形式:种群*隐藏层*权重分布*基因向量
for i in range(population_4D.shape[0]-1):
if(random.random()<self.pc):
for m in range(population_4D.shape[1]):#迭代每一个隐藏层
for n in range(population_4D.shape[2]):#迭代每一个权重层
cpoint=random.randint(0,population_4D.shape[3])#随机找到权重上一个基因位置
temporary1=[]#子代1
temporary2=[]#子代2
temporary1.extend(population_4D[i][m][n][0:cpoint])#在子代1中放入父代1的一段
temporary1.extend(population_4D[i+1][m][n][cpoint:population_4D.shape[3]])#在子代1中放入父代2的一段
temporary2.extend(population_4D[i+1][m][n][0:cpoint])#在子代2中放入父代2的一段
temporary2.extend(population_4D[i][m][n][cpoint:population_4D.shape[3]])#在子代2中放入父代1的一段
population_4D[i][m][n]=np.asarray(temporary1)
population_4D[i+1][m][n]=np.asarray(temporary2)#完成染色体交换
population_4D.reshape(self.population_size,self.choromosome_length)
return population
7.定义基因变异函数
def mutation(self,population):
px=population.shape[0]
py=population.shape[1]
for i in range(px):#在种群中迭代
if(random.random()<self.pm):#随机生成一个数和变异率比较,如果比变异率还小的话进行以下操作
for j in range(self.weight*self.hidden):#g根据基因的长短进行变异的次数
mpoint=random.randint(0,py-1)#在基因的某个位置生成一个变异点
if(population[i][mpoint]==1):#进行1到0的变换或0到1的变换
population[i][mpoint]=0
else:
population[i][mpoint]=1
return population
- 定义选择最优个体的函数
def best(self,population,fitness,best_individual,best_fitness):
px=population.shape[0]
best_fitness=fitness[0] #先定义bestfitness作对比
for i in range(1,px):
if fitness[i]<best_fitness: #同时满足适应度>0并且要比目前最好的还要好
best_fitness=fitness[i]#更新最优秀的适应度
best_individual=population[i]#更新最优秀的基因
return (best_individual,best_fitness)
9.定义主函数
def main(self):
fitness=np.zeros(self.population_size)#随机初始化适应度,初始化
population = self.species_origin()#初始化种群,初始化
fitness=self.fitnessfunc(population,fitness)#更新初始化适应度以及隐藏层偏执
best_b=np.zeros(population.shape[1])#创建最佳隐藏层偏执列表,初始化
best_individual=np.random.randint(0,2,self.choromosome_length)#存储最优秀的种群基因,初始化
best_hidden_weight=np.zeros((self.hidden,self.weight))#存储最优秀的2D性状,隐藏层*权重分布,初始化
best_fitness=10000000#存储最优秀个体的适应度
best_fitness_note=np.zeros(self.gen)#记录每一次迭代的最优秀个体适应度
print('====================物种初始化结束,开始进化=====================')
for i in tqdm(range(self.gen)):
population=self.selection(population,fitness,self.death_rate)#进行自然选择淘汰
population=self.crossover(population)#进行基因杂交
population=self.mutation(population)#进行基因突变
fitness=self.fitnessfunc(population,fitness)#更新初始化适应度以及隐藏层偏执
best_individual,best_fitness=self.best(population,fitness,best_individual,best_fitness)#寻找最佳
best_hidden_weight=self.translation(best_individual)#更新最优秀的2D性状,隐藏层*权重分布
best_fitness_note[i]=best_fitness#记录最优适应度记录
if i%10==0:#此方法非模型部分,是为了方便查看每10次迭代后的效果
best_b=self.objfunction(best_hidden_weight.T)[1]
predict=predict1(best_hidden_weight.T,best_b)
for i in range(predict.size):
if predict[i]>0:
predict[i]=1
else:
predict[i]=-1
sum=0
for i in range(predict.size):
if predict[i]==y_test[i]:
sum+=1
rate=sum/len(predict)
print('预测成功率:',rate)
print('目前轮次中最好的适应度是:',best_fitness)
print('========================继续进化=========================')
best_individual,best_fitness=self.best(population,fitness,best_individual,best_fitness)#更新最优秀的适应度和基因
best_fitness_note[-1]=best_fitness#记录最优适应度记录
best_hidden_weight=self.translation(best_individual).T#更新最优秀的2D性状,隐藏层*权重分布
best_b=self.objfunction(best_hidden_weight)[1]#更新最优秀的隐藏层偏执
print('最好的隐藏层矩阵是:',best_hidden_weight)
print('最好的隐藏层偏执是:',best_b)
print('最好的适应度是:',best_fitness)
plt.plot(best_fitness_note)
print('最终预测成功率:',rate)
print('=========================END=======================')
return (best_hidden_weight,best_b)
调控程序
#澳大利亚数据集,参数为15个(含常数项)
data = np.loadtxt(r'dataset/australian.dat')#这是我自己的文件位置
ss = StandardScaler()
ones=np.ones(data.shape[0])#增加一列,方把常数项b带入到矩阵计算
data = np.column_stack((ones,data))
for i in range(data.shape[0]):#根据激活函数特性,把标签列的0改成-1
if data[:,-1][i]==0:
data[:,-1][i]=-1
#我们取后650个数据作为训练集,剩下部分作为测试集
X_test=data[-650:,:-1]
y_test=data[-650:, -1]
X=data[:-650,:-1]
y=data[:-650:, -1]
X=ss.fit_transform(X)#训练集标准化
X_test=ss.fit_transform(X_test)#测试集标准化
# (self,population_size,hidden,weight,chromosome_length,max_value,pc,pm):
ga=GA(objfunction=function1,gen=10,population_size=100,hidden=6,weight=15,chromosome_length=10,
max_value=10,death_rate=0.75,pc=0.75,pm=0.02,lower=-4,upper=4)
W,b=ga.main()
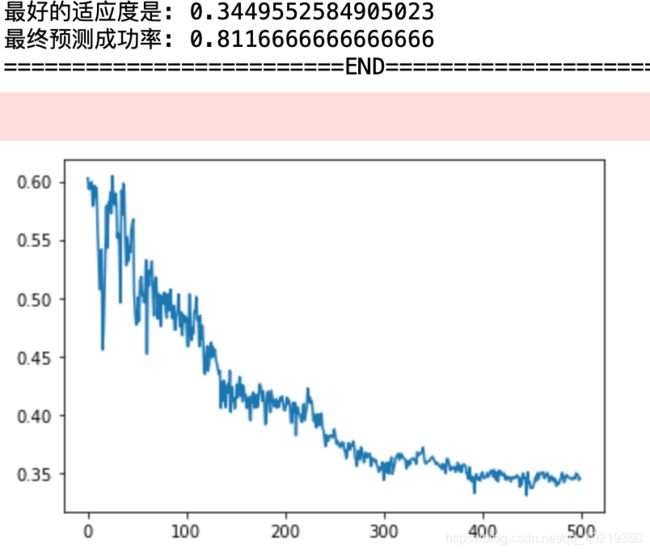
ELM-GA模型二分类及优化GA模型效果展示
上述图片反应了适应度的变化。由于计算量较大,整个运算花了近43分钟,仅迭代了500次,也可能是电脑性能不足吧。虽然在迭代500次后,最佳适应度还有继续优化的趋向,但是预测成功率在第一次就已经上到了80%以上。为了证明模型稳定性,我对于不同的样本段进行测试,预测准确度也在前几次就上了80%,说明了此模型对于机器学习中二分类的问题具有迭代次数少,精度高的优势。
2.房价样本集
为了测试多维框度架下的优化遗传算法的回归能力,我对自己的另一个数据集进行了预测,由于参数需要14位,我将隐藏层设置2层,权重层设置7层,最后预测的时候把矩阵平铺代入预测,样本数据如下:
#房价数据集,参数为14个(含常数项)
data = pd.read_csv(r"dataset/boston.csv")
new_columns = data.columns.insert(0, "Intercept")
t= data.reindex(columns=new_columns, fill_value=1)
t=pd.DataFrame.drop(t,columns='Unnamed: 0')
ss = StandardScaler()
t=ss.fit_transform(t)
#训练集前400个,剩余编测试集
X=t[:400,:-1]
y=t[:400, -1]
X_test=t[400:,:-1]
y_test=t[400:, -1]
得到的适应性变化如下:
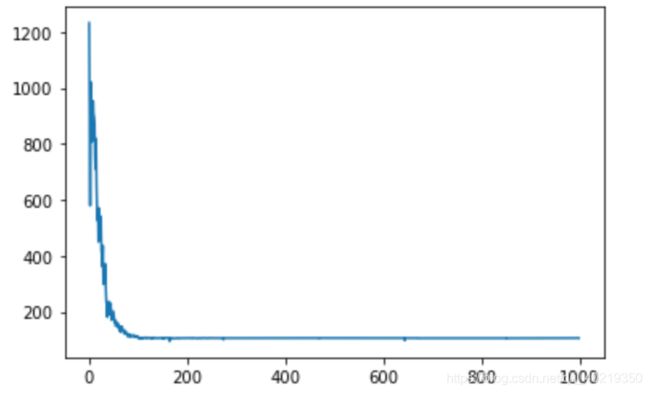
我们可以看到,适应性在100代左右就已经收敛,我们来看一下预测精度:
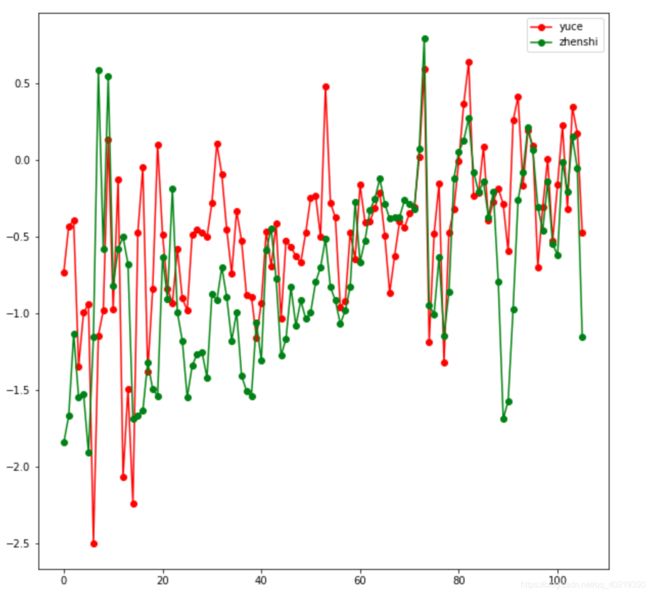
从最后预测的结果来看,效果也还说得过去,但是遗传算法的回归性能跟遗传算法运用在ELM二分类上的性能相比,还是有点不足。
四、总结与展望
本模型的不足之处
ELM与GA的组合在二分类的实测中达到了迭代次数少,精度高,但是依然不能和主流的决策树、KNN、SVM等算法相提并论,毕竟代码原创,封装度不高,不能完全适应所有的实践情况,就像机械一样,越复杂的机械故障率也就越高,维护时间和修改代码也较为繁琐。此模型并不一定能作为主流,但是也能给广大的决策者提供一定的参考和对比价值。
致谢与参考文献
- Diwakar Tripathi,Evolutionary Extreme Learning Machine with novel activation function for credit scoringEngineering[J],Applications of Artificial Intelligence,2020(96)
- 《Python最优化算法实战》225-233
- 博主quinn1994
五、附录:完整代码
ELM
#定义激活函数,函数暂定
def fp(x,p=5):
exp1=4*p-2;exp2=1/(4*p-2)
return x/(0.000001+(1+x**(exp1))**exp2)
#定义神经网络损失函数,输出为目标函数值以及对应的隐藏层偏执向量
def function1(W,C=0.1):
H_in=X.dot(W)
H_out=fp(H_in)
HH= H_out.T.dot(H_out); HT = H_out.T.dot(y)
b=np.linalg.pinv(HH+np.identity(W.shape[1])/C).dot(HT)
sum2=0
for j in range(X.shape[0]):
sum1=0
for i in range(W.shape[1]):
sum1+=b[i]*fp(W[:,i].dot(X[j]))
error=sum1-y[j]
sum2+=(error)**2
F=np.sqrt(sum2/X.shape[0])
return (F,b)
#用于function1的预测函数
def predict1(W,b,C=0.1):
H_in=X_test.dot(W)
fx=H_in.dot(b)
return fx
GA
class GA:
def __init__(self,objfunction,gen,population_size,hidden,weight,chromosome_length,max_value,death_rate,pc,pm,lower,upper):#定义初始化
self.objfunction=objfunction
self.weight=weight
self.population_size=population_size
self.hidden=hidden
self.cl=chromosome_length
self.choromosome_length=chromosome_length*hidden*weight
self.max_value=max_value
self.death_rate=death_rate
self.pc=pc
self.pm=pm
self.gen=gen
self.lower=lower
self.upper=upper
def species_origin(self):
population=np.random.randint(0,2,size=(self.population_size,self.choromosome_length))
return population
def translation(self,population):
population_3D=population.reshape(self.hidden,self.weight,self.cl)
population_2D_decimal=np.zeros((self.hidden,self.weight))
for j in range(population_3D.shape[0]):
for m in range(self.weight):
total1=0
for n in range(self.cl):
total1+=population_3D[j][m][n]*(math.pow(2,n))
population_2D_decimal[j][m]=total1
for j in range(population_2D_decimal.shape[0]):
for m in range(population_2D_decimal.shape[1]):
population_2D_decimal[j][m]=self.lower+population_2D_decimal[j][m]*(self.upper-self.lower)*self.max_value/(math.pow(2,self.cl)-1)
return population_2D_decimal
def fitnessfunc(self,population,fitness):
for i in range(population.shape[0]):
fitness[i]=self.objfunction(self.translation(population[i]).T)[0]
return (fitness)
def selection(self,population,fitness,death_rate):
rat_fitness=np.zeros(fitness.size)
sum_fitness=np.sum(abs(fitness))
for i in range(fitness.size):
rat_fitness[i]=abs(fitness[i])/sum_fitness
death_idx=np.random.choice(a=population.shape[0], size=math.ceil(death_rate*population.shape[0]),
replace=False, p=rat_fitness)
new_population=np.delete(population,death_idx,0)
empty_space=population.shape[0]-new_population.shape[0]
for i in range(empty_space):
temp=random.randint(0,new_population.shape[0])-1
new_population=np.row_stack((new_population,new_population[temp]))
population=new_population
return population
def crossover(self,population):
population_4D=population.reshape(self.population_size,self.hidden,self.weight,self.cl)
if(random.random()<self.pc):
for m in range(population_4D.shape[1]):
for n in range(population_4D.shape[2]):
cpoint=random.randint(0,population_4D.shape[3])
temporary1=[]#子代1
temporary2=[]#子代2
temporary1.extend(population_4D[i][m][n][0:cpoint])
temporary1.extend(population_4D[i+1][m][n][cpoint:population_4D.shape[3]])
temporary2.extend(population_4D[i+1][m][n][0:cpoint])
temporary2.extend(population_4D[i][m][n][cpoint:population_4D.shape[3]])
population_4D[i][m][n]=np.asarray(temporary1)
population_4D[i+1][m][n]=np.asarray(temporary2)
population_4D.reshape(self.population_size,self.choromosome_length)
return population
def mutation(self,population):
px=population.shape[0]
py=population.shape[1]
for i in range(px):
if(random.random()<self.pm):
for j in range(self.weight*self.hidden):
mpoint=random.randint(0,py-1)
if(population[i][mpoint]==1):
population[i][mpoint]=0
else:
population[i][mpoint]=1
return population
def best(self,population,fitness,best_individual,best_fitness):
px=population.shape[0]
best_fitness=fitness[0]
for i in range(1,px):
if fitness[i]<best_fitness:
best_fitness=fitness[i]
best_individual=population[i]
return (best_individual,best_fitness)
def main(self):
fitness=np.zeros(self.population_size)
population = self.species_origin()
fitness=self.fitnessfunc(population,fitness)
best_b=np.zeros(population.shape[1])
best_individual=np.random.randint(0,2,self.choromosome_length)
best_hidden_weight=np.zeros((self.hidden,self.weight))
best_fitness=10000000
best_fitness_note=np.zeros(self.gen)
print('====================物种初始化结束,开始进化=====================')
for i in tqdm(range(self.gen)):
population=self.selection(population,fitness,self.death_rate)
population=self.crossover(population)
population=self.mutation(population)
fitness=self.fitnessfunc(population,fitness)
best_individual,best_fitness=self.best(population,fitness,best_individual,best_fitness)
best_hidden_weight=self.translation(best_individual)
best_fitness_note[i]=best_fitness
if i%10==0:
print('预测成功率:',rate)
print('目前轮次中最好的适应度是:',best_fitness)
print('========================继续进化=========================')
best_individual,best_fitness=self.best(population,fitness,best_individual,best_fitness)
best_fitness_note[-1]=best_fitness#记录最优适应度记录
best_hidden_weight=self.translation(best_individual).T
best_b=self.objfunction(best_hidden_weight)[1]
print('最好的隐藏层矩阵是:',best_hidden_weight)
print('最好的隐藏层偏执是:',best_b)
print('最好的适应度是:',best_fitness)
plt.plot(best_fitness_note)
print('最终预测成功率:',rate)
print('=========================END=======================')
return (best_hidden_weight,best_b)