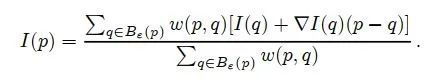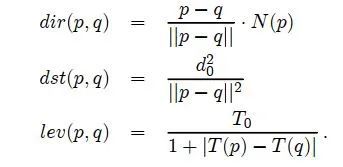【手撕算法】FMM图像修复算法C++实现
FMM算法出自Telea的论文
An Image Inpainting Technique Based on the Fast Marching Method
opencv的inpaint函数就是采用了Telea的基于FMM的图像修复算法,本文基于opencv的inpaint函数,该函数源码位于(我的):
opencv\sources\modules\photo\src\inpaint.cpp
FMM算法基于的思想是,先处理待修复区域边缘上的像素点,然后层层向内推进,直到修复完所有的像素点。
下面以灰度图为例,我们只需要计算出像素新的灰度值即可。对于彩色图像,分别用同样的方法处理各个通道即可。
算法原理
修复一个像素:
首先还是先看下论文中的一个图:
![]()
以修复当前像素点为例。
Ω区域是待修复的区域;δΩ指Ω的边界;要修复Ω中的像素,就需要计算出新的像素值来代替原值。
现在假设p点是我们要修复的像素。以p为中心选取一个小邻域B(ε),该邻域中的点像素值都是已知的(只要已知的)。(这个ε就是opencv函数中参数 inpaintRadius)
q为 Bε(p)中的一点,由q点计算P的灰度值公式如下:
显然,我们需要的是用邻域Bε(p)中的所有点计算p点的新灰度值。显然,各个像素点所起的作用应该是不同的,也就引入了权值函数来决定哪些像素的值对新像素值影响更大,哪些比较小。采用下面的公式:
这里的w(p, q)就是权值函数,是用来限定邻域中各像素的贡献大小的。
w(p, q) = dir(p, q) · dst(p, q) · lev(p, q)
其中,d0和T0分别为距离参数和水平集参数,一般都取为 1。
方向因子 dir(p,q)保证了越靠近法线方向 N=∇T的像素点对 p 点的贡献最大;几何距离因子 dst(p,q)保证了离 p 点越近的像素点对p 点贡献越大;水平集距离因子lev(p,q)保证了离经过点 p 的待修复区域的轮廓线越近的已知像素点对点 p 的贡献越大。
修复的顺序:
考虑是什么样的顺序来处理待修复区域中的所有像素。作者采用的是快速行进方法Fast Marching Method(FMM)。
行进算法伪代码:
δΩi = boundary of region to inpaint//修复区域的边缘
δΩ = δΩi
while (δΩ not empty)
{
p = pixel of δΩ closest to δΩi//修复距离边缘最近的像素
inpaint p using Eqn.2//利用公式2修复p点
advance δΩ into Ω//把边缘向里行进
}
可以看到,修复的顺序是按照当前像素距离边缘的距离进行确定的,那如何计算距离呢?
算法中为待修复区域边缘构建了一个窄边(narrowBand),就是上面所说的δΩ。在opencv里是利用先将mask膨胀得到mask2(结构元素是长为2*ε+1的十字形,以中心点为原点),再用mask2减去mask得到band图,则band中非0元素即narrowBand。
从这里可以看出最初的narrowBand(即δΩ1)是不需要修复的。确定窄边的目的就是为了找到下面要修复的像素。
首先将像素分为三类,用flag标识记录:
BAND:其实就是δΩ上的像素;
KNOWN:就是δΩ外部不需要修复的像素;
INSIDE:就是δΩ内部的等待修复的像素
另外,每个像素还需要存储两个值:T(该像素离到边缘 δΩ的距离);I(灰度值)
下面先说一下处理像素是按怎样的行进方式的:
-
初始化 首先按上面说的方法找到narrowBand,flag记为BAND;窄边内部的待修复区域记为INSIDE,已知像素flag设为KNOWN。
BAND和KNOWN类型的像素T值初始化为0,INSIDE类型像素T值设为无限大(实际中设为106)。
-
定义一个数据结构NarrowBand(opencv中采用双向链表实现),将窄边中的像素按T值升序排列,依次加入到NarrowBand中,先处理T最小的像素。
假设为p点,将p点类型改为KNOWN,然后依次处理p点的四邻域点Pi。
如果Pi类型为INSIDE,则重新计算,修复该点,并更新其T值,修改该点类型为BAND,加入到NarrowBand中(这里仍按顺序,即始终保持NarrowBand是按升序排列的)。
依次进行,每次处理的都是NarrowBand中T最小的像素,直到NarrowBand中没有像素。
伪代码如下:
while (NarrowBand not empty)
{
extract P(i,j) = head(NarrowBand); /* STEP 1 *//*提取T值最小像素*/
for (k,l) in (i-1,j),(i,j-1),(i+1,j),(i,j+1)/*依次处理该像素的四邻域像素*/
{
if (f(k,l)!=KNOWN)
{
if (f(k,l)==INSIDE)
{
f(k,l)=BAND; /* STEP 2修改(k,l)像素点的lag*/
inpaint(k,l); /* STEP 3修复(k,l)像素点*/
}
T (k,l) = min(solve(k-1,l,k,l-1), /* STEP 4 更新(k,l)像素点的值*/
solve(k+1,l,k,l-1),
solve(k-1,l,k,l+1),
solve(k+1,l,k,l+1));
insert(k,l) in NarrowBand; /* STEP 5 将(k,l)像素点加入NarrowBand*/
}
}
}
执行opencv的inpaint函数:
int main()
{
std::chrono::steady_clock clk;
auto begin = clk.now();//开始计时
Mat srcImage, dstImage, mask;
srcImage = imread("image/image3.jpg");
mask = imread("image/mask3.jpg", 0);
if (mask.empty() || srcImage.empty())
{
printf_s("图片读取失败");
return -1;
}
inpaint(srcImage, mask, dstImage, 3, INPAINT_TELEA);
imshow("src", srcImage);
imshow("mask", mask);
imshow("dst", dstImage);
auto time = std::chrono::duration_cast (clk.now() - begin);
std::cerr << "time : " << time.count() << std::endl;
waitKey();
return 0;
}
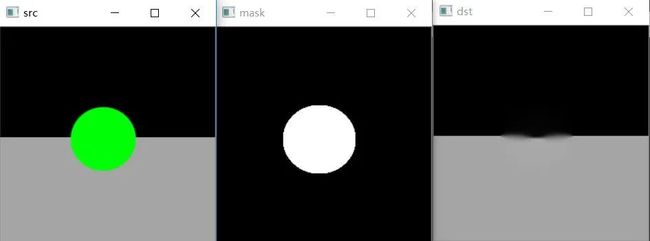
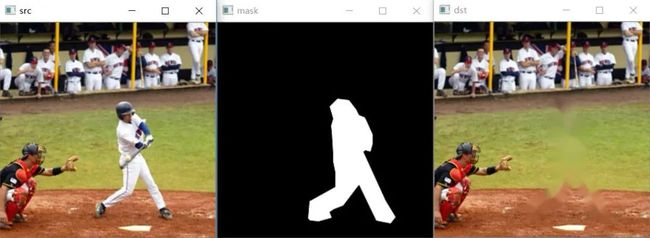
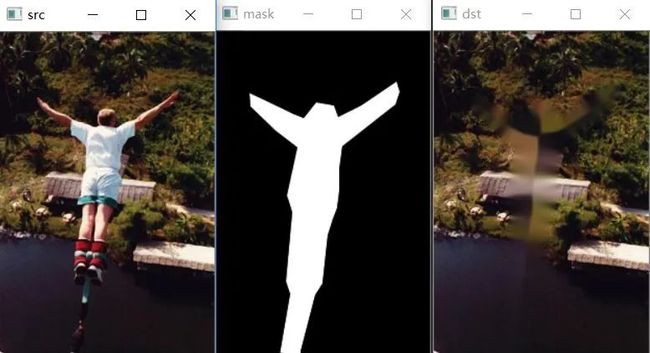
算法效果
可以看到,修复越进行到内部,则越模糊,因为该算法是推进式的,而不是块匹配式的。
但该算法在修复偏窄长的划痕时效果会非常好,不适用于这种大块的填充。
对这个FMM算法我并没能理解的很细节,导致我没能把代码写出来,只能跑opencv的inpaint函数了,大家自己有兴趣可以参看着之前发的综述整理里的文章自己复现一下。
THE END
今天就到这里啦,微信搜索【Opencv视觉实践】,对【计算机视觉/机器视觉算法和软件开发】感兴趣的小伙伴可以一起来学习呀。
关注后 后台回复
【电子书资源】可以领取10G计算机视觉/软件开发相关电子书
【手撕算法代码】可以领取手撕算法系列专栏的所有代码和PDF版论文
【加群】可以加入我们的视觉算法靓仔群~